喷杆喷雾机旋翼悬浮式喷杆自动调平控制系统研究

周志艳 周铭杰 陈羽立 明 锐 向 颖 罗锡文

(1.华南农业大学工程学院， 广州 510642； 2.华南农业大学广东省农业人工智能重点实验室， 广州 510642；3.岭南现代农业科学与技术广东省实验室， 广州 510642；4.广东省农业航空应用工程技术研究中心， 广州 510642；5.闽江学院福建省信息处理与智能控制重点实验室， 福州 350108；6.华南农业大学南方农业机械与装备关键技术教育部重点实验室， 广州 510642)

0 引言

喷杆喷雾机是大田植保作业的主要机具之一。常见的喷杆喷雾机作业幅宽通常为12 m左右，随着农机化水平的提高，对高效率、智能化植保机械的需求不断增大[1]，增加喷杆长度提升作业幅宽是提高作业效率的主要手段。现有喷杆喷雾机的喷杆大多采用传统桁架结构，但随着喷杆长度的增加，配套机构、设计复杂度及整机质量也相应增加[2-3]。

国内外现有的大型喷杆喷雾机最大作业幅宽可达44 m[4]，单机总质量达10 t左右，整机质量大，农田中行走的通过性差，陷车风险高，且能耗及压苗损失随之加大，作业成本上升；农田泥底层高低不平，喷杆易产生摆动，平衡控制难度加大，降低了整机的可靠性和便利性[5-7]。特别是在小行距的作物(如水稻)喷施作业中，大型喷杆喷雾机的功能受到很大限制[8]。

为进一步提升大型喷杆喷雾机的性能，国内外学者进行了大量的研究。韩红阳等[9]采用尺寸优化法对机动式喷杆喷雾机机架进行了轻量化研究，使用优化设计软件Optistruct对机架进行轻量化设计，但尚未见实际应用试验的报道；陈晨等[10]针对喷雾机喷杆结构动力学原始设计缺陷，提出了一种基于遗传算法的多变量优化方法来优化喷杆结构，但该结构在质量减轻的同时使得竖直方向上的振动位移响应量增大；TUDOSE等[11]通过提出的一种系统进化算法得到喷杆的最优几何结构模型，在满足要求的情况下减轻了喷杆质量，但尚未见在生产中进行验证试验和应用的报道。针对喷杆钟摆式主被动悬架系统存在的参数不确定性和控制精度低、稳定性差等问题，国内外一些研究人员开展了基于模型补偿的自适应鲁棒控制器的研究，提高了喷杆系统稳定性[12-13]；针对喷杆的振动问题，部分学者采用PID控制和模糊PID控制液压系统对喷杆进行主动抑振，但在实际应用中效果仍不理想[14-15]；ANTHONIS等[16]对约翰迪尔喷雾机的双摆垂直悬挂系统进行了优化设计，通过最小化的目标函数得到最优阻尼器，但可靠性有待进一步验证。综上，目前的研究主要通过控制算法抑制喷杆振动以及优化桁架结构来提升整机性能，但由于桁架结构空间大、侧向刚度小等特点，当作业幅宽增加时，其固有的缺陷依然较难克服。

近年来，由于植保无人机具有体型小、作业灵活、地形地貌的限制少等特点，发展迅速，但植保无人机的续航和药液搭载能力有限，决定了无人机植保作业必须采用超低容量喷雾法，存在雾滴细易飘移、穿透力不够、雾滴沉积效果不够好等问题，是植保无人机飞防中难以攻克的问题。

针对上述问题，提出一种旋翼悬浮式喷杆(简称喷杆)作业方法，在喷杆上安装多个旋翼为喷杆提供升力，分别融合地面机械高续航、载重大和空中无人机作业灵活、受地形地貌限制小的优点，可简化复杂臃肿的桁架结构，减轻机体的整体自重，同时，旋翼下压风场能减小雾滴飘移造成的二次污染。为验证方案的可行性，采用“陀螺仪+激光雷达”进行双传感器融合控制的方式，开展旋翼悬浮式喷杆自动调平控制系统设计与试验，以期为旋翼悬浮式喷杆喷雾机的样机研制提供参考。

1 旋翼悬浮式喷杆工作原理

1.1 旋翼悬浮式喷杆喷雾机整机结构

旋翼悬浮式喷杆喷雾机结构简图如图1所示，主要包括转向舵机、电源、驱动电机、药液箱、药液雾化系统、整机主控系统、自动调平控制系统、协同控制系统等。

图1 旋翼悬浮式喷杆喷雾机结构示意图Fig.1 Structure diagram of rotors hovering spray boom sprayer1.转向舵机 2.电源 3.驱动电机 4.药液箱 5.药液雾化系统 6.整机主控系统 7.自动调平控制系统 8.陀螺仪1 9.激光雷达1 10.陀螺仪2 11.陀螺仪3 12.陀螺仪4 13.激光雷达2 14.协同控制系统 15.陀螺仪5

在喷雾机作业过程中，自动调平控制系统根据传感器检测的数据，实现喷杆自动调平。同时，车身向前运动，安装在喷杆上的协同控制系统与车身协同前进，从而带动喷杆一同向前运动。

1.2 自动调平控制系统组成及原理

喷杆自动调平控制系统主要由智能锂电池(14 s欧荷牌，标称电压51.8 V)、控制器(处理器为STM32F103RCT6)、陀螺仪(MPU6050，深圳维特智能科技有限公司)、激光雷达(TFmini Plus，北醒光子科技有限公司)、无刷直流电机(枭鹰EA60-170KV型，中山枭鹰动力科技有限公司)、电调(枭鹰EP-80A型，中山枭鹰动力科技有限公司)及旋翼(T2055型,中山枭鹰动力科技有限公司)等组成，喷杆通过方管铰接件与车身连接，如图2所示。方管铰接件分为左、右两个零部件，通过螺栓连接，使喷杆仅有一个绕x轴的转动副。左边的零部件通过螺栓固定在喷雾机车身上，右边的零部件与方管过盈配合，通过两侧的夹紧装置将方管夹紧。

图2 方管铰接件Fig.2 Square pipe hinge

自动调平控制系统的工作原理如图3所示，主要为：当旋翼悬浮式喷杆喷雾机在作业过程中发生车身倾斜时，喷杆与水平面之间的夹角会发生改变，同时喷杆距离作物冠层的高度也发生改变；安装在喷杆上的陀螺仪和激光雷达将测量到的数据发送给控制器，通过角度偏差和高度偏差，利用模糊控制算法融合相应位置的角度PID和高度PID输出量，调整PWM(Pulse width modulation)信号占空比，进而控制无刷直流电机转速，带动旋翼产生使喷杆达到目标悬浮状态所需要的升力；当角度偏差和高度偏差均为零时，旋翼所提供的升力与喷杆自身重力大小相等，方向相反，此时整根喷杆保持水平，平行于作物冠层，实现喷杆自动调平。

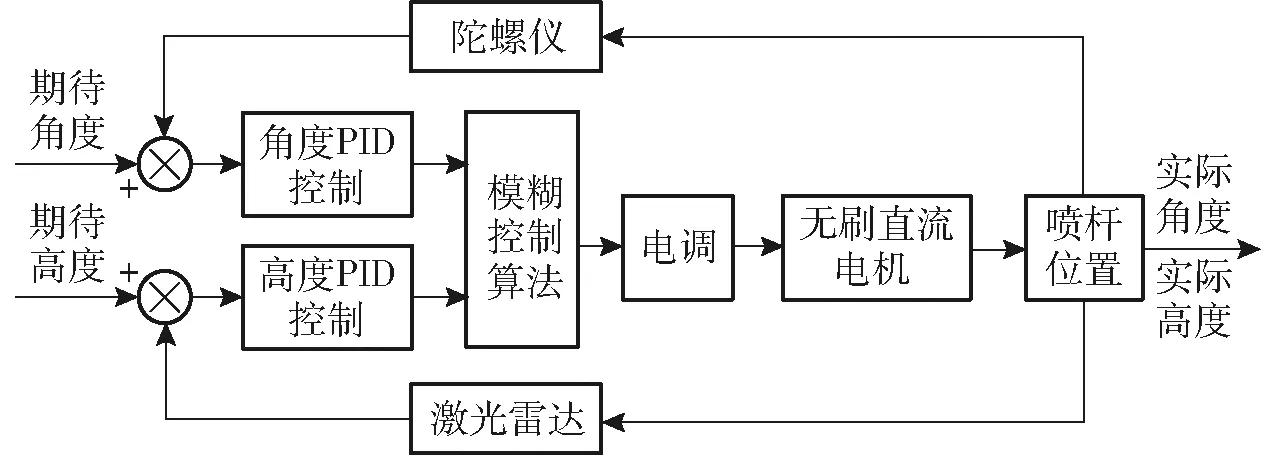
图3 自动调平控制系统原理图Fig.3 Schematic of automatic leveling control system

1.3 旋翼悬浮式喷杆受力分析

喷杆由若干碳纤维方管(简称方管)、连接件、电机座、无刷直流电机、桨叶等组成。喷杆整体结构由10节2 m的方管组成，方管之间通过连接件连接；每个电机和桨叶通过电机座分别安装在各节方管的中点位置。相邻旋翼转动方向相反，当转速相同时，保证旋翼的反扭力两两相互抵消[17]，使喷杆不会绕z轴旋转。相邻方管的力矩分析图如图4所示。其中O为车身与第一节方管铰接处，A为第1、2节方管的连接处；M1、M2分别为第1、2节方管所受力矩。

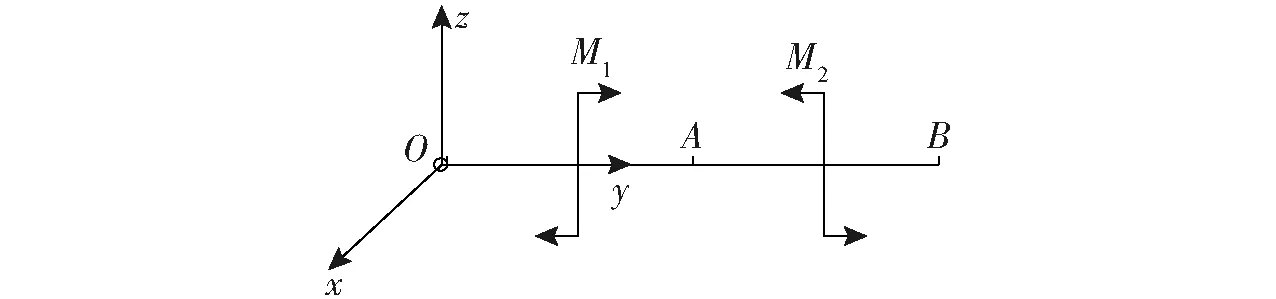
图4 相邻方管的力矩分析图Fig.4 Torque analysis diagram of adjacent square tubes

喷杆的受力分析图可简化为图5。其中B、D、F、H分别为第2和3、4和5、6和7、8和9节方管的连接处，J为喷杆端部；F1、F2、F3、F4、F5分别为第1和2、3和4、5和6、7和8、9和10号方管旋翼升力的合力。

在工作过程中，由于受到地面的随机干扰，容易使喷杆产生惯性，喷杆转动惯量与惯性力的计算公式为

(1)

(2)

式中Jω——转动惯量，kg·m2

Fλ——惯性力，N

m——喷杆质量，kg

l——喷杆长度，m

a——角加速度，rad/s2

根据试验测试得到作业喷杆长度、质量、角加速度，代入式(1)、(2)可得转动惯量为404.3 kg·m2，惯性力为11.4 N，属于闭环控制的调节范围，可根据传感器数据变化调节电机转速，实现喷杆再次调平。因此，在分析闭环控制的过程中，可以忽略由地面不平产生的随机扰动带来的影响。

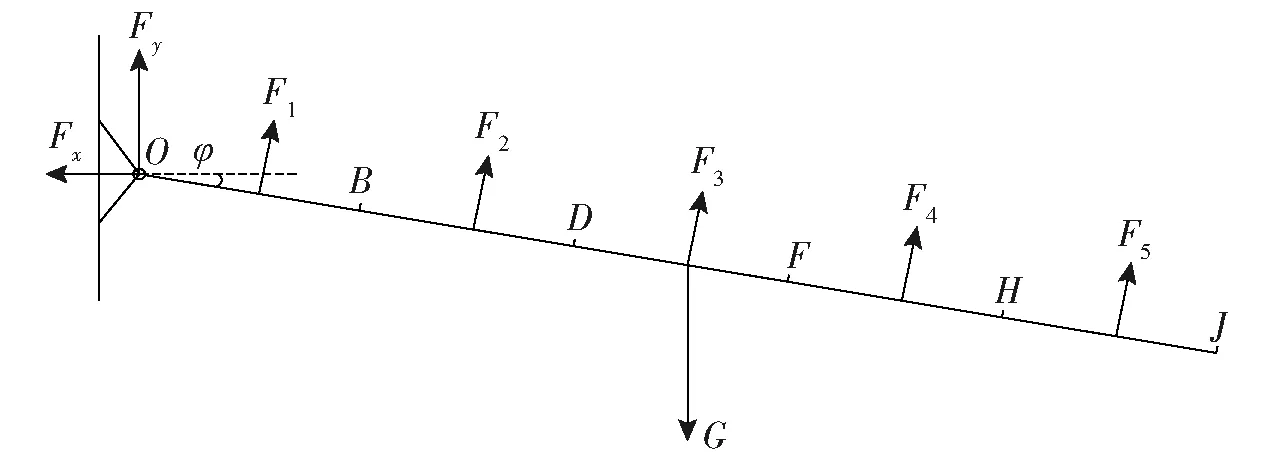
图5 喷杆受力分析图Fig.5 Spray boom force analysis diagram

由图5可知

(F1+F2+F3+F4+F5)sinφ-Fx=0

(3)

(F1+F2+F3+F4+F5)cosφ+Fy-G=0

(4)

(5)

式中F1——第1和2号方管旋翼升力的合力，N

F2——第3和4号方管旋翼升力的合力，N

F3——第5和6号方管旋翼升力的合力，N

F4——第7和8号方管旋翼升力的合力，N

F5——第9和10号方管旋翼升力的合力，N

Fx——车身对喷杆的横向力，N

Fy——车身对喷杆的轴向力，N

G——喷杆所受重力，N

φ——喷杆与水平面夹角，(°)

λ——相邻两节方管长度，m

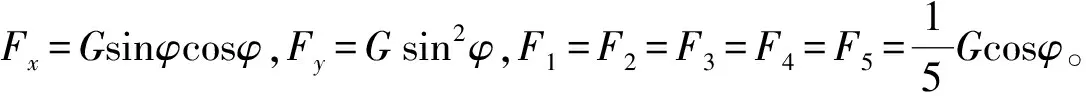
2 自动调平控制系统辨识与建模

2.1 无刷直流电机电机模型

本文采用枭鹰EA60-170KV型无刷直流电机，根据基尔霍夫定律[18]可得电枢回路方程为

(6)

其中

ea=Ken

(7)

式中ua——电枢两端的输入电压，V

ia——电枢绕组电流，A

ea——电机反电动势，V

L——电枢绕组电感，H

Ra——电枢绕组电阻，Ω

Ke——电机反电动势系数

n——电机轴转速，r/s

为构建电机系统的完整数学模型，除了电压方程，还需引入转矩方程和电机运动方程

(8)

其中

Te=KTia

(9)

式中J——转子转动惯量，kg·m2

Te——电磁转矩，N·m

TL——负载转矩，N·m

KT——电机转矩系数

Bv——黏滞摩擦系数

由于枭鹰EA60-170KV型无刷直流电机为小型电机，可以忽略黏滞摩擦系数Bv的影响。对式(6)、(8)作拉氏变换可得

(10)

(11)

本文采用PWM信号调节电枢电压ua，根据文献[19-20]可知，忽略电路的延时，PWM变换器可简化为

ua=dKa

(12)

式中d——PWM信号占空比

Ka——PWM信号占空比与电枢电压转换系数

由式(7)、(9)、(11)、(12)可形成一个带负反馈的闭环二阶控制系统，联立得出电机转速和PWM信号占空比的传递函数为

(13)

通过多组试验测得电机转速n与喷杆角度θ以及喷杆距冠层高度h之间的关系，同时测得PWM信号占空比与电枢电压转换系数Ka；根据电机数据手册，得到该型号电机的相关参数[21-23]，代入式(13)可得PWM信号占空比与喷杆角度θ和喷杆距冠层高度h的传递函数分别为

(14)

(15)

2.2 单传感器PID控制算法

传统的PID控制算法包括位置式和增量式两种，本文采用增量式PID算法，即数字控制器的输出由控制器的增量Δuk组成，离散的PID表达式为

(16)

(17)

(18)

式中dk——第k次采样时间输出的PWM信号占空比

Kp——比例系数

Ki——积分系数

Kd——微分系数

ek——第k次采样偏差

T——采样时间，s

Ti——积分时间常数

Td——微分时间常数

由式(16)递推得增量式PID控制算法公式为

Δuk=uk-uk-1=

(19)

2.3 双传感器融合的模糊PID控制算法

由于旋翼悬浮式喷杆较长，工况较为复杂，不确定性较大，单一传感器PID控制较难满足响应速度、控制精度、抗干扰能力的要求。因此，利用模糊控制算法融合角度PID和高度PID的数据进行协调控制。模糊控制系统的核心是模糊控制器[24-25]。以喷杆距冠层的高度偏差E和角度偏差变化率EC作为输入，高度PID和角度PID的权重比系数Q作为输出。根据喷杆自动调平过程中激光雷达和陀螺仪输出的数据可知，喷杆距冠层的高度偏差为-0.3～0.3 m，角度偏差变化率为-0.15～0.15(°)/s。因此，设高度偏差E和角度偏差变化率EC的基本论域分别为[-0.3,0.3]m和[-0.15,0.15](°)/s；输出量Q的基本论域为[0，1]。假设输入和输出对应的论域都是[-0.3，0.3]，则高度偏差E和角度偏差变化率EC的量化因子分别为KE=1、KEC=2；输出量Q的量化因子为KQ=0.6。模糊规则的模糊子集为{NB,NM,NS,ZE,PS,PM,PB},分别表示负大、负中、负小、零、正小、正中、正大；输入输出的隶属度函数都采用三角形函数。根据模糊规则的一般设计原则[26-28]以及大量的试验，得到Q的模糊控制规则如表1所示。本文模糊控制器去模糊化采用重心法[29]，通过各自的比例因子即可在线自整定权重比系数Q，从而调整PWM信号占空比来控制电机转速，实现喷杆快速达到平衡。

3 试验

3.1 试验方法

3.1.1仿真试验

在Matlab/Simulink模块中建立仿真模型，整定PID控制最优参数，得到仿真响应曲线如图6所示，图中tr为上升时间，ts为进入稳态的调节时间(由于喷杆较长，调试过程中各组PID控制之间相互产生干涉。因此，ts指从电机上电开始工作到喷杆相关的各被控制量的稳态误差在±10%以内所用时间[30])，Mp为超调量；同时建立模糊控制规则表，验证模糊控制算法融合两种传感器数据的有效性。

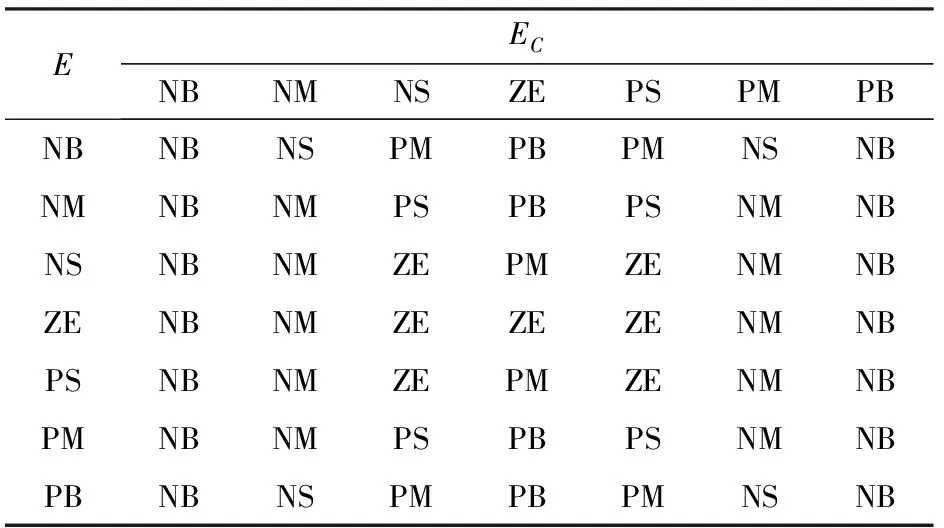
表1 模糊控制规则Tab.1 Fuzzy control rule

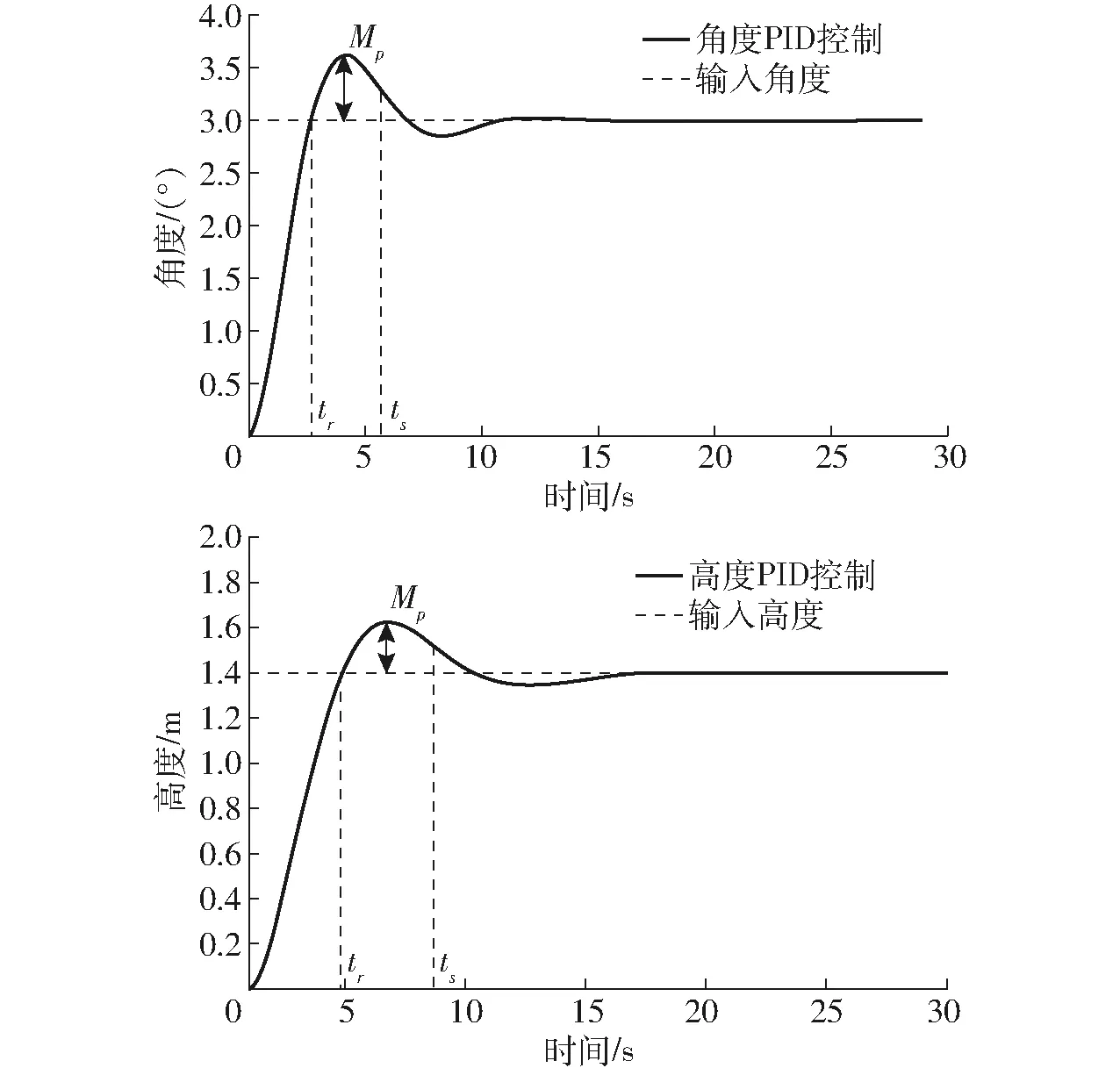
图6 单传感器PID控制仿真结果Fig.6 Simulation results of single sensor PID control

3.1.2两种控制算法台架试验对比

搭建20 m喷杆，进行5组角度PID控制算法和双传感器融合的模糊PID控制算法的台架对比试验，通过分析5个陀螺仪输出角度的响应曲线，验证PID整定参数的有效性；同时分析激光雷达输出高度的响应曲线，通过失稳时间(即喷杆进入稳态后再次离开稳态的时间)对比两种控制算法性能。

3.1.3喷杆水平度和稳定性判定

为研究车身振动和自然风速对喷杆水平度和稳定性的影响，采用5个星光极M1运动相机记录喷杆稳定后喷杆4、8、12、16、20 m位置处的高度，每隔1 s记录一次，统计稳定后10个不同时刻喷杆各点的高度情况。通过分析同一时刻各点高度值的标准差反映喷杆的水平度，分析10个不同时刻喷杆各点高度均值的变异系数反映喷杆的稳定性。

3.2 仿真试验

3.2.1PID控制参数整定

根据前文建立的无刷直流电机系统模型和所得到的传递函数，在Matlab的Simulink模块中建立PID控制系统的仿真模型[31]。将喷杆初始位置的角度和高度分别作为输入量，仿真过程中输出的角度和高度作为反馈量，通过PID控制算法闭环控制无刷直流电机的转速。在实际控制的过程中，比例系数决定系统的响应速度，Kp越大，响应速度越快，但超调量也会随之增大，过大的比例系数会导致系统不稳定；积分系数影响控制系统的精度，Ki越大，控制精度越高，但会增加系统的振荡次数；微分系数影响调节时间，同时影响超调量。分别对角度PID和高度PID进行多次仿真测试，其中几组测试结果如表2所示。

表2 PID控制参数整定Tab.2 PID control parameter settings

由表2可以看出，当角度PID和高度PID的控制参数Kp、Ki、Kd分别为0.2、0.000 3、0.2和0.12、0.000 1、0.18时，进入稳态的调节时间较短，超调量较小，控制性能相对较好。

图7 双传感器融合的模糊PID控制算法仿真模型Fig.7 Simulation model of fuzzy PID control algorithm based on dual sensor fusion

3.2.2双传感器融合的模糊PID控制算法仿真分析

由于喷杆较长，实际测试过程中不确定因素较多，单独采用陀螺仪进行基于角度PID的喷杆控制时，喷杆调节范围容易进入非调节区，造成喷杆失稳，将角度和高度两种传感器信息进行融合控制是解决角度PID控制进入非调节区的有效方法之一。

根据前文建立的模糊控制器，在Matlab的Simulink模块中建立双传感器融合的模糊PID控制算法仿真模型，如图7所示。将高度偏差E和角度偏差变化率EC作为模糊控制器的输入量，两组PID控制的权重比系数Q作为模糊控制器的输出量，根据在FUZZY Toolbox中提前设计好的FIS系统实时调整Q[32]，确定各个阶段所需的最优权重系数。

仿真过程中，权重比系数Q根据模糊控制规则表进行实时调整，模糊控制曲面图如图8所示。从图8可以看出，当角度偏差变化率EC较大时，Q较小，即角度PID控制占比大；当角度偏差变化率EC较小、高度偏差E较大时，Q较大，即高度PID控制占比大。由此验证了模糊控制算法在融合两种单一传感器PID控制中的有效性。

3.3 台架试验

3.3.1试验设计

喷杆自动调平控制系统台架试验于2021年10月30日在华南农业大学广东省农业航空应用工程技术研究中心进行。喷杆采用前述的自动调平控制系统进行控制，台架试验实物图如图9所示，关键部件局部图如图10所示。

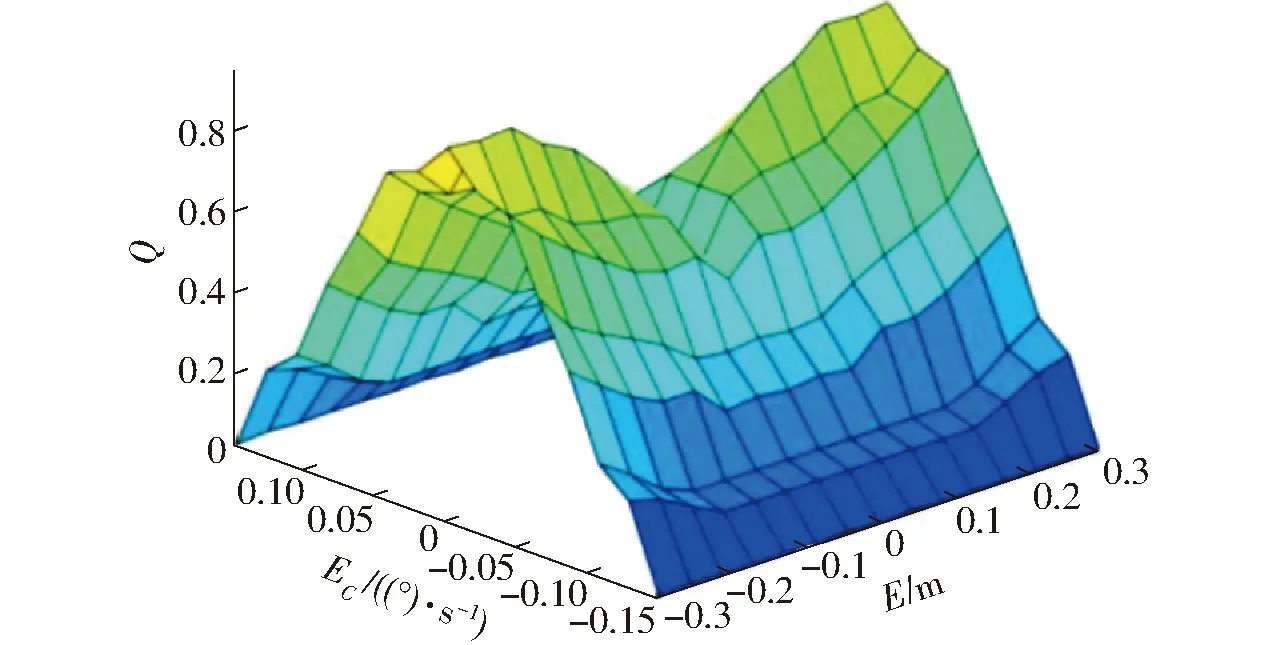
图8 模糊控制曲面图Fig.8 Fuzzy control surface diagram

图9 自动调平控制系统台架试验Fig.9 Bench test of automatic leveling control system1.喷雾机车身 2.安全台架 3.无刷直流电机 4.喷杆 5.喷杆连接件

图10 关键部件局部图Fig.10 Local view of key components1.喷头 2.激光雷达 3.陀螺仪 4.电调 5.无刷直流电机 6.桨叶

MPU6050型陀螺仪用于测量喷杆与水平面之间的角度，TFmini Plus型激光雷达用于测量喷杆距地面的高度，与控制电路组成闭环控制系统。由于喷杆较长，在自然状态下会出现挠曲变形，因此利用5组角度PID控制算法对喷杆进行控制。在喷杆3、7、11、15、19 m位置各安装一个陀螺仪测量喷杆在该位置的角度，在6 m和16 m的位置各安装一个激光雷达测量喷杆高度，将测量值作为相应位置的反馈量。

以喷杆初始位置的角度和高度作为初始量，喷杆水平位置的角度和高度作为目标量；陀螺仪和激光雷达测量值作为反馈量，利用模糊控制算法融合角度PID和高度PID的输出值，自动调节电子调速器输出PWM信号占空比；进而控制电机转速，实现喷杆系统自动调平。

试验过程中，分别对角度PID控制算法、双传感器融合的模糊PID控制算法进行对比试验。

3.3.2试验结果与分析

电机开始转动时，利用串口助手XCOM每隔0.5 s记录陀螺仪和激光雷达输出的数据，分别得到两种不同控制算法的试验结果，如图11所示。选取前30 s的输出数据，把5个陀螺仪响应曲线的上升时间、进入稳态的调节时间、超调量取平均值进行分析，控制性能试验数据对比如表3所示。

由于20 m喷杆在调试过程中相互产生干涉等不确定因素，表3中试验数据与仿真结果相比，两种控制算法的上升时间分别增加了0.8 s和0.62 s，进入稳态的调节时间分别增加了10.61 s和8.34 s，超调量分别增加了0.65°和1.66°，但总体趋势与仿真结果保持一致，验证了前述PID参数的有效性。

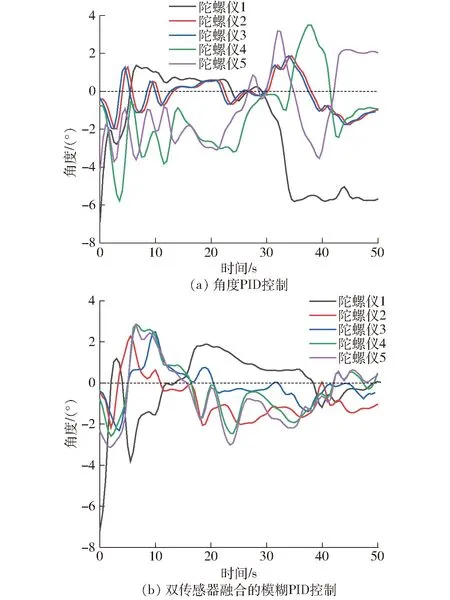
图11 两种控制算法试验输出的陀螺仪数据Fig.11 Gyroscope data output by two control algorithms

表3 控制性能试验数据对比Tab.3 Comparison of control performance test data

图12 两种控制算法的失稳时间对比Fig.12 Comparison of instability time between two control algorithms

由于喷杆较长、不确定性因素较多，为进一步对比两种算法的性能，利用激光雷达输出的高度进行了自动调平控制的失稳时间对比。

从图12中可以看出，采用5组角度PID单独进行喷杆调平控制时，易出现控制死区，使得喷杆进入失稳状态，本次试验测得的失稳时间为31.86 s。采用双传感器融合的模糊PID控制算法进行喷杆调平控制时，模糊控制算法将高度PID与角度PID输出量融合，当角度传感器PID控制算法进入控制死区无法进行喷杆调节时，激光雷达的高度PID控制算法发挥作用，使角度PID控制算法脱离控制死区，避免出现图12自动调平控制失稳的状况。

3.4 田间试验

3.4.1试验设计

为研究在自然风干扰和车身在高程上振动的影响下，喷杆自动调平控制算法的有效性，2022年1月5日，在华南农业大学增城教学科研基地进行了旋翼悬浮式喷杆喷雾机喷杆自动调平控制算法的田间试验。试验期间，天气多云，空气湿度69%，温度9～19℃，东北风2级以下，试验现场如图13所示(由于喷杆较细长，原图背景复杂造成喷杆及测量工具不清晰，图13a进行了背景优化处理)。

图13 田间试验Fig.13 Field experiment1.喷杆 2.运动相机 3.三脚架 4.标尺

试验采用课题组自制的旋翼悬浮式喷杆喷雾机样机，该样机以3WP-100型自走式喷杆喷雾机为应用平台，喷杆采用薄壁方形截面为30 mm×30 mm、壁厚为1.5 mm的方管。其他试验测量设备包括：星光极M1运动相机及三脚架(用于记录采样点喷杆动态的影像)、标尺(用于测量喷杆的动态真实高度)等。

为记录喷杆自动调平控制时的动态活动情况，在喷杆4、8、12、16、20 m位置的正前方5 m处分别设立一根标尺，同时在这几个位置上相应放置三脚架，将星光极M1运动相机安装在三脚架上。调整三脚架高度，使其与车身和喷杆铰接点高度保持一致，保证喷杆自动调平后运动相机镜头平视喷杆，以便记录喷杆各方管的真实高度。

3.4.2试验结果与分析

读取同一时刻各个运动相机影像中喷杆对应标尺的高度，每隔1 s获取一次，得到多个不同时刻喷杆实际高度折线图，如图14所示。

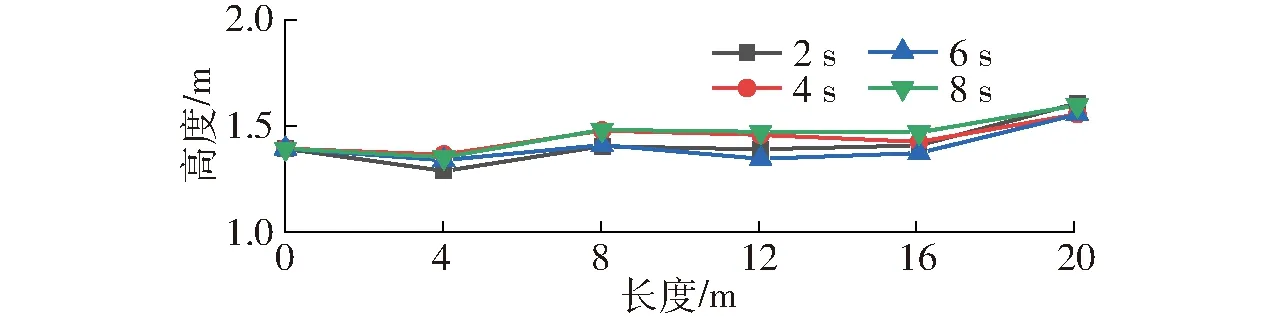
图14 不同时刻喷杆实际高度对比曲线Fig.14 Actual height line chart of spray boom at different times

由表4可知，当喷杆进入稳定状态后，整根喷杆各点高度均值在1.4～1.5 m之间浮动，标准差最大为0.102 7 m，具有较好的水平度；所采集的10个不同时刻喷杆各点高度均值的变异系数为1.40%，说明喷杆悬浮高度的稳定性较好。但由于传感器自身的固有缺陷及田间作物冠层稀疏且高差变化大等原因，在进行多次田间试验的过程中，偶尔会出现控制过于灵敏而造成喷杆悬浮调整过度的情况。

表4 20 m喷杆各时刻高度Tab.4 Height of 20 m spray boom at each moment

4 结论

(1)针对现有大型喷杆喷雾机喷杆桁架结构存在的不足，分别融合地面机械高续航、载重大和空中无人机作业灵活、不受地形地貌限制小的优点，提出了一种旋翼悬浮式喷杆。通过对喷杆结构的受力情况以及控制原理理论分析，设计了一套完整的喷杆自动调平控制系统，并搭建了整机试验平台；采用“陀螺仪+激光雷达”进行双传感器融合控制的方式，实现闭环控制旋翼喷杆上各旋翼的转速，达到喷杆自动调平控制，保持水平状态。

(2)在Matlab的Simulink模块中分别对角度PID和高度PID进行参数整定，同时对设计的模糊控制器进行了仿真试验。对仿真参数进行台架试验验证，试验结果表明：采用双传感器融合的模糊PID控制算法优于单传感器的角度PID控制算法，可避免出现失稳状态。

(3)对喷杆自动调平控制系统进行了田间试验验证。试验结果表明：当喷杆进入稳定状态后，整根喷杆各点离地高度均值在1.4～1.5 m之间，标准差不大于0.102 7 m，具有较好的水平度；所采集的10个不同时刻喷杆各点高度均值的变异系数为1.40%，说明喷杆悬浮高度的稳定性较好。本研究验证了旋翼悬浮式喷杆作业方法的可行性，可为旋翼悬浮式喷杆喷雾机的样机研制提供参考。