基于面元模型的非刚性动态场景重建方法研究

王欢　门涛　苏宏鲁　王忠生　姜勇

摘要：场景目标几何变形和运动的同时表述是非刚性动态场景重建的一个关键问题，出现遮挡、开—合拓扑变化、快速运动等情况都可能导致场景重建失败。针对这一问题，研究提出了一种基于面元模型的非刚性动态场景重建方法，利用基于权值算法的深度相机点到平面迭代最近点（Iterative Closest Point，ICP）算法改进了已有系统非刚性变形场估计中ICP能量函数的求解过程。与基于SDF模型的重建方法相比较，基于面元模型的方法支持在线高效更新，占用计算资源更少，更加轻量化。在VolumeDeform数据集上的对比实验表明，改进后的方法提高了系统的鲁棒性，重建的模型更加完整。

关键词：面元模型;非刚性动态场景;深度相机;场景重建

中图分类号：TP242    文献标志码：A    文章编号：1671-0797（2022）02-0071-05

DOI：10.19514/j.cnki.cn32-1628/tm.2022.02.020

0    引言

非刚性动态场景重建问题是当前三维场景重建领域的一个研究热点，从利用场景特定先验的方法到在较少约束下基于模板和无模板的重建方法，许多研究者一直活跃在这一领域。非刚性ICP算法[1]最初是针对二维非刚性配准问题提出的，后来扩展到三维非刚性配准中[2]。第一个可以跟踪复杂变形的非刚性配准方法[3-4]使用变形代理来解耦优化问题的维度和模型复杂性，但仍然需要离线运行。近年来，许多鲁棒离线的模板跟踪方法利用关键帧和鲁棒优化算法[5-6]，允许变形场的不连续，更适合关节运动的跟踪问题。

在不使用强先验的情况下，对任意一般变形对象的在线跟踪是最近才实现的。Zollhfer等人[7]提出的基于模板的非刚性跟踪方法，采用一种由粗到细分层次的GPU优化策略，使实时性成为可能。这种方法的输入是由一个定制的RGB-D传感器捕获的高质量颜色和深度流。在获取模板后，利用高性能图形处理器的数据并行计算能力和由粗到细分层次的GPU优化策略，通过鲁棒优化实现了非刚性物体运动的实时跟踪。虽然这种方法可以实时跟踪一般的目标，但必须预先获得模板模型。为每个场景获取这样的模板非常耗时，这就限制了该方法的实用性。

如果不能预先获得目标的模板模型，则需要解决更具挑战性的几何变形和运动重建问题。鲁棒地分离物体的形状和运动是一个模糊问题，因为两者都可以解释观察到的变化。许多离线方法将时间三维重建看作是一个四维时空优化问题[8-9]，通过小变形和小帧间运动的设定使问题得以简化处理[10]。第一个解决实时无模板重建问题的方法是Newcomebe等人提出的DynamicFusion方法[11]。这种方法能够基于消费级深度相机来联合重建场景目标的几何变形和运动。首先建立一个在关键帧下的模型，之后场景发生的变化都可以通过几何变换对应到这个模型上，新读取的深度图都通过几何变换再融合到模型当中，在配准中其误差项除刚性配准误差项外还有正则项，正则项可以很好地处理非刚性的配准。VolumeDeform[12]是DynamicFusion的扩展，利用细尺度变形图替代粗尺度变形图来参数化变形场，从而达到更高的重建质量。为了实现实时帧率，该方法采用了一种分级的从粗到细的数据并行GPU优化策略。此外，将稀疏特征匹配融合到场景目标中，实现了更强的鲁棒跟踪。

Dou等人[13]提出的Fusion4D方法可以实时获得变形场景的完整、瞬态重建模型。它基于一个复杂的多视角设置，由8个视角组成，每个视角由2个红外和1个彩色相机组成。这种方法的特别之处在于采用了关键体策略，使得该方法对故障跟踪具有鲁棒性。该方法不是将参考体固定在第一个输入帧上，而是定期将参考体重置到一个融合本地数据的关键體中。Fusion4D方法可以实现对任意非刚性场景的高速重建。其中一个关键因素是在输入和重建之间建立一个密集的三维对应场，使其能够稳健地处理快速运动的场景。

非刚性动态场景重建是具有很大难度的三维重建问题，不同于静态场景重建，场景目标的几何变形和运动的同时表述是其中一个关键。遮挡的出现、开—合拓扑的变化、快速运动等情况都可能使重建失败。目前的解决思路主要分为基于SDF模型和基于面元模型两种，研究者们提出了很多解决方法，如使用模板或先验信息、加入特征点和光照反射率约束、多视角等。

本文基于深度相机点到平面ICP算法改进了已有系统非刚性变形场估计中ICP能量函数的求解方法，提出了一种基于面元模型的非刚性动态场景重建方法，实验表明，该方法提高了系统的鲁棒性，重建的模型更加完整。

1    非刚性场景重建的总体架构

1.1    符号定义

深度相机获取的深度图像序列记为{Dt}，其中t是帧标签。顶点图V是一个图像，每个像素记录一个3D位置;同样地，法线图N是一幅每个像素都记录法线方向的图像。采用DynamicFusion[11]中的方法将变形场W表示为节点图，与体积变形场相比，该节点图稀疏但有效。更具体地：

W={[Pj∈R3，σj∈R+，Tj∈SE（3）]}        （1）

式中：j为节点的索引;Pj为第j个节点的位置;σj为半径参数;Tj为第j个节点的变换矩阵。

为了更好地插值，Tj用双四元数j表示，对于一个3D点x，在x处W的变形可以插值为：

W（x）=normalizedwk（x）k        （2）

其中，N（x）为点x的最近邻集，权值：

wk（x）=exp[-||x-pk||22/（2σk2）]                （3）

面元s是由位置v∈R3，法向量n∈R3，半径r∈R+，置信度c∈R，初始化时间tinit∈N和最近观察的时间tobserved∈N组成的元组。用大写字母S表示面元数组，S[i]是这个数组中的第i个面元。在变形场W的作用下，面元可以通过式（4）、式（5）进行变形。

vlive=W（vref）vref                       （4）

nlive=rotation[W（vref）]nref            （5）

其中，vlive和nlive是变形后点的位置和法向量，vref和nref是变形前点的位置和法向量，其他属性，如半径、时间、置信度等，变形后保持不变。

1.2    场景重建的流程架构

如图1所示，系统以逐帧的方式处理输入的深度流。在接收到新的深度图像后，首先计算变形场，使参考帧与当前的深度观测对齐。初始化前一帧的变形场，然后采用类似于Newcombe等人[14]提出的ICP算法进行优化。一旦变形场被更新，就执行数据融合，将当前的深度观测数据累积到一个全局几何模型中。

与之前方法最大的不同之处在于，在整个方法中采用了一种有效的基于面元的几何和变形场表示。系统维护两个面元组，一个在参考帧sref中，另一个在实时帧slive中。变形场W在参考帧中定义，给定适当维护的最近邻集和权值，可以定义变形场的逆为：

vref =W（vref）-1vlive                  （6）

nref =rotation[W（vref）]-1nlive            （7）

其中，变形W（vref）可以通过查询N（sref）和{W（sref）}计算得到。

因此，与在参考帧中进行几何更新不同，本文的方法在实时帧中更新几何模型并将它们变形回参考帧中。

2    三维场景重建算法

2.1    深度图预处理

首先对获取的深度图进行双边滤波（bilateral filter）处理，双边滤波是一种可以达到保持边缘、降噪平滑效果的滤波器。和其他滤波原理一样，双边滤波也是采用基于高斯分布加权平均的方法，之所以可以达到保边去噪的效果，是因为滤波器由两个核函数构成：一个函数是由几何空间距离决定滤波器系数，考虑像素的欧式距离，即空间域（spatial domain S）;另一个函数是由像素差值决定滤波器系数，考虑像素范围阈的辐射差异，即范围域（range domain R）。

双边滤波的核函数是空间域与像素范围域的综合结果：在图像的平坦区域，像素值变化很小，对应的像素范围域权重接近于1，此时空间域权重起主要作用，相当于进行高斯模糊;在图像的边缘区域，像素值变化很大，像素范围域权重变大，从而保持了边缘的信息。

BF[I]p=G（||p-q||）G（|Ip-Iq|）Iq       （8）

其中，σs定义了滤波一个像素空间域的大小，σr控制了范围阈中由于强度差而使相邻像素向下加权的程度。

使用u=（x，y）T∈R2表示像素坐标。在每个像素u处，计算面元sdepth，首先通過V（u）=D（u）K-1（uT，1）T将深度值D（u）转换成面元sdepth处的位置V（u），K是深度相机的内参矩阵。然后这个像素点的法向量N（n）通过顶点图V使用中心差分估计得出。面元sdepth的置信度为c=exp[-γ2/（2？准2）]，其中γ是当前深度测量归一化后的径向距离。和Whelan等人[15]的方法类似，面元sdepth的半径r为：

r=                （9）

式中：d=D（u）为深度值;f为相机焦距;nz为法向量的Z轴分量。

2.2    深度图融合和变形场更新

假设已经得到了一个变形场，深度图融合和变形场更新流程首次在当前帧中执行数据融合，然后将当前面元变形回参考帧中，之后根据新观察的参考面元更新变形场。

2.2.1    当前帧中的融合

在求解变形场后，首先在参考面元组sref上执行一个前向变形，以获得与深度观测对齐的当前面元组slive。然后，使用类似Keller等人[16]的方法将深度图与当前面元融合。比较特别的是，当前面元组slive将渲染到索引图I中：给定相机内参K，每个当前面元slive[k]被投影到当前相机视角下的图像平面中，其中存储了各自投影点的索引k。在索引图I中，面元被渲染为未确定大小的点，也就是说，每个面元最多只能被投影到一个像素。索引图是超采样的深度图，以避免附近的面元投影到相同的像素。在实现过程中使用了一个4×4的超采样索引图。

对于深度图D中的每个像素，在索引图I上通过以u为中心的4×4窗口搜索，最多识别出一个与u处深度观测相对应的实时面元slive。查找相对应面元的准则如下：

（1）丢弃到深度顶点的距离大于δdistance的面元;

（2）丢弃法向量不与深度图法向量对齐的面元，dot（ndepth，nsurfel）<δnormal;

（3）对于剩下的面元，选择置信度高的;

（4）如果有多个这样的面元，选择最接近sdepth的那个。

如果找到了对应的面元slive，u处的深度面元sdepth将通过如下公式融合到slive中：

clive_new=clive_old+cdepth           （10）

vlive_new=（clive_old vlive_old+cdepth vdepth）/clive_new      （11）

nlive_new=（clive_old nlive_old+cdepth ndepth）/clive_new       （12）

tobserved=tnow                       （13）

rlive_new=（clive_old rlive_old+cdepth rdepth）/clive_new      （14）

式中：c、v、n、t和r分别为面元的置信度、顶点、法向量、最近观察到的时间点和半径。

2.2.2    实时面元再获取

对于深度图像素u，如果没有找到相对应的实时面元slive，该深度图面元sdepth将被附加到slive面元组中以完成几何重建。这需要计算最近邻集N（sdepth）和权重，将sdepth这个面元变形回参考帧中。但节点图G定义在参考帧中，在知道sdepth变形回去的位置之前计算在参考帧中的最近邻集N（sdepth）并不可行。

解决这个矛盾的一个方法是首先将节点图G变形回实时帧中，然后在实时帧中再执行面元获取。但是，在开—合拓扑变化时，面元sdepth可能被附加到不一致的节点。为了解决这一问题，提出以下准则：

（1）在实时帧中使用节点图给面元sdepth计算一个初始化最近邻集N（sdepth），node0_live∈N（sdepth）表示离面元sdepth最近的节点;

（2）对于任何node1_live∈N（sdepth），i≠0，如果：

1-ε<<1+ε           （15）

式中：阈值ε表示内在变形的程度。

则将nodei_live留在N（sdepth）中，否则移除该节点。

2.2.3    開—合拓扑变化问题

在开—合拓扑变化下直接进行数据融合会产生错误曲面，可以通过压缩变形场或者在体素方法中碰撞体素解决。本文的解决方法是在实时帧上限制反变形场的灵敏度，并去除实时帧中>1+ε的面元。

正如Dou等人[13]所提到的，不可能从一个参考帧来解释所有的运动，并且非刚性跟踪永远不会失效是不可能的。因此，Fusion4D方法使用了两个TSDF体，一个用于参考帧，另一个用于实时帧，并通过实时帧来恢复参考帧以处理幅度大的运动，跟踪故障和开—合拓扑变化。然而，维护额外的TSDF体和关联的最近邻场将增加计算成本和内存的使用。

本文以一种更紧凑、更有效的方式实现类似的想法：从深度观测推断出错误的面元比推断出错误的TSDF值更明确且更容易。该方式丢弃了任何从当前相机视角中可以看到但没有相应深度观察的实时面元slive，通过将实时面元slive投影到深度图中并进行窗口搜索来识别其对应关系。清理slive后，将sref重置为slive，并初始化其变形场。

2.3    非刚性变形场估计

给出新的深度图观测D、之前的变形场Wprev、几何模型sref和slive（通过Wprev将sref变形为slive），可以进行SE（3）变形Tj∈W的估计。为了执行该估计，首先预测实时面元slive的可见性，然后根据DynamicFusion方法将变形估计转化成优化问题。

可见性预测和Keller等人[16]的方法类似：将实时面元slive渲染为重叠的、圆盘状的有实时面元slive位置vlive、法向量nlive和半径rlive的表面元板。

与刚性SLAM不同的是，为了有效地查找最近邻点和权重，使用与深度图相同的分辨率渲染索引图I。而且，为了改进变形场估计在slive对离群点的鲁棒性，只渲染稳定的面元。在模型重新初始化后的前几帧，还渲染了最近观察到的面元。

遵循DynamicFusion方法，本文解决了如下优化问题来估计SE（3）的变换Tj∈W：

Etotal（W）=Edepth+λEregulation    （16）

式中：Edepth为约束变形与输入的深度D一致的数据项;Eregulation为使非刚性运动规则化的正则项，使其尽可能地刚性;λ为一个常数值，以平衡两个能量项。

Edepth是一个点到面的能量函数，这里可以写成：

Edepth（W）=[ndepthT（vmodel-vdepth）]2  （17）

式中：P为与模型和深度图面元对应的集合;n和v为与面元关联的法向量和顶点。

在给定深度观测值D和渲染实时几何图形下，Eregulation是一个使非刚性运动尽可能刚性的正则项：

Eregulation（W）= ||Tj pj-Ti pj||22         （18）

式中：Nj為节点图中与第j个节点相邻的节点集。

优化问题（16）是一个非线性最小二乘问题，可以用GPU实现的Gauss-Newton算法求解。本文采用基于权值算法的深度相机点到平面ICP算法计算式（17）点到面的能量函数Edepth，改进后的系统在ICP算法求解时将对不稳定方向点施加更大的权重，增加配准时对几何特征单一区域的约束，且权值算法中深度二次衰减算法可以更好地处理重建系统中所使用的深度相机数据。

3    实验分析

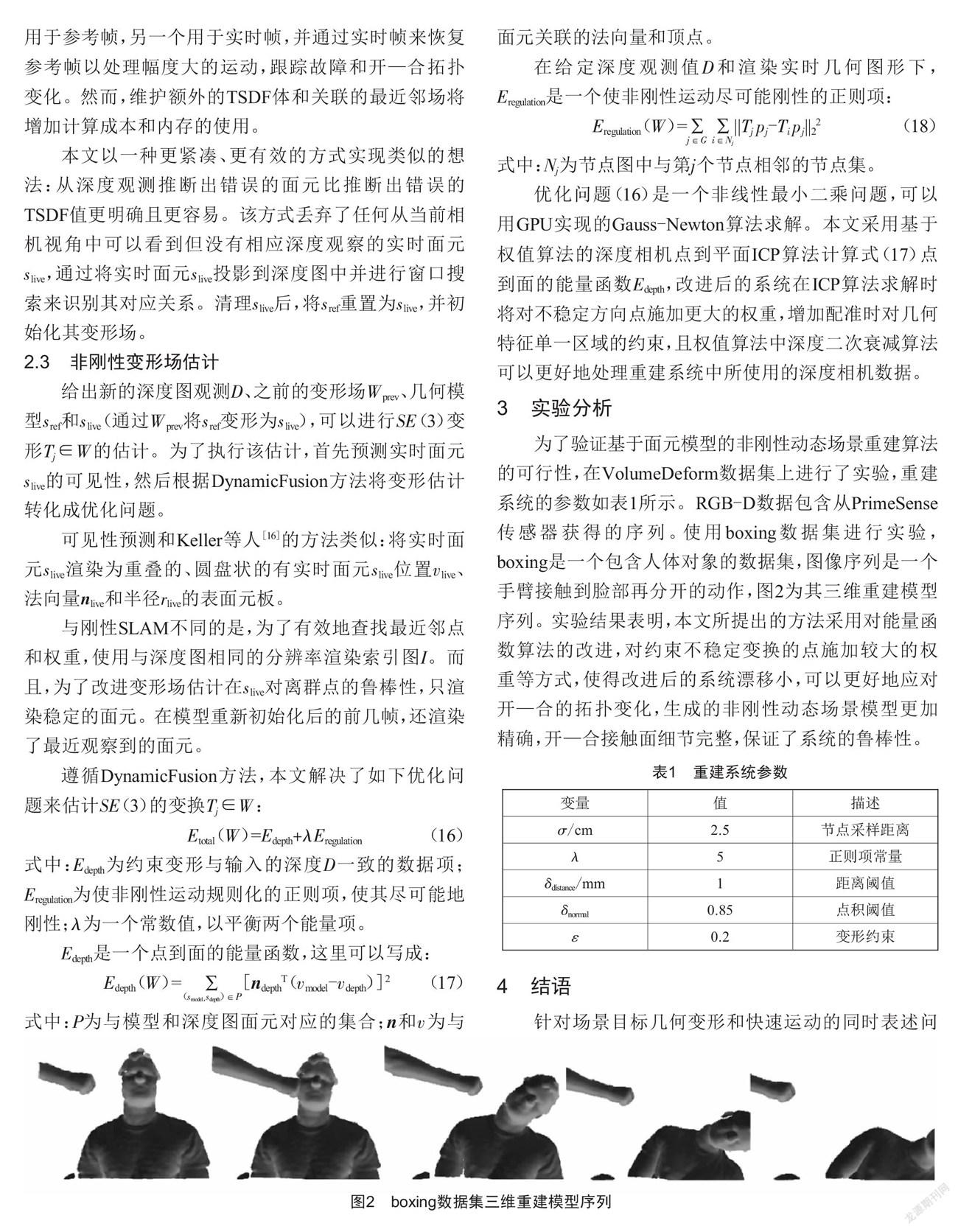
为了验证基于面元模型的非刚性动态场景重建算法的可行性，在VolumeDeform数据集上进行了实验，重建系统的参数如表1所示。RGB-D数据包含从PrimeSense传感器获得的序列。使用boxing数据集进行实验，boxing是一个包含人体对象的数据集，图像序列是一个手臂接触到脸部再分开的动作，图2为其三维重建模型序列。实验结果表明，本文所提出的方法采用对能量函数算法的改进，对约束不稳定变换的点施加较大的权重等方式，使得改进后的系统漂移小，可以更好地应对开—合的拓扑变化，生成的非刚性动态场景模型更加精确，开—合接触面细节完整，保证了系统的鲁棒性。

4    结语

针对场景目标几何变形和快速运动的同时表述问题，特别是出现遮挡、开—合拓扑变化等情况，研究提出了一种基于面元模型的非刚性动态场景重建方法，利用基于权值算法的深度相机点到平面ICP算法，对非刚性变形场估计中ICP能量函数的求解方法进行了改进。与基于SDF模型的重建方法相比较，基于面元模型的方法支持在线高效更新，占用计算资源更少，更加轻量化。在VolumeDeform数据集上的实验表明，改进后的方法解决了因开—合拓扑变换、遮挡等引起的场景重建信息缺失问题，提高了系统的鲁棒性，重建的模型更加完整。

[参考文献]

[1] PARAGIOS N，ROUSSON M，RAMESH V.Non-rigid regis-

tration using distance functions[J].Computer Vision and Image Understanding，2003，89（2/3）：142-165.

[2] FUJIWARA K，NISHINO K，TAKAMATSU J，et al.Locally rigid globally non-rigid surface registration[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision，2011：1527-1534.

[3] CHANG W，ZWICKER M.Range scan registration using reduced deformable models[J].Computer Graphics Forum，2009，28（2）：447-456.

[4] LIAO M，ZHANG Q，WANG H M，et al.Modeling deformable objects from a single depth camera[C]//2009 IEEE 12th International Conference on Computer Vision，2009：167-174.

[5] LI H，ADAMS B，GUIBAS L J，et al.Robust single-

view geometry and motion reconstruction[J].ACM Transactions on Graphics，2009，28（5）：1-10.

[6] GUO K W，XU F，WANG Y G，et al.Robust non-rigid motion tracking and surface reconstruction using

L0 regularization[C]//2015 IEEE International Conference on Computer Vision，2015：3083-3091.

[7] ZOLLH？魻FER M，NIE？覻NER M，IZADI S，et al.Real-time non-rigid reconstruction using an RGB-D camera[J].ACM Transactions on Graphics，2014，33（4）：1-12.

[8] MITRA N J，FL？魻RY S，OVSJANIKOV M，et al.Dynamic geometry registratio[C]//Proceedings of the Fifth Eurographics Symposium on Geometry Pro-

cessing，2007：173-182.

[9] S？譈？覻MUTH J，WINTER M，GREINER G.Reconstructing animated meshes from time-varying point clouds[J].Computer Graphics Forum，2008，27（5）：1469-1476.

[10] WAND M，ADAMS B，OVSJANIKOV M，et al.Efficient reconstruction of nonrigid shape and motion from real-time 3D scanner data[J].ACM Transa-

ctions on Graphics，2009，28（2）：1-15.

[11] NEWCOMBE R A，FOX D，SEITZ S.M.DynamicFusion： Reconstruction and Tracking of Non-Rigid Scenes in Real-Tim[C]// 2015 IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2015：343-352.

[12] INNMANN M，ZOLLH？魻FER M，NIE？覻NER M，et al.Volume-

Deform：Real-time volumetric non-rigid recons-

truction[C]//European Conference on Computer Vision，2016：362-379.

[13] DOU M S，KHAMIS S，DEGTYAREV Y，et al.Fusion4D： Real-time performance capture of challenging scenes[J].ACM Transactions on Graphics，2016，35（4）：1-13.

[14] NEWCOMBE R A，IZADI S，HILLIGES O，et al.Kinec-

tFusion：Real-time dense surface mapping and tracking[C]//2011 10th IEEE International Symposium on Mixed and Augmented Reality， 2011：127-136.

[15] WHELAN T，LEUTENEGGER S，SALAS-MORENO R，et al.ElasticFusion：Dense slam without a pose graph[C]//Robotics：Science and Systems （RSS），2015：1-9.

[16] KELLER M，LEFLOCH D，LAMBERS M，et al.Real-time 3D reconstruction in dynamic scenes using point-based fusion[C]// 2013 International Conference on 3D Vision，2013：1-8.

收稿日期：2021-10-27

作者簡介：王欢（1971—），男，辽宁鞍山人，教授级高级工程师，研究方向：冶金矿山信息化与自动化。