考虑部件不确定性的发动机性能裕度设计方法
计自飞,韩文俊,李瑞军,阎巍
(中国航发沈阳发动机研究所,沈阳 110015)
0 引言
在航空发动机的加工、装配、使用过程中均会产生部件和系统性能的不确定性,各部件性能不确定性累积叠加会导致发动机总体性能的非确定性。尤其是在极端和恶劣工作条件下,很小的部件性能偏差都将对整机性能产生极大影响[1]。在发动机研制初期就应充分考虑不确定性问题。为了保证性能达标,以往的做法是在发动机总体指标上直接留出一定裕度,该裕度的取值往往依赖于工程经验。对于新研发动机,由于新技术的应用,尚无足够的经验,裕度选取过大,将会导致过大的冗余设计,进而造成其他性能损失;裕度选取过小,则发动机总体性能仍存在较高的不达标风险。
部件参数不确定性对发动机总体性能的影响的量化分析,可以通过蒙特卡罗模拟(Monte Carlo Simulation,MCS)方法实现。Kurzke[2]利用蒙特卡罗方法模拟了燃气涡轮发动机的性能表征;Mavris等[3-5]利用概率方法研究了部件性能对发动机循环参数选取的影响,为发动机循环参数稳健性设计提供了参考;Kestner等[6-7]建立了响应面模型、贝叶斯网模型、神经网络模型等来发展稳健设计方法;陈敏等[8]利用蒙特卡罗模拟开展了部件性能不确定性在涡轴发动机性能分析中的量化研究;唐海龙等[9]基于涡轴发动机部件不确定性的量化分析模型,研究了控制规律变化和性能蜕化对涡轴发动机性能达标概率的影响;赵运生[10]以大涵道比涡扇发动机为研究对象,基于蒙特卡罗模拟研究了部件性能不确定性对整机性能达标概率的影响。以上研究主要基于发动机非线性模型开展,加上蒙特卡罗模拟需要足够大的样本数量才能获得有意义的结果[11],但过大的计算量和计算时间在工程上难以接受。
本文以混合排气涡扇发动机为研究对象,建立了航空燃气涡轮发动机性能参数裕度需求的确定方法。
1 数学物理模型
1.1 基本思路
部件和系统的不确定性可以通过部件参数表征,例如,效率、面积等。概率密度函数用于模拟各部件和系统性能的不确定性,使其能够在确定性的总体性能分析模型中传播。部件参数不确定性对发动机总体性能参数的影响分析原理如图1所示。

图1 部件参数不确定性对整机性能的影响分析原理
从图中可见,性能参数的不确定性客观存在。总体性能稳健设计的目的就是提高性能参数达标的置信度。考虑部件不确定性的发动机性能裕度设计实现途径如图2所示。从图中可见,单纯减小性能参数的不确定性,不能提高参数置信度;而通过在性能参数上留出合理的裕度,可以实现性能参数置信度的提高。可见,根据置信度需求确定合理的参数裕度需求是稳健设计的关键环节。
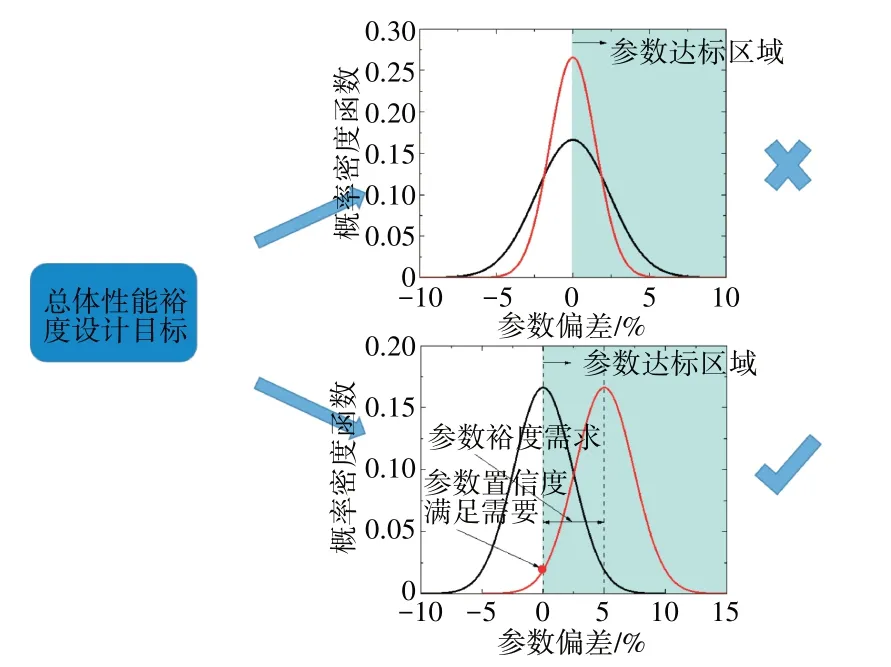
图2 考虑部件不确定性的发动机性能裕度设计实现途径
1.2 计算模型
根据分析,开展考虑部件不确定性的发动机性能裕度设计的基本步骤包括:不确定性定义→不确定性传播→不确定性量化→总体参数裕度确定,如图3所示。

图3 考虑部件不确定性的发动机性能裕度设计方法
(1)不确定性定义。
不确定性定义就是确定各部件参数的概率密度函数。概率密度函数用于模拟各部件和系统性能的不确定性,使其能够在确定性的总体性能分析模型中传播。假定标准正态分布N(0,1)的概率密度函数可表示为

假定各部件和系统参数不确定性分布符合正态分布,则其性能参数偏差量的样本N为
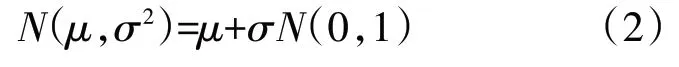
式中:μ为样本的均值;σ为样本的标准差。
(2)不确定性传播。
部件和系统参数不确定性的传播通过发动机的数学物理模型实现。本文以小涵道比混合排气涡扇发动机为研究对象。根据部件共同工作原理[12-13],发动机在非设计点工作时必须满足6个平衡方程,即低压轴功率、高压轴功率、混合室内外涵静压、燃烧室与高压涡轮流量、高压涡轮与低压涡轮流量、低压涡轮与尾喷管流量平衡方程。以上6个平衡方程构成发动机稳态模型的数学基础,写成参数形式为

式(3)可通过Newton-Raphson方法迭代求解。写成微分形式为

用差商代替微商,则式(4)变为

式中:M为6阶系数矩阵。
由式(5)得到ΔX后,k+1次迭代的变量值修正为

如此反复,不断修正独立变量的值,直至平衡方程误差满足设定精度要求。
下面通过与GasTurb 13软件计算结果的比较,验证根据上述方法建立的发动机模型的精度和可靠性。对于总压比为32、涵道比为0.4、涡轮前温度为1800 K的混合排气涡扇发动机,在地面起飞状态下,保持推力恒定,开环调整中间状态喷管喉部面积,则不同面积对应的涵道比计算结果见表1。通过对比可见,本文模型计算结果与GasTurb计算结果的误差均在1%以内,说明本文所建模型合理、可行,且具有较高精度,可完成部件和系统参数不确定性的传播和量化。
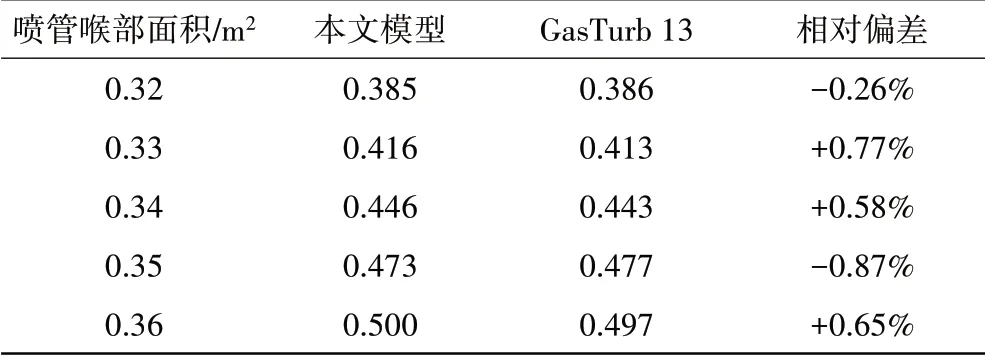
表1 发动机非线性模型验证
(3)不确定性量化。
蒙特卡罗模拟是研究不确定性量化的经典方法。采用蒙特卡罗方法量化模型不确定性时,样本数量要足够大,才能得到可靠的结果[11]。因此,采用传统的航空燃气涡轮发动机的总体性能分析模型作为目标函数会导致计算量极大。由文献[14]可知,生产、装配等因素导致的部件效率等参数的偏差量均在±1%以内。部件和系统偏差在±1%以内时,基于建立的发动机非线性性能仿真模型获得的发动机地面起飞状态性能参数对部件参数的敏感性分析结果如图4所示。从图中可见,在小偏差范围内,整机性能随各部件和系统参数偏差量的变化基本呈线性变化,曲线的斜率越大,说明性能参数对该部件参数偏差量越敏感。这一点可以通过将发动机性能参数关于部件和系统参数的表达式进行Taylor展开,并略去高阶项的方法验证。因此,可以利用总体性能参数对部件参数的敏感性系数矩阵(见表2)替代航空发动机非线性模型,开展部件参数不确定性的量化分析,从而在保证精度的同时,大大减小计算量。该方法称为敏感性系数矩阵方法(Sensitivity Coefficient Matrix Method,SMM)。


图4 发动机总体参数对部件参数的敏感性
各部件和系统参数的综合影响用和方根(Root Sum Square,RSS)方法求解(表2)。表中部件参数偏差量一栏换成不同置信度下各部件参数相比于均值的最大变化量的绝对值,即可得到不同置信度对应的发动机总体性能参数的最大偏差量。根据和方根方法的理论可知,各部件参数偏差量的置信度直接影响发动机总体参数偏差量的置信度。为了评估表2中敏感性系数矩阵的可靠性,利用成熟软件GasTurb 13计算了相同输入条件下的计算结果,见表3。表2、3对应单项与和方根结果的偏差均在0.03%以内,从而证实了表1中的敏感性系数矩阵的可靠性。

表2 总体性能参数对部件参数的敏感性系数矩阵(本文方法)

表3 总体性能参数对部件参数的敏感性系数矩阵(GasTurb 13)
1.3 模型验证
为了验证上述方法的合理性,对采用蒙特卡罗法获得的发动机推力和耗油率概率分布与采用敏感性系数矩阵方法获得的结果进行对比,2种方法获得的发动机总体参数概率分布如图5所示,其中蒙特卡罗法的样本容量选取为20000。从图中可见,2种方法获得的发动机总体性能参数概率分布吻合良好,从而证明了敏感性系数矩阵方法的合理性,可用于不确定性的量化和总体性能参数裕度需求的确定。
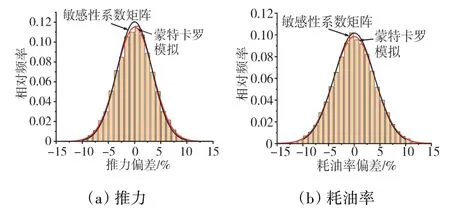
图5 2种方法获得的发动机总体参数概率分布
2 结果与讨论
与试验测试不同,无论如何精确和复杂的性能分析模型都无法自动考虑不确定性的影响。为此,将不确定分析融入发动机性能分析模型,可为发动机性能不确定性分析以及性能裕度设计提供依据[15]。按照确定性模型开展方案设计,只能保证发动机平均性能达标,即发动机性能达标的置信度只有50%,这显然不满足项目要求。为此,在设计中必须留出一定的性能裕度,使得发动机性能参数的置信度达到更高值。以给出的小涵道比涡扇发动机为研究对象,选取地面起飞状态为设计点,部件和系统参数的偏差量按照文献[14]中的方法考虑,进一步研究发动机总体性能参数裕度需求的确定及其影响因素。
2.1 总体性能达标置信度对裕度需求的影响
根据部件和系统参数的不确定性分布,采用敏感性系数矩阵方法得到发动机总体性能参数的不确定性分布,为简化分析,本文使用参数的相对偏差量代替参数的绝对量进行分析,如图6、7所示。对于推力而言,达标的标准是样本值大于目标值;而对于耗油率而言,达标的标准是样本值小于目标值。因此二者的累积概率曲线的形状不同。
从图中可见,性能参数达到某一置信度对应的数值相比于均值(即性能指标)的偏差即可作为该性能参数的设计裕度。采用SMM和MCS方法计算得到的不同置信度对应的地面起飞状态总体参数裕度需求见表4、5。从表中可见,采用2种方法得到的计算结果吻合良好,进一步证实了本文建立的敏感性系数矩阵方法的有效性。总体性能参数满足设计要求的置信度越高,其需要留出的裕度越大。这一点可以由图6(b)和图7(b)直观解释,图中不同颜色的曲线分别代表不同置信度下的推力不确定性分布。与基准发动机(参数裕度为0,性能达标置信度50%)的偏差越大,意味着裕度需求越大,则样本在性能达标区的占比越大,即性能达标的置信度越高。

表4 不同性能置信度对应总体参数裕度需求(SMM)
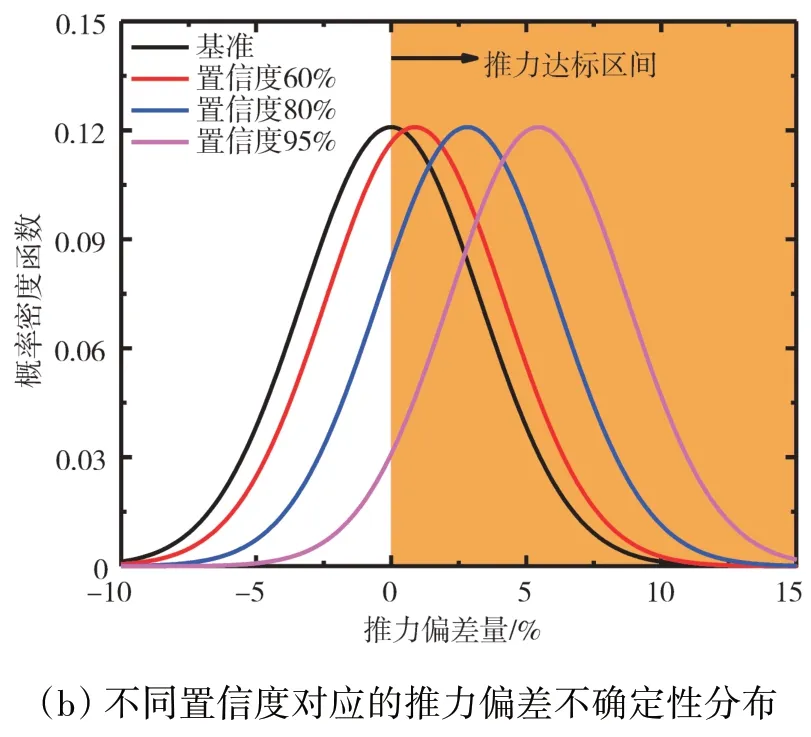
图6 性能达标置信度对推力裕度需求的影响

图7 性能达标置信度对耗油率裕度需求的影响


表5 不同性能置信度对应总体参数的裕度需求(MCS)
在地面起飞状态下,当发动机性能指标的置信度设置为60%时,推力和耗油率裕度需求分别为0.88%和-1.00%;当发动机性能指标的置信度设置为80%时,推力和耗油率裕度需求分别为2.82%和-3.33%;当发动机性能指标的置信度设置为95%时,推力和耗油率裕度需求分别为5.45%和-6.65%。需要注意的是,以上定量结论是基于本文设定的发动机循环参数计算得出的,该方法可推广应用于不同发动机,具体量化结果需要根据相应发动机的循环参数进行评估。
2.2 部件参数达标置信度对裕度需求的影响
压气机效率不确定性分布的标准差与置信度的关系如图8所示。在某一特定区间内,部件参数不确定分布的标准差越小,则参数落入该区间的置信度越高。因此,可用部件参数不确定性分布的标准差来表征部件参数的置信度。以前文所用各部件参数不确定性分布的标准差为基准,在此基础上乘以不同系数,构成3种不同的部件参数置信度。考虑将发动机总体性能参数的置信度目标设定为80%,则按照前文确定性能参数裕度的方法,利用2种方法计算的不同部件参数置信度对应的发动机地面起飞状态性能参数裕度设计结果见表6、7。

图8 压气机效率不确定性分布的标准差与置信度的关系
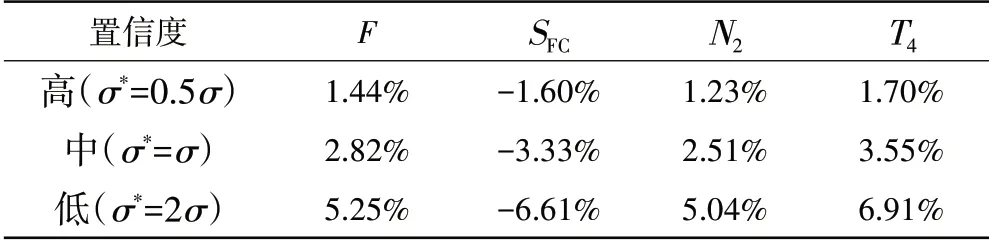
表6 不同部件参数置信度对应总体参数裕度需求(SMM)
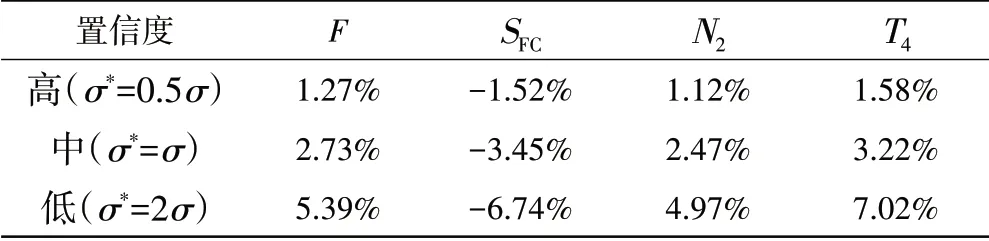
表7 不同部件参数置信度对应总体参数裕度需求(MCS)
从表中可见,2种方法的计算结果吻合良好,进一步证实了本文建立的敏感性系数矩阵方法的有效性。部件参数置信度对推力和耗油率裕度需求的影响如图9、10所示。根据定量结果,部件参数满足设计目标的置信度越高,总体性能参数需要留出的裕度越小。这一点的物理含义可以通过图9(b)和图10(b)进行解释。当总体性能参数达标的置信度相同时,总体性能参数的概率密度曲线越“瘦高”,则该分布的均值与性能指标的差值越小,意味着性能参数的裕度需求越小。就正态分布而言,概率密度曲线越“瘦高”,则要求各部件和系统参数的标准差越小,意味着部件和系统参数达标的置信度越高(图8)。

图9 部件参数置信度对推力裕度需求的影响

图10 部件参数置信度对耗油率裕度需求的影响
在地面起飞状态下,将各部件参数的标准差增大1倍,则推力裕度需求增加86%,耗油率裕度需求增加98%;将各部件参数的标准差减小50%,则推力裕度需求减小49%,耗油率裕度需求减小52%。该定量结论是基于本文设定的发动机循环参数计算得出的,该方法可推广应用于不同的发动机,具体量化结果需要根据相应发动机的循环参数进行评估。
上述部件参数不确定性对发动机性能参数影响分析的结果,为发动机总体性能参数裕度设计提供了理论依据。性能参数裕度需求的确定,需要考虑各方面的因素来综合确定。在方案设计初期,总体性能参数裕度的设计需要考虑发展潜力、性能衰退、安装损失、部件参数不确定性等多方面[16-18],本文主要关注考虑部件参数不确定性的发动机性能参数裕度设计。对于输出功率的地面燃机,可以通过放大尺寸来留出足够的功率裕度;而提供推力的航空发动机,其推力裕度需求会受到质量和迎风面积的严格限制,考虑到竞争性采购等因素,耗油率指标的裕度也不宜过大。
3 结论
(1)在加工、装配等环节导致的部件和系统参数偏差范围内,航空发动机总体性能偏差量随各部件和系统参数偏差量的变化基本呈线性变化,曲线的斜率越大,说明性能参数对该部件偏差量越敏感。耗油率对于部件效率和引气比例的偏差更加敏感,而推力对于尾喷管喉部面积的偏差更加敏感。
(2)对于各部件参数的不确定性满足正态分布,且各参数之间不相关的情形,部件参数不确定性对发动机总体性能参数的影响量化分析可通过敏感性系数矩阵方法实现。由于部件参数不确定性导致的总体性能参数偏差分布同样满足正态分布,并且部件参数的置信度决定了发动机总体性能参数的置信度。
(3)部件参数不确定分析结果为总体性能参数裕度设计提供了依据。部件参数满足设计目标的置信度越高,总体性能参数需要留出的裕度越小。部件参数置信度可由不确定性分布的标准差来表征,对于本文的算例发动机,在地面起飞条件下,若部件参数分布的标准差增大1倍,则推力裕度需求增加86%,耗油率裕度需求增加98%;若部件参数分布的标准差减小50%,则推力裕度需求减小49%,耗油率裕度需求减小52%。
(4)总体性能参数满足设计要求的置信度越高,其需要留出的裕度越大。在地面起飞条件下,推力指标置信度分别达到60%、80%和95%对应的裕度需求分别是0.88%、2.82%和5.45%;耗油率指标置信度分别达到60%、80%和95%对应的裕度需求分别是-1.00%,-3.33%和-6.65%。
利用本文所建立的方法,可以在计算量较小的前提下获得考虑部件参数不确定性的发动机总体性能裕度选取值。但本方法仅适用于部件和系统参数的不确定满足正态分布,且各部件参数不相关的情况。若存在某一部件参数的不确定性为非对称分布,则本方法不再适用,需要借助蒙特卡罗模拟来开展相关研究。同时,本文重点讨论原理和方法,定量结果主要基于算例发动机工作参数得出,若要推广用于其它发动机,则需更新算例发动机工作参数。

