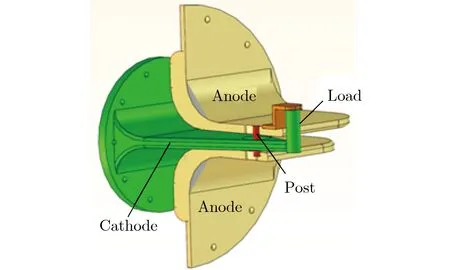
高功率单孔柱-孔汇聚传输结构阴阳极间隙闭合速度理论分析
吴撼宇,魏 浩,张鹏飞,邱孟通,王亮平,杨海亮,来定国,徐启福,楼 成,杨 森
(强脉冲辐射环境模拟与效应国家重点实验室; 西北核技术研究所: 西安 710024)
高电压、大电流高功率脉冲常应用于高能密度物理[1]、惯性约束聚变[2-5]、辐射效应物理[6]和冲击波物理[7-9]等领域的科学研究。脉冲功率装置多采用多路Marx或LTD(linear transmission driver)并联的拓扑结构以产生数十兆安的大电流脉冲。磁绝缘传输线(magnetically insulated transmission lines, MITLs)是大型脉冲功率驱动源的重要部件,可传输和汇聚高功率脉冲。位于MITLs末端的柱-孔汇聚结构(post-hole convolute, PHC)可将多路高功率脉冲合并为一路,再经一段圆盘传输线被馈送至负载[10-17]。
在Saturn(~8 MA)上的实验表明,MITLs和PHC能有效传输和汇聚高功率脉冲[15-16]。但是Z装置(~26 MA)上的实验结果表明,在PHC上存在大量的电流损失[18-21]。实验表明,当堆栈电流达到22 MA时,PHC附近损失电流的峰值达到4 MA,损失比例达18%。PHC的电流损失问题极大地约束了下一代大型脉冲功率源技术的发展。为提高PHC的电流传输效率,研究人员已开展了大量的研究工作,如,为避免PHC阴阳极间隙闭合,提出了新的功率脉冲汇聚结构[22-23];为减少电流损失,提出了对现有PHC的结构进行优化设计的方案[24]等。
上述工作对PHC电流损失机制的认识仍不够全面,通常认为阴极等离子体的产生和演化[25-33]导致PHC阴阳极间隙闭合,且它的扩散速度直接决定了阴阳极间隙闭合速度,但最新研究表明,PHC的阴阳极间隙闭合速度为35~ 50 cm·μs-1[18],远大于阴极等离子体扩散速度3~4 cm·μs-1[26-27]。阴极等离子体扩散机制非常复杂,扩散过程与理论预测相差甚远。其中,可能存在扩散速度远大于阴极等离子体整体扩散速度的其他粒子,加快了阴阳极间隙闭合过程。研究发现在MITLs工作过程中,阴极产生的等离子体中含有负离子,这些负离子在电场作用下可漂移到阳极[28-29],理论上可破坏传输线磁绝缘状态。但H-在兆伏每厘米的强电场作用下,漂移速度高达2 cm·ns-1[28-29],远大于实验结果[18, 26-27]。因此,在MITLs和PHC内部,负离子在强电磁场作用下的运动不是电场简单影响的结果。
另一方面,根据离子流的稳态磁绝缘理论[34],当Z装置上PHC电压为2 MV,负载电流为20~24 MA时,PHC附近磁场强度满足H-的磁绝缘要求,与PHC存在电流损失的现象相矛盾,表明PHC附近负离子的运动并不完全遵循稳态磁绝缘理论,与磁场的相互作用更加复杂。
因此,本文假设了一幅关于阴极等离子体运动的图像。在此图像中,负离子,尤其是H-,位于阴极等离子体前部,并以较快的速度先到达阳极。此时,阴阳极间隙闭合,且开始产生电流损失,但损失不大。随着后续阴极等离子体大量充斥在放电通道内,闭合的阴阳极间隙中放电通道电阻率随着等离子体的增加而快速下降,继而电流损失快速地变大直到峰值。在这幅图像内,可认为阴阳极间隙闭合过程(不是间隙完全短路或旁路)始于阴极等离子体(含负离子)的产生,终于负离子到达阳极。
根据实验获得的电流波形[36],定义PHC上游电流峰值10%的位置对应时刻为阴极等离子体和负离子产生的时刻;PHC上下游电流波形出现明显差异位置对应时刻为负离子到达阳极的时刻;负离子漂移时间为上述两者之差,间隙闭合速度为阴阳极间隙长度与负离子漂移时间的比值。
单孔PHC的粒子仿真模拟和“强光一号”加速器实验研究结果[34-35]给出阴极负离子流扩散速度与阴阳极间隙闭合速度相近,约为10 cm·μs-1。这表明阴极负离子和阴极等离子体的扩散现象之间存在联系与差别,阴极负离子扩散可能是PHC阴阳极间隙闭合一个重要原因,需深入探索研究。本文分析了阴极负离子流在强电磁场作用下的运动过程,且基于等离子体不稳定性的有效碰撞机制估算了负离子流的扩散速度。研究工作可为PHC的电流损失机制提供新的认识角度。
1 阴极负离子的运动
1.1 负离子产生机制
现有研究表明,负离子产生的根源是阴极表面的爆炸发射机制。吸附在阴极表面晶须附近的气体分子在爆炸发射过程中有很大概率形成负离子。
首先,爆炸发射会产生大量等离子体及中性分子。大量粒子在碰撞过程中,因共振机制而导致自身对称性遭到破坏的中性分子会在某些时刻呈电极性,碰撞截面也会增加[37-38]。因此,当电子与中性分子发生碰撞时,中性分子吸附一个电子而生成负离子的概率大大增加。
其次,爆炸发射产生的等离子体中带正电的离子,在电场作用下反向轰击阴极表面也能产生负离子[29]。Baker等[39]通过在与MITLs结构类似的实验平台上的研究工作,探明了反向散射的工作过程,验证了离子反向撞击阴极表面会产生负离子的物理机制。实验采用碱金属离子(Na+)以45°角撞击Mo金属表面,采用二次负离子质谱仪探测带电粒子的种类。当Na+的能量小于300 eV时,质谱仪探测到H-,O-,C-等负离子。实验证明,负离子的产额不仅与Na+离子的能量呈线性关系,且与Mo金属表面状态密切相关。随着Na+离子与金属膜的作用时间增加,Mo金属表面会生成一层Na金属膜。Mo金属表面覆盖的Na金属膜越厚,负离子的产额越大。实验表明,负离子电流随时间的变化率(dIs/dt)与注入碱金属离子流(Ip)的呈平方正比关系。
上述研究表明,MITLs阴极表面产生负离子是确定的物理事实。虽然负离子的产额相对较少且不稳定,但是Stinnett等[29]的实验结果表明,负离子电流密度与传输电流密度J3成正比[29,40]。因此,在大电流密度条件下,阴极负离子有可能使MITLs出现明显的电流损失。
1.2 等离子体内部的单粒子运动
为解释PHC间隙闭合的现象,需了解强电磁场环境下,PHC附近空间等离子体运动过程。通常情况下,等离子体默认为电中性并假设内部电场强度为0。然而,在动态的强磁场和强电场的背景下,MITLs或PHC阴极表面等离子体的某些运动机制,如带电粒子在不均匀磁场中的漂移和极化漂移会使等离子体内部带电粒子的分布呈特殊状态。
图1为径向MITLs的磁力线分布。由图1可见,在径向MITLs中,磁场呈同心圆状分布且越靠近中心,磁场强度越大。磁场沿径向存在磁场梯度且弯曲磁场线存在曲率。
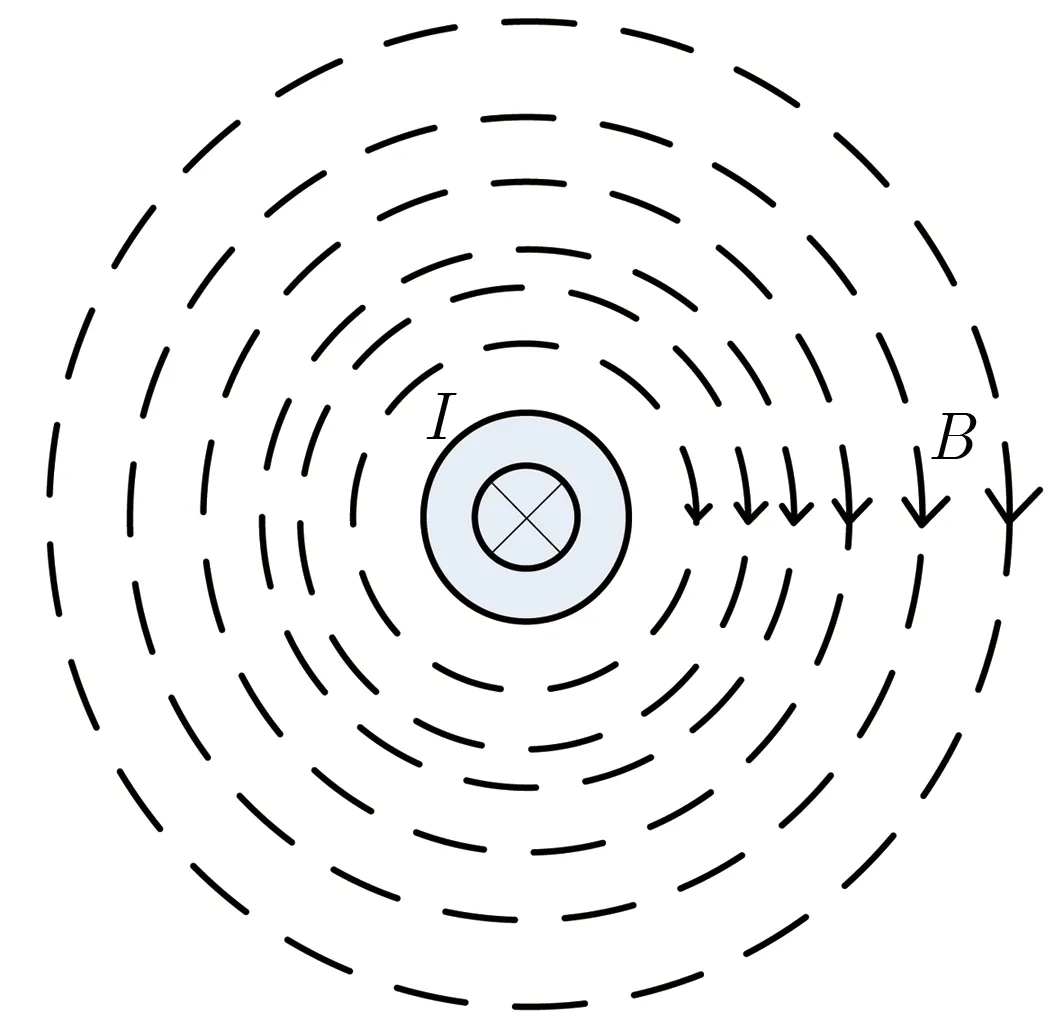
(a) r-θ direction
(b) r-z direction图1 径向MITLs的磁力线分布Fig.1 Magnetic field distribution of the radial MITLs
在这样的磁场下,带电粒子将做梯度漂移和曲率漂移,漂移速度可表示为[41]。
(1)
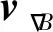
在实际运行条件下,驱动电压的幅值随时间快速变化。一般条件下,驱动电压的上升时间为百纳秒量级,主频约为107Hz,远小于MITLs阴阳极间隙中的电子回旋频率(约为1011Hz[42])。因此可认为,与电子回旋频率相比,电场强度随时间作缓慢变化。在此条件下,等离子体中的带电粒子沿电场方向的漂移,称为极化漂移[41],极化漂移速度可表示为
(2)
其中:vp为极化漂移速度;ωc为电子回旋频率;E为电场强度矢量。正极性和负极性粒子运动方向相反,分别向阴极和阳极漂移。
综上所述,在强电场、强磁场作用下,MITLs或PHC阴极附近的等离子体内部电荷的分布,如图2所示。电极表面覆盖的等离子体,整体呈现“准电中性”,但在上述的单粒子漂移机制作用下,等离子体靠近阴极一侧正电荷粒子偏多,靠近阳极一侧则负电荷粒子偏多。等离子体电荷的分布特性为进一步讨论正负离子在高频干扰电磁场作用下的运动提供了物理基础。

图2 在强电场、强磁场下阴极表面等离子体电荷分布Fig.2 Charge distribution characteristic of cathode plasma under the high electric and magnetic field
1.3 等离子体中的有效碰撞
当高功率脉冲传入PHC时,在其阴阳极间隙会产生大量的带电粒子和中性气体分子,并高速相互碰撞。在PHC的阴阳间隙中的等离子体的温度通常为3 ~ 5 eV[18, 42]。由于等离子体温度较低,所以粒子之间双体碰撞的频率很小。同时,由于等离子体的不稳定性,阴阳极间隙中还存在高频电磁场和静电场扰动[42-49]。高频扰动的电磁场会进一步影响等离子体行为,引起显著的类似于碰撞的等离子体集体行为。这种有效碰撞频率远大于粒子间的双体碰撞。
根据上述等离子体特性,研究人员基于有效碰撞机制,建立了MITLs碰撞电子流解析模型[42]。该模型可推导出阳极电流、电子电流和MITLs流阻抗等参数的理论边界值。在该模型中,碰撞系数α定义为
(3)
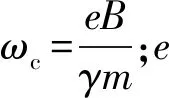
根据该稳态模型[42],由于高频电磁场扰动的影响,电子流存在一个向阳极方向运动的速度分量。有效碰撞是电子和高频扰动电磁场之间的相互作用,本文猜想离子与高频扰动电磁场之间也有相同的作用机制。根据该推论,将电子替换为负离子,分析负离子流对PHC阴阳间隙闭合的影响。
当电流密度较低时,MITLs的阴极负离子电流很小,很难影响到MITLs的传输效率[28-29]。但当MITLs的传导电流密度增大后,阴极负离子增多[40],需考虑阴极负离子对MITLs传输效率的影响。本文中,阴极负离子的有效碰撞系数可表示为
(4)
其中:ωi=eB/M为负离子回旋频率;M为氢离子质量;νi,eff为负离子有效碰撞频率,即负离子与高频扰动电磁场相互作用的碰撞频率。当负离子有效碰撞频率νi,eff和负离子回旋频率ωi相近时,负离子的有效碰撞效果更加明显。氢离子质量远大于电子质量,与电子的运动相比,在一般分析中通常假定氢离子处于相对静止状态。高频电磁场和静电场的扰动也作用于氢离子,与电子相比,这种作用机制会对氢离子产生影响,但肯定不如电子明显。在后文的论述中,也证明了这一点。
基于电子和离子同时与高频扰动电磁场进行相互作用的假设,可进一步假设两者的有效碰撞频率近似相等,即νi,eff≈νeff,可得
(5)
实际上有效碰撞频率远小于电子回旋频率,一般设α为0.1[42]。当电压为2 MV(γ约为5)时,代入氢离子和电子质量,可得αi约为37.3。表明,H-有效碰撞频率远大于自身的回旋频率。在此基础上,通过解析关于H-的磁流体运动方程,可判断H-的运动能否对阴阳极间隙闭合产生较为明显的影响。
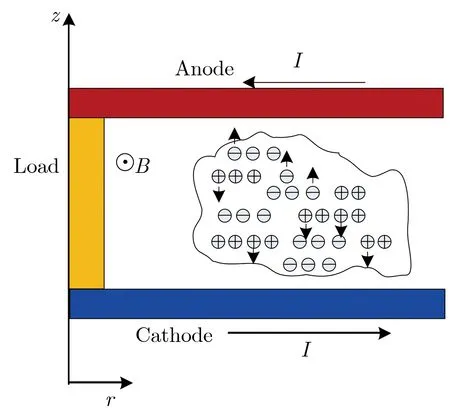
1.4 阴极负离子流磁流体力学方程
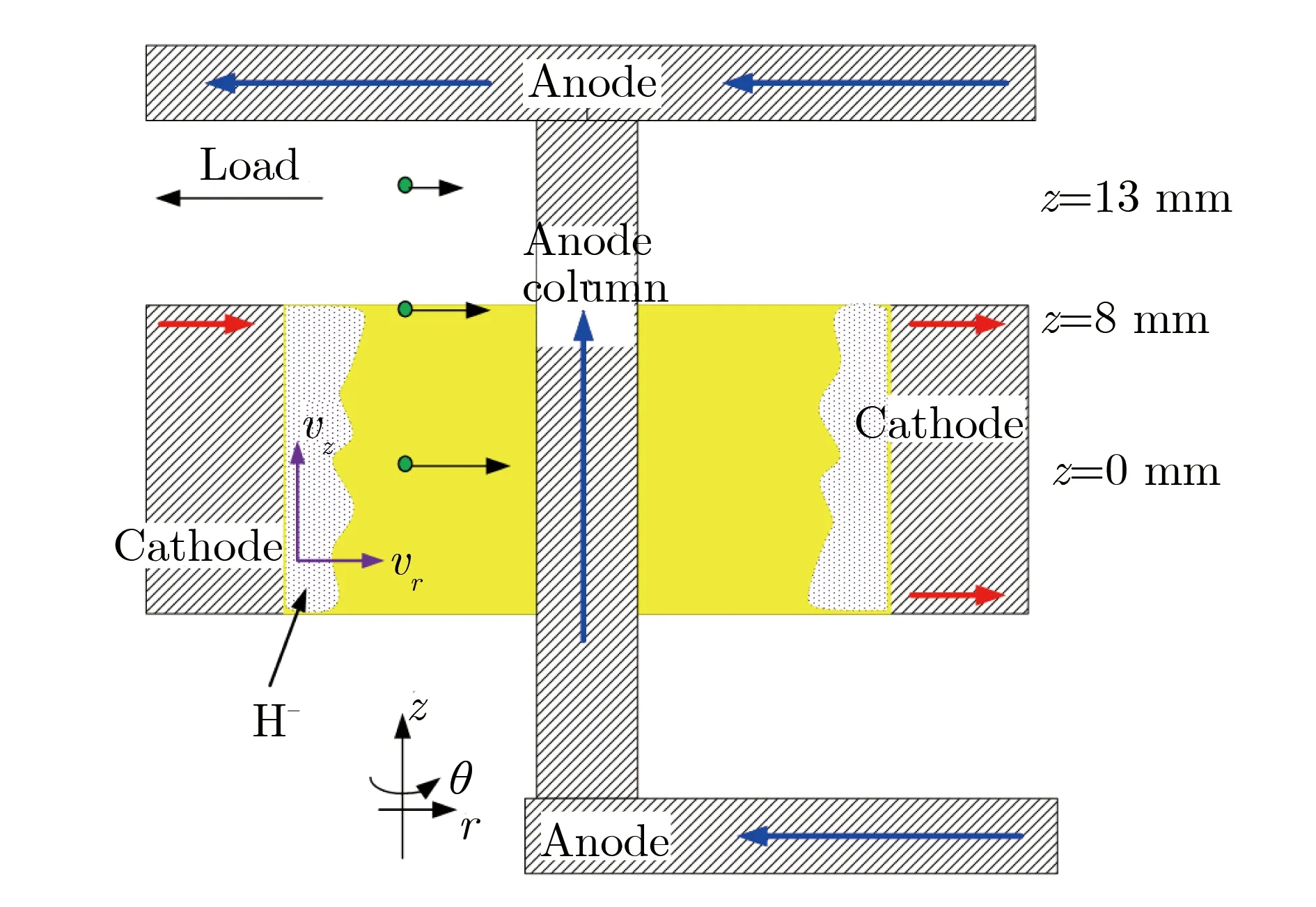
实验中,相继在MITLs和PHC的阴阳极间隙中发现H-, C-和O-等负离子[25, 28-29]。本文主要分析有效碰撞机制下阴极等离子体边缘存在的H-流的运动特点。图3为一段平板径向传输线的结构,采用圆柱坐标系。假设:(1)传输线阴阳极间隙只存在电子时,传输线满足磁绝缘状态;(2)鞘层不稳定性能使负离子流演化至扰动稳态;(3)等离子体扰动产生静电场和电磁场高频扰动,引起负离子发生有效碰撞;(4)阴极负离子可看作流体;(5)在流体模型中,高频扰动的效果可用带有效碰撞频率的碰撞项表示。
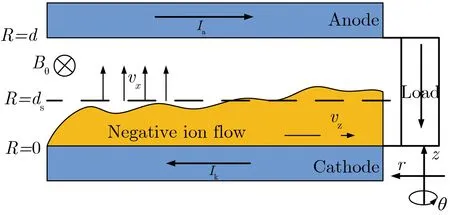
图3 平板径向传输线结构Fig.3 Configuration of the planar radial transmission line
图1中,功率流方向沿半径r反方向,电场沿z轴反方向,磁场方向为θ轴负方向。含碰撞项的流体方程可表示为
(6)
v·B=0
(7)
其中:nH为H-密度,小于电子密度和正离子密度;v为H-速度;E为电场强度;k为波尔兹曼常数;T为H-温度,数值与阴极等离子体温度相近。式(6)是动量守恒方程,假设H-压力张量各项同性。式(7)磁场方向与负离子流运动方向垂直。在磁绝缘环境下,可忽略密度梯度引起的扩散[42]。
式(6)和式(7)中,有效碰撞系数应为正。为计算方便,B用绝对值|B|代替。当阴极H-流处于稳态时,根据式(4)和式(5),可得
Er+vθBz-vzBθ=-αivr|B|
(8)
Eθ+vzBr-vrBz=-αivθ|B|
(9)
Ez+vrBθ-vθBr=-αivz|B|
(10)
vrBr+vθBθ+vzBz=0
(11)
联解等式(8)-式(11),可推得H-流在r,θ,z方向上的漂移速度,分别为
(12)
(13)
(14)
其中,A=αi|B|。由式(12)-式(14)可知,由于有效碰撞机制,H-流在3个方向上都有漂移可能。对于图3展示的理想径向传输线,仅分别在θ和z方向上有磁场和电场分量Bθ和Ez,因此,式(12)-式(14)可简化为
(15)
vθ=0
(16)
(17)
由式(15)-式(17)可知,αi≫1时,vz≫vr。表明,H-流主要向阳极扩散,可忽略其在径向方向的运动,这与有效碰撞机制下电子流运动的[42]特点不同;同时,H-流向阳极扩散的原因是等离子体不稳定性引发的高频电磁场扰动,而非磁感应强度弱,不足以偏转H-。
当用电子有效碰撞系数α代替H-有效碰撞系数αi时,式(15)和式(17)分别变为
(18)
(19)
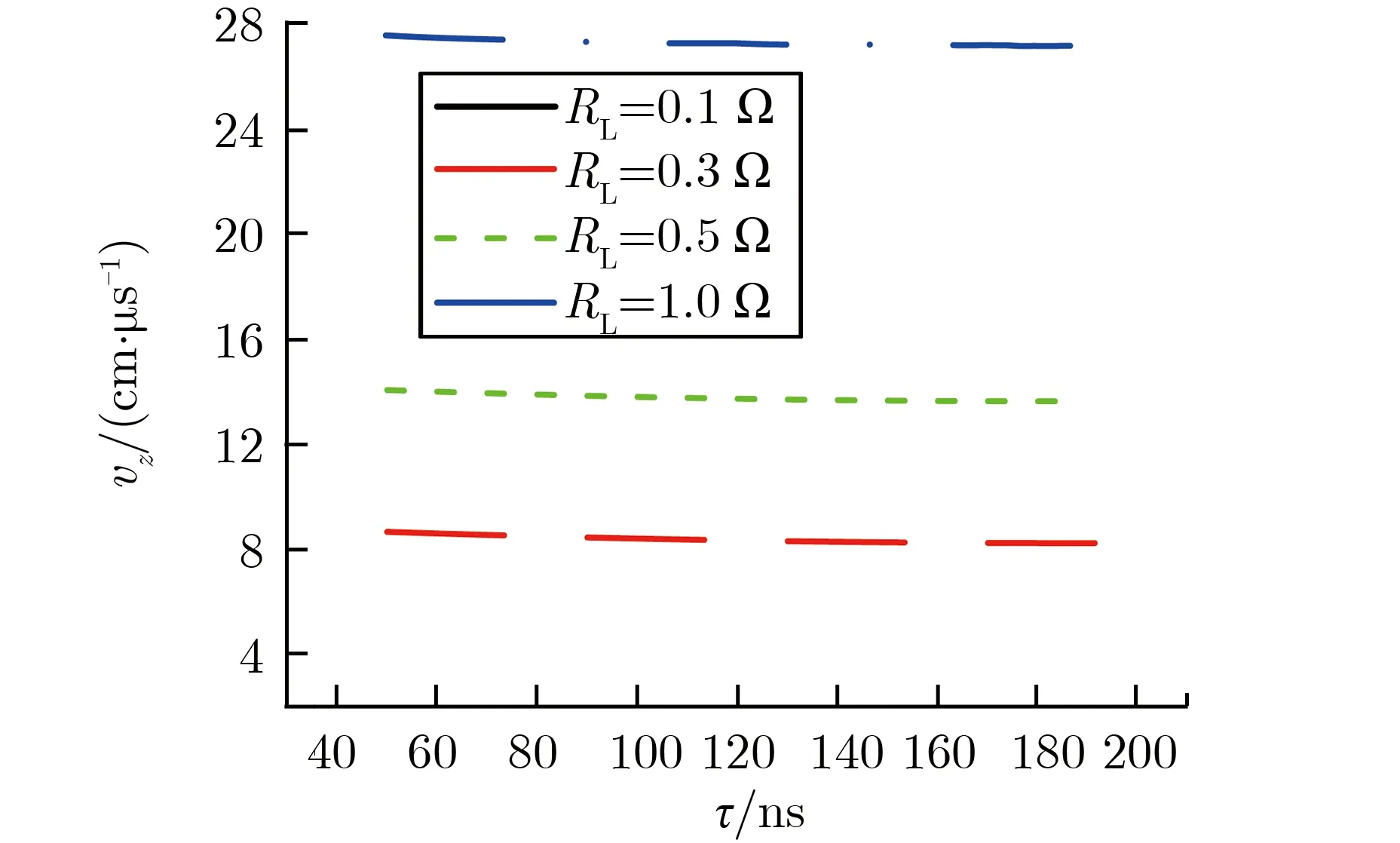
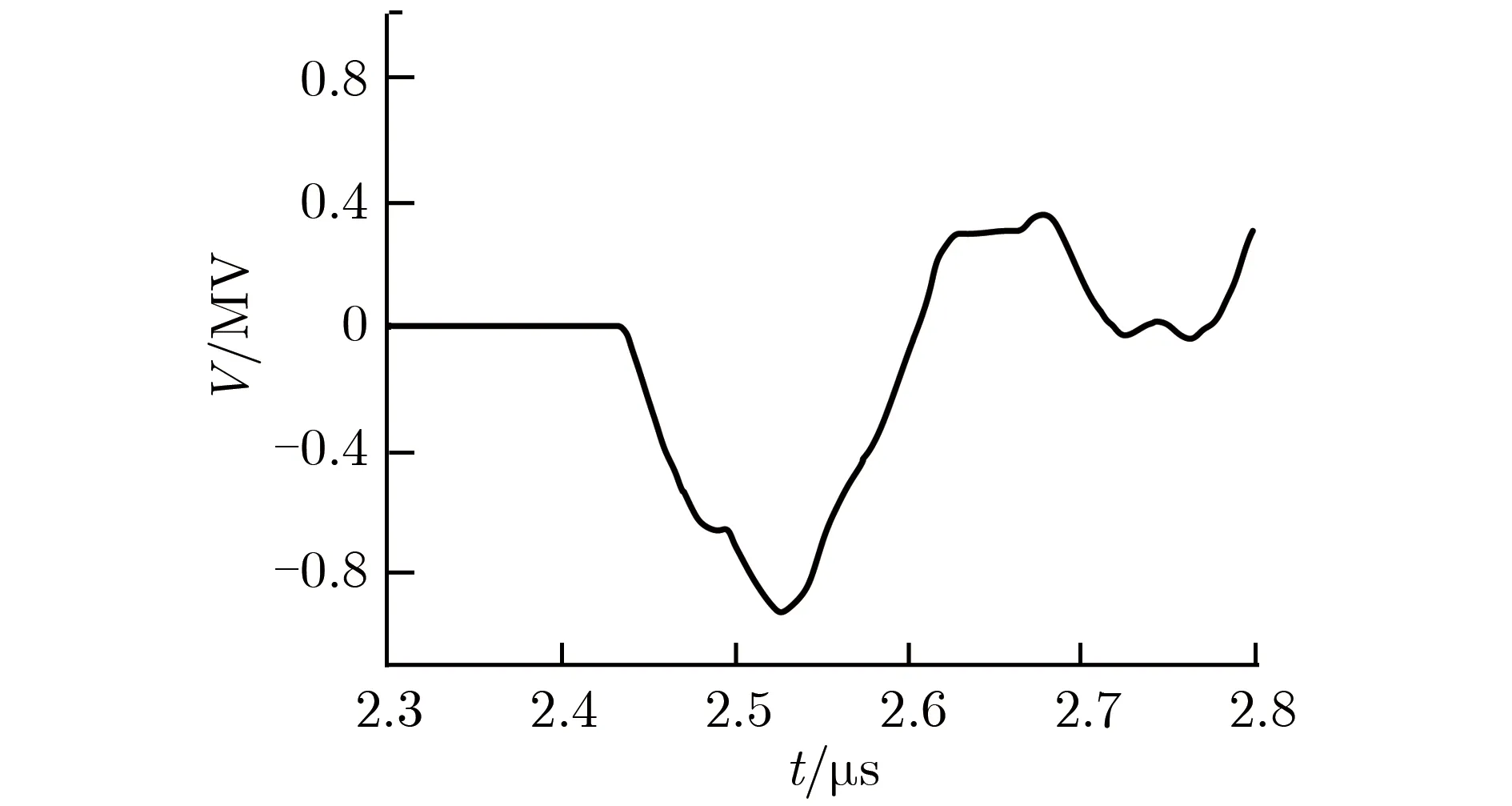
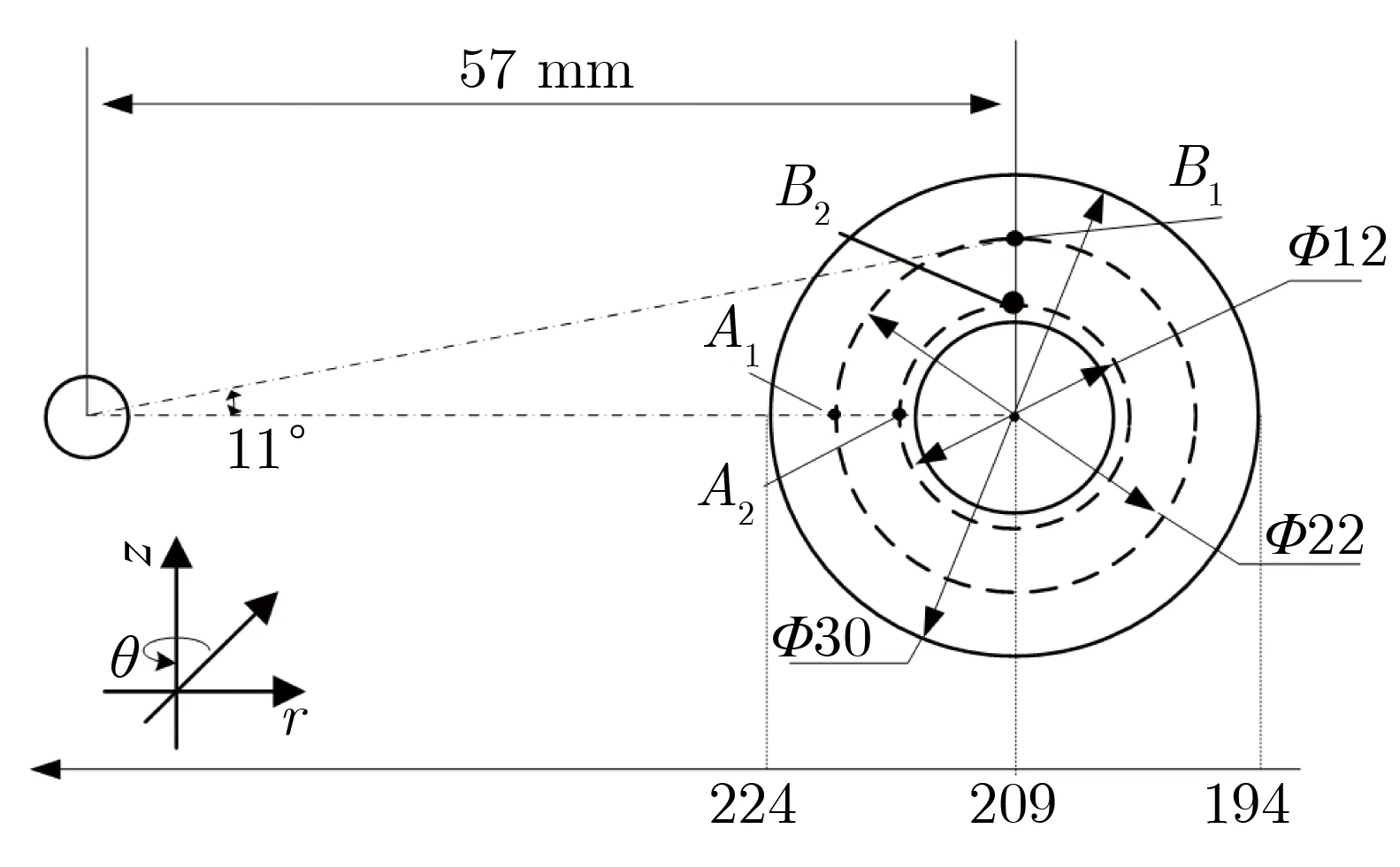
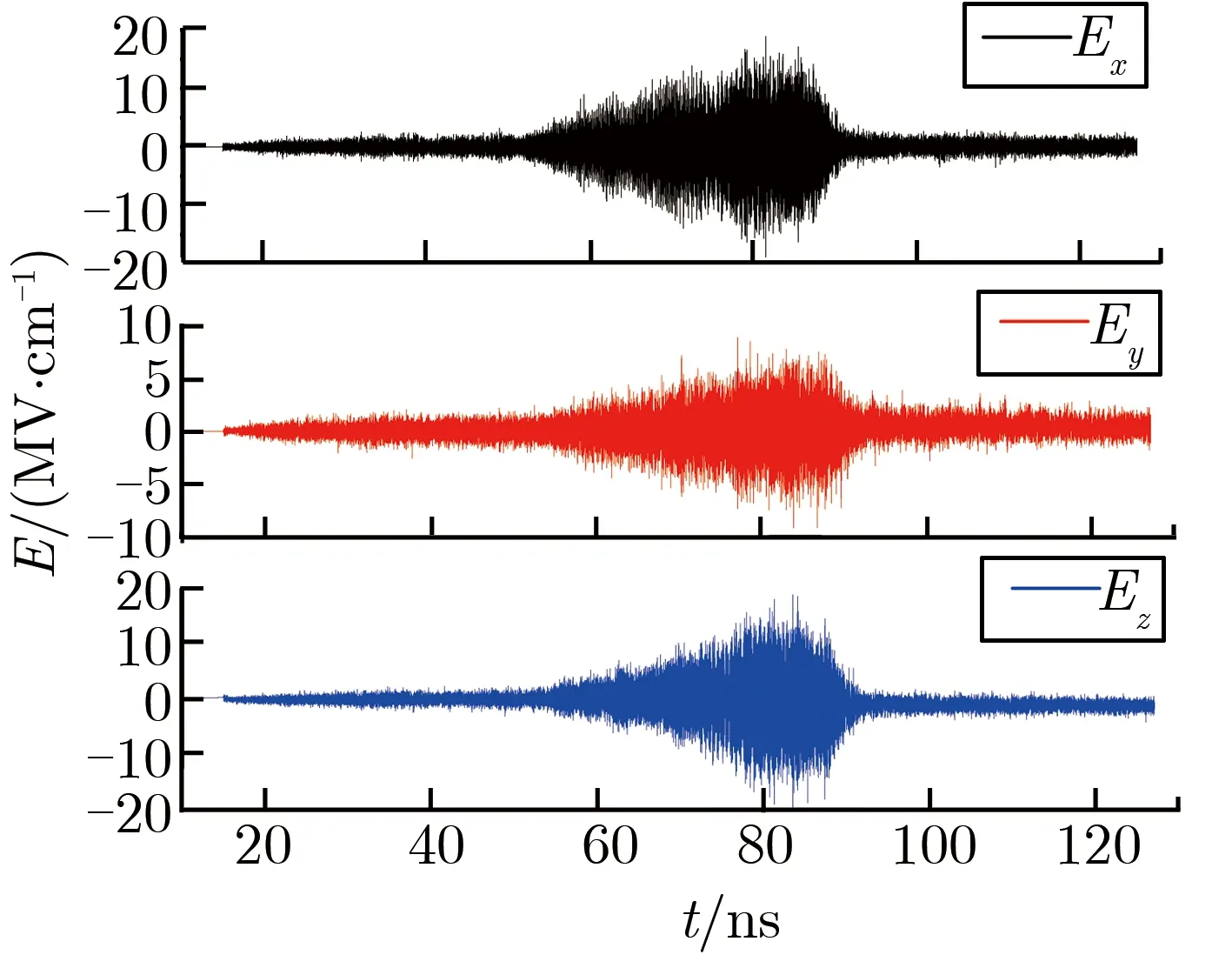
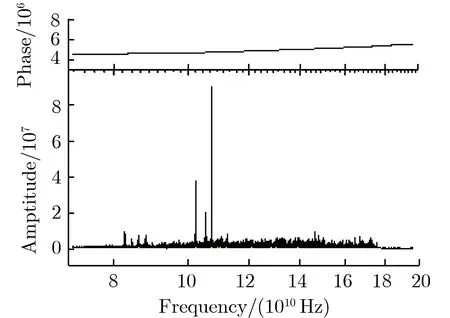
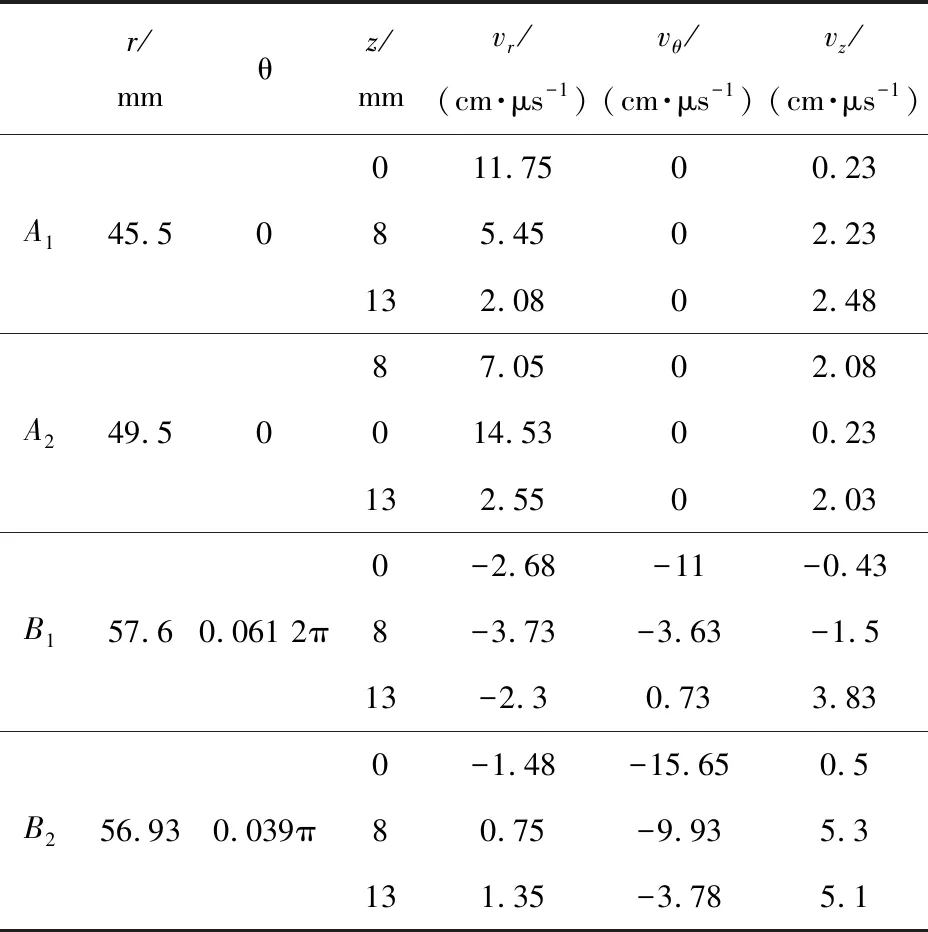
因α≪1,由式(18)和式(19)可知,电子流主要沿径向运动,仅有少量向阳极扩散。当电压为2 MV,α约为0.1时[42],根据式(4)得到1/αi约为0.027。此时,比较式(17)和式(19),有vz 为进一步讨论对H-流扩散的影响因素,可带入理想径向传输线的电场强度和磁感应强度Ez(r)和Bθ(r),式(17)可写为 (20) 其中:μ0为真空磁导率;V和L分别为传输线距离负载中心r处的电压和电感;d为阴阳极间隙;RL为负载阻抗。 dI/dt项可简化为I/τ,用于观察电流随时间变化的平均速率,τ为电流的上升时间(0~100%)。 (21) 当r为5 cm时,不同负载阻抗条件下,H-流的扩散速度随电压和电流上升时间的变化关系如图4所示。由图4可见,H-流扩散速度随负载阻抗增加而显著增加;由图4(a)可见,当r为5 cm,τ为50 ns时,H-流扩散速度随电压增加线性增加;由图4(b)可见,当r为5 cm,V为0.5 MV时,H-流扩散速度随电流上升时间增加而几乎无变化,表明,电流上升时间对H-流扩散速度的影响不明显。由此可知,H-流扩散速度对负载阻抗和工作电压的变化最为敏感。 (a) vz vs. V at τ=50 ns (b) vz vs. τ at V=0.5 MV 图4 当r为5 cm时,不同负载阻抗条件下,H-流的扩散速度随电压和电流上升时间的变化关系Fig.4 vz vs. V and vz vs. τ when r=5 cm with different RL PHC作为一段特殊的MITLs,电磁场分布远复杂于一般的MITLs。因此,需了解PHC附近电磁场分布,并根据式(12)-式(14),对PHC附近阴极负离子的扩散速度进行定性分析。 图5为用于电磁场仿真的单孔PHC模型。三板传输线阴阳极间距为10 mm,阳极柱穿过阴极孔连接传输线上下阳极板。三板传输线阴阳极平直部分长度分别为200,164 mm,短路负载直径为20 mm。 图5 单孔PHC模型Fig.5 Model of single-hole PHC 电磁场仿真时,通过“强光一号”加速器电路模拟得到的单孔PHC驱动电压V随时间t的变化关系如图6所示[50]。驱动源阻抗设为0.75 Ω,等效“强光一号”加速器的输出阻抗。驱动电压脉冲宽度大于单孔PHC电长度,因此可认为仿真过程处于准稳态。 图6 单孔PHC驱动电压V随时间t的变化关系Fig.6 V vs. t of single-hole PHC 仿真中,系统坐标系默认为直角坐标系,为计算方便,需将电磁场数据转换为柱坐标系。图7为单孔PHC结构中测试点的位置。通过获得不同位置的电磁场,可认识阴极负离子流的扩散运动特性。图7(a)为z=8 mm的平面上测试点的相对位置,分别在阴极孔与阳极柱之间不同位置选择A1,A2,B1,B24个测量位置。图7(b)为θ为0时的剖面上不同高度的测试点位置,即在上述每个位置上,分别获取z为0,8,13 mm时3个点的电磁场分布信息。 不同位置测试点的电场和磁场强度峰值如表1所列。由表1可知,在位置A1和A2处,在θ方向有磁场而电场强度为0。在位置B1和B2处,电磁场分布则比A1和A2处复杂。 (a) Vertical view, z=0 (b) Side view θ=0图7 单孔PHC结构中测试点的位置Fig.7 Test points of single hole PHC 表1 仿真得到的测试点电磁场强度峰值Tab.1 Peak values of the electric and magnetic field strength at test positions 将表1数据带入等式(12)-式(14),可估算阴极H-流的扩散速度。有效碰撞系数α可通过粒子仿真结果[35]进行估算。通过粒子仿真[35]可获得单孔PHC附近叠加了高频扰动的电场,如图8所示。图8(a)为电场强度3个方向上的分量,波形相似,峰值高达20 MV·cm-1。图8(b)为经傅里叶变换后,电场Ex波形的频谱特征。 (a) High frequency disturbing electric field (b) Spectrum characteristics at the single-hole PHC图8 单孔PHC附近叠加了高频扰动的电场Fig.8 High frequency disturbing electric field at the single-hole PHC 由图8(b)可见,电场Ex的频率范围为8×1010~2×1011Hz,主要集中在1011Hz附近。仿真设置最小时间步长为1.3 ps,频率约为1012Hz,远大于电场频率。基于此事实,一般可认为PIC仿真结果可信[51-52]。由于高频扰动电场与H-相互作用导致有效碰撞的发生,可近似认为有效碰撞频率约等于高频扰动电场频率。 文献[35]中,单孔PHC传输电流峰值约为1 MA,PHC附近磁感应强度约为32 T。PHC附近电压约为500 kV,电子的相对论因子γ约为2,可知电子回旋频率约为2.8×1012Hz,离子回旋频率约为1.5×109Hz。根据式(3)-式(4),可得有效碰撞系数α和αi分别约为0.04和66.7。 根据表1的电磁场数据和估算得到的有效碰撞系数α,结合式(12)-式(14),可得到α为0.04时,阴极H-流的扩散速度,如表2所列。由表2可知:当z=0时,在测试位置A1和A2处,阴极负离子流扩散速度主要含r方向的速度分量,且大于10 cm·μs-1;随着z的增加,扩散速度包含了r和z方向的速度分量,且大小相近,表明,在阴极孔边缘及其外部的阴极H-流扩散更为复杂;当θ=0时,阴极孔内H-流r方向的扩散速度vr为5.45~14.53 cm·μs-1;测试位置B1和B2处H-流的扩散速度除含有r和z方向的速度分量,还具有θ方向的分量。这个结果表明,其他位置(θ≠0)的H-会向单孔PHC下游处θ=0的截面聚集,并大大提高间隙击穿的概率。 表2 当α约为0.04时,H-的扩散速度Tab.2 The diffusion velocity of H- flow when α≈0.04 粒子仿真结果已表明:阴极H-在单孔PHC阴阳极间隙中的扩散速度约为10 cm·μs-1[35],同时“强光一号”加速器上单孔PHC电流传输效率实验结果表明PHC阴阳极间隙闭合速度为5.74~14.52 cm·μs-1[36]。由表2可知,理论计算结果与仿真和实验结果量级相近。数据之间差别的原因为:(1)表2中的速度大小根据具体位置上的电磁场强度计算得到,与平均扩散速度有所差别,但涵盖了平均扩散速度,且与之相近;(2)仿真获得的阴极H-扩散速度是其边缘平均扩散速度,仅反映阴极H-扩散过程的整体情况;(3)实验获得的单孔PHC阴阳极间隙闭合速度来自于18次实验数据。由于实际安装等工程因素和加速器本身输出电压存在的偏差导致阴阳极间隙闭合速度存在一定偏差;(4)计算过程中,本文电磁场仿真并未考虑等离子体的影响,空间点的电磁场数据存在一定偏差。通过理论估算、PIC仿真和实验获得的阴极H-扩散速度大小相近,表明阴极H-流的扩散在单孔PHC的阴阳极间隙闭合过程中,发挥了重要作用。 本文提出了等离子体的有效碰撞频率大小与高频扰动电磁场的频率近似的理论假设,建立了阴极H-流的有效碰撞的运动方程,并获得了阴极H-流的扩散速度表达式,分析了扩散速度和电压、传输线结构及负载阻抗的关系。 对单孔PHC进行了电磁场仿真研究,获得了阴极孔附近电磁场分布特征。通过对高频扰动电场的监测,计算了电子和H-的有效碰撞系数。进一步利用阴极H-流的有效碰撞运动等式,计算得到了单孔PHC附近典型位置上阴极H-流的扩散速度,为5.45~14.53 cm·μs-1。理论计算结果与PIC仿真和实验数据相近,表明,基于本文提出的理论假设而建立的阴极H-流有效碰撞概念可帮助理解PHC阴阳间隙闭合的物理现象。 本文研究仍存在需继续研究的物理问题,如从更基础的物理机制上解释离子流的有效碰撞机制及如何更合理地获取有效碰撞频率等问题。未来将继续开展研究工作,进一步深入研究PHC及MITLs电流损失的物理问题。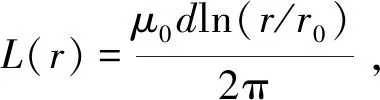
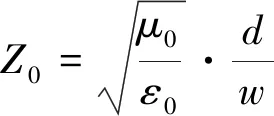

2 电磁场仿真及讨论
2.1 电磁场仿真
2.2 H-扩散

3 结论

