邓肯-张模型在寒区非饱和土中的应用

胡淑旗 訾亚丹

(河北建筑工程学院，河北 张家口 075000)

0 引 言

作为典型的季节性冻土区，冀北地区冬季寒冷，夏季炎热，冻融循环会改变土体的内部结构而影响土体的强度.同时，该地区路基边坡土体又常年处于高吸力非饱和状态，在冻融循环与吸力的双重影响下，极易发生路基边坡的浅层滑坡，威胁公路的正常运营.因此有必要对张家口非饱和土进行不同冻融循环次数下的力学特性研究.

抗剪强度是决定边坡稳定性的直接参数[1].大量学者已经就吸力、冻融循环次数对抗剪强度的影响进行了研究.董晓宏[2]对陕西黄土进行了不同冻融循环次数下的直剪试验，发现：抗剪强度随冻融次数的增加先减小后趋于稳定.一般强度在3～5次就可以降到最低.高登辉[3]通过三轴试验对重塑非饱和黄土进行了研究，发现吸力越大，试样的剪胀性越显著，强度越高.为了进一步分析，吸力与冻融循环对土体物理性质的影响，部分学者对土体抗剪强度指标：粘聚力和内摩擦角进行了研究.姜彤[4]利用直剪试验和三轴试验对非饱和膨胀土进行了研究，对比两种试验方法所得到的粘聚力和内摩擦角的变化规律，发现二者结果具有一致性，即黏聚力随基质吸力的增加而增加，内摩擦角随基质吸力的增加而有所减小.赵鲁庆[5]对冻融循环作用对土体的影响做了微观解释：冻融循环会破坏原状土颗粒间固有较强的胶结联结，土中水产生的冻胀力和迁移力也会不断减弱土颗粒间的胶结力，造成粘聚力减小，随着冻融循环次数的增加，土颗粒逐渐形成新的稳定结构，冻融循环作用对胶结力的削弱逐渐降低，粘聚力变化减小.

由于冻融循环试验和吸力控制试验需要耗费大量的时间和精力，学者们开始探究如何利用有限的数据挖掘大量的信息.建立正确的本构模型是方法之一.邓肯-张模型具有物理意义明确、可通过常规三轴试验简单获取的特点，在岩土工程中得到广泛应用.孙谷雨[6]对南京冻结粉质黏土进行了邓肯-张模型参数试验研究，得到的强度实测值和预测值吻合较好，说明了模型的可靠性.罗崇亮[7]基于三轴试验对红层泥岩的邓肯-张模型参数进行了研究，得到对不同含水率下的n值和K值实测值与计算值相关性良好.

邓肯-张模型普遍适用于饱和扰动土和砂土，对于非饱和土的适用性值得研究.为此本文以高吸力非饱和粉质黏土为研究对象，通过大量非饱和土三轴试验，得到不同冻融循环次数、吸力条件下的邓肯-张模型参数，通过对有限的参数进行分析研究，探究考虑吸力和冻融循环次数影响的非饱和土的切线变形模量的表达式，尝试利用邓肯-张模型来预测非饱和土的应力-应变曲线的峰前部分，以便得到土体抗剪强度，为寒区非饱和土边坡高次冻融循环和宽广吸力条件下的稳定性提供理论判据.

1 试验材料与试验方案

1.1 试验材料

试验土样取自于张家口延崇高速公路路基施工场地，依据JTG 3430-2020《公路土工试验规程》、GB/T 50123-2019《土工试验方法标准》[8-9]对土样进行颗粒分析、液限塑限以及击实试验得到其基本物理性质如表1.

表1 试验土体基本物理指标

1.2 试验方案

试验过程严格遵循JTG 3430-2020《公路土工试验规程》三轴试验规程进行.采用直径39.1 mm,高80 mm的圆柱体试样，取最优含水率配置土样，依据最大干密度制备90%压实度的试样，为防止水分流失，试样制备完成后用保鲜膜包裹.冻融循环试验采用高低温交变箱，冻结、融化温度分别设定为-15 ℃和20 ℃，冻结与融化时间均为12 h，冻融循环次数取0次、1次、3次、5次、9次.吸力采用蒸汽平衡法控制，如图1所示，共设计5级吸力，依次为3.29、13.10、21.82、38.00、71.12 MPa.制备完成的试样依次进行冻融循环、蒸汽平衡后，进行三轴试验，每组3个试样，施加围压分别为40 kPa、60 kPa、80 kPa.

图1 吸力平衡过程

2 试验现象及结果分析

2.1 三轴剪切试验应力应变曲线

不同冻融循环次数及吸力条件下，通过三轴剪切试验得到应力-应变((σ1-σ3)-ε1)的曲线如图2所示.由图2可知：

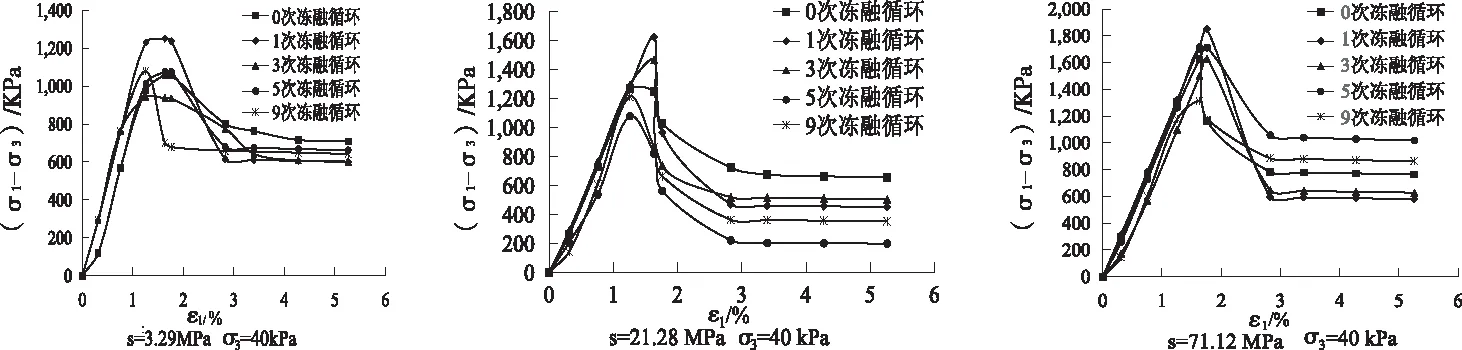
图2 不同围压粉质黏土应力-应变((σ1-σ3)-ε1)曲线

(1)吸力非饱和土的应力-应变((σ1-σ3)-ε1)的曲线均呈应变软化型.这是因为高吸力条件下土样含水率低，脆性大，达到峰值强度后土样破坏，强度开始下降.

(2)相同围压条件下，在加载初期，随着应力的增大，应变增长缓慢，应力-应变曲线近似下凸型，类似于岩体的压密阶段；在应变达到0.5%左右以后应变随应力近似线性增大，3.29 MPa吸力时，在达到峰值强度之前，出现应力增长缓慢而应变快速增大现象.

2.2 吸力、冻融循环次数对三轴抗剪强度的影响

以40 kPa围压下抗剪强度为例，图3(a)可知在围压一定时，相同冻融循环次数下粉质黏土抗剪强度随吸力的增大而增大，呈近似对数型增长.其主要原因是非饱和土中含水量随着吸力的增大而减少，促使土颗粒间表观粘聚力的升高，不易产生滑动，进而提高了非饱和土的抗剪强度.

由图3(b)可知在围压一定时，同种吸力条件下粉质黏土抗剪强度随冻融循环次数的增加表现为:先增大后减小最终趋于稳定.主要原因是：首次冻融循环作用破坏了试样的初始胶结，土颗粒重新排列的过程中增加了颗粒间的接触点，提高了摩擦力，进而短暂提高了抗剪强度；随着冻融循环次数的增加，土颗粒逐渐形成新的稳定结构，冻融循环作用对胶结力的削弱逐渐降低，对强度的影响减小[5].

图3 抗剪强度随吸力、冻融循环次数变化的曲线

2.3 不同冻融循环次数、吸力条件下抗剪强度指标

根据三轴试验数据，通过绘制莫尔圆得到不同冻融循环次数、吸力条件下抗剪强度指标粘聚力c、内摩擦角φ的值，如表2所示.根据表2试验结果，对抗剪强度指标c进行拟合，得到抗剪强度指标c与吸力s的函数关系，如图4所示，二者近似呈线性关系，即满足如下关系式：

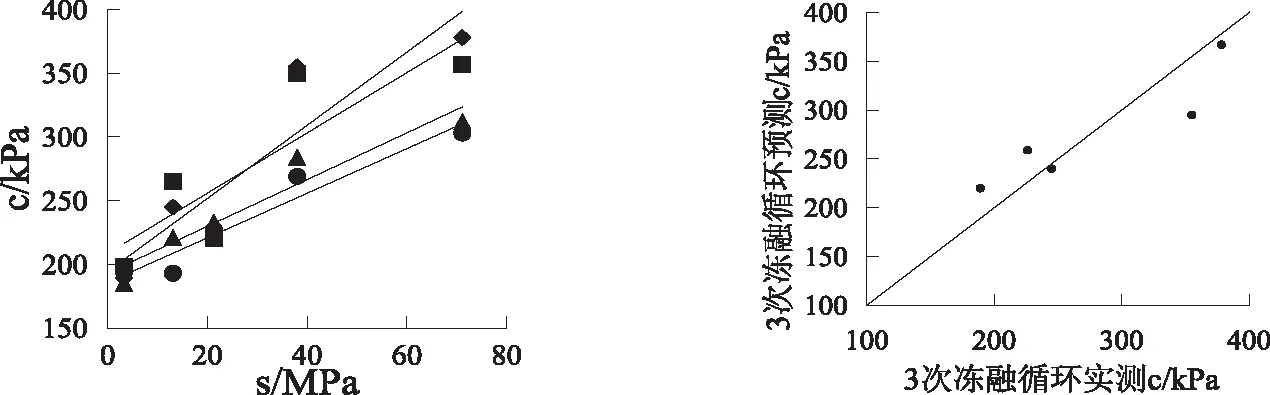
图4 s-c关系曲线 图5 3次冻融循环条件下实测值与预测值

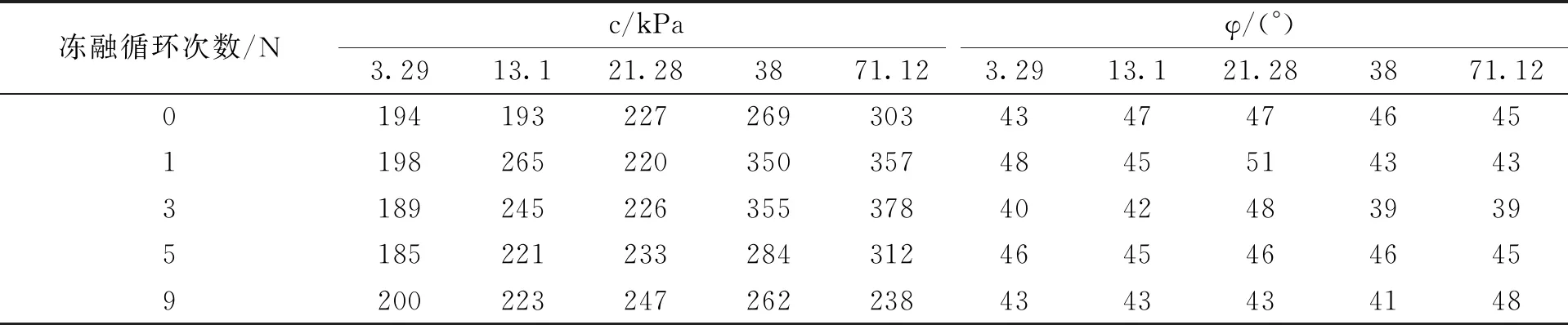
表2 不同冻融循环次数、吸力条件下c、φ值

c=A1s+B1

(1)

其中：A1、B1为吸力相关拟合参数,具体值见表3.

表3 不同冻融循环次数条件下吸力相关拟合参数A1、B1值

根据表3，对吸力相关拟合参数A1、B1进行拟合，得到吸力相关拟合参数A1、B1与冻融循环次数的函数关系，如下：

A1=-0.038 1N2+0.173 6N+1.993 1R2=0.935 8

(2)

B1=0.724 3N3-9.620 8N2+31.697N+185.8R2=1

(3)

根据式(1)-(3)可以预测3次冻融循环条件下，各级吸力对应的c值，结果如图5所示：预测值与实际值均匀分布在四十五度线附近，说明该预测公式有很好的适用性.

将表2中φ值试验结果处理，得到s/φ与s的关系，对二者进行拟合发现近似呈线性关系，如图6所示，拟合关系式如下：

s/φ=A2s+B2

(4)

其中：A2、B2为吸力相关拟合参数,具体值见表3.

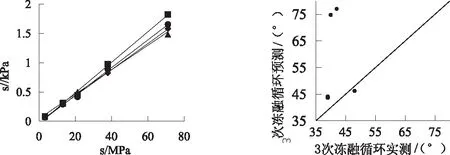
图6 s-s/φ关系曲线 图7 3次冻融循环条件下实测值与预测值

根据表3试验结果，对吸力相关拟合参数A2、B2进行拟合，得到吸力相关拟合参数A2、B2与冻融循环次数的函数关系，如下：

A2=0.000 04N3-0.000 6N2+0.001 8N+0.022 3R2=1

(5)

B2=-0.000 5N3+0.008 3N2-0.027 9N-0.010 7R2=1

(6)

根据式(1)-(3)可以预测3次冻融循环条件下，各级吸力对应的φ值，结果如图7所示：预测值与实际值均匀分布在四十五度线附近，说明该预测公式有很好的适用性.

3 邓肯-张模型的应用

3.1 不同冻融循环次数、吸力条件下模型参数K、n

拟合lg(Ei/Pa)与lg(σ3/Pa)得到的二者近似线性的关系，根据拟合关系式得到模型参数K、n的值，见表4：

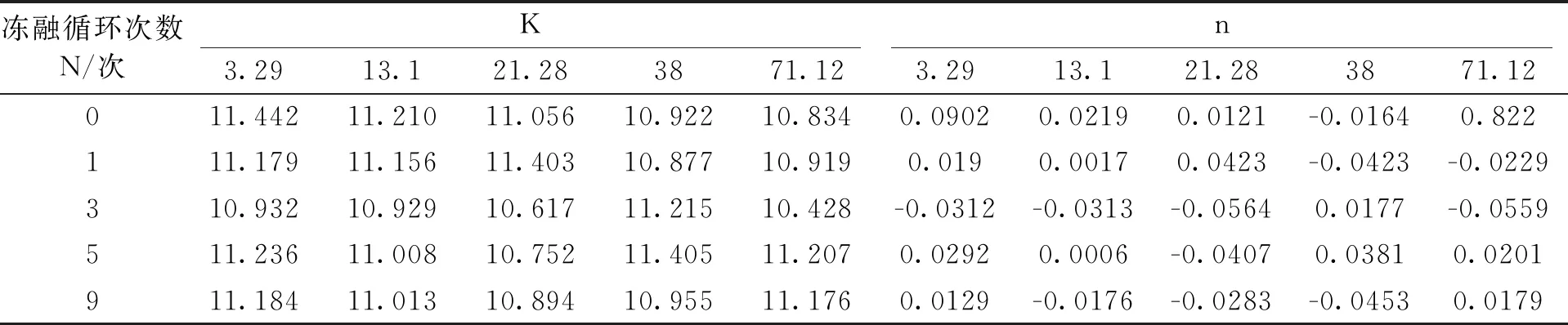
表4 不同冻融循环次数、吸力条件下模型参数K、n

lg(Ei/Pa)=lgK+nlg(σ3/Pa)

(7)

式中：Pa(=101.4)为大气压，kPa.

3.2 不同冻融循环次数、吸力条件下模型参数Rf

图1所示应力应变曲线为有峰值的情况，因此取(σ1-σ3)f=(σ1-σ3)峰[10]，则破环比为：

(8)

3.3 考虑冻融循环次数和吸力的切线变形模量

将参数c、φ带入式(9)可得

(9)

(10)

式(10)反映了冻融循环次数、吸力对对非饱和土切线模量的影响.

3.4 模型验证

为验证模型的可靠性，将试验值与计算出的邓肯-张模型数值进行对比，以围压40 kPa为例.邓肯张模型为非线性弹性模型，达到峰值以后，土样发生破坏，继续加载，其变形不再满足非线性弹性，因此，此处只研究峰值以前.由图8可知通过邓肯-张模型计算得到的应力-应变曲线与相同试验条件下试验得到的应力-应变曲线比较一致，因此本模型可用于预估不同吸力、不同冻融循环次数下应变软化型非饱和土的应力-应变曲线的峰前部分，为寒区非饱和土边坡高次冻融循环和宽广吸力条件下的稳定性提供理论判据.

图8 非饱和土应力-应变(σ1-σ1)-ε1曲线实测值与预测值对比

4 结 论

(1)高吸力非饱和土的应力-应变曲线均呈应变软化型；加载初期，随着应力的增大，应变增长缓慢，应力-应变曲线近似下凸型，类似于岩体的压密阶段；在应变达到0.5%左右以后应变随应力近似线性增大，3.29 MPa吸力时，在达到峰值强度之前，出现应力增长缓慢而应变快速增大现象.

(2)围压一定时，相同冻融循环次数下粉质黏土抗剪强度随吸力的增大而增大，近似对数型增长；同种吸力条件下粉质黏土抗剪强度随冻融循环次数的增加表现为:先增大后减小最终趋于稳定.

(3)对不同冻融循环次数、吸力条件下的抗剪强度指标c、φ拟合，得到二者关于冻融循环次数、吸力的拟合公式，用于预测不同冻融循环次数、吸力条件下的抗剪强度指标具有适用性.

(4)提出考虑吸力和冻融循环次数影响的非饱和土的切线变形模量的表达式，可用于预估不同吸力、不同冻融循环次数下应变软化型非饱和土的应力-应变曲线的峰前部分，为寒区非饱和土边坡高次冻融循环和宽广吸力条件下的稳定性提供理论判据.