eSQG 方法在南海垂向流速诊断中的应用研究

黄家辉，谢玲玲,，李强,，李敏,

(1.广东海洋大学 海洋与气象学院 近海海洋变化与灾害预警实验室，广东 湛江 524088；2.广东省高等学校陆架及深远海气候资源与环境重点实验室，广东 湛江 524088；3.自然资源部空间海洋遥感与应用重点实验室，北京 100081)

1 引言

垂向流速作为海水运动的一个重要分量，对海洋内部以及海气间的物质和能量交换具有重要作用。垂向运动能将深层富含营养盐的冷水向上层海洋输送[1–2]，从而提高海区的初级生产力[3–5]。同时，垂向运动也能将表层海洋溶解的氧气和二氧化碳带至深层[6–7]，影响全球的碳氧循环，加速深层海洋对气候的响应[8]。因此，获取垂向流速具有重要的研究意义和应用价值。

海洋垂向流速的量级一般只有10−6～10−3m/s，在当前技术下难以直接测量。因此，研究者一般通过间接估算、动力诊断或者数值模拟等方法来获取垂向流速[9–12]。其中，基于海面高度场的有效表面准地转（effective Surface Quasi-Geostrophy，eSQG）方法和基于温盐水平流场的Omega 方程是获取海洋三维垂向流速的有效途径[13–14]。尤其是eSQG 方法，具有计算效率高、对现场观测依赖小等优势[15]，近年来在大洋海区的中尺度垂向流速诊断方面开展较多应用[16]。

Lapeyre 和Klein[17]最早提出了eSQG 方法，并指出eSQG 能较好诊断500 m 深度以浅的垂向流速。后续在黑潮延伸体、北大西洋和北太平洋等大洋海区的研究中，eSQG 方法的有效性在混合层以深的上层海洋得到较好印证[18–21]。eSQG 在混合层垂向流速诊断的不足，可以通过加入湍流混合引起的垂向流速来解决[22–23]。eSQG 对于不同尺度垂向流速的诊断效果不一样，其主要适用于20～400 km 的中尺度垂向流速诊断[16]。前人研究多集中于大洋海域，关于eSQG 在边缘海的适用性还有待进一步探索。

南海是西太平洋最大的半封闭海盆，其地形多变、动力过程复杂，中尺度和次中尺度过程强盛[24–25]，海盆和陆架均存在活跃的垂向环流[26–27]。关于南海的垂向流速，前人多采用简单估算或数值模式给出结果[28–31]。基于海面观测的eSQG 方法可否为南海垂向环流三维结构和定量特征探究提供有效方法，该问题有待解答。

因此本文将利用高分辨率的OFES（ocean general circulation model for the earth simulator）数值模拟数据，分析eSQG 在南海不同区域垂向流速诊断的适用性，给出南海垂向流速的时空特征，并探究不同时空分辨率对诊断结果的影响。

2 数据与方法

2.1 数据来源

本研究所用数据为OFES 模式提供的高分辨率海洋模式资料，其水平分辨率为0.1°×0.1°，时间分辨率为3 d。数据来自夏威夷大学亚太数据研究中心（Asia Pacific Data Research Center，APDRC）。该模式是由美国国家海洋和大气管理局地球物理流体动力学实验室开发，通过日本海洋与地球科技研究所地球模拟器计算得到的高分辨率海洋模式。空间覆盖范围为75°S～75°N，时间范围为1950 年1 月至2017 年12 月，垂向上有54 层，相邻两层之间的垂向间隔随着深度的增加而增加，最小约为5 m，最大约为330 m。温盐和水平流速数据表层深度为2.5 m、底层深度为5 900 m，垂向流速数据表层深度为5 m、底层深度为6 065 m。地形资料来源于南安普顿海洋中心的海洋环流和气候进展模式（Ocean Circulation and Climate Advanced Modeling，OCCAM）计划测得的（1/30）°地形数据，并通过平滑处理至与真实地形非常相近。该模式的水平湍流扩散项采用双调和算子，从而减小动量方程中水平网格尺度的误差。垂直混合采用KPP（K–profile parameterization）边界层混合方案。该模式为冷启动，用NCEP/NCAR（National Centers for Environmental Prediction/National Center for Atmospheric Research）再分析数据作为大气强迫场，温盐资料则采用WOA（World Ocean Atlas）数据。

本文选取南海（4°～24°N，106°～122°E）2012 年3 月至2013 年2 月的OFES 模式位势温盐、流速、海面高度和混合层厚度进行分析。其中位势温度和盐度用于计算0～300 m 深度的浮力频率，海面高度用于诊断垂向流速，水平流速用于计算相对涡度，模式垂向流速用于与eSQG 诊断垂向流速对比。时间选取考虑与Qiu 等[18–19]的大洋结果进行对比。

2.2 eSQG 诊断方法

Lapeyre 和Klein[17]指出在斜压不稳定的情况下，海洋内部位势涡度异常与表层密度异常存在显著的相关关系。基于这一相关关系和位势涡度的可逆性，可以得到地转流函数 ψ在某一深度z与海面高度 η的表达式为

继而，可以根据地转方程、静力方程和平流的浮力方程推得浮力b和垂向流速w的表达式为

利用模式提供的SSH 数据 η (x,y)，由式（3）计算不同深度不同波长的垂向流速，继而通过傅里叶反变换，可得到不同深度的垂向流速分布。eSQG 诊断垂向流速记为ωeSQG，模式垂向流速记为ωOFES。以Qiu 等[18–19]研究的黑潮延伸体（31°～39°N，145°～153°E）为例，验证本研究eSQG 方法。可见，单日（2012 年3 月29 日）400 m 深度ωeSQG与ωOFES的水平分布特征基本一致，尤其是二者的中尺度特征吻合较好（图1a，图1b）。ωeSQG相比ωOFES较弱，这可能是因为ωOFES包含部分非地转过程。混合层以深两种垂向流速的相关系数rs基本在0.5 以上（图1c），表明eSQG 较好地再现了ωOFES。图1d 进一步给出了年平均rs剖面。年平均rs随深度的增加而增加并在混合层以深达到0.4 以上（图1d），说明eSQG 诊断结果在黑潮延伸体具有较好的稳定性。以上结果与Qiu 等[18–19]研究结果相似，证 明了本研究eSQG 方法的可行性。

图1 2012 年3 月29 日黑潮延伸体400 m 深度ωeSQG（a）和ωOFES（b）的水平分布，ωeSQG 和ωOFES 的空间相关系数rs 的垂向时间序列（c）以及年平均结果（d）Fig.1 Horizontal distribution of vertical velocity ωeSQG (a) and ωOFES (b) at 400 m in the Kuroshio Extension area on 29 March 2012,time series (c) and yearly average (d) of vertical profiles of spatial correlation coefficient rs between ωeSQG and ωOFES in the area

在南海垂向流速诊断中，由于陆地上不存在SSH，无法进行傅里叶变换。对靠近陆地边界时这一普遍问题，Isern-Fontanet 等[32]曾利用随距离衰减的权重函数对湾流海域的陆地进行赋值，以解决陆地上不存在SSH 的问题。本研究采用类似的二维线性插值对陆地区域赋值，进而傅里叶变换得到垂向流速，然后将陆地区域结果排除。同时，为了避免边界效应，将研究区域四周外扩2°后进行变换。

3 南海海盆垂向流速诊断结果

3.1 空间分布和季节变化

图2 示出4 种情况下南海100 m 深度ωeSQG、ωOFES和二者差值的水平分布。可见，相比年平均和季节平均，单日ωeSQG最强，其中台湾附近及其西南部ωeSQG的量值基本达到2×10−5m/s 以上（图2a）。年平均ωeSQG最弱，量值基本在1×10−5m/s 以下，尤其是东南部海域几乎全部小于0.5×10−5m/s（图2d）。夏季ωeSQG在台湾西南部较强，南海平均量值为1.6×10−5m/s（图2g）。冬季ωeSQG呈陆架边缘强，海盆内部较弱的特征，南海平均量值为9.5×10−6m/s（图2j）。综上，ωeSQG呈现北强南弱（以14°N 为界）、夏强冬弱的时空特征。

对比“真值”ωOFES（图2b，图2e，图2h 和图2k），ωOFES北强南弱的空间特征不明显，季节变化则为冬强夏弱。ωeSQG和ωOFES季节变化差异，可能与eSQG 主要适用于中尺度的垂向流速诊断有关[16,21]。前人分析显示南海中尺度过程具有ωeSQG类似的时空特征[33–34]，而南海次中尺度过程则冬强夏弱[26–27]。ωOFES包含部分次中尺度过程，次中尺度过程引起的垂向流速通常高于中尺度过程，因此呈现次中尺度过程的冬强夏弱特征。

图2 单日（2012 年5 月16 日，a−c）、年平均（d−f）、夏季（g−i）、冬季（j−l）南海100 m 深度ωeSQG、ωOFES 和二者差值的水平分布Fig.2 Horizontal distribution of ωeSQG,ωOFES and their difference at 100 m in the South China Sea on 16 May 2012 (a−c),in the whole year (d−f),summer (g−i) and winter (j−l)

图2c，图2f，图2i 和图2l 进一步给出了4 种情况下ωeSQG和ωOFES之差（记为ωminus）的水平分布。可见，单日ωminus的主要特征表现为涡丝结构，表明两种流速在次中尺度上的差异。南海南部的单日ωminus几乎全部为负值，反映了南海南部ωeSQG普遍弱于ωOFES的空间特征。年平均、夏季和冬季ωminus均以负值为主且在南海南部较大，反映了eSQG 在中尺度过程较弱海域诊断结果普遍偏低。值得注意的是，年平均、夏季和冬季ωminus在台湾西南部和越南以东普遍较小，这可能是因为南海中尺度过程在这两个区域最为强盛[33–34]。4 种情况下ωminus绝对值小于1 的占比分别为77%（单日）、95%（年平均）、87%（夏季）和94%（冬季），表明ωeSQG和ωOFES的量级基本相当。ωminus的高值主要集中在南海南部和陆架附近，表明eSQG 在这些区域的适用性较差。

计算南海全范围和深水区（水深大于1 000 m）ωeSQG与ωOFES的空间相关系数，分别记为和。单日（2012 年5 月16 日）和年平均的分别为0.14（p<0.01）和0.01（p=0.18），则分别达到0.34（p<0.01）和0.06（p<0.01）。夏季和冬季分别为–0.03（p<0.01）和0.02（p<0.01），而则分别为0.02（p<0.01）和0.17（p<0.01）。rs表现为单日rs最大，冬季rs大于年平均rs，夏季rs最小。普 遍大于表明eSQG 在南海深水区诊断效果优于浅水区。该结果低于在黑潮延伸体强涡旋区的单日对比相关系数（0.6～0.7）[18]，但与北太平洋区域研究结果相近（单日对比相关系数为0.4～0.5）[20]。这可能是3 个区域动力过程的差异引起的，进一步说明ωeSQG诊断方法在远离地形的深水区更有效。

3.2 不同深度和时间变化

图3 示出南海ωeSQG和ωOFES空间相关系数的垂向时间序列。可见，在冬季整体相对最大，春、秋季次之，夏季最小（图3a）。这是因为南海混合层深度在冬季最大、夏季最小，前人研究表明混合层深度增加能提高eSQG 诊断效果[32]。在混合层上下存在明显分层，混合层以浅相对混合层以深小。这一结果与Qiu 等[19]给出混合层以浅空间相关系数小于0.6，混合层以深空间相关系数为0.6～0.79 的研究结果相似。年平均结果显示（图3b），随深度的增加先增大后减小，在290 m 附近达到最大值0.11。对比深水区（图3c），随 时间和深度的变化趋势与相似，但是量值有所增大。最 大值为0.29，而最大达到0.38。这表明eSQG 更适用于南海深水区。年平均显 示（图3d），随着深度的增加先增大后减小，在120 m 附近达到最大值0.18。年平均达到最大值的深度要浅于年平均，这可能是受到样本数量变化的影响。

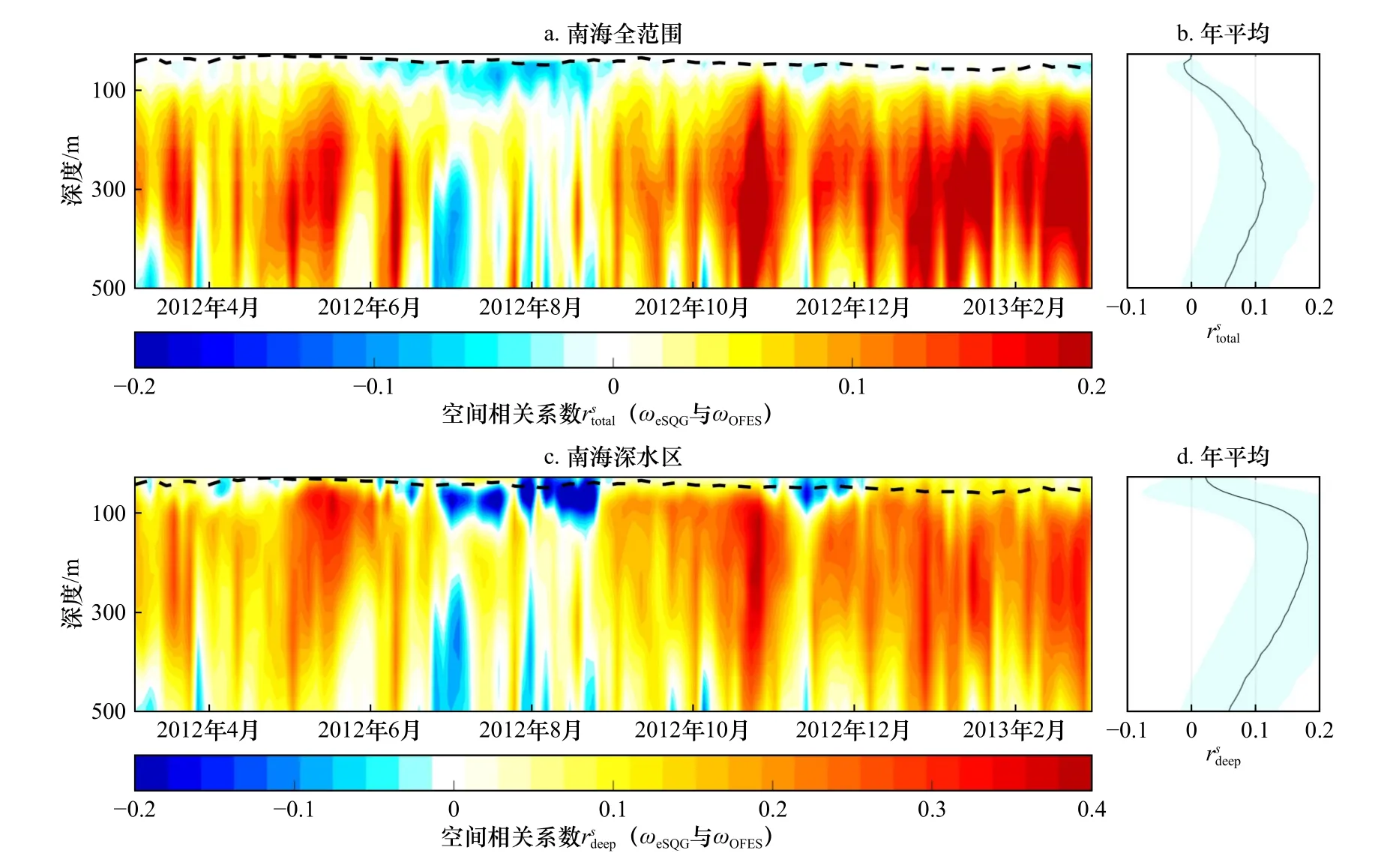
图3 南海全域和深水区ωeSQG 和ωOFES 的空间相关系数（a−b）和（c−d）的垂向时间序列及其年平均Fig.3 Time series and yearly average of vertical profiles of correlation coefficient and between ωeSQG and ωOFES in the whole South China Sea (a−b) and the deep basin (c−d)

图4 进一步给出了2012 年3 月至2013 年2 月南海50 m 和100 m 层各网格点上ωeSQG和ωOFES的时间相关系数rt的水平分布。从空间特征来看，rt在海盆西北部较高、东南部较低。台湾西南部、海南东南部和越南以东的rt普遍较高，这与南海海盆尺度的气旋式环流有较好的对应。对比图4a 和图4b 可知，两层时间相关系数rt的高值区的水平位置基本不变，100 m层rt普遍高于50 m 层。这说明rt在垂向上具有较好的连续性，eSQG 在同一区域不同深度的诊断效果具有一定的稳定性。台湾西南部和越南以东50 m 层rt普遍在0.4 以上，100 m 层更高达到0.5 以上。该结果进一步表明eSQG 在中尺度过程强盛的区域存在较好的适用性。rt在陆架浅海区普遍低于0.2，这可能与底边界对垂向流速的影响有关。

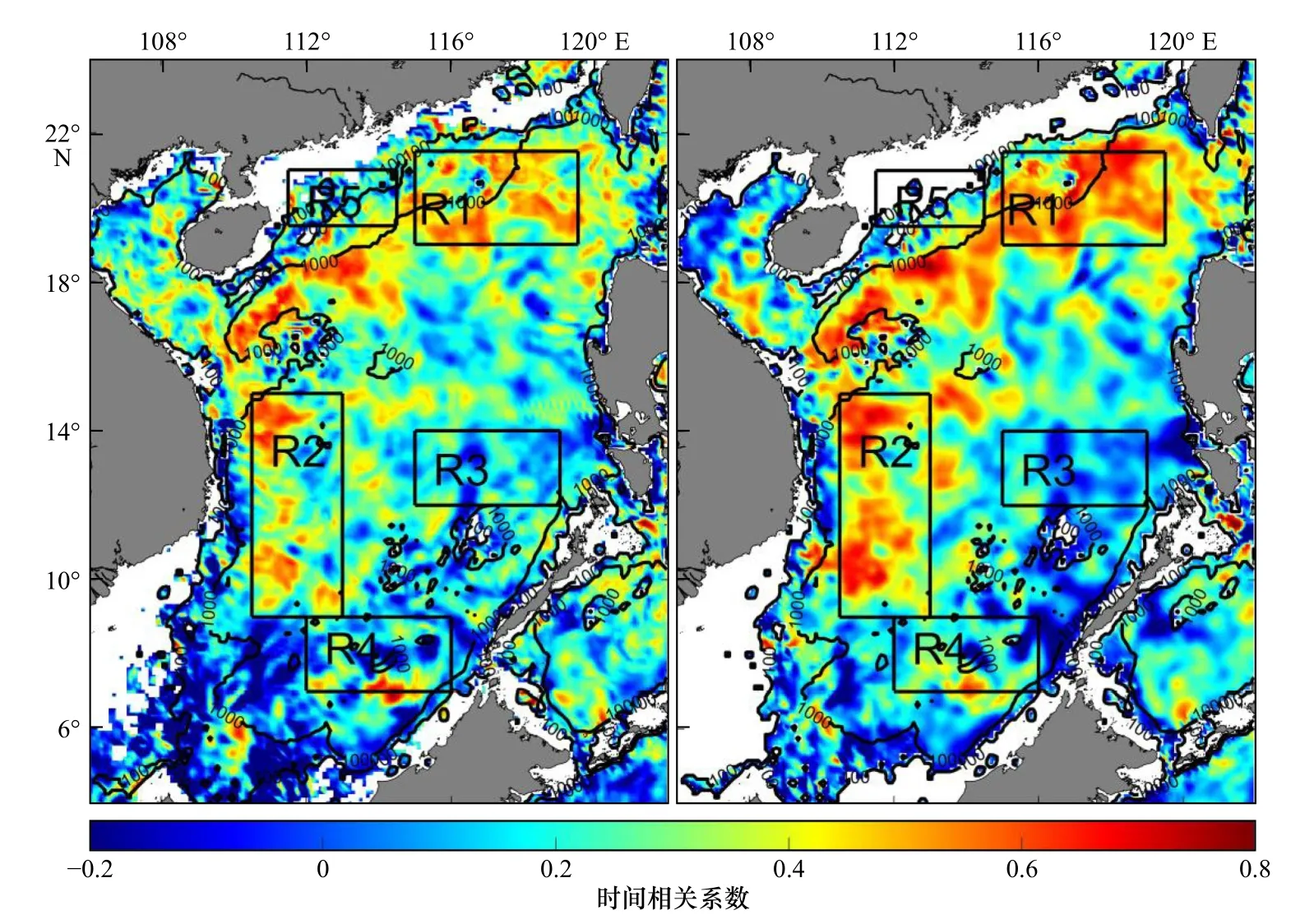
图4 南海50 m（a）和100 m（b）层各网格点上2012 年3 月至2013 年2 月ωeSQG 和ωOFES 的时间相关系数rt 的水平分布Fig.4 Horizontal distribution of temporal correlation rt between ωeSQG and ωOFES at 50 m (a) and 100 m (b) in the South China Sea from March 2012 to February 2013

3.3 典型区域垂向流速诊断

根据南海中尺度动力过程[31]和时间相关系数rt的分布特征，选择R1–R5 5 个典型区域对比分析，5 个区域的范围如图4 所示。其中，R1 区位于台湾西南部（19°～21.5°N，115°～119.5°E），该区域的动力过程主要受到黑潮入侵南海的影响。R2 区位于越南以东（9°～15°N，110.5°～113°E），其中尺度过程主要与越南季风急流有关。R3 区位于菲律宾西部（12°～14°N，115°～119°E），该区域中尺度过程较弱。R4 区位于南海南部（7°～ 9°N，112°～116°E），R5 区位于海南岛东北部（19.5°～21°N，111.5°～114.5°E），这两个区域的动力过程受岛屿地形影响较大。R1 和R2 区rt普遍达到0.5 以上，定义为高值区。R3 区rt整体较小，定义为低值区。R4 和R5 区属于陆架海域，其垂向流速变化复杂，定义为陆架区。

图5 给出了R1–R5 区ωeSQG和ωOFES空间相关系数rs的垂向时间序列及其年平均和季节平均结果。如图5a 所示，R1 区rs除8 月100 m 层以深存在明显负值外，其余时间段均为正值，其中5 月和冬季量值较大。R1 区的年平均rs为0.20～0.44，随着深度的增加而先增大后减小（图5b）。冬季和夏季rs随深度的变化与年平均结果相似，但夏季rs整体量值较小为0.05～0.45，冬季较大达到0.21～0.54（图5c）。值得注意的是，上层80 m 夏季rs较冬季大，这可能是因为夏季整体混合层深度较浅。R2 区rs在2 月、5 月和10 月量值较大（图5d）。R2 区rs负值分布相比于R1区更为分散，在许多月份上层500 m 均存在负值。R2区的年平均rs随深度的变化与R1 区相似，但R2 区整体量值较小，为0.13～0.39（图5e）。R2 区的冬季和夏季rs随深度的增加均先增大后减小，冬季R2 区rs在上层500 m 均大于夏季，最大值所在深度比R1 区较浅（图5f）。整体来看，冬季高值区rs及其最大值所在深度均较夏季大，表明eSQG 更适用于诊断冬季高值区的垂向流速。年平均和季节平均rs随深度增加都呈现先增大后减小的趋势，这一结果与前人在大洋区域研究结果相似。某些时间高值区的rs为负值，这是eSQG 应用于大洋区域所没有的现象。

图5 R1–R5 区ωeSQG 和ωOFES 空间相关系数rs 的垂向时间序列及其年平均和季节平均结果Fig.5 Time series,yearly average and seasonal average of correlation rs between ωeSQG and ωOFES in regions from R1 to R5

由图5g 可知，R3 区rs随时间变化呈现正负交替的特征，无明显的季节变化。rs在混合层以浅比混合层以深大，这与前人在大洋区域的研究结果相反。年平均rs随深度的增大而减小，最大值为0.17，相比高值区的结果小（图5h）。冬季和夏季rs也随深度的增加而减小，200 m 层以浅冬季rs大于夏季，而后相反（图5i）。对比高、低值区rs结果可知，低值区rs整体量值比高值区小，混合层以浅rs垂向变化呈现相反的趋势。

由于陆架区大部分区域水深较浅，200 m 以深的ωeSQG和ωOFES样本数量较少，比较二者差异的误差较大，因此陆架区只考虑200 m 以浅的结果。R4 区rs类似于R3 区呈现正负交替态势，混合层上下差异不明显（图5j）。R4 区的年平均rs随深度增加先增大至约60 m 深度达到最大值0.19，而后随深度快速减小，到200 m 深度接近于0（图5k）。冬季rs相比夏季大，60 m 处高值达到0.26，是夏季的两倍左右。由图5m可知，200 m 以浅R5 区rs基本为正值。R5 区的年平均rs随深度变化以振荡的形式整体减小，其量值为0.08～0.25（图5n）。冬季和夏季在100 m 上下相对大小相反，不同于其他区域，R5 区上100 m 层rs夏季更大（图5o）。

统计R1–R5 区rs的概率分布并对其进行功率谱密度分析，结果如图6 所示。R1 区rs最大概率区间为0.3～0.4，占比达到26%（图6a）。R2 区rs的概率分布与R1 区相似，最大概率区间略小（0.2～0.3），占比为19%（图6c）。R1 和R2 区rs均以正值为主且35%以上大于0.4，表明eSQG 能较好诊断高值区的垂向流速。功率谱图显示，R1 区各深度rs存在能量密度较强的约30 d 和50 d 变化周期，而高频信号（周期为20 d 以内）的能量密度普遍较弱（图6b）。由图6d 可知，R2 区rs在30 d 以上周期能量密度普遍较强且随深度的变化不明显。R2 区rs的20 d 以下的高频信号较R1 区强，表明R2 区可能存在更多高频过程。两个区域均存在30～50 d 的周期，表明两个区域rs的变化可能受同一种动力过程影响。

R3 区rs最大概率区间为0.1～0.2，占比为19%。虽然正相关系数占比为59%，但其0.3 以上高相关系数的负值概率更大（图6e）。R3 区rs的正负值占比差异不大，体现了rs随时间变化正负交替的特征。此外，R3 区rs主要为–0.2～0.2（占比59%），表明R3 区rs主要为低值。R3 区功率谱图显示，rs时间变化存在约45 d 和75 d 的明显变化周期（图6f）。30 d 以下的高频信号能量密度相对较小，这种对比特征与高值区类似，但R3 区rs高频能量高于R1 区和R2 区。并且500 m 深度能量密度普遍大于表层能量密度，这可能是因为导致rs变化的动力过程主要发生在深层。

R4 区最大概率区间为0～ 0.1，占比为14%（图6g），R5 区最大概率区间为0.2～0.3，占比为23%（图6i）。R4 区rs正、负值占比分别为64%和36%，rs正、负值占比差异不大，体现了正负交替的时间变化特征。R5 区rs正、负值占比分别为84%和16%，占比差较R4 区大，主要是因为R5 区上层200 m 的rs基本为正值。由图6h 可知，R4 区rs在30～50 d 周期的能量密度最强，能量密度随深度的变化不明显。高频信号的能量密度在底层较强，主要呈现约20 d 的周期。R5区rs主要表现为20～30 d 的周期，能量密度在底层较大（图6j）。陆架区的高频信号能量普遍较强，这与高、低值区存在较大差异，可能是受底边界的影响。

图6 R1–R5 区ωeSQG 和ωOFES 空间相关系数rs 的概率分布及其功率谱Fig.6 Probability distribution and power spectra of correlation rs between ωeSQG and ωOFES in regions R1 to R5

4 讨论

4.1 数据时空分辨率对诊断结果的影响

4.1.1 时间分辨率影响

为了探究不同时间分辨率对eSQG 在南海垂向流速诊断结果的影响，将原3 d 时间分辨率SSH 数据平均为9 d 时间分辨率，进而计算ωeSQG，并与9 d 平均的ωOFES进行对比分析。图7 示出9 d 时间分辨率南海ωeSQG和ωOFES的空间相关系数的垂向时间序列。可见，9 d 分辨率和的整体趋势和量值都与3 d 分辨率结果相似。对比年平均和季节平均结果可知，两种时间分辨率的结果差异很小。年平均和冬季在150 m 深度以深相对3 d 分辨率结果稍有增大，夏季表现为无明显差异。年平均相对3d分辨率结果在120 m 以深增大，夏季基本不变，冬季表现为80 m以深增大。不同时间分辨率和在量值上的差异可能是时间分辨率降低导致样本数减少引起的。整体来看，和的变化不大，可以认为改变时间分辨率不会影响eSQG 在南海的适用性。

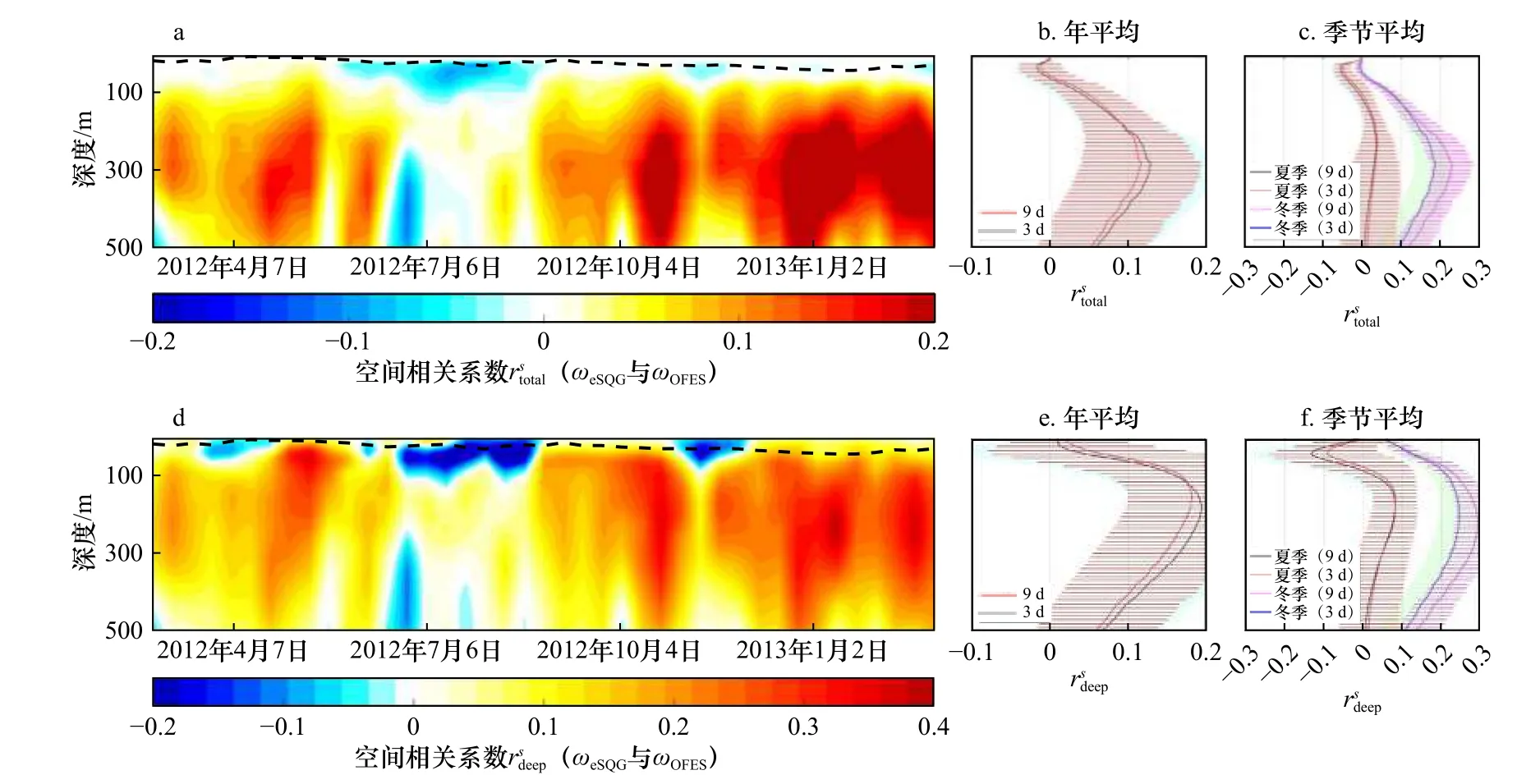
图7 9 d 时间分辨率南海ωeSQG 和ωOFES 的空间相关系数和 的垂向时间序列（a,d）及其年平均（b,e）和季节平均（c,f）Fig.7 Time series (a,d),yearly average (b,e) and seasonal average (c,f) of correlation and between ωeSQG and ωOFES in the South China Sea derived from data with temporal resolution of 9 days

4.1.2 空间分辨率影响

为了探究不同空间分辨率对eSQG 的影响，将原0.1°×0.1°空间分辨率的SSH 数据线性插值为0.25°×0.25°分辨率，进而计算ωeSQG，并与0.25°分辨率的ωOFES进行对比分析。图8 示出0.25°×0.25°空间分辨率南海各深度ωeSQG和ωOFES的空间相关系数的垂向时间序列。0.25°分辨率的和表现出与0.1°分辨率相似的时空变化趋势，但整体量值明显增大。年平均和季节平均结果显示，和在3 种情况下相对0.1°分辨率结果均增大。其中，的增幅基本达到0.1，的增幅基本达到0.08，二者增幅的差异可能是因为计算的范围更大，受空间分辨率的影响更明显。另一方面，和的增幅在时间变化上大致表现为冬季最大，年平均次之，夏季最小，这可能是因为0.25°分辨率过滤了某些非地转过程。整体来看，可以认为0.25°分辨率有利于eSQG 诊断南海垂向流速。前人研究显示，当相对涡度较大、非地转增强时，eSQG 诊断效果会有所下降[32]。因此，0.25°分辨率数据时eSQG 的适用性强于0.1°分辨率。

图8 0.25o 空间分辨率南海ωeSQG 和ωOFES 的空间相关系数 和的垂向时间序列（a,d）及其年平均（b,e）和季节平均（c,f）Fig.8 Time series (a,d),yearly average (b,e) and seasonal average (c,f) of correlation and between ωeSQG and ωOFES in the South China Sea derived from data with horizontal resolution of 0.25o

4.2 诊断效果随时间变化的可能原因

前文分析显示ωeSQG的时空特征表现为夏强冬弱、北强南弱，rs在台湾西南部和越南以东较高。为了探究上述研究结果的成因，图9给出了3种情况南海100m深度的相对涡度ζ/f（f=5.6×10−6Hz 是14°N 的科氏参数）的水平分布。可见南海整体相对涡度在陆架边缘较大，海盆内部较小。相对涡度基本在0.1 的量级，表明南海的运动尺度以中尺度为主，符合eSQG 诊断垂向流速的适用尺度。南海相对涡度呈现夏强冬弱、北强南弱的时空特征，说明ωeSQG的时空特征可能受到相对涡度的影响。另一方面，台湾西南部和越南以东的相对涡度普遍较其余区域大，这是eSQG 在这两个区域的诊断效果较好的原因。

图9 年平均、夏季和冬季南海100 m 深度相对涡度的水平分布Fig.9 Horizontal distribution of relative vorticity at 100 m in the South China Sea in the whole year,summer and winter

除了季节变化，同一区域eSQG 诊断流速与OFES模拟“真值”的差异，在时间上存在很大变化。以诊断结果相对较好的R1 区为例，ωeSQG和ωOFES的相关系数也存在明显周期变化。为探究eSQG 诊断效果随时间变化的原因，对比R1 区海面高度SSH、诊断流速ωeSQG以及ωOFES谱分析结果。如图10a 所示，研究区SSH 存在约18 d、26 d、46 d 和73 d 的周期变化，这与研究区中尺度涡旋、地形罗斯贝波和固有模态等因素有关[24,35–36]。对应SSH 变化，R1 区ωeSQG的能量密度随深度的增大而增大，也存在约18 d、24 d、30～40 d、45～55 d 和90～100 d 的周期，表明ωeSQG与中尺度过程变化密切相关（图10b）。对比rs的功率谱图（图6b），其变化主 周期20～30 d 和45～60 d 可与SSH 和ωeSQG变化周期相对应。ωOFES谱分析结果显示，其存在对应SSH 和ωeSQG约18 d 和46 d 的周 期。ωeSQG与ωOFES相关性在时间上的变化可能受中尺度过程影响较大。

图10 R1 区海面高度（SSH）（a）、ωeSQG（b）和ωOFES（c）谱分析结果Fig.10 Power spectra of sea surface height (SSH) (a),ωeSQG (b),and ωOFES (c) in the Region R1

进一步根据100～500 m 深度平均的rs将研究时间段分为3 种情况：rs<0，定义为负相关期；0～0.5 定义为低相关期；0.5～1 定义为高相关期。3 种情况下，R1 区合成平均的SSH 和海面密度（Surface Sea Density，SSD）的水平分布如图11 所示。可见，负相关期，SSH 呈现空间对称分布，东北角存在明显的气旋涡（图11a）。此时，SSD 在东北角也存在明显的高值区，南部SSD 普遍较大（图11d）。SSH 和SSD 的相关系数为–0.27（p<0.01），二者呈现反相关关系。低相关期，SSH 整体差异较小（图11b），中南部SSH 较小，西北部较大。同时期SSD 在北部较大，东南部较小。SSD 与SSH 的相关系数较小，为0.15（p<0.01）。高相关期，SSH 沿纬度方向存在弯曲的特征，北部较大，南部较小。SSD 北部整体较大，东南部较小，其分布特征与同时期SSH 相似。SSH 和SSD 的相关系数高达0.56（p<0.01）。可见，eSQG诊断南海垂向流速与SSH和SSD的相关性有关。结合前人研究结果[18–19]：当SSH 与SSD 存在相同的相位时，eSQG 诊断结果更接近真值。eSQG 诊断结果在时间上的差异可能是由SSH 与SSD 相位差异造成的。

图11 负相关期、低相关期和高相关期R1 区海面高度（SSH）和海面密度（SSD）的水平分布Fig.11 Horizontal distribution of sea surface height (SSH) and surface sea density (SSD) in the Region R1 during period of negative correlation,low correlation and high correlation

4.3 与其他模式结果的对比

最近，Zhu 等[37]利用分辨率为（1/12）°的HYCOM（Hybrid Coordinate Ocean Model）水平流速数据，根据质量守恒估算了2012 年8 月至2013 年9 月时间平均的南海50 m 和250 m 深度的垂向流速。研究结果显示，南海垂向流速整体北强南弱。在季节变化上，Zhu 等[37]结果显示是夏强冬弱，跨岸线方向呈正负交替的带状分布；冬季和夏季垂向流速在时间变化上存在季节性的正负颠倒，这一现象在近岸海域最为明显。与之相比，本文eSQG 诊断南海垂向流速ωeSQG同样表现为北强南弱，夏强冬弱，冬季台湾西南部少数海域存在跨岸线方向的正负交替带状结构，季节性颠倒的特征不明显。ωOFES则表现为北强南弱，冬强夏弱的时空特征，无明显的带状结构和季节性颠倒。Zhu等[37]在计算垂向流速之前对水平流速数据进行了九点平滑处理，因此其研究结果主要显示南海垂向流速的中尺度时空特征。OFES 模式的数据分辨率为0.1°，其模拟结果可能包含部分次中尺度过程，因此ωOFES呈现冬强夏弱的时空特征。另一方面，eSQG 能较好诊断垂向流速的中尺度时空特征，因而ωeSQG呈现与Zhu 等[37]估算垂向流速相似的时空特征。

5 结论

本文利用OFES 模式0.1°高分辨率的温盐、流速和海面高度数据，运用eSQG 方法诊断估算了南海垂向流速的时空分布，并与OFES 模式垂向流速对比分析。主要结论如下：

（1）在南海海域，ωeSQG空间分布均以14°N 为界，呈现北强南弱的特征，ωeSQG强度从南海东北部O（10−5m/s）减弱到西南部O（10−6m/s）。在时间变化上，ωeSQG呈现夏强冬弱的时间特征。其时间特征与ωOFES相反。ωeSQG与ωOFES水平空间相关系数rs在冬季最高、夏季最小。二者吻合程度在深水区明显高于全海域，说明eSQG 诊断效果在远离地形的深水区更有效。eSQG 方法在混合层以下诊断效果较好，在次表层150 m（320 m）上下达到最大，之后随深度的增加而减小。

（2）eSQG 方法在台湾西南部和越南以东等中尺度涡活跃区的适用性较好，ωeSQG与ωOFES时间变化相关系数rt普遍高于0.5，35%以上空间变化系数高于0.4；菲律宾西部深水区以及南海南部和海南岛东北部的陆架区rt小于0.2，60%以上空间相关系数rs小于0.2。各区域rs存在明显时间变化，变化周期基本在18～55 d 之间，反映了中尺度过程对eSQG 的影响。对比SSH 与SSD 空间分布显示，当SSH 与SSD 的相位相同时，eSQG 诊断结果较好。

（3）海面高度数据的时间分辨率对eSQG 诊断结果的影响不明显；空间分辨率降低为0.25°时，ωeSQG与ωOFES空间系数增大，说明eSQG 诊断在中尺度上更适用。