NLOS 状态信息辅助协方差矩阵修正的无线网络定位方法*

闻建刚，岳洋洋，华惊宇*，倪郑威，徐志江，余绪涛

(1.浙江工商大学信息与电子工程学院，浙江 杭州 310018；2.浙江机电职业技术学院自动化学院，浙江 杭州 310059；3.东南大学移动通信国家重点实验室，江苏 南京 210096)

移动通信设备的不可或缺性促进了无线通信技术的发展，对于未来的6G 乃至7G 技术来说，实现空间物体之间的紧密互联是一个极大的挑战[1]。万物互联将使得物联网与通信网紧密相连，传感设备通过无线网络获取各个节点的感知信息，并作进一步处理，在这个过程中，位置信息的获取必须足够准确。因此，如何根据已知信息来判断可移动节点的位置在物联网发展中具有重要的研究价值，无线网络定位技术的发展便是源于物联网的定位需求[2]。

近年来，相关定位系统的研究在逐步完善中，不同环境下的定位技术精度也有了大幅度的提升[3]。在无遮挡视距(Line-Of-Sight，LOS)的室外环境下，现有定位技术的精度已经能满足绝大多数的应用场景，例如车辆导航、个人定位、围栏管理、超速管理、紧急求助等。但是，在包含众多建筑物的复杂室外环境或者非视距(Non-Line-Of-Sight，NLOS)环境中，定位精度会下降[4]。就具体的无线定位而言，其实现可以采用信号到达时间(Time Of Arrival，TOA)[5]、信号到达角度(Angle Of Arrival，AOA)[6]、信号到达时间差(Time Difference Of Arrival，TDOA)[7]、接收信号强度(Received Signal Strength Indication，RSSI)[8]以及混合参数等方法，而测距误差和NLOS 误差的存在会导致这些传统定位方法的准确度下降[9]。在实际环境中，测距误差和NLOS误差的存在都是随机的，前者一般符合高斯随机分布，后者由于定位环境的多变性很难找到一个准确的描述模型，故而被认为是无线传感器网络定位的主要误差来源[10-11]。因此，在NLOS 误差环境下，如何解决其对定位精度的影响是一个严峻的挑战。

针对上述问题，研究人员从不同角度提出了减小NLOS 误差影响的方法，例如:对NLOS 误差进行模型训练[12]、对NLOS 节点进行识别[13]等。在文献[10，12]中，研究人员将信道的统计特性用做NLOS的识别条件，而这种做法需要确定特征参数的联合分布，计算复杂，且LOS 节点的识别准确率只有90%。文献[14]提出了一种增强的基于到达时间的定位算法，尽管不需要NLOS 误差的分布信息，但是需要NLOS 测量情况已经确定，不适用于多变的实际情况。文献[15]通过遍历拓扑中的锚节点作为参考点来估计位置，再将这些估计位置的线性组合作为最终结果，但是其研究过程中固定了NLOS节点的分布情况，且算法复杂度较高。文献[16]提出了一种利用固定锚节点几何特征的改进加权定位算法，它针对三个锚节点固定的环境，将所得到的数据进行遍历求解。文献[17]提出一种分两个阶段实现的闭式估计算法，首先利用距离的偏差模型导出距离估计，再使用三边测量法来找到移动节点的具体位置；该算法的缺点是要求至少存在三个固定锚节点，还需要已知所在环境的几何特征，因此其环境适用性较差。文献[18]提出一种LOS 节点检测的方法，称为双步加权最小二乘(Two Step-Weighted Least Square，TS-WLS)算法，该算法改善了前述算法中对于锚节点个数的要求，同时提高了NLOS 识别准确率，但是仅使用LOS 节点进行定位，导致其仅能在NLOS 节点分布固定的条件下获取较好的定位性能。

针对TS-WLS 定位算法存在的问题，本文对其进行改进，提出了一种基于协方差修正的TS-WLS定位算法，其实现的主要思想如下:运用已有的NLOS 节点识别技术，对锚节点拓扑进行识别，将得到的LOS 和NLOS 节点信息用于TS-WLS 算法中协方差矩阵的调整更新，使得含有NLOS 测距的锚节点对定位结果的贡献降低，但又充分包含了所有测距信息的作用，从而改善无线定位性能。

1 TS-WLS 定位算法

在定位实现的过程中，拓扑由锚节点(anchor node，AN)和移动节点(mobile node，MN)构成，系统根据传感器测得的距离及角度信息对定位过程中各个变量进行设置并用于定位计算。根据得到的拓扑信息，将第k个AN 和MN 的实际距离rk表示为:

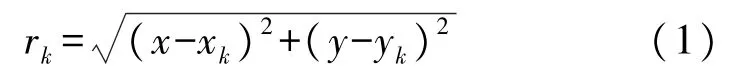
式中，(x，y)表示MN 的位置坐标，(xk，yk)表示第k个AN 的位置坐标，受到测距噪声以及NLOS 误差影响的测量距离表示为:

式中，ek表示测距噪声，nk表示NLOS 误差。

同理，真实到达角度的正切值可以根据节点位置信息获得，即:

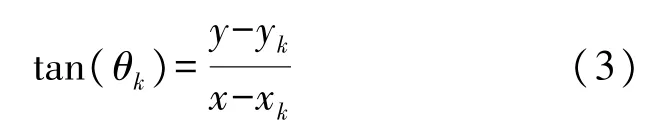
θk表示第k个真实角度数值，测量角度为:

式中，αk和βk分别表示角度测量噪声以及NLOS 误差影响。

利用上述边长和角度信息，定位问题可建模为如下表示[18]:

式中，X＝[x，y，R]T，R＝x2＋y2，N表示拓扑中的锚节点总数，此外

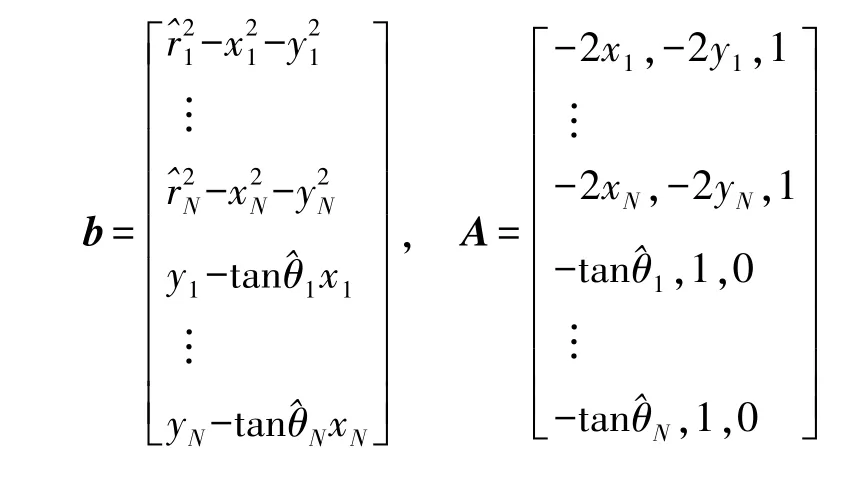
利用最小二乘法(Least Square，LS)对问题(5)进行求解，可得

由于定位参数测量值包含测距噪声，最小二乘法求出的位置估计并不准确，需要对结果做进一步优化。

由测量噪声导致的位置估计误差矢量可以近似为:

将上述表达用矩阵向量形式改写为:

利用以上所得协方差矩阵对LS 进行改进，所得WLS 求解结果如下[18]:

由于运算过程中实际位置数值未知，仅能利用测量距离来近似代替移动节点与锚节点之间的实际距离，因此对于涉及到距离的变量，需要WLS 算法进行多次迭代，再将每次得到的位置估计值代入其中，直到得到一个较为鲁棒的数值结果，该结果相比单纯使用LS 算法具有更高的定位精度[19]。

当处于室内或者多遮蔽物的环境中，测距结果中除了测量噪声还有随机性很强的NLOS 误差，会严重降低测距和测角的精度，因此需要考虑针对性的处理方法，来减小NLOS 误差对定位精度的影响。

2 基于协方差矩阵修正的改进定位算法

当定位参数测量中含有NLOS 误差时，增加锚节点的数量或者增加TS-WLS 算法中迭代次数不能对定位误差产生足够的削弱，而文献[18]中的锚节点检测方法可以识别LOS 节点，在其设定的识别条件下，对LOS 节点的识别准确率可以达到93%以上。此外，NLOS 环境中TS-WLS 算法的定位误差主要来源于协方差矩阵元素的失配，因此可以考虑结合NLOS 检测信息对协方差矩阵进行修正，从而改善TS-WLS 算法在NLOS 环境的定位性能。

在式(8)中，协方差矩阵的数值主要由对角矩阵Q确定。考虑存在NLOS 误差的环境，则Q矩阵中的元素值应需修改为含有NLOS 误差的测量数据方差。实际上，我们无法获得该数值，也无法使用LOS 环境下的测量噪声方差。因此，本文提出了一种修正方法，结合NLOS 检测信息和测量噪声方差对Q矩阵元素进行修正，使其更贴近真实的方差值。

图1 显示了由锚节点A＆B、移动节点C 构成的三角拓扑，利用传感器测得三者间的距离为{a，b，c}，角度信息为{θ1，θ2，θ3}。由于存在遮挡物D，测得的距离b与实际距离b′存在偏差，文献[18]将该偏差称为边长残差。基于该残差，本文提出了协方差矩阵修正方法。

图1 几何节点拓扑示意图

计算边长残差时由于实际距离未知，使用计算距离代替。根据三角拓扑中的测量距离、角度信息可以计算出MN 与锚节点之间的计算距离。在包含N个锚节点的测距拓扑中，计算第k个锚节点ANk与MN 之间的计算距离时，ANk可以同MN 及其他N-1 个锚节点各组成N-1 个三角拓扑，由于每个三角拓扑中对应的角度值以及测距误差不同，因此锚节点ANk与移动节点MN 之间的计算距离在不同拓扑中也会有差距。

实际计算时，将MN、锚节点ANk与剩余N-1个锚节点中一个AN 构成三角拓扑中的计算距离记录为Rki(i＝1，2，3…N；i≠k)，MN 与锚节点ANk共N-1 组计算距离，同时根据计算距离Rki与测量距离dk求得MN 与锚节点ANk的N-1 组边长残差数值ΔANki＝｜dk-Rki｜，(i＝1，2，3…N；i≠k)[18]。

边长残差可以用作NLOS 节点的判断依据，表示NLOS 误差的严重程度，但是不能直接将其用于NLOS 修正中。因此，本文使用MN 与ANk之间边长残差的均值来代表的其NLOS 误差影响系数εk，具体表示为:

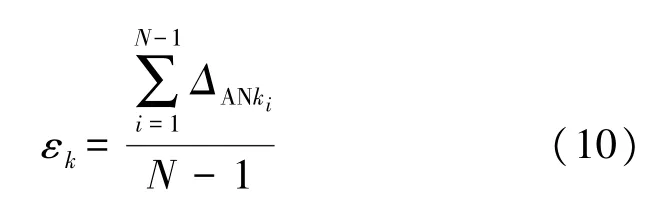
为了将εk与NLOS 误差对应，需要先将边长残差按照NLOS 误差分布的最大值Δmax、最小值Δmin进行归一化设置，之后将归一化后的边长残差按照从小到大进行排序，得到ΔANkj(j＝1，2，3…(N-1))。

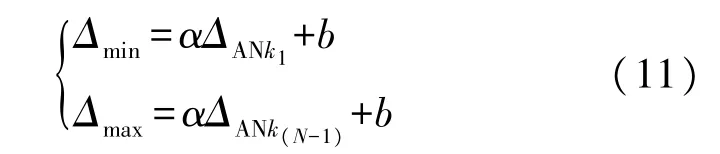
进而，相关的线性内插关系可表示为:

将NLOS 误差影响系数εk代入上式即可得到代表NLOS 误差大小的参数δkr

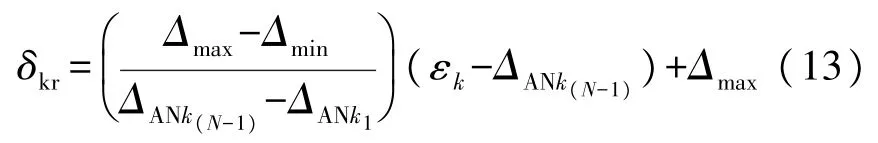
在Q矩阵中用于角度部分的修正参数可以使用线性转换来获得:

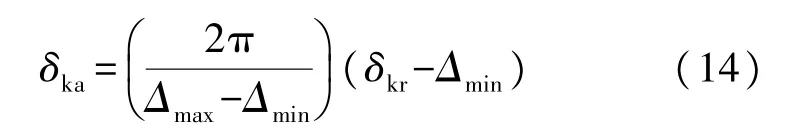
将以上δkr、δka代入式(8)中的矩阵Q，所得修正结果表示为:

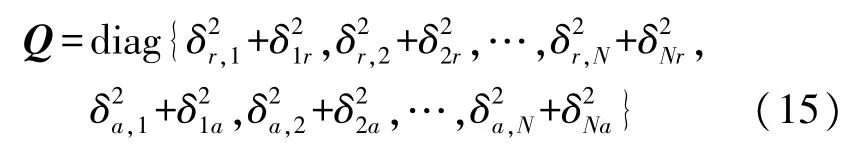
式中，经过锚节点检测之后被认为是LOS 节点的不需要修正。

与文献[18]中仅采用LOS 节点进行TS-WLS定位不同，本文使用全部锚节点进行移动节点的位置估计。具体的执行过程如下:

①进行LOS 节点检测，筛选出LOS 节点，并记录下移动节点相对于各节点的边长残差ΔANki，其中i＝1，2，3，…，N，且i≠k；

②进行Q矩阵修正参数的计算:

1)若节点k是LOS 节点，设置Q矩阵修正参数δkr＝0；

2)若节点k是NLOS 节点，先计算εk，再将其代入式(13)并进一步计算式(14)，得到修正参数δkr和δka；

3)将修正参数代入式(15)，得到修正后的Q矩阵；

③用修正后的Q矩阵代入TS-WLS 算法进行位置求解。

3 计算机仿真与分析

本文节点拓扑选用经典的5 节点(锚节点)模式，节点之间的距离为100 m，具体坐标分布如图2所示。对图中5 个AN 进行两两分组之后，可分别与MN 组成类似图1 的三角拓扑。

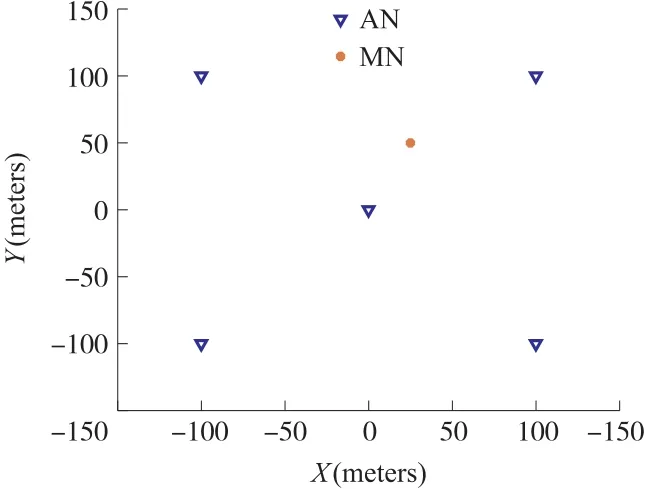
图2 AN-MN 网络拓扑

在文献[18]的仿真中，固定了移动节点的位置，并在拓扑内固定了NLOS 节点，即每次仿真时NLOS 的节点序号都是相同的。在本文的仿真中，将移动节点的位置和NLOS 节点的选取都随机化，从而模拟真实环境。相关仿真参数设置为:测量距离标准差(Standard Deviation of Range，SDR)取值为1 m，测量角度标准差(Standard Deviation of Angle，SDA)取值为1 弧度，NLOS 距离误差均匀分布在10 m到50 m 之间，NLOS 角度误差在[-π，π]之间均匀分布。在计算机仿真的定位计算中，在每种条件设定下所进行的仿真次数均为1 000 次。

仿真中，将本文所提算法与传统算法进行比较分析，对比的算法如表1 所示，重点和文献[18]算法对比。文献[18]算法的结果针对固定NLOS 节点的场景，定位计算仅使用LOS 测量结果，TS-WLS 计算中的矩阵大小和LOS-BS 数量成正比；本文方法采用了更多的锚节点参与定位，在不减小定位精度的前提下拓展了方法的适用场景，但由于矩阵大小与拓扑中AN 数量成正比，在求解时参与的AN 数量会有所上升，增加了一定的复杂度。在经典定位中，拓扑采用的AN 数量不大，以目前的计算能力而言，增加的复杂度是可以承受的。另一方面，本文方法属于线性处理方法，比最优化的CLS 方法要简单；而RWGH 在分组估计后直接进行加权合并计算，无需迭代，实现复杂度最小，而代价是定位精度差。

表1 算法说明

仿真中，使用均方误差(Root Mean Square Error，RMSE)来对比分析SDA 和SDR 取值变化对各类算法定位精度的影响，结果如下。

①SDA 的影响

如图3 所示，随着SDA 的变大，约束最小二乘法(CLS)以及残差加权算法(RWGH)由于没有采用角度信息，故RMSE 的趋势始终保持平稳，两者的误差相对最大。本文算法与文献[18]算法误差都随着SDA 的增大而增大，本文算法略高，但是文献[18]方法的仿真固定了MN 位置和NLOS 锚节点的序号。随着NLOS 影响的加剧(NLOS 节点数量的增加)，其性能将比本文方法发生相对更明显的恶化。而且本文方法对于NLOS 节点设置没有限制，拓展了算法适用范围。

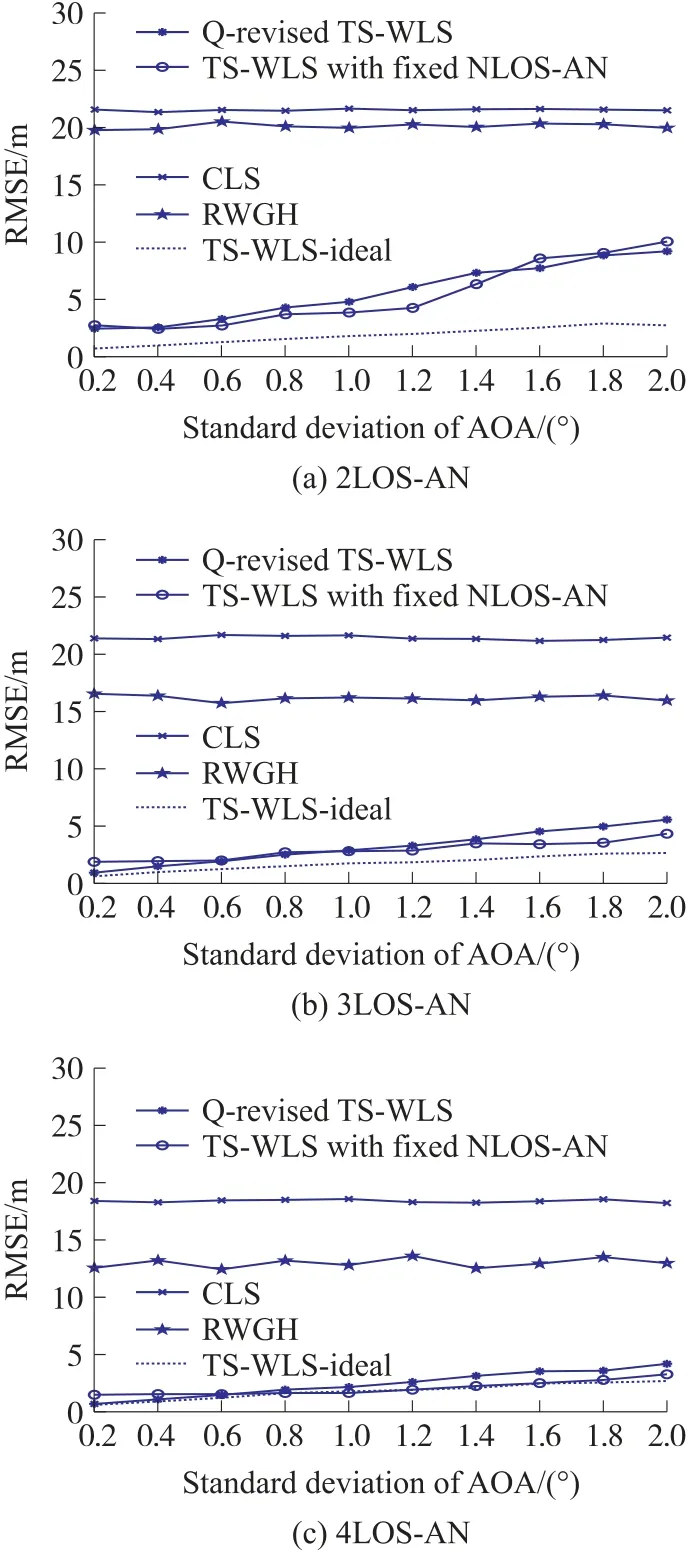
图3 SDA 取值对定位算法的影响

图3 中取SDA＝1，几种算法的RMSE 结果对比如表2 所示。从表中可以看出，在文献[18]限制仿真条件情况下，本文提出算法与文献[18]算法相比差距不是很大，随着LOS 节点数的增加，两者间的定位精度差距减小。与其他传统算法相比，由于NLOS 最大值偏大，CLS 和RWGH 对NLOS 误差的对抗能力不足，同时也没有采用角度信息，导致这两种方法定位精度相对较差，相差约一个数量级。

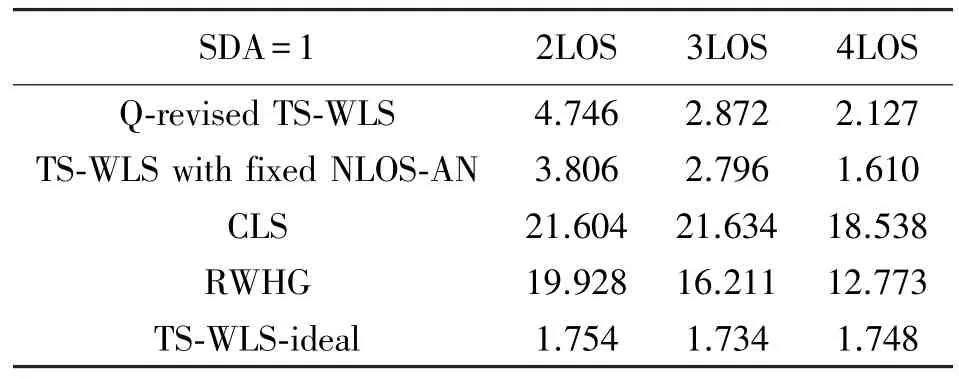
表2 SDA＝1 时几种算法RMSE 结果 单位:m

②SDR 的影响

图4 展现了SDR 对算法精度的影响，由图中曲线的变化可以看出，约束最小二乘法(CLS)的定位精度与SDR 的变化没有关系。随着LOS 节点数量的增加，残差加权法(RWGH)的均方误差值逐渐变小，然而与理想TS-WLS 算法相比，还存在着不小的误差。由于本文方法中的MN 和NLOS 节点均随机化，使得定位性能最终与文献[18]的方法相比有少量差距。此外，随着LOS 节点数量的增多，本文方法的定位精度可以与理想TS-WLS 算法的定位精度接近一致，证明了本文算法优异的定位性能。

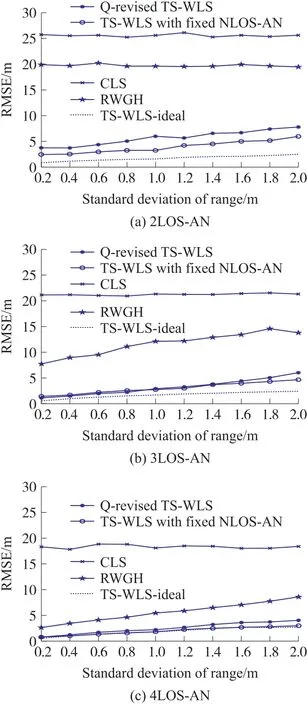
图4 SDR 取值对定位算法的影响

图4 中取SDR＝0.4，几种算法的RMSE 结果对比如表3 所示，同表2 中结果类似，本文算法相对于约束最小二乘法(CLS) 以及残差加权算法(RWGH)，均方误差值有很大的提升。此外，由于文献[18]算法仿真条件有所限制，本文算法尽管相较于文献[18]算法在定位结果上有少量差距，但是突破了前者NLOS 节点固定的场景设定。

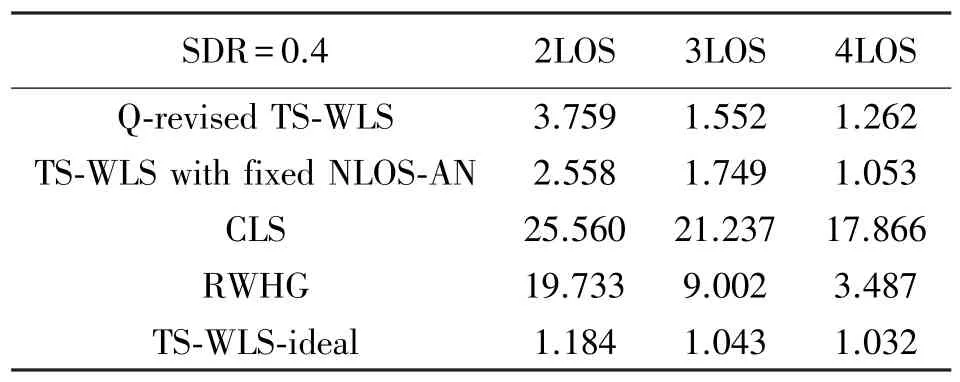
表3 SDR＝0.4 时几种算法RMSE 结果 单位:m

此外，为了观测定位误差的分布情况，图5 展示了算法的累计分布函数(Cumulative Distribution Function，CDF)曲线图。图中对CDF 的测试基于拓扑中有3 个LOS 节点的情况，同时SDR ＝1、SDA ＝1。曲线结果表明:在移动节点与NLOS 节点位置分布完全随机的情况下，当定位误差为5m 时，本文算法的CDF 为0.9，结果仅为定位半径的5%，逼近文献[18]固定移动节点以及NLOS 节点位置时所得到的结果，表明了本文所提出协方差修正方法的有效性。该修正方法不仅改善了TS-WLS 定位方法的性能，且相对于文献[18]方法放宽了定位算法的约束以及拓展了定位算法的应用范围。

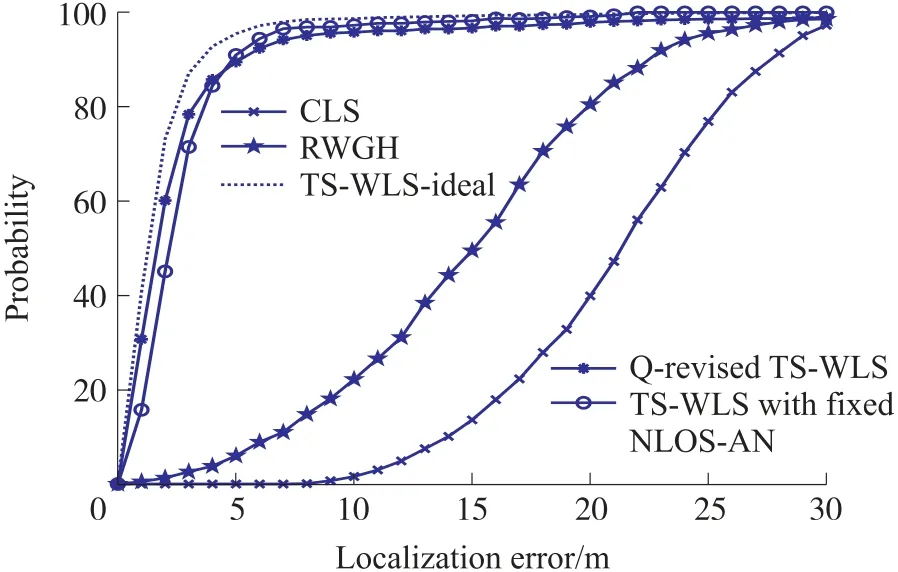
图5 不同算法的CDF 对比图

4 结论

为解决NLOS 误差对无线定位精度的影响，本文利用LOS 技术检测得到的误差信息对TS-WLS 定位算法中的协方差矩阵进行修正，并通过线性内插方法对权重值进行设置，一方面充分利用所有测距信息，另一方面通过权值约束NLOS 测距信息对定位结果的影响，从而减小定位误差。仿真结果表明，本文提出的方法拓展了复杂NLOS 场景下的适用性，相比传统算法有优势，能够改善定位性能。