水平定向扩孔器破岩切削力矩仿真研究

葛昭文 燕 翌 张 戈 李 云

（1.西安交通大学化学工程与技术学院；2.西北工业大学力学与土木建筑学院；3.中石化中原油建工程有限公司）

非开挖技术作为在地表不挖槽和地层结构破坏极小的情况下对各种管线进行铺设、修复和更换的施工技术，广泛应用于石油、天然气工程中。 而水平定向扩孔器作为非开挖技术中的关键设备，由于进尺速度缓慢、扩孔切削力矩难以控制，在脆性岩土地质中进行扩孔过程时，容易产生大块岩屑孔内堆积、破碎地质钻屑不易带出等问题［1］。 因此，有必要针对不同岩质，研究分析扩孔器切削力矩，减少对孔壁的扰动，同时提高钻机扩孔速度和切削速度，提高扩孔的施工效率和成孔质量。

目前扩孔器破岩过程中的切削力矩确定方式多为传统理论计算求解法［2］，利用该方法确定切削力矩较为简单，但因求解时未考虑岩体破碎的脆性特征，认为破岩过程中切削齿和岩体处于完全接触的状态［3］，力矩计算结果往往偏大，导致扩孔器功率过大，切削振动现象加剧，从而发生卡钻等事故。 GOKTAN R M和YILMAZ N G通过实验的方式研究了扩孔器切削岩土的特征，发现岩土的切削效率会随着岩土脆性的增加而提高［4］；LI X F等用离散元方法研究了岩石脆性对岩石破碎和切削性能的影响。 研究认为在切割脆性较大的岩石时，切削力波动较大且切削效率比低脆性岩土要高［5］。 上述研究表明岩土切削力和岩土脆性密切相关。

笔者在考虑岩体脆性破碎特征的情况下，对扩孔器工作过程进行力学分析，建立扩孔器破岩的有限元模型，利用Abaqus软件，对扩孔器切削过程进行数值仿真，以期获得脆性岩土中扩孔器所需的最低切削力矩， 同时研究岩质力学参数、扩孔器关键参数对切削力矩的影响，为实际工作扩孔器切削力矩的选取、结构优化、扩孔速度的提高提供理论依据。

1 扩孔器-岩土相互作用分析

扩孔器在工作时，由钻机通过钻杆提供扩孔器绕自身轴线转动的扭矩和拉动扩孔器前进的拉力，通过扩孔器牙轮切削齿与岩体的相互作用实现对岩土的破碎，达到扩孔的目的。 图1所示为扩孔器工作示意图。

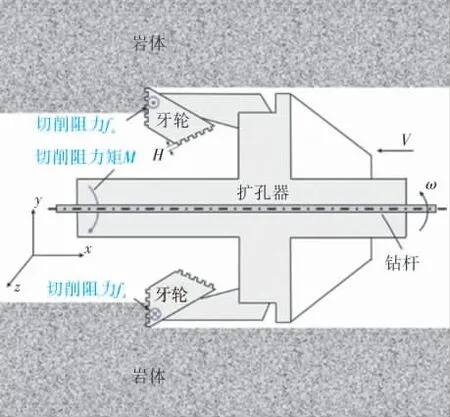
图1 扩孔器工作示意图

如图1所示， 扩孔器工作时主要受到岩土的阻力矩M，切削刃上阻力矩（切削阻力矩）M表示刀刃对土体进行切削时土体阻力形成的力矩，为：

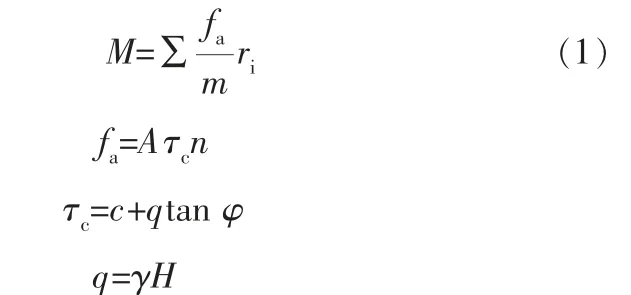
式中 A——等效接触面积， 表征切削齿和岩体的接触状态， 可由扩孔器几何结构获得；

c——岩土粘聚力；

fa——切削刃上所受的切削阻力；

H——岩土所在深度；

m——切削刃轴向组数；

n——切削刃轴向数目；

q——由岩土重力引起的围压；

ri——切削刃所在的扩孔器半径；

γ——岩土重度；

τc——土体的切削破坏强度， 同时表示切削刃切削过程中从土体所受的最大临界阻力， 可由摩尔-库伦准则计算；

φ——岩土内摩擦角。

2 扩孔器切削过程仿真

2.1 扩孔器切削仿真的基本假设

在扩孔器实际运行过程中，影响扩孔阻力矩的因素较多， 为了便于有限元仿真的研究，做出以下假设：

a. 鉴于扩孔器切削齿的强度和硬度远高于岩体，将切削齿假设为刚体，且认为在钻进过程中不发生磨损；

b. 假定岩体为连续的、均质的、各向同性的材料，且不考虑岩体中原生裂纹和初始应力场的存在；

c. 不考虑切削过程中浆液流场、温度变化对岩体的影响；

d. 当岩体单元失效后即从岩体中移除，忽略其失效对后续扩孔的影响。

2.2 切削岩土本构模型

在扩孔器破岩过程中，岩土受切削作用产生脆性破坏。 针对切削过程进行有限元模拟，需考虑受切削岩土的两类本构模型，即弹塑性本构模型和损伤断裂本构模型。 前者描述扩孔器从初始接触岩土到使之达到屈服前的应力-应变关系，后者描述岩土屈服后扩孔器继续切削工作，使岩土损伤不断累计直至断裂失效的过程，分别对应了图2所示的OC阶段和CE阶段［6，7］。

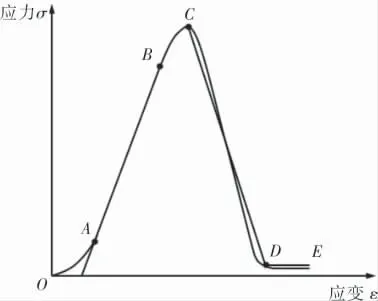
图2 准脆性破碎岩土的应力应变曲线

对于弹塑性本构，考虑岩土的特性，本研究采用了线性弹性模型和线性Drucker-Prager（D-P）塑性模型［8］，该模型改进了广义的Von Mises屈服准则［9］，可以同时反映体积应力、剪应力和中间主应力力对岩土强度的影响，且与损伤本构模型能够更好地相容。

线性弹性模型的表达式为：

式中 E——弹性模量；

δij——一个单位张量；

μ——泊松比。

线性D-P模型的屈服轨迹如图3a［8］所示，其函数为：

线性D-P模型的塑性势面如图3b［8］所示，其函数为：

图3 线性D-P模型的屈服轨迹和塑性势面

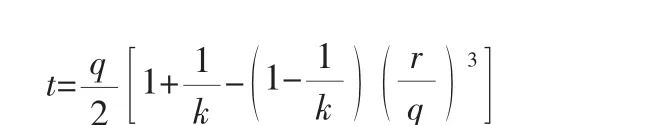
式中 d——材料的粘聚力；

k——三轴拉伸强度和压缩强度之比；

p——等效压应力；

q——等效Mises应力；

t——偏应力；

β——屈服面在p-t应力空间上的倾角，与摩擦角φ有关。

岩土损伤断裂本构模型可由应力三轴度和失效位移两个参数进行描述，较低的应力三轴度和较大的失效位移将产生韧性断裂模式，而较高的应力三轴度和较小的失效位移产生脆性断裂模式［10］。 当满足下面的条件时，会发生损伤［11］：

基于岩土的线性弹性模型、D-P塑性模型和损伤模型，不同岩质的材料参数设定见表1［12］。

表1 不同岩质的材料参数

2.3 扩孔器有限元仿真的几何模型及边界条件

扩孔器切削过程采用有限元仿真，分析软件为Abaqus 2020。 扩孔器工作时，进行切削作用的仅为牙轮上的切削齿，因此为了提高切削过程模拟的计算效率，仅建立切削齿和岩体的相互作用模型， 通过控制总接触面积S0来实现不同结构的牙轮和岩体的作用关系。

另外，实际切削过程为圆周运动，岩体在周向的力学运动模型是旋转对称的，因此，本研究建立圆周方向上的1/4旋转对称模型，这样可在不影响求解精度的情况下减少计算量。

图4为建立的切削齿和岩体接触的有限元模型。 岩体和切削齿的三维实体单位类型均采用八节点六面体线性减缩积分单元（C3D8R），单元形状使用六面体单元 （Hex）， 并采用结构化网格（Structured），且对要发生切削破坏的岩体进行网格细化以提高计算精度。 网格无关性验证结果如图5所示， 从图中可以看出随着网格尺寸的减小和网格数量的增加，切削力矩计算结果呈现先不断波动、后趋于稳定的趋势。 将网格尺寸细化至2.56 mm之后，误差仅为2.3%，另外，考虑使切削齿和岩体之间具有更好的接触关系，需要让两者初始接触面上的节点一一对应，取最终网格单元尺寸为2.5 mm。 依据潜江-韶关输气管道工程扩孔器工作参数［13］，切削过程参数设定为：摩擦系数0.4；切削齿转动幅值-1.57 rad；切削等效线速度1.884 m/s。

图4 岩体-切削齿有限元模型

图5 网格无关性验证

3 切削过程仿真结果分析

利用Abaqus/Explicit对不同岩质下各尺寸扩孔器切削岩土的过程进行动力学仿真，得到了岩体经切削破碎后的Mises应力分布结果，如图6a所示。 为了更直观体现岩体切削过程的脆性特征，将金属经切削后的Mises应力分布进行对比分析，如图6b所示。

图6 岩体和金属切削过程Mises应力分布

在切削过程中，岩体在切削齿运动的圆周方向上发生破坏，实现扩孔。 从切削后的岩体Mises应力分布图可以看出，岩体内的应力分布较为不均匀， 且整个计算岩体的应力传递较为分散，这体现了岩土脆性破坏的特点；而金属材料在切削过程中应力传递现象不明显，应力大都集中在切削路径上， 且金属被切削后形成连续的切屑，属于材料的韧性破坏。

图7为炭质灰岩和金属材料在切削过程中的切削阻力随时间的变化曲线。

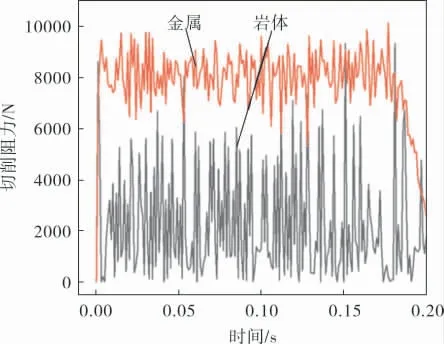
图7 不同材料切削阻力随时间变化关系

从图7可以看出，岩土材料因脆性较高，切削阻力波动程度要高于金属韧性材料，脆性岩土在动态加载下结构的损伤破坏并不均匀，这是由应力波传递［14］和材料失稳［15］双重物理机制决定的。因此切削刀具和岩土的接触面积也应处在剧烈变化之中，这导致岩土的破坏十分不稳定，切削阻力呈现剧烈的周期波动现象。 相较而言，金属材料切削过程中的切削阻力波动较炭质灰岩要低。 这是因为金属材料材料属于韧性材料，在动态切削过程中的力学稳定性较高，切削齿和材料的接触较为稳定，未发生脆性破碎材料接触面积剧烈变化的现象。

3.1 切削力矩结果分析

以潜江-韶关输气管道工程中不同尺寸扩孔器切削砂岩为例，将模拟所获得的切削力矩和传统方法计算所得切削力矩进行比较。 鉴于有限元计算考虑了岩土脆性破碎特征，而理论计算没有考虑，因此可将切削力矩的有限元计算结果与传统理论计算结果之比定义为扩孔器能耗比a。 a值越小，代表岩土脆性对切削过程能耗降低效果越明显。 为了验证有限元模拟切削力矩结果的准确性，可利用能耗比a进行验证。 根据定义，结合岩土的脆性， 能耗比a也等于考虑脆性的切削比能和不考虑脆性的切削比能之比。 砂岩下切削力矩对比结果见表2。

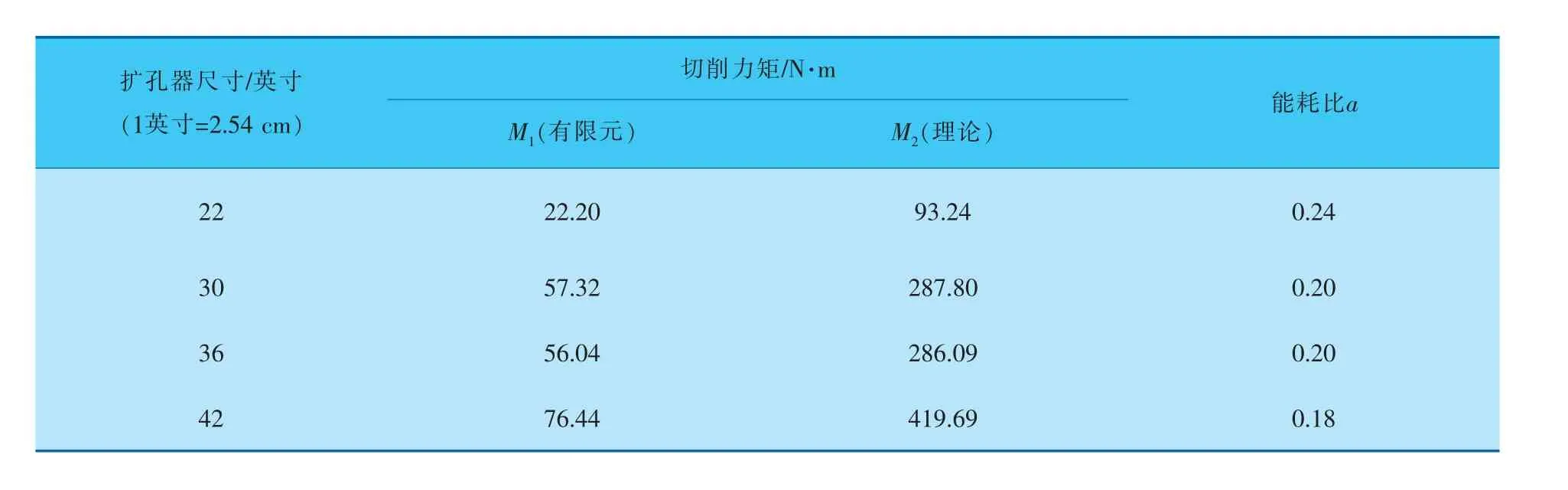
表2 砂岩下切削力矩对比

由表2可以看出， 有限元分析获得的切削力矩比传统理论计算值小很多。 这是由于理论计算未考虑岩土的脆性破坏特征，假设牙轮与岩体完全接触，且岩体强度分布均匀。 而事实上，由于岩土脆性高， 切削过程中和牙轮接触面积不断变化，且远小于理论最大接触面积，切削阻力波动较大。 因此扩孔器如果采用传统理论计算的切削力矩，其切削效率则相对较低。

GOKTAN R M和YILMAZ N G通过实验和数据拟合获得了切削砂岩的比能和脆性指数的关系，其表达式为［4］：

通过式（7）、（8）计算得到本研究所用砂岩的脆性指数B=0.75，比能SEn=0.55 MJ/（m3·MPa）；在不考虑岩土的脆性破碎特征的情况下，岩土脆性指数B=0，比能SEn=2.39 MJ/（m3·MPa）。 两种情况分别对应有限元计算和理论计算结果，将两种情况下的切削比能进行比较，得到能耗比a=0.23。

对表2中不同尺寸扩孔器下的能耗比求平均，得到本研究中砂岩的平均能耗比为0.21，即通过研究发现，考虑岩土脆性后的能耗为不考虑岩土脆性情况下的21%， 与他人实验数据拟合函数的计算结果之间的误差为8.7%，可以验证本研究有限元切削力矩模拟结果的可靠性。

3.2 扩孔器结构参数对切削力矩影响分析

进一步，通过仿真还可探究结构对切削力矩的影响，提出优化方案，达到在保证扩孔效率的前提下，降低切削力矩的目的。

3.2.1 牙轮倾角对切削力矩的影响

在不同的扩孔级别下，通常需要设定扩孔器牙轮倾角，以适应对应级别下的扩孔需求，以潜江-韶关输气管道工程3级扩孔器结构为基准，分析特定工况下不同牙轮倾角对扩孔器切削力矩产生的影响。 考虑牙轮的安装性，牙轮最低倾角为8°，最高倾角为56°。图8为不同牙轮倾角下的扩孔器切削力矩仿真结果。

图8 不同牙轮倾角下的切削力矩

由图8可知，随着牙轮倾角变大，扩孔器所需切削力矩呈上升趋势，由于炭质灰岩的强度高于砂岩的，因此切削灰岩所需力矩大于砂岩，但两者的整体变化趋势大致相同。 扩孔器切削力矩的变化趋势在不同牙轮倾角增长区间内呈现不同的规律，倾角为8°至25°时，扩孔器切削力矩增长趋势较为缓慢；倾角为25°至45°时，切削力矩随倾角增大的趋势开始逐渐变快；倾角为45°至56°时，切削力矩的增长态势明显，在牙轮倾角从8°变为56°的过程中，扩孔器切削力矩的增长率处于上升状态，对倾角变大的敏感度越来越高。 这是由于在工况不变时，被切削岩体在垂直于扩孔方向上的高度是一定的，牙轮倾斜角度越大，和岩体的接触面积越广，切削所需力矩值也就越高，导致扩孔器切削效率降低。 另外，牙轮和岩体的接触面积和切削角度呈倒余弦函数关系，所以在牙轮倾角变化区间内，切削力矩关于倾角的变化率越来越高。 牙轮倾角的增大一方面会使牙轮的安装难度降低，提高安装工艺性；另一方面又会增大切削力矩，降低切削效率，所以工程中可取切削力矩增长趋势缓慢的区间中的最大25°倾角作为最优倾角，兼顾切削力矩和牙轮安装难度两种因数。

3.2.2 切削齿齿深对切削力矩的影响

切削齿作为扩孔过程中直接和岩土发生相互作用的结构，其大小、形状的变化会对孔内岩屑堆积和扩孔器工艺产生较大影响。 分析了牙轮切削齿齿深变化对扩孔器切削力矩的影响， 图9为不同牙轮切削齿齿深下的扩孔器切削力矩变化情况。由图9可知，牙轮齿深越深，所需切削力矩越大， 且切削力矩随齿深变大， 总体呈线性增长趋势。 齿深越深， 牙轮所能切削的岩体深度也越深， 因此所需切削力矩的值随之增高，扩孔器的扩孔速度也会提高。 但是齿深的增大也会给牙轮切削齿和扩孔器钻杆带来较大的负荷， 即增大切削齿的应力和钻杆所受扭矩；另外， 切削齿在实际扩孔工作中会不断磨损，齿深逐渐减小， 会降低切削力矩， 但也影响切削效率和扩孔质量。

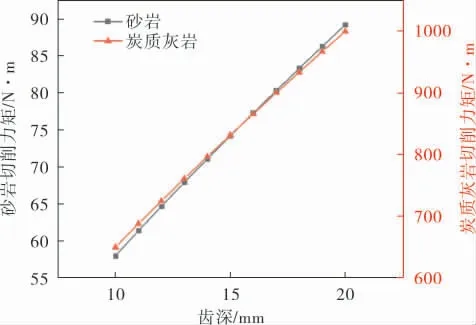
图9 不同齿深下的切削力矩

4 结论

4.1 基于砂岩和炭质灰岩两种岩质，建立了扩孔器和岩土之间相互接触的有限元模型， 对扩孔器切削岩土进行仿真， 发现受脆性影响，岩土材料在切削过程中的切削阻力波动程度远高于金属韧性材料； 计算得到了考虑岩土脆性破碎特征下的扩孔器切削力矩。 通过和理论计算比较， 发现岩土脆性会降低切削力矩和能耗，提高切削效率。 将本研究的平均能耗比和通过他人实验拟合函数计算出的能耗比进行比较，误差在可接受范围内， 验证了切削仿真的可靠性。

4.2 通过分析牙轮倾角对切削力矩的影响，发现在牙轮倾角从8°增为56°的过程中，扩孔器所需切削力矩呈上升趋势， 且力矩的增长率不断提高，切削效率也不断降低，但小牙轮倾角会使牙轮的安装难度增加， 综合安装和切削力矩的问题，可在切削力矩增长趋势缓慢的区间中取最大25°倾角为最优倾角， 在保证切削力矩较小的前提下，降低牙轮安装难度，达到扩孔器结构和工艺上的优化平衡。

4.3 浅切削齿齿深可带来低切削力矩优势，但是切削速度较低，且牙轮耐磨损性能较差，影响成孔质量；加深牙轮切削齿齿深可加深切削岩土深度，提高切削速度，但也会增大扩孔器所需切削力矩，给切削齿和钻杆带来更大的负荷，增大切削齿的应力和钻杆所受扭矩，在扩孔器设计时需综合考虑此结构和工艺上的因数。