(2+1)维四阶非线性方程的解析解

秦立春

(柳州铁道职业技术学院，广西 柳州 545616)

1 引言与研究背景

非线性偏微分方程常用来描述物理定律随时间和空间变化的过程。然而数学物理中的绝大多数用偏微分方程来解释的非线性问题不能通过解析方法求解。精确可解的往往都是常系数和线性的。然而，随着孤子理论的发展，许多求解非线性偏微分方程的方法被提出，比如：三波法、双线性神经网络方法、正二次函数法、tanh函数法、同伦摄动法等等[1-7]。

本文考虑马文秀教授提出的一个(2+1)维四阶非线性方程[8]

γ6utt+γ1uyt+γ5uyy+γ3uxt+γ4uxy+γ2uxx+3αutuxx+3βuyuxx+

3ux(αuxt+βuxy+2uxx)+αuxxxt+βuxxxy+uxxxx=0

(1)

其中u=u(x,y,t)，α，β和γi(i=1,2,…,5,6)均是常数。该方程包含了三种四阶导数项和所有线性二阶导数项的组合。马文秀教授利用正二次函数法获得了方程(1)的两类块状解。方程(1)包含了许多重要的物理模型，比如：

(Ⅰ) 当α=β=0,γ3=-γ5=1,其他的γi均为零，方程(1)约化为一个(2+1)维潜在的Kadomtsev-Petviashvili方程

uxt-uyy+6uxuxx+uxxxx=0

(2)

该方程可以用来描述单层浅层流体中振幅小、对横向坐标依赖慢的长波。

(Ⅱ) 当α=0,β=1,γ3=γ5=1,其他的γi均为零，方程(1)约化为一个广义Bogoyavlensky-Konopelchenko方程

uxxxy+uxt+uyy+6uxuxx+uxxxx+3(uxuy)x=0

(3)

该方程可以用来描述单层浅层流体中振幅小、对横向坐标依赖慢的长波。

当u=2[lnf(x,y,t)]x时，方程(1)将直接变成下列双线性形式

(4)

或

γ5fyy+γ3ftx+γ4fxy+γ2fxx+αfxxxt+βfxxxy+fxxxx)=0

(5)

这样的话，我们只需要求解方程(5)就可以得到方程(1)相应的解析解。

2 解析解

根据三波法，假设

f=e-xτ11-yτ12-tτ13-τ14+exτ11+yτ12+tτ13+τ14δ1+δ2tan(xτ21+yτ22+tτ23+τ24)+

δ3tanh(xτ31+yτ32+tτ33+τ34)

(6)

其中δi和τij(i=1,2,3;j=1,2,3,4)是未知常数。借助Mathematica软件，将该假设代入方程(5)，有

(7)

此时可得方程(1)相应的解析解

(8)

其中f满足方程(6)和(7)。方程(8)的动力学性质被展示在图1。

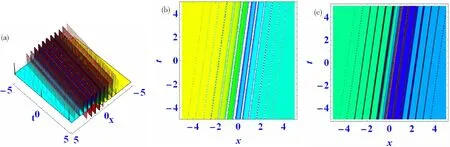
(a)三维图形 (b)等高线图 (c)密度图图1 τ22=τ23=β=2,τ12=τ24=τ34=α=y=1,τ32=-3,τ13=-2,δ1=3,δ2=τ14=δ3=τ33=-1Fig.1 τ22=τ23=β=2,τ12=τ24=τ34=α=y=1,τ32=-3,τ13=-2,δ1=3,δ2=τ14=δ3=τ33=-1

(2)τ31=-βτ32-ατ33,τ21=-βτ22-ατ23,τ11=-βτ12-ατ13,

(9)

此时可得方程(1)相应的解析解

(10)

其中f满足方程(6)和(9)。

(a)三维图形 (b)等高线图 (c)密度图图2 τ22=γ2=β=2,τ12=τ24=τ34=α=y=1,τ32=-3,γ1=γ3=γ4=γ6=-2,τ33=δ2=τ14=δ3=-1,δ1=3Fig.2 τ22=γ2=β=2,τ12=τ24=τ34=α=y=1,τ32=-3,γ1=γ3=γ4=γ6=-2,τ33=δ2=τ14=δ3=-1,δ1=3

(3)τ31=-βτ32-ατ33,τ21=-βτ22-ατ23,τ11=-βτ12-ατ13,

(11)

此时可得方程(1)相应的解析解

(12)

其中f满足方程(6)和(11)。方程(12)的动力学性质被展示在图2和图3。

(a)三维图形 (b)等高线图 (c)密度图图3 τ22=γ2=β=2,τ12=τ24=τ34=α=t=1,τ32=-3,γ1=γ3=γ4=γ6=-2,τ33=δ2=τ14=δ3=-1,δ1=3Fig.3:τ22=γ2=β=2,τ12=τ24=τ34=α=t=1,τ32=-3,γ1=γ3=γ4=γ6=-2,τ33=δ2=τ14=δ3=-1,δ1=3

(13)

此时可得方程(1)相应的解析解

(14)

其中f满足方程(6)和(13)。

(15)

此时可得方程(1)相应的解析解

(16)

其中f满足方程(6)和(15)。

(17)

此时可得方程(1)相应的解析解

(18)

其中f满足方程(6)和(17)。

(7)δ1=0,τ31=-βτ32-ατ33,τ21=-βτ22-ατ23,γ5=-β2γ2+βγ4,

τ11=-βτ12-ατ13,γ6=α(-αγ2+γ3),γ1=-2αβγ2+βγ3+αγ4

(19)

此时可得方程(1)相应的解析解

(20)

其中f满足方程(6)和(19)。

(21)

此时可得方程(1)相应的解析解

(22)

其中f满足方程(6)和(21)。

(23)

此时可得方程(1)相应的解析解

(24)

其中f满足方程(6)和(23)。

3 结论

最近，马文秀教授提出了一个新的(2+1)维四阶非线性偏微分方程。该方程考虑了所有的线性二阶导数项，包含了Kadomtsev-Petviashvili方程和广义Bogoyavlensky-Konopelchenko方程等物理模型，可以用来描述单层浅层流体中振幅小、对横向坐标依赖慢的长波。本文利用三波法和Mathematica软件获得了新的(2+1)维四阶非线性偏微分方程大量的解析解，这些解含有丰富的动力学性质。从求解过程中可以看出三波法求解解析解是非常简单方便的，能够用于很多其他的高阶非线性偏微分方程。