融合高阶路径和非负矩阵分解的链路预测

陈广福 陈 浩

(1. 武夷学院 数学与计算机学院， 福建 武夷山 354300；2. 认知计算与智能信息处理福建省高校重点实验室， 福建 武夷山 354300；3. 江苏大学京江学院 电子信息工程学院， 江苏 镇江 212013)

0 前 言

现实世界中存在大量的复杂系统，如交通运输系统、生物系统和电力系统等。为刻画和研究抽象的复杂系统，常使用复杂网络对其进行描述，其中节点表示实体，链接表示实体间的交互关系。如何分析和挖掘复杂网络是网络科学的研究热点之一，而链路预测为分析和挖掘复杂网络提供了重要的理论支持。链路预测的目的是根据已知结构信息来预测缺失链接或将来形成连边的可能性[1]。链路预测在多种领域有着广泛的应用价值，如预测新增航线[2]、提供完整的中医药知识图谱[3]和药物组合推荐[4]。

加权网络广泛存在于现实世界中，但不同加权网络中的链接权重蕴含着不同含义，如用户信任/不信任网络中的正链接权重表示信任，在二部图语言网络中的链接权重代表给定语言和国家的人口比例。因此，链接权重用来表示加权网络中节点间链接的强弱关系。目前，大部分链路预测的研究仅针对无向无权网络，忽略了链接权重信息，因此如何捕获链接权重信息是值得思考的问题。一些研究人员开始探索加权网络的链路预测问题。学者们将共同邻居(common neighbors，CN)、资源分配(resource allocation，RA)和adamic-adar(AA)等指标与加权社交网络融合构建为加权共同邻居(weighted common neighbors，WCN)、加权资源分配(weighted resource allocation，WRA)和加权adamic-adar(weighted adamic-adar，WAA)[5-8]。De等人将局部路径(local path，LP)扩展到加权网络，考虑二阶和三阶边权强度，构建加权局部路径(weigthed local path，WLP)[9]。Zhu等人将加权互信息(weighted mutual information，WMI)与WCN、WAA和WRA等3个局部指标融合构建为WMIWCN、WMIWAA和WMIWRA，以保持自然权重和局部结构信息[10]。郭景峰等人考虑了加权网络二阶和三阶路径信息，提高了预测准确度[11]。袁榕等人提出基于耦合边聚类和扩散性的拓扑权重链路预测框架，提高了预测精度[12]。傅馨玉等人通过耦合加权局部相似度指标(WCN、WAA和WRA)与节点重要性特征(度中心性、介数中心性、接近中心性和特征向量中心性)，构建适用于小型加权网络的预测指标[13]。

Wind等人首次利用非负矩阵分解的低秩性和非负性等特点构建模型，以预测缺失链接权重[14]。Pech 等人利用线性优化(linear optimization，LO)指标，对节点三阶路径求解最优值[15]。Chen等人基于加权非负矩阵分解框架融合自然权重和节点聚类[16]。上述加权预测指标都只考虑了自然权重和局部结构信息，而忽略了全局结构信息的重要性。为此，本次研究提出了融合高阶路径和非负矩阵分解的链路预测模型(nonnegative matrix factorization via high-order path，NMF-HP)。

1 方法

1.1 相关概念

给定一个不考虑自环链接的无向加权网络G(V,E,W)，其中V表示网络节点集；E={(vi,vj)|vi,vj∈V}，表示节点间链接集；W表示链接权重集。A表示G的邻接矩阵，A=[aij]n×n，如果节点vi和vj之间存在链接，则aij=wij，否则aij=0。

为了验证模型性能，将可观测链接集E随机划分为训练集ET和测试集EP，ET∩EP=φ，ET∪EP=E。

1.2 加权网络高阶路径

权重结构是加权网络的重要特征，如何捕获权重结构是加权网络链路预测的关键一环。本次研究通过计算链接权重强度来获取并扩展节点二阶路径信息，以保持高阶路径信息。节点强度是加权网络的基本拓扑信息，反映节点与邻居之间的关联强度，节点强度越大，节点邻域权重占加权网络权重的比例越大。

计算加权网络任意节点vi的权重强度Si，如式(1)所示：

(1)

式中：ni—— 节点vi的邻域集；

wij—— 节点vi和vj的权重。

利用链接权重强度(link weighted strength，LWS)衡量加权网络的局部相似度，LWS越大，节点相似的可能性越高。LWS的计算如式(2)所示:

(2)

将式(2)扩展成任意节点的k阶相似度，如式(3)所示：

(3)

本次研究仅考虑k=2和k= 3的情况，通过融合二阶和三阶路径来构建最终相似度[17]，以同时保持权重局部和全局结构，如式(4)所示：

(4)

1.3 NMF-HP链路预测模型构建

非负矩阵分解能够有效捕获原始网络的链接权重。设任意加权网络邻接矩阵A的损失函数如式(5)所示：

(5)

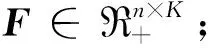
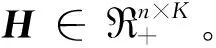
由于式(5)仅能捕获原始网络自然权重链接而无法捕获加权网络结构，因此将图正则化技术与式(4)相融合，同时保持权重拓扑结构。

设hi和hj是任意节点的特征向量，如式(6)所示：

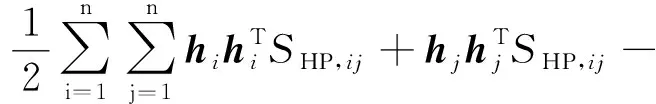
=tr(HTDH)-tr(HTSH)

=tr(HTLH)

(6)

式中：tr() —— 矩阵迹；

D—— 对角矩阵；

L——S的拉普拉斯矩阵，L=D-S。

耦合式(5)和式(6)，构建统一链路预测模型，模型损失函数如式(7)所示：

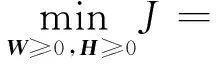
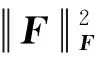
(7)

式中：α—— 控制局部和高阶路径权重的参数；

β—— 约束因子，用于预防模型过度拟合。

为学习模型参数，使用拉格朗日乘法规则求解模型最优解，重写式(7)得到：

J(F,H)=tr(AAT-2AFHT+FHTHFT)+

αtr(HTLH)+βtr(HTH)+

βtr(FTF)

(8)

引入拉格朗日乘子矩阵Φ=(φnk)和Ψ=(ψnk)，重写式(8)得到：

J(F,H)=tr(AAT-2AFHT+FHTHFT)+

αtr(HTLH)+βtr(HTH)+βtr(FTF)+

tr(ΦHT)+tr(ΨFT)

(9)

(1) 固定F,更新H。

首先, 删除式(9)中与H无关项,得到：

J(H)=tr(-2AFHT+FHTHFT)+αtr(HTLH)+βtr(HTH)+tr(ΦHT)

(10)

其次，对式(10)求偏导得到：

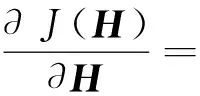
βH+Φ

(11)

然后，根据 KKT(karush-kuhn-tucker)条件且φnkhnk=0，得到：

-AF+HFTF-α(D-S)H+βH=0

(12)

最后,得到以下更新规则：

(13)

(2) 固定H,更新F。

首先，删除式(9)中与F无关项,得到：

J(F)=tr(-2AFHT+FHTHFT)+

βtr(FTF)+tr(ΨFT)

(14)

其次，对式(14)求偏导得到：

(15)

然后，根据 KKT条件且ψnkfnk=0，得到：

-ATH+FHTH+βF=0

(16)

最后，得到以下更新规则:

(17)

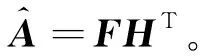
2 实验结果分析

2.1 评价度量

(1) AUC(areas under curve)[17]是ROC曲线与坐标轴围成的面积，AUC的计算如式(18)所示：

(18)

式中：Auc—— AUC；

n—— 比较次数；

n1—— 测试集中节点分数大于不存在集中节点分数的次数；

n2—— 测试集中节点分数等于不存在集中节点分数的次数。

(2) PCC(pearson correlation coefficient)[18]用于评价预测向量和实际向量的线性关系，PCC的计算如式(19)所示：

(19)

式中：CPC—— PCC；

wij—— 预测向量；

rij—— 实际向量；

(3) 精确度(Precision)[19]仅考虑前M个链接是否预测准确，若有m个链接属于测试集，则精确度的计算如式(20)所示：

(20)

式中：P—— 精确度。

2.2 数据集

本次研究选取6个加权网络来测试NMF-HP模型性能。论坛网络(FORUM)包括899个用户和522个主题，节点表示用户，链接权重表示交换信息数量；食物网络(BAYdry，BAY)是由128个节点和2 106条链接构成的干旱季节南佛罗里达州柏树湿地的碳交换食物网；美国航空运输网络(USAir，USA)中的节点和链接分别代表机场和路线，链接权重表示航班数量；秀丽隐杆线虫网络(CELegans，CEL)包括297个节点和2 148条链接，节点表示神经元，链接表示突触联系，链接权重表示2个神经元之间的突触数量；生物网1(CEGN)包括2 219个节点和107 352条链接，节点表示基因，链接权重表示细菌和古细菌直系同源基因的领域关联程度；生物网2(SCLC)包括2 003个节点和40 898条链接，节点表示蛋白质，链接权重表示中小型蛋白质的相互作用[20]。

2.3 基准方法

本次研究选取9个主流的加权网络链路预测方法与NMF-HP模型进行对比分析。

(1) 基于加权局部相似度的链路预测。WCN、WAA、WRA[5]的定义如式(21)所示：

(21)

式中：z∈Oxy表示节点x和y的共同邻居。

(2) 基于互信息和加权局部结构相似度耦合的链路预测。WMIWCN、WMIWAA和WMIWRA[9]的定义如式(22)所示：

(22)

式中：I(Lxy;z) —— 节点x和y的共同邻居互信息。

(3) 加权优先连接(weigthed preferential attachment，WPA)[11]是任意节点乘积度，其定义如式(23)所示：

(23)

式中：Γ(x)表示节点x的邻居集。

(4) 加权局部路径(weigthed local path，WLP)[11]融合了加权网络二阶和三阶路径信息，其定义如式(24)所示：

(24)

式中：γ—— 超级参数；

l—— 路径长度。

(5) 线性优化(linear optimization，LO)[15]通过相邻节点贡献的线性最优化计算节点未链接相似度，其定义如式(25)所示：

SL0=αA(αATA+I)-1ATA

(25)

2.4 实验结果分析

NMF-HP模型包括4个重要参数：α、β、迭代次数和K。设α=5，β=0.5，K=70，迭代次数为70。利用AUC、PCC和Precision度量来评价基准指标和NMF-HP模型性能。由实验结果(见表1、图1和图2)可知：

图1 不同方法在加权网络上的PCC值

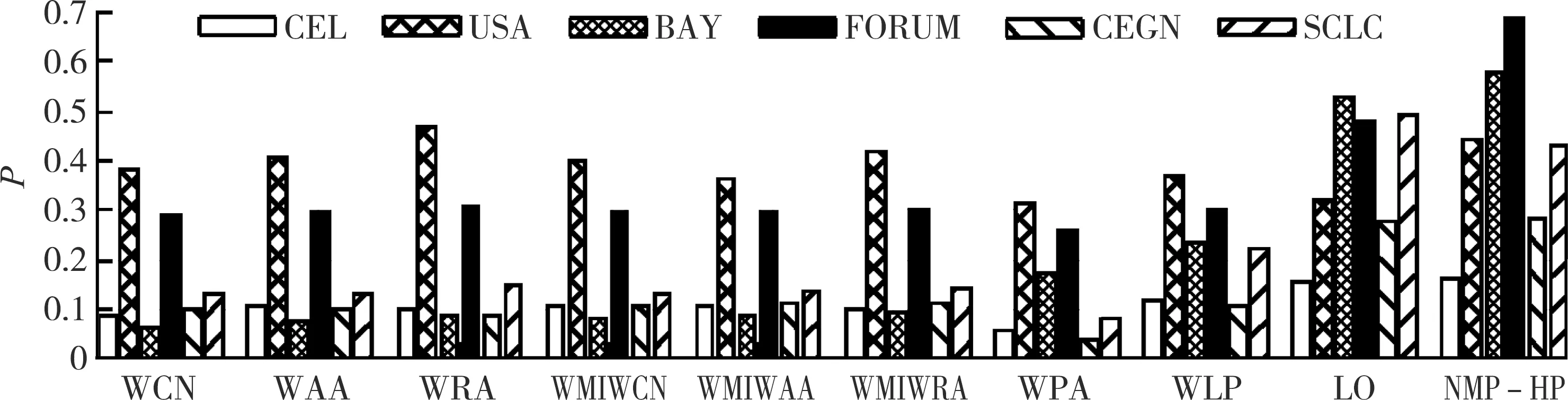
图2 不同方法在加权网络上的Precision值

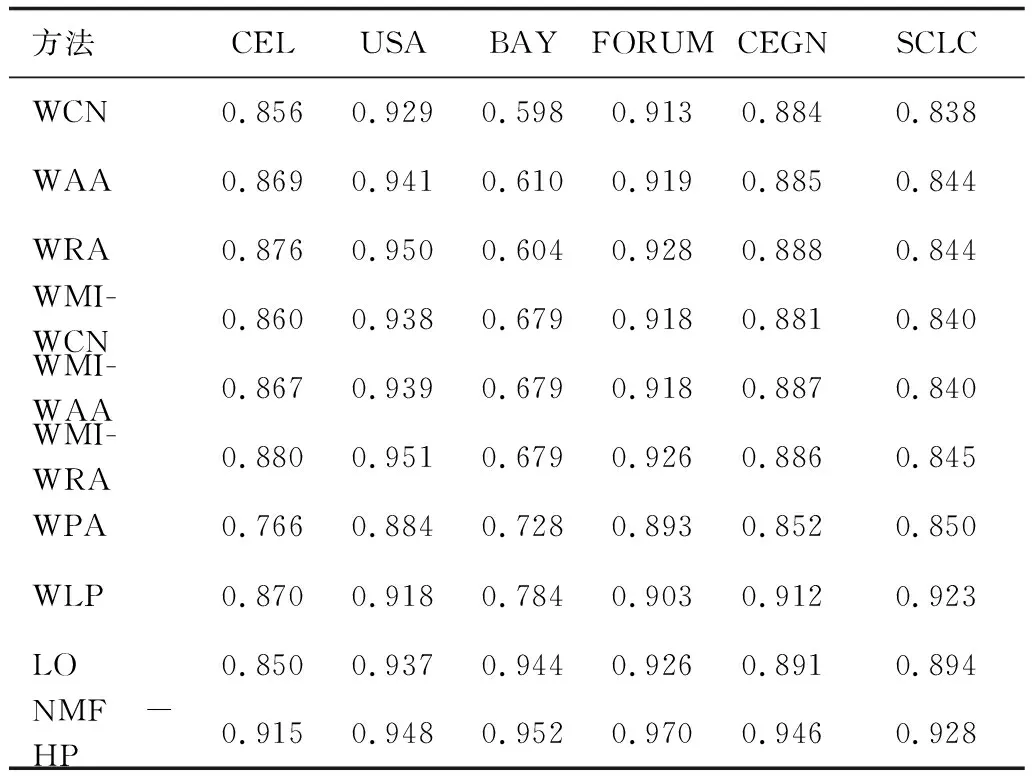
表1 不同方法在加权网络上的AUC值

(1) AUC度量，NMF-HP模型在除USA之外的5个加权网络上均获得了最优预测准确度；NMF-HP模型在CEL上的AUC值比WMIWRA提高了3.9%，在BAY上的AUC值比LO提高了0.9%，在FORUM上的AUC值比WRA提高了4.5%，在CEGN和SCLC上的AUC值分别比WLP提高了3.7%和0.5%。PCC度量，NMF-HP模型在CEL、BAY、CEGN和SCLC上的PCC值分别比LO提高了24.0%、12.6%、10.4%和14.7%，在FORUM上的PCC值比WMIWAA提高了51.8%。Precision度量，NMF-HP模型在CEL、BAY、FORUM和CEGN上的Precision值分别比LO提高了3.8%、10.2%、42.8%和4.3%。

(2) WCN、WAA和WRA仅考虑了网络链接权重信息，在大部分加权网络上的预测准确度较低，主要原因在于其只获得了部分网络结构信息。WMIWCN、WMIWAA和WMIWRA在CEL和BAY上的预测准确度优于WCN、WAA和WRA，主要原因在于其同时考虑了自然权重和加权局部结构。

(3) WLP和LO考虑了三阶路径信息，在BAY、CEGN和SCLC上的预测准确度显著高于其他基准方法。NMF-HP模型考虑了多路径信息，其AUC和PCC值显著高于WLP和LO，表明考虑多路径信息的加权网络性能优于二阶或三阶路径。

(4) PCC用来衡量实际链接权重与预测权重间的线性关系。PCC值越大，预测权重越接近实际权重。NMF-HP模型在大部分加权网络上获得了最优性能，表明融合自然权重和高阶路径信息的网络更接近于原始网络。

由于篇幅有限，在此仅利用AUC来测试NMF-HP模型的鲁棒性。由实验结果(见图3)可知，NMF-HP模型在不同的训练集占比下均能获得最优性能，表明附加高阶路径信息可以捕获足够的网络结构，并对稀疏网络具有鲁棒性。其他基准方法在不同的训练集占比下波动明显，表明仅依靠网络自然权重和局部结构是不够的，尤其是当训练集占比为40%～50%时，缺失链接占比达到50%～60%，在网络十分稀疏的情况下NMF-HP模型的AUC值优于其他基准方法。

图3 不同训练集占比下的AUC值

3 参数敏感性分析

NMF-HP模型通过调节α、β、K和迭代次数等4个参数来获得最优预测精度。设α、β的取值范围为{0，0.05，0.5， 5，50，500}，K的取值范围为{10，20，30，…，100}，迭代次数的取值范围为{10，20，30，…，100}。由于篇幅有限，在此仅分析AUC度量随参数的变化情况。

3.1 参数α的变化

参数α是控制二阶路径和三阶路径权重的贡献，不同参数α下的AUC值如图4所示。当α=0时，NMF-HP模型退化为非负矩阵分解基础模型和预防过度拟合的正则化项，在6个加权网络上的预测准确度较低，进一步说明融合二阶路径和三阶路径信息的必要性。AUC值随着α的增加而增加，直到α=5时，AUC值最大。当α>5时，AUC值开始逐渐下降，表明α取较大值会影响NMF-HP模型捕获多路径信息。因此，当α=5时，NMF-HP模型性能最优。

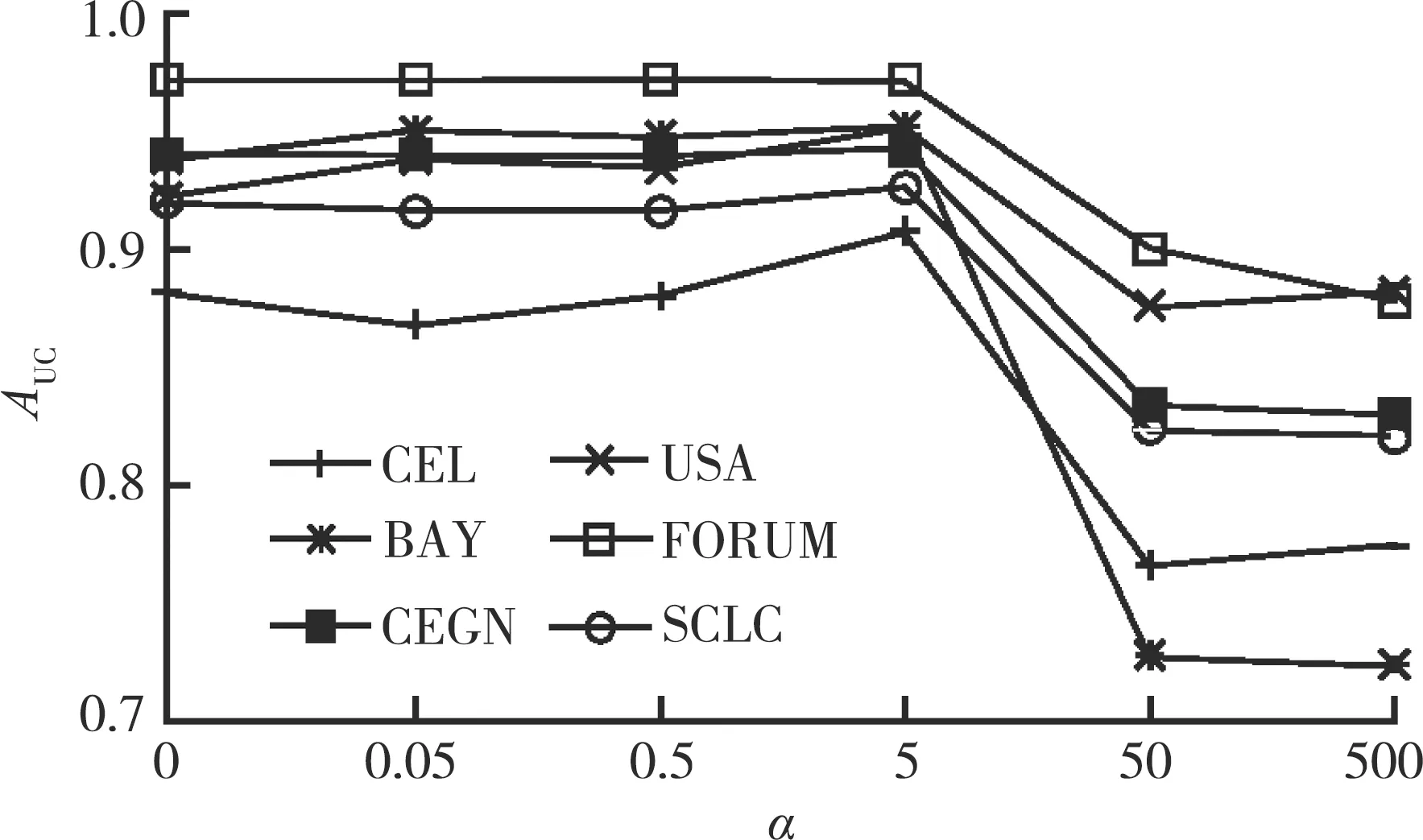
图4 不同参数α值下的AUC值

3.2 参数β的变化

参数β用于防止NMF-HP模型过度拟合，不同参数β下的AUC值如图5所示。当β=0时，NMF-HP模型退化为非负矩阵分解基础模型和多阶路径信息，在6个加权网络上的预测准确度较低，表明NMF-HP模型存在过度拟合。AUC值随着β的增加而增加，直到β=0.5时，AUC值最大。当β>0.5时，AUC值开始逐渐下降，表明β取较大值时无法有效抑制过度拟合。因此，当β=0.5时，NMF-HP模型性能最优。

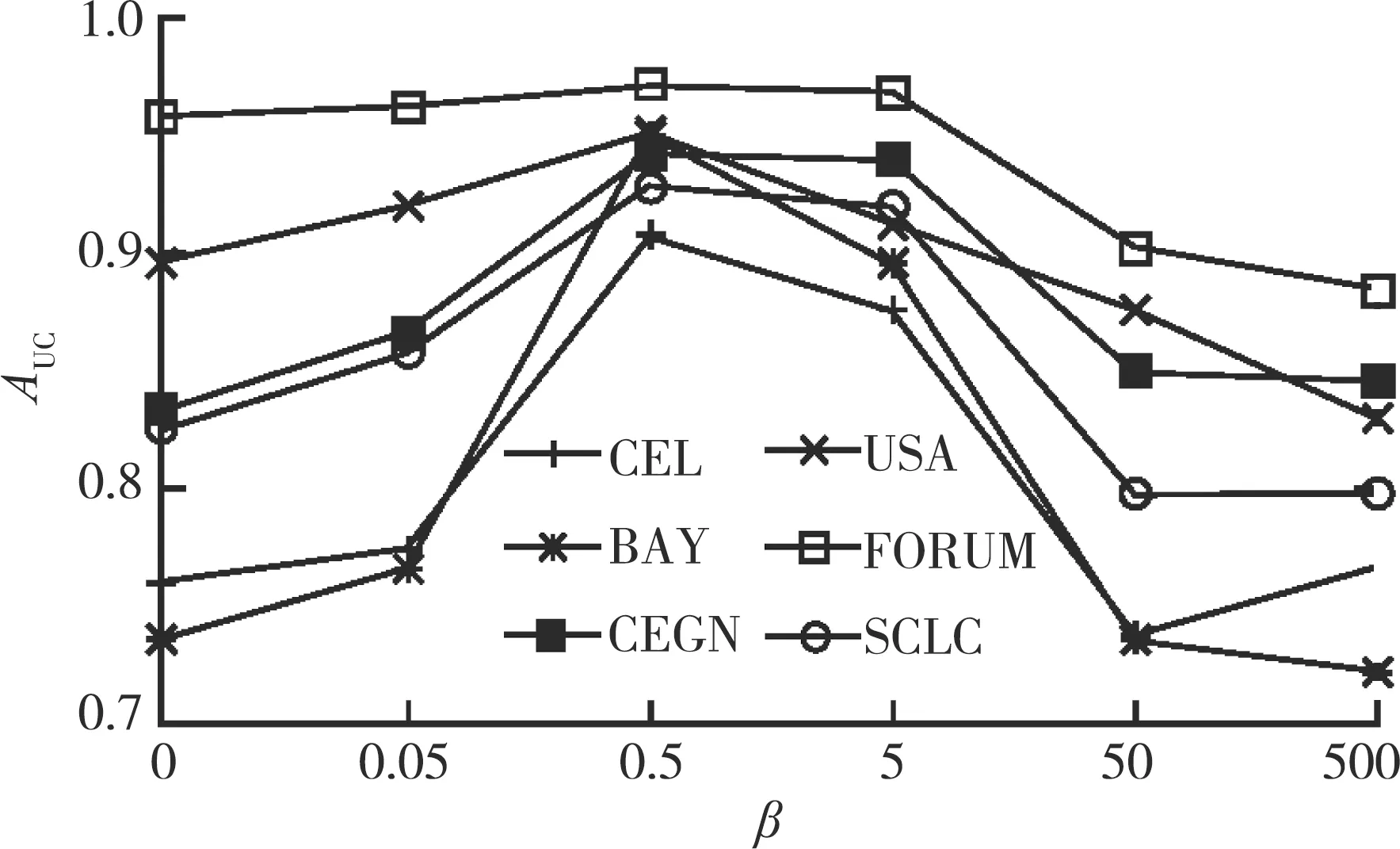
图5 不同参数β值下的AUC值

3.3 参数K的变化

参数K的变化直接影响着NMF-HP模型性能，不同参数K下的AUC值如图6所示。当K=10时，AUC值最小，表明潜在空间较小的情况下NMF-HP模型无法挖掘更多网络结构。当K逐渐增加时， AUC值开始上升，直到K≥70时，AUC值趋于稳定。因此，当K=70时，NMF-HP模型性能最优。

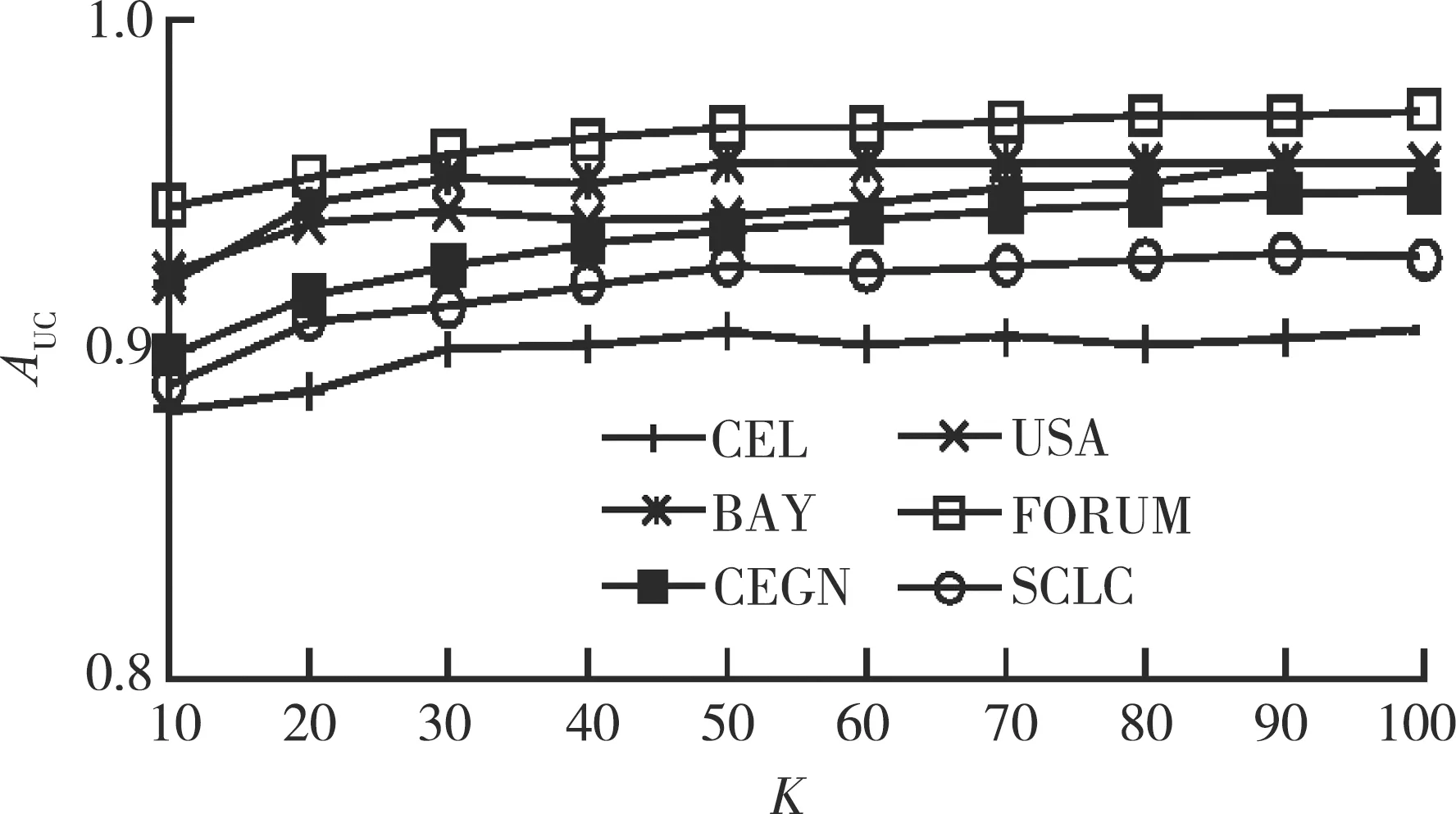
图6 不同参数K值下的AUC值

3.4 迭代次数的变化

迭代次数的大小直接影响着NMF-HP模型的预测精度，迭代次数过大会导致运行时间增加、预测精度下降，不同迭代次数下的AUC值如图7所示。当迭代次数为10时，AUC值最小，表明迭代次数过小不利于捕获多阶节点路径信息。随着迭代次数的增加，AUC值开始逐渐上升，直到迭代次数大于70时，AUC值开始保持稳定。因此，当迭代次数为70时，NMF-HP模型性能最优。

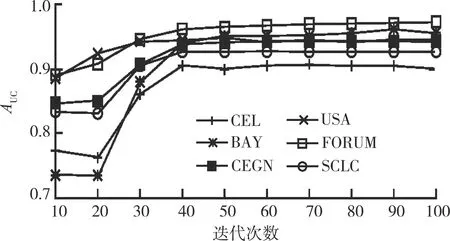
图7 不同迭代次数下的AUC值

4 结 语

本次研究提出了融合高阶路径和非负矩阵分解的链路预测。首先，根据加权网络点强度计算边权强度，以保持加权网络局部结构；其次，将任意加权网络邻接矩阵映射到低秩隐特征空间，以捕获一阶权重链接；然后，扩展加权强度为二阶路径和三阶路径信息，采用图正则化技术融合多阶路径信息，同时保持网络局部和全局结构，并通过更新规则学习模型参数；最后，通过实验证明NMF-HP模型性能优于现有的主流基准方法。