基于平移约束的异质超网络表示学习

刘贞国，朱 宇，赵海兴，王晓英，黄建强

(1. 青海大学 计算机技术与应用系，青海 西宁810000； 2. 青海师范大学 藏语智能信息处理及应用国家重点实验室，青海 西宁810000)

0 引言

网络表示学习[1]将网络中的每个节点映射到一个低维的向量表示空间，学习到的节点表示向量可以被用于网络分析任务，例如，节点分类[2]、链接预测[3]、社区检测[4]等。目前，超网络表示学习逐渐受到研究者的广泛研究。根据超网络表示学习方法[5]的特点，将其划分为展开式谱分析方法和非展开式方法。展开式谱分析方法将超网络转化为普通网络来学习节点表示向量。例如，星型扩展和团扩展[6]，该类方法在超网络展开过程中会丢失超边信息。非展开式方法，没有分解超边，具体来说，该类方法主要分为非展开式谱分析方法和基于神经网络的方法。例如，Hyper2vec[7]、HPSG[8]、HPHG[8]、DHNE[9]等。

从以上两类工作可以看出，展开式谱分析方法虽然直观灵活，但是存在信息损失。非展开式方法没有分解超边。例如，Hyper2vec、HPSG通过Skip-gram[10]模型捕获基于超边游走序列上的节点成对关系，但是没有很好地捕获节点之间的元组关系。HPHG通过Hyper-gram模型有效地捕获了元组关系。DHNE通过结合多层感知器来捕获元组关系，但是HPHG和DHNE均局限于固定大小的异质超边。

受到上述方法的启发，为了应对复杂的超网络结构，同时捕获节点之间的成对关系和元组关系，本文提出了一种基于平移约束的异质超网络表示学习方法HRTC。

本文的贡献主要有如下两个方面：

(1) 由于超网络结构复杂，首先提出一种结合团扩展和星型扩展的方法，将异质超网络转换为异质网络[11]；然后，提出感知节点语义相关性的元路径游走方法来捕获异质节点之间的语义关系；最后，通过引入知识表示学习中的平移机制，在基于拓扑派生目标函数的模型上融入超边，提出基于平移约束的异质超网络表示学习方法HRTC，该方法可以同时捕获节点之间的成对关系和元组关系。

(2) 在三个不同类型的超网络数据集上进行了评估实验。实验结果表明，HRTC方法在链接预测和超网络重建任务中，效果优于其他基线方法。

本文组织结构如下： 第1节正式定义了研究问题；第2节介绍预备知识；第3节详细介绍HRTC方法；实验结果见第4节；最后总结全文。

1 问题定义

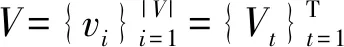
图1 异质超图

定义1(异质超网络表示学习)给定一个异质超网络H=(V，E)，异质超网络表示学习为异质超网络的每个节点vi∈V学习一个低维向量rvi∈Rk，其中，k≪ |V|。其目的是使得学习到的向量显式地保留异质超网络结构信息，并且在异质超网络结构中相邻的节点在向量表示空间中也相邻。

2 预备知识

2.1 超图转化为普通图

超图是图的推广，图是超图的特例。由于对图的研究比较成熟，如果能把超图转化为图，通过对图的研究加深对相应超图的认识，不失为研究超图的一种可取的方法。文献[12]分别通过团扩展和星型扩展，将超图转化为2-截图和关联图。

超图转化为2-截图、关联图的详细策略如下：

2.1.1 2-截图

超图H=(V，E)的2-截图(2-section graph)是满足以下条件的图S=(V′，E′)：

(1)V′=V，即S的节点集合与H的节点集合相同；

(2) 任意两个不同的节点之间连一条边，当且仅当它们同时包含在H的至少一条超边中。

图2是图1超图的2-截图。

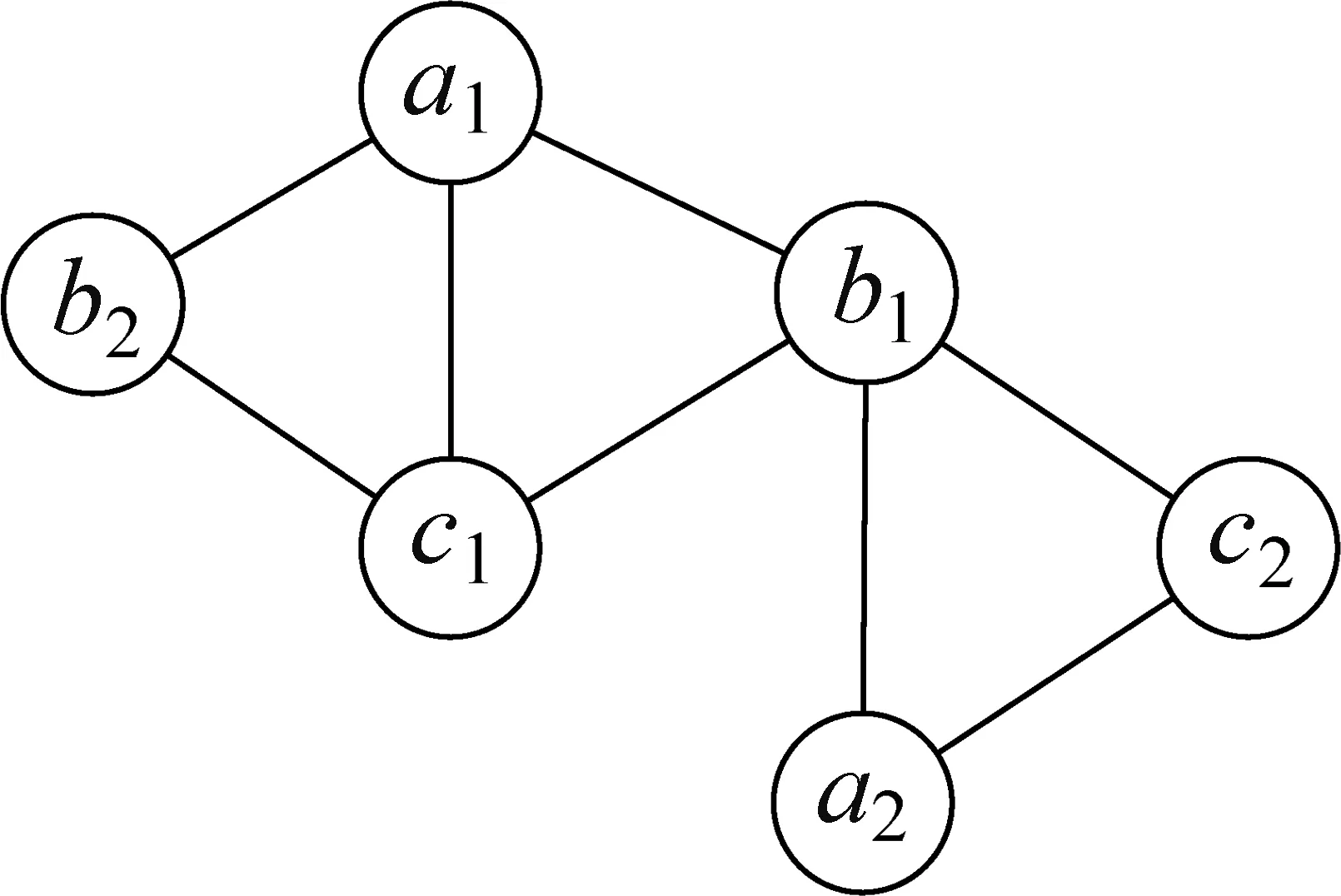
图2 2-截图

2.1.2 关联图

超图H=(V，E)的关联图是满足以下条件的图I=(V′，E′)：

(1)V′=V∪E，即将超图H中的每条超边看成一个节点，I的节点集合是H的节点集合和超边集合的并集；

(2)vi∈V和ei∈E相邻，当且仅当vi∈ei。

图3为图1超图的关联图，其中e节点为超边节点。

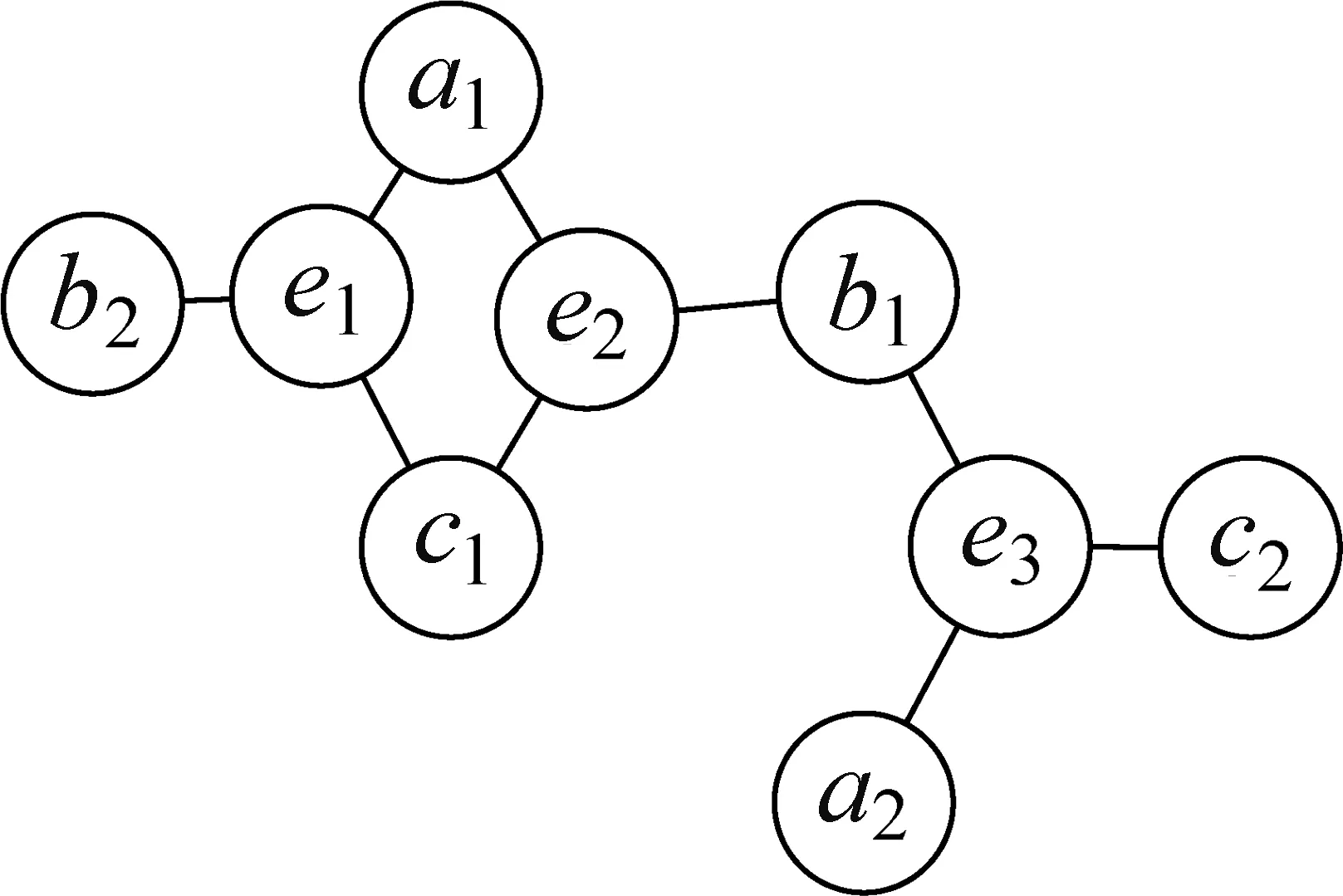
图3 关联图

2.2 TransE模型

知识表示实际上是让知识图谱的实体和关系向量化。具体地说，为知识库中的每一个实体或关系学习一个低维向量。为了简化起见，使用(h，r，t)表示三元组，其中，h表示头实体向量，r表示关系向量，t表示尾实体向量，在知识图谱的关系抽取中，经常采用基于平移的知识表示学习模型TransE[13]。该模型认为，如果存在一个正确的三元组(h，r，t)，则头实体向量h加上关系向量r约等于尾实体向量t，即h+r≈t。否则，其向量之间不满足这种关系。TransE模型如图4所示。

图4 TransE模型

3 HRTC方法

HRTC方法的框架如图5所示。该框架包括4个主要部分： (a)2-截图+关联图； (b)感知节点语义相关性的元路径游走SRwalk； (c)基于拓扑派生目标函数的模型； (d)基于平移约束目标函数的模型。下面详细介绍HRTC方法的4个主要部分。

图5 HRTC框架

其中，Ev和θv分别表示嵌入矩阵和参数向量，ev、eh、er分别为v、h、r对应的向量且eh+r=eh+er，其中，超边r同时与目标节点v和节点h关联，图5(a)、(b)、(c)、(d)分别为该框架的4个主要部分。

3.1 2-截图+关联图

团扩展方法认为超边内部节点之间两两相关，将超图转换为2-截图。星型扩展方法认为超边内部节点之间两两不相关，将超图转换为关联图。因此，在异质超网络表示学习过程中应用团扩展方法和星型扩展方法都会导致不同程度的超网络结构信息损失。

鉴于上述情况，本文提出一种结合团扩展和星型扩展的方法，将超图转换为2-截图+关联图。具体来说，通过分析超边内部节点之间的语义相关性，认为具有语义相关性的节点之间直接关联，不具有语义相关性的节点通过超边间接关联。节点语义相关性的定义如下。

定义2(节点语义相关性)节点代表的实体对象之间存在关系。

元组节点之间具有语义相关性，而元组子集节点之间可能不具有语义相关性。例如，若图1为drug药物超网络，则图6为图1转换后的2-截图+关联图，其中a，b，c分别代表用户节点、药物节点和不良反应节点，则元组关系(用户，药物，反应)被看作超边来构建超网络。具体来说，在没有药物信息的情况下建立用户与不良反应之间的联系和在没有药物不良反应信息的情况下建立用户与药物之间的联系都是不合理的，所以用户与不良反应、用户与药物被认为语义不相关。然而，对于每种药物，都会在出厂标明一种或几种特定的不良反应，所以药物与不良反应被认为语义相关，则药物节点与不良反应节点之间直接关联，而用户节点与药物节点、用户节点与不良反应节点之间通过超边间接关联。

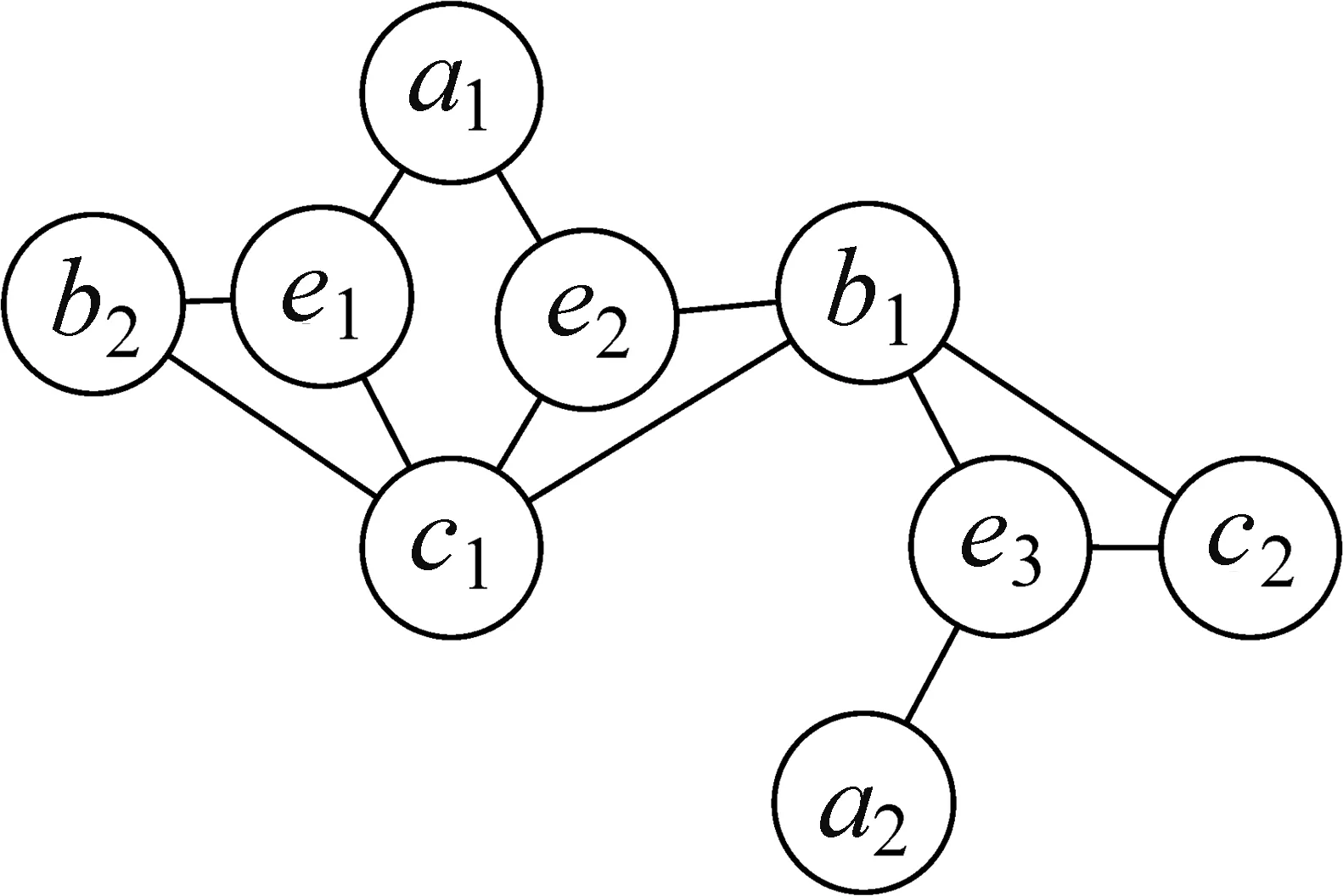
图6 2-截图+关联图

总之，如果超边内部节点之间两两语义相关，则2-截图+关联图为完全组合图；如果超边内部节点之间全部语义不相关，则2-截图+关联图退化为关联图；如果超边内部部分节点之间存在语义相关，则2-截图+关联图为在关联图基础上加上具有语义相关性节点的边。

超图转换为2-截图+关联图的实现细节如算法1所示。

算法1 超图转换为2-截图+关联图输入: 异质超图H=(V,E);输出: 2-截图+关联图的邻接矩阵A(|V|+|E|)×(|V|+|E|);/∗将异质超图H作为输入,获取2-截图+关联图的邻接矩阵A(|V|+|E|)×(|V|+|E|),其中,A的元素初始化为0∗/ 1. for e in E do 2. for vi in e do 3 . for vj in e do 4. if vi和vj语义相关 do 5. A(vi,vj)=A(vj,vi)=1 6. else 7. A(vi,e)=A(e,vi)=A(vj,e)=A(e,vj)=1 8. end for 9. end for 10. end for 11. return A

3.2 感知节点语义相关性的元路径游走SRwalk

对于上述转换后的异质网络G=(V，E)，设计一种感知节点语义相关性的元路径游走方法SRwalk来捕获节点之间的语义关系，即成对关系和元组关系。下面给出元路径的定义。

(1)

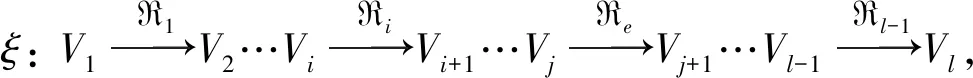
与传统随机游走相比，SRwalk可以更好地保留超网络中节点之间的元组关系和增强节点之间的成对关系。如图7中的游走序列，a1-e2-b1-c1和c1-b2-e1-a1这种子序列可以高可信度地捕获节点之间的元组关系，如(a1，b1，c1)和(a1，b2，c1)，而且增强了b1和b2之间的相关性。

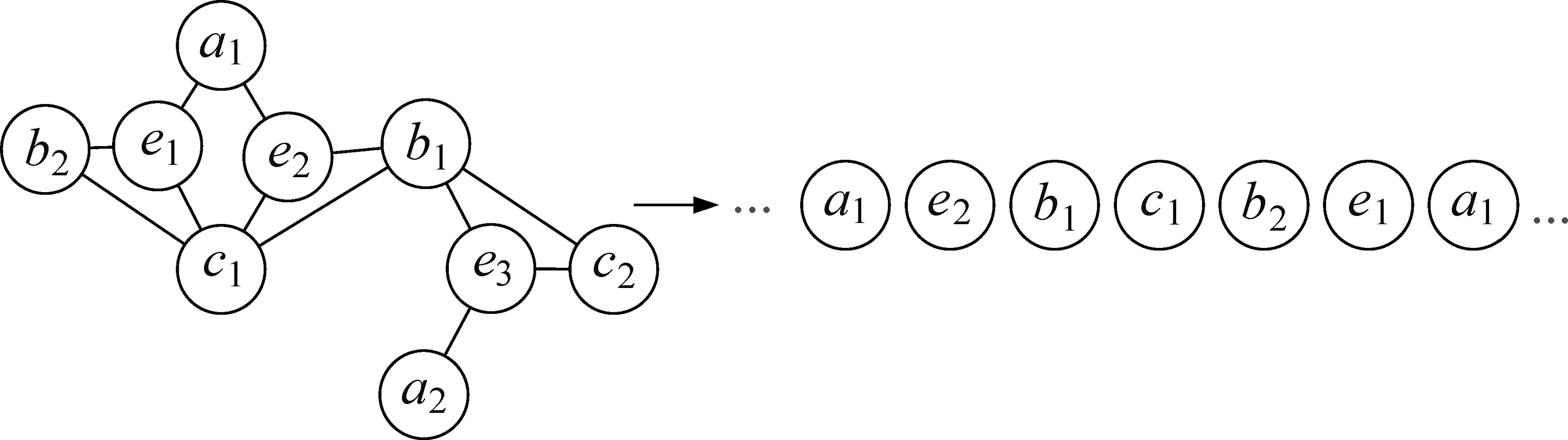
图7 感知节点语义相关性的元路径游走

SRwalk方法的实现细节如算法2所示。

算法2 SRwalk方法输入: 2-截图+关联图的邻接矩阵A;采样次数N和采样长度L;输出: 感知节点语义相关性的元路径游走序列paths;/∗采用感知节点语义相关性的元路径游走ξ: V1R1→V2…ViRi→Vi+1…VjRe→Vj+1…Vl-1Rl-1→Vl来采样异质序列,∗/ 1. for n in range (1,N+1) do 2. for v in V1 3. 按照ξ由v开始遍历A,采样长度L的异质序列path 4. 将path添加到paths中 5. end for 6. end for 7. return paths

3.3 拓扑派生目标函数

基于SRwalk获取的异质节点序列C，提出了拓扑派生目标函数来捕获节点成对关系。下面详细介绍拓扑派生目标函数。

对于目标节点v∈C，当v的上下文节点为c∈context(v)时，将c视为正样本，将非上下文节点Neg(v)视为负样本。节点的标签定义如式(2)所示。

(2)

p(u|v)表示在已知目标节点v的条件下预测其上下文节点u的概率。对于给定节点序列C，拓扑派生目标函数如式(3)所示。

(3)

对于每一个节点v，嵌入向量ev是v作为目标节点的表示向量，参数向量θv是v作为上下文节点时的表示向量。则式(3)中的p(u|v)定义如式(4)所示。

(4)

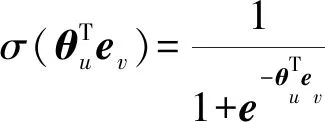
(5)

因此，公式L1重新表示如式(6)所示。

(6)

最大化L1意味着同时最大化正样本的预测概率和最小化负样本的预测概率。通过捕获节点成对关系，将超网络拓扑结构编码到节点向量表示中。

3.4 平移约束目标函数

虽然最大化拓扑派生目标函数可以捕获节点成对关系，但是没有充分考虑超边。因此，鉴于上述情况，受到TransE模型中的平移机制在知识表示中成功应用的启发，将超网络中节点之间的交互看作节点表示向量通过超边表示向量进行的平移操作。通过引入平移机制为目标节点增加超边约束来捕获节点之间的元组关系。下面详细介绍平移约束目标函数。

具体来说，对于目标节点v∈V，Rv是与v关联的超边集合，Hr是与v具有关系r的节点集合。如果存在超边r∈Rv和节点h∈Hr，即超边r同时与节点v和h关联，则存在一个正确的三元组(h，r，v)，称h是与v具有关系r的节点。当v的负样本子集为NEG(v)时，对于∀ξ∈V，节点ξ标签定义如式(7)所示。

(7)

对于给定节点序列C，平移约束目标函数定义如式(8)所示。

(8)

其中，eh+r=eh+er，θξ为ξ的参数向量。通过最大化L2，超边信息被编码到节点表示向量中。

3.5 联合优化目标函数

通过联合优化拓扑派生目标函数和平移约束目标函数来捕获节点之间的成对关系和元组关系，HRTC可以得到质量更高的节点表示向量，为了便于计算，将函数L1和L2取对数后相加并最大化联合优化目标函数如式(9)所示。

L=L1+β·L2

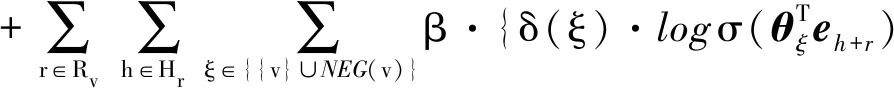
(9)

其中，β是平衡基于拓扑派生目标函数的模型和基于平移约束目标函数的模型的调和因子。为了便于推导，将最内层花括号内容简记为L(v，u，ξ，h,r)，即：

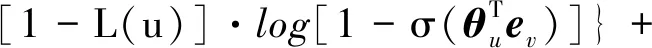
(10)

通过使用随机梯度上升(SGA)算法来优化目标函数L(v，u，ξ，h，r)，关键是给出L(v，u，ξ，h，r)的4种梯度。

首先L(v，u，ξ，h,r)关于θu的梯度计算如式(11)所示。

(11)

因此，对θu的更新如式(12)所示。

(12)

其中，α是HRTC方法的学习率。当L(u)=1和L(u)=0时，分别更新正负样本节点的参数向量。

其次，利用ev和θu的对称性来计算L(v，u，ξ，h，r)关于ev的梯度如式(13)所示。

(13)

因此，对嵌入向量ev的更新如式(14)所示。

(14)

然后，L(v，u，ξ，h，r)关于θξ的梯度计算如式(15)所示。

+[1-δ(ξ)]

·eh+r-[1-δ(ξ)]

-[1-δ(ξ)]

(15)

因此，对θξ的更新如式(16)所示。

(16)

当δ(ξ)=1或δ(ξ)=0时，分别更新正负样本节点的参数向量。

(17)

由于eh+r=eh+er，所以对eh和er的更新如式(18)、式(19)所示。

HRTC方法细节如算法3所示。

算法3 HRTC方法输入: 超网络H=(V,E),嵌入维度d;输出: 嵌入矩阵Ev∈R(|V|+|E|)×d; 1. for v in V∪E do 2. 初始化嵌入向量ev∈Rd×1 3. 初始化参数向量θv∈Rd×1 4. end for /∗C为SRwalk方法采样的语料库∗/ 5. for v in C do 6. for c in context(v) do 7. for u in {c}∪Neg(v) do 8. 根据式(12)更新θu 9. end for 10. 根据式(14)更新ev 11. end for 12. if v∈V do 13. for r in Rv do 14. for h in Hr do 15. for ξ in {v}∪NEG(v) do 16. 根据式(16)更新θξ 17. end for 18. 根据式(18)、式(19)更新eh和er 19. end for 20. end for 21. end for 22. return Ev

3.6 复杂度分析

首先，对于超图构建2-截图+关联图的过程，其时间复杂度为O(|E|·|e|2)。然后，对于感知节点语义相关性的元路径游走过程，其时间复杂度为O(N·|V1|)。最后，基于拓扑派生目标函数的模型和基于平移约束目标函数的模型共同捕获了节点之间的成对关系和元组关系过程，所需时间复杂度为O(C·(context·(Neg+1)+Rv·Hr·(NEG+1))·2d·(|V|+|E|))，其中，Neg和NEG分别表示基于拓扑派生目标函数的模型和基于平移约束目标函数的模型的负采样样本大小。因此，HRTC方法的时间复杂度为O(|E|·|e|2+N·|V1|+C·(context·(Neg+1)+Rv·Hr·(NEG+1))·2d·(|V|+|E|))。

4 实验

4.1 数据集

为了全面评估HRTC方法的效果，本节使用三个不同类型的无向超网络数据集，即一个药物网络、一个GPS网络、一个社会网络。数据集的详细统计如表1所示。

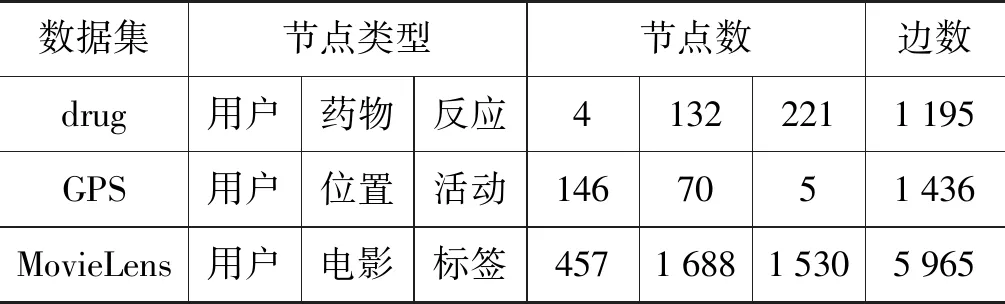
表1 数据集统计

●drug(1)http://www.fda.gov/Drugs/： 该数据集来自FDA不良事件报告系统(FAERS)。它包括提交给FDA的不良事件和用药错误报告的信息。元组关系(用户，药物，反应)被看作超边来构建超网络。

●GPS[14]： 该数据集描述了一个用户在某个位置参加活动。元组关系(用户，位置，活动)被看作超边来构建超网络。

●MovieLens[15]： 该数据集描述了来自于MovieLens 的个人标记活动。元组关系(用户，电影，标签)被看作超边来构建超网络。

4.2 基线方法

deepwalk[16]算法在随机游走节点序列上训练Skip-gram模型来获得节点表示向量。

node2vec[17]通过有偏随机游走方式，保持了网络中的高阶相似性，来学习节点表示向量。

metapath2vec[18]通过基于元路径的随机游走来构造节点的异质邻域，然后利用异质Skip-gram模型学习节点表示向量。

Hyper2vec[7]通过超边上有偏二阶随机游走来采样节点之间的高阶邻居关系，然后训练Skip-gram模型获得节点表示向量。

HPSG[8]通过基于超路径的随机游走来构造节点的异质邻域，然后通过Skip-gram模型学习节点表示向量。

HPHG[8]通过基于超路径的随机游走来构造节点的异质邻域，然后通过Hyper-gram模型学习节点表示向量。

Event2vec[19]将多个对象之间的关系建模为事件，定义了事件驱动的一阶和二阶近似性，通过学习事件嵌入来学习对象嵌入。

HRTC通过平移机制将超边融入超网络表示学习过程中。

4.3 链接预测

链接预测在现实生活中得到了广泛应用，尤其是推荐系统。本节在drug、GPS和MovieLens三个超网络数据集上进行链接预测实验。首先，使用二元算子[17]Weighted-L1和Weighted-L2计算节点成对相似性，然后，通过计算AUC[20]值来评估HRTC方法在2-截图、关联图、2-截图+关联图上的链接预测性能。

在链接预测试验中，采用80%边集作为训练集，对于所有方法分别实验10次，取AUC平均值。以drug数据集为例，HRTC方法对于2-截图、关联图，分别采用方案φ1、φ2进行采样，对于2-截图+关联图采用SRwalk方案φ3进行采样。

从表2可知，deepwalk，node2vec，metapath2vec，HRTC分别在2-截图，关联图，2-截图+关联图进行了链接预测实验，而Hyper2vec、HPSG、HPHG、Event2vec没有分解超边，直接在超图上进行链接预测实验。对于deepwalk，node2vec，metapath2vec，HRTC，2-截图+关联图均实现了优于2-截图和关联图的链接预测效果。这表明，与2-截图、关联图相比，2-截图+关联图更好地保留了超网络结构信息。与普通网络表示学习方法相比较，HRTC在3个数据集上均实现了最佳性能。与超网络表示学习方法相比较，HRTC在drug和GPS数据集上展现出了优于Hyper2vec和HPSG的链接预测能力。因为对于drug和GPS数据集，由于其超边内部节点之间不是两两语义相关的，所以特定地训练成对关系的模型Hyper2vec和HPSG没有很好地学习节点之间的元组关系。HRTC在训练节点之间的成对关系时，同时训练节点之间的元组关系，能够充分地学习节点之间的语义关系。对于MovieLens数据集，每部电影都有标签，比如喜剧、战争等。每个用户都有特定的电影类型偏好。因此，用户与电影、电影与标签、用户与标签之间都存在语义相关性，特定地学习成对相似性的方法表现较好，如Hyper2vec和HPSG与HPHG、Event2vec相比较，HRTC在MovieLens数据集上实现了优于HPHG和Event2vec的性能，在drug和GPS数据集上实现了与HPHG竞争性的效果。以上分析表明了HRTC可以很好地保留超网络节点之间的语义关系，而且HRTC更加适用于超边内部节点之间具有语义相关性的超网络。

4.4 超网络重建

超网络重建是评估节点表示向量质量的典型方法。本节在drug和GPS数据集上评估了HRTC在不同重建比率下的性能。超网络重建[7]的评估指标定义如式(20)所示。

表2 链接预测结果 (单位： %)

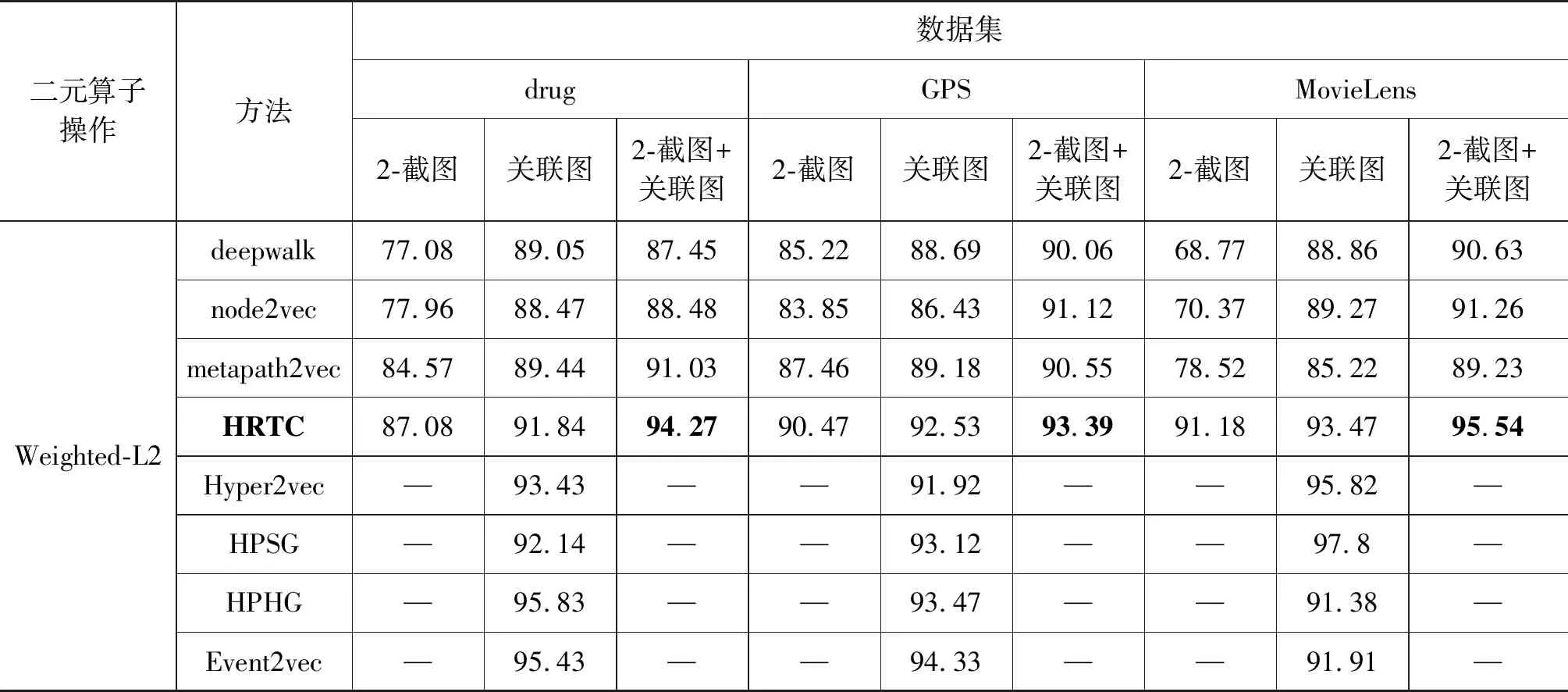
续表

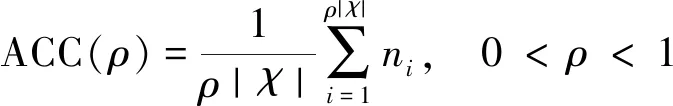
(20)

其中，对重建超边的元组相似性按照升序排序，ni=1表示第i个重建超边存在于原超网络中，否则ni=0。|χ|为重建的总超边数，ρ为超边重建比率。

超网络重建结果如图8所示，在两个数据集上，HRTC在2-截图+关联图上的效果均好于2-截图和关联图，表明了团扩展和星型扩展结合的优越性。此外，HRTC在两个数据集上的重建效果显著地优于普通网络表示学习方法。在两个数据集上，其他超网络表示学习方法在重建小比率超边时表现不错，在增大重建比率时，其效果下降明显，而HRTC在各个比率的超边重建任务中都展现出了优越的性能，而且HRTC在GPS数据集上显著优于其他基线方法。这表明HRTC通过捕获节点之间的元组关系获得了质量较高的节点表示向量。

图8 超网络重建

4.5 参数敏感度分析

HRTC方法具有超参数β，它是一个平衡基于拓扑派生目标函数的模型和基于平移约束目标函数的模型的调和因子，选取最优的β值可以获得高质量的节点表示向量。当β=0时，HRTC只能捕获节点之间的成对关系，当0<β≤1时，HRTC可以同时捕获节点之间的成对关系和元组关系。为了综合考虑上述情况，设置0≤β≤1。ρ表示超边重建比率，ρ=0.1表示重建10%的超边，ρ=1表示重建全部的超边。设置0.1≤ρ≤1，取各个超边重建比率的平均值使得实验分析更具有普遍性。具体来说，通过在drug和GPS数据集上的链接预测和超网络重建任务分析参数β的影响。其中，ACC(L)为链接预测Weighted-L1和Weighted-L2的平均值，ACC(ρ)为超网络重建值的平均值。

由图9可知，对于drug和GPS数据集，当β=0时，HRTC方法仅捕获了节点之间的成对关系，没有考虑节点之间的元组关系；当0<β≤0.6和0<β≤0.8时，链接预测和超网络重建性能随着β的增大而增大，并且分别在β=0.6和β=0.8时达到最大，说明元组关系的重要性在增强，成对关系的重要性在降低；当0.6<β≤1和0.8<β≤1时，链接预测和超网络重建性能随着β增大而减小，说明元组关系的重要性在降低，成对关系的重要性在增强。出现上述结果的原因是节点表示向量的质量取决于成对关系和元组关系之间的平衡优化，即，通过随机梯度上升算法使得式(9)联合优化目标函数达到最优解。总之，节点之间的成对关系和元组关系对于超网络表示学习都很重要。

图9 参数敏感度分析

5 结束语

为了进行超网络表示学习研究，本文首先提出一种结合团扩展和星型扩展的方法将超网络转换为异质网络，其次，提出感知节点语义相关性的元路径游走方法来保留节点之间的成对关系和元组关系。再次，通过引入平移机制，提出基于平移约束的异质超网络表示学习方法来捕获节点之间的成对关系和元组关系，最后，在三个不同类型的超网络数据集上进行了评估实验。实验结果表明，HRTC方法可以很好地发现那些未知链接，并以较好的效果重建超网络。尽管该方法通过超图到图的转换策略开展了超网络表示学习研究，并尝试在表示学习过程中融入超边信息，但是仍然会丢失一部分超网络结构信息。因此，将来的研究可以从两个方面展开，一是继续尝试在网络表示学习方法中融入超边信息；二是不再将超网络转化为普通网络，即不再分解超边，而是将超边看成一个整体，进行超网络表示学习研究。