钙质砂粘性土的渗透特性

朱学敏， 代佳骏， 马 露， 肖昕迪

(安徽科技学院 建筑学院， 安徽 蚌埠 233000)

我国钙质砂主要分布在南沙群岛至山东沿海。自20世纪70年代以来，近海工程迅速发展，此类工程面临的最大难题是沿海地区土质较为复杂，地下水影响较大，特别是含钙质砂的粘性土。钙质砂颗粒内部空隙较多，形状不规则且易破碎，主要组成是碳酸盐，其中CaCO3占比超过90%，并夹杂有珊瑚、藻类、贝壳等海洋生物[1-2]。

1856年,法国工程师Darcy提出均质砂土在层流情况下流速v与渗透系数k和水力坡降i的关系公式为v=ki[3]；随着研究的继续深入，相继有Terzaghi等[4-6]探究了各种不同因素对渗透系数的影响规律，并在试验基础上提出了渗透系数的计算公式；苏立君等[7]研究了渗透系数随孔隙率和颗粒粒径的变化规律，提出了渗透系数的计算公式，发现该经验公式具有较高可靠性，但缺乏针对粘性土渗透特性的研究；廖仁国等[8]分析了钙质砂和石英砂在不同围压下的渗透规律和变形规律，但对于渗透系数的理论计算公式未作出相应研究；钱琨等[9]研究了钙质砂颗粒级配和孔隙比与渗透系数的关系，得到渗透系数计算公式，但该计算公式仅能反映钙质砂的渗透特性，对于混合土层渗透系数计算的适用性有待进一步研究；胡明鉴等[10]考虑细颗粒含量对钙质砂地层渗透特性的影响，发现细颗粒存在最佳含量，最佳含量细颗粒下渗透系数的变化最为显著。

本文在试验数据分析的基础上提出一种经验公式，旨在提出一种简便方法计算渗透系数以运用于实际工程中。

1 试验材料及试验过程

1.1 试验材料

土样材料有高岭土和钙质砂，高岭土是一种以高岭石族粘土矿物为主的粘土和粘土岩，钙质砂来源于南海某地区，初始钙质砂原材料含有丰富的内空隙如图1所示，钙质砂原材料经破碎筛分后即可得试验所用材料。将钙质砂与高岭土按不同比例混合后得到颗粒累计级配曲线如图2所示。通过颗粒级配累计曲线可求得不同钙质砂含量下土体不均匀系数与曲率系数如表1所示。根据图分别取各组试样的有效粒径d10、平均粒径d30、限制粒径d60，计算不均匀系数Cu和曲率系数Cc：

(1)

(2)

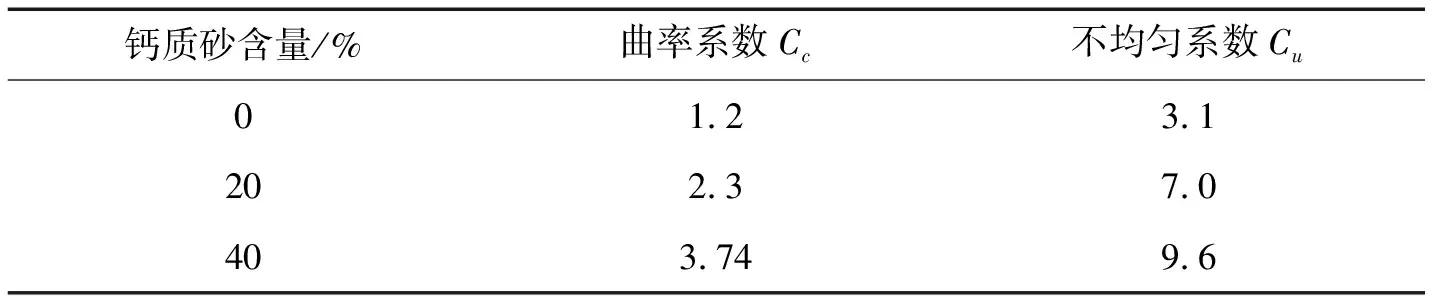
表1 不同钙质砂含量下曲率系数与不均匀系数

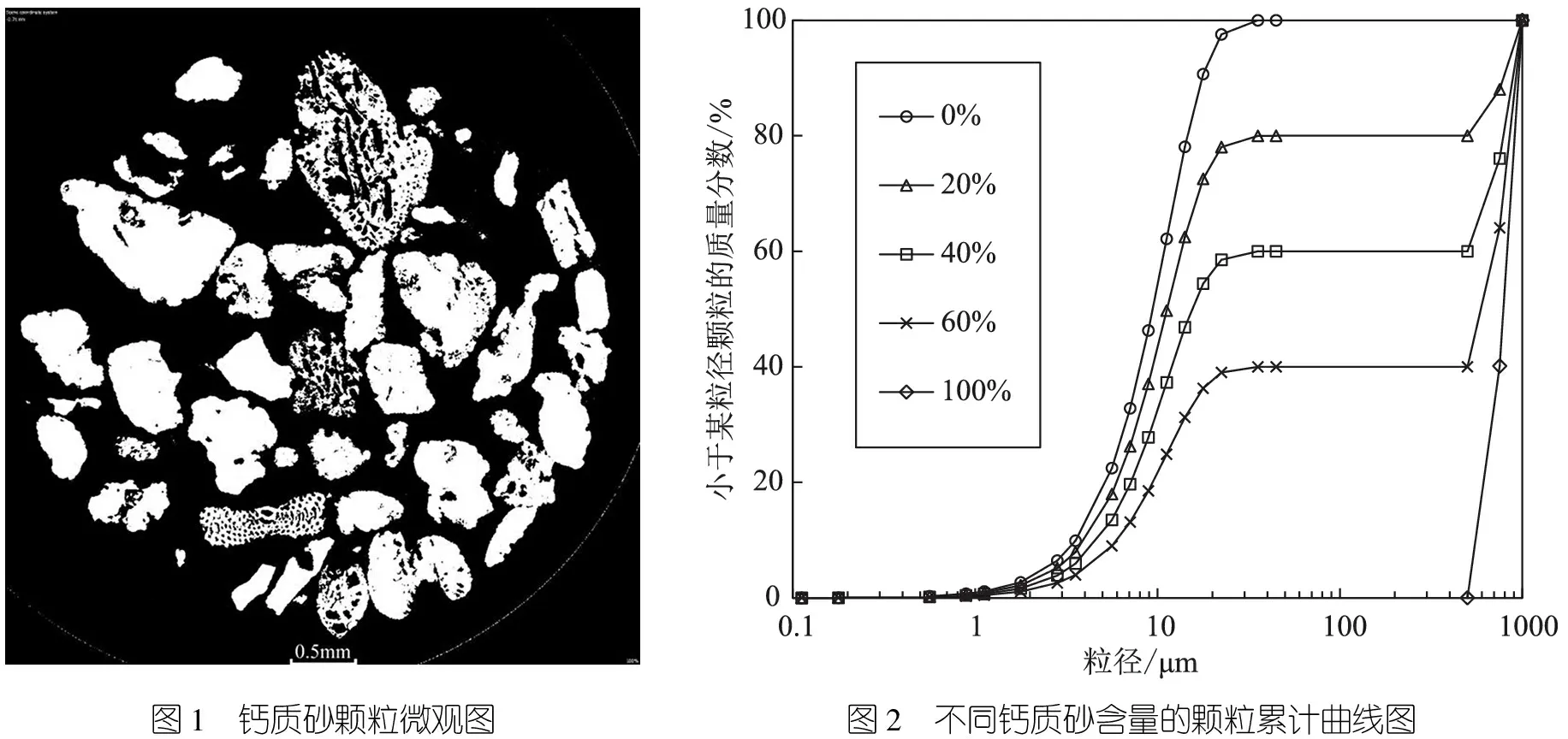
图1 钙质砂颗粒微观图图2 不同钙质砂含量的颗粒累计曲线图

1.2 试验过程

高岭土属于粘性土，渗透性能较差，采用变水头试验。变水头渗透容器内径为100 mm，筒高400 mm。环刀内径为61.8 mm，环刀高度为40 mm。试验步骤按照《土工试验规程》中的具体方法进行操作，在制样前将环刀内壁均匀涂抹适量凡士林，避免环刀内壁渗水确保试验数据的精确度；为了保证制样的完整性且试验能填充满环刀，根据不同孔隙比选择合适含水量制配试样，再根据不同孔隙比和不同钙质砂含量分别进行制样，每个试样分5层进行装填，各层土样质量相等并以相同击实功击实，以确保试样的均匀性。在进行渗透试验前，将试样放入真空缸内抽气进行饱和以提高试验精度，抽真空时间持续约1 h；试样饱和后，将装有试样的环刀装入渗透仪中，先将进水阀打开出水阀关闭，再压水进入标有刻度的渗流管中，水柱达到合适高度后关闭进水阀打开出水阀，为防止过大水头破坏试样，取水头为15 cm进行渗透试验；待渗透仪软管中有水流出开始记录数据，同时使用秒表计时，测出水柱下降15 cm所需时间，重复上述步骤2次。计算渗透系数

(3)

式中：a表示变水头管的截面积；L为试样高度；A为试样截面积；t1、t2分别为测读水头的起始时间和终止时间；H1、H2为起始和终止水头。为提高精确度，每个试样的渗透系数取3次重复试验结果的平均数。

2 试验结果分析

2.1 孔隙比对渗透系数的影响

将不同钙质砂含量的土样分别压实到不同孔隙比，并在直角坐标系中绘制渗透系数与孔隙比的关系曲线，来描述随着孔隙比的增加渗透系数的变化规律。对不同钙质砂含量的土样所得试验结果进行线性回归分析，并通过散点图和趋势线研究孔隙比e与渗透系数k之间的相关性。对数据进行分析处理，得到的结果如图3所示，不同钙质砂含量的土样渗透系数k与10e(e为孔隙比)的线性相关度为R2。

从图3可以得出在钙质砂含量为0%时，随着孔隙比的逐渐增大，渗透系数也随之增大，渗透系数k与10e的一次方呈现正相关关系，且两者的线性相关程度较高，渗透系数k与10e的拟合公式可以表示为：

k= (0.131 5×10e- 0.438 6)×10-4

(4)

拟合得到的相关系数R2=0.982 9。在钙质砂含量为20%和40%时也具有相同的规律。以微观角度来研究，在钙质砂含量确定的前提下，颗粒级配的影响可以忽略，在孔隙比逐渐增大的情况下，单位体积土样内孔隙所占比率也随之增加，孔隙的平均直径也相应增大，土样内部的渗流通道也对应变宽，在压力水头一定时，水流受到的阻力变小，单位时间内的渗流量增加，体现在宏观上的现象为渗流管中的水柱下降速度变快。

2.2 钙质砂含量对渗透系数的影响

将不同钙质砂含量的土样击实到同一孔隙比下进行渗透试验，将所得到的结果绘制于直角坐标系中，进行相关性研究，所得结果如图4所示。从图4可以看出，在相同钙质砂含量下不同孔隙比对应的渗透系数也有所不同，渗透系数随着钙质砂含量的增加而有所增加，40%钙质砂含量试样的渗透系数约为纯高岭土试样的2.5倍。由图可知渗透系数k与10s(s为钙质砂含量)具有良好的线性正相关性，孔隙比为0.8、0.95和1时对应的相关性系数分别为0.935 1、0.999 7和0.996 4，由此可知钙质砂含量与渗透系数的相关程度极高。在土样孔隙比相同的前提下，土体内部孔隙体积相等，而钙质砂相比于高岭土其颗粒较大，颗粒表面粗糙、棱角多、透水性好，在钙质砂含量逐渐增大的情况下，土颗粒之间尺寸增大，孔隙的平均直径也相应增大，土样内部容易形成渗流通道；而在孔隙体积不变的情况下，孔隙平均直径增大，孔隙数量减少，因此水流流过的路径变短，水流通过土样的速度变快。

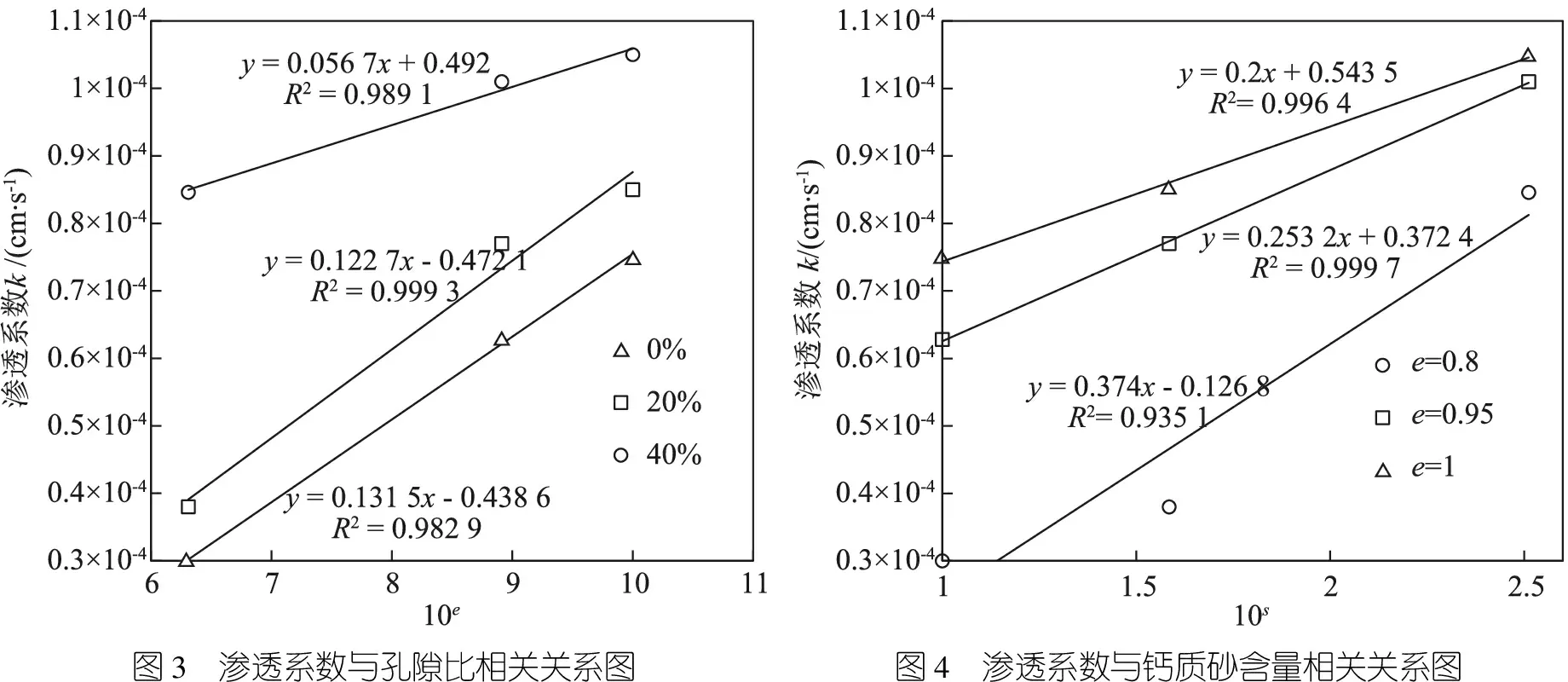
图3 渗透系数与孔隙比相关关系图图4 渗透系数与钙质砂含量相关关系图

2.3 不均匀系数对渗透系数的影响

在土样孔隙比一定的的前提下，将不均匀系数与渗透系数的关系绘制于直角坐标系中，所得结果如图5所示。由图可知，随着不均匀系数的逐渐增大，土样的渗透系数也相应增大，并且两者之间存在较好的线性相关性，孔隙比为0.8、0.95和1时，渗透系数与不均匀系数的线性相关系数分别为0.757 7、0.926 7和0.902 7。不均匀系数是反映土体颗粒均匀程度的一个指标，不均匀系数一般大于1，越接近1表示土体越均匀，级配不良；不均匀系数越大表示土体中颗粒粒径的涵盖范围越大。在不均匀系数较大的情况下，颗粒粒径的大小差异很大，较粗颗粒之间存在的孔隙需要细颗粒填充，而在孔隙比一定时，不均匀系数越大粗颗粒之间的孔隙不足以完全被细颗粒填充，导致没被填充的孔隙越多，更容易形成渗流通道致使渗透系数变大。孔隙比为0.8时，渗透系数与不均匀系数的相关程度相比其他两种孔隙比工况有较大降低，造成此现象的原因可能是掺入钙质砂后缺少某些粒径的颗粒，使不均匀系数变化较大不能准确地反映不均匀系数对渗透系数的影响。

2.4 曲率系数对渗透系数的影响

在保持土样孔隙比不变的前提下，将曲率系数与渗透系数的关系表示于直角坐标系中，所得结果如图6所示。由图可知，随着曲率系数的逐渐增大，土样的渗透系数也相应增大，并且两者之间存在极高的线性相关性，孔隙比为0.8、0.95和1时，渗透系数与曲率系数的线性相关度分别为0.852 6、0.976 6和0.961 8。曲率系数是反映土体颗粒粒径连续性的一个指标，曲率系数大于1小于3表示土粒相的粒径齐全，连续分布。曲率系数越大，表示平均粒径d30与有效粒径d10之间的差异越大，甚至可能会缺少某些粒径的颗粒，在颗粒累计级配曲线中出现水平段。随着曲率系数的增大土样不连续性程度增加，某些粒径颗粒的缺失使得粗颗粒之间的孔隙不足以被细颗粒完全填充，导致没被填充的孔隙增多，形成渗流通道致使渗透系数变大。

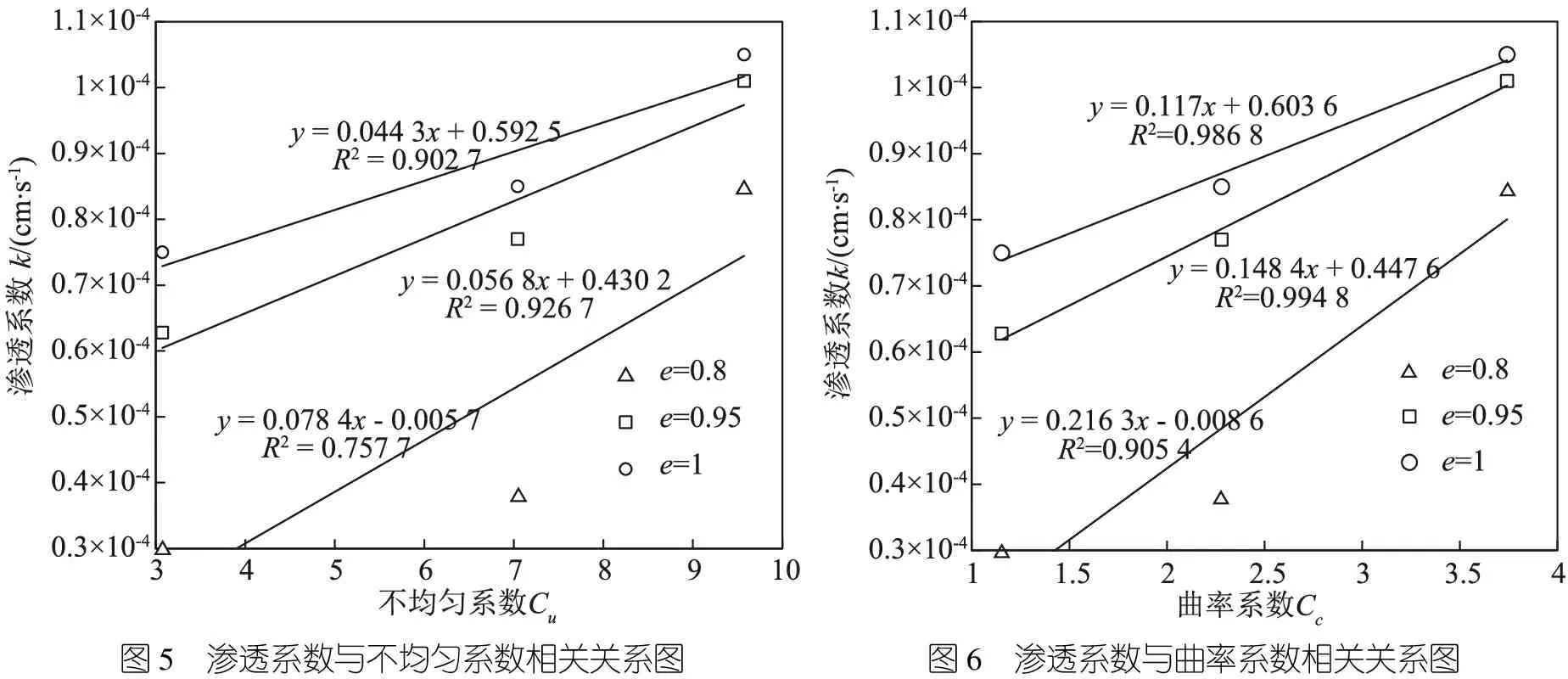
图5 渗透系数与不均匀系数相关关系图图6 渗透系数与曲率系数相关关系图

3 渗透系数计算公式

通过对试验数据整合、制图及分析可以得到试验土样的渗透系数与10e(e为孔隙比)、钙质砂含量s、不均匀系数Cu和曲率系数Cc有较强的相关性。在分析影响土样渗透系数因素的过程中采用因素分析法进行研究，该方法通过改变某一要素的值而保持其他要素不变,通过分析渗透系数与单一因素的线性相关性得出相应的拟合公式，通过图表可以得出每个因素与渗透系数呈现较好的正相关关系。为了将各个影响因素都能反映在一个公式中，可以把上述参数相乘并进行修正，建立经验公式以表述土样渗透系数的大小，以便将所得公式应用于实际工程实践中，经验公式如下：

k=B·10s10eCuCc×10-8

(4)

式中：k为渗透系数，cm/s；B无量纲。将试验所得数据代入建立的经验公式，反复验算以推算出B的值。通过反演计算，可以得出当B取14时渗透系数计算值与试验所得实际值之间差异较小，因此取B=14。

为了验证经验公式的可靠性，将本文经验公式计算值k、太沙基公式计算值kT、哈增公式计算值kH、苏立君公式计算值k苏、朱崇辉公式计算值k朱与通过试验测得渗透系数的实测值的比值列于表中，渗透系数经验公式计算值与实测值的对比如表2所示。经过对比分析发现，对提出的4种影响因素进行修正拟合得到的渗透系数计算公式相比于太沙基公式、哈增公式等提高了精确度，经验公式计算值与实测值的比值在0.90～1.25之间，具有为实际工程提供参考的价值，特别是对于含有钙质砂的软黏土工程，一定程度上解决了计算其渗透系数的难题，实用性较高。由表2可知各种渗透公式计算所得结果差异明显，原因在于各种方法研究的对象和工况不同，其他研究者大多研究单一颗粒组成时的渗透系数影响因素，但实际情况下土体组成多样，内部结构极为复杂，即使土体内部有细微变化，对渗透系数的影响也极其明显，因此如何利用有效的方法和合适的颗粒组成模拟实际工程中复杂多变的工程状况是后续研究的重点。本文的土样特殊，是存在于富含钙质砂和软弱黏土的南海地区，提出的经验公式为该地区土体渗透特性研究提供理论支持。

表2 渗透系数经验公式计算值与实测值的对比表

4 结 语

在钙质砂含量一致的前提下，土样的渗透系数随孔隙比的增加而相应增加，并且渗透系数与10e之间存在密切的正相关性关系。对于孔隙比相同的土样，土样的渗透系数随钙质砂含量的增加而显著增加，相比于孔隙比的影响程度，钙质砂含量的变化对渗透系数的影响更加突出，并且渗透系数与10s有较好的线性相关性。在孔隙比保持不变的情况下，不均匀系数与曲率系数的变化都会影响土样的渗透系数，并且渗透系数与两者均存在好的线性相关性。先分析孔隙比、钙质砂含量、不均匀系数和曲率系数对土样渗透系数的影响，再综合考虑4个因素的共同作用，并提出渗透系数的经验计算公式，精确度较高，在实际工程中具有一定的参考价值。