不等式约束最优化问题最优性条件的教学

孙敏，田茂英

（1.枣庄学院 数学与统计学院，山东 枣庄 277160；2.山东煤炭卫生学校 生理学教研室，山东 枣庄 277160）

最优性条件是最优化方法课程的教学重点.一方面，最优性条件给出了最优解满足的必要条件，因此，通过求解最优性条件可以得到可能的最优解，从而将搜索范围从可行域缩小到有限个稳定点或KKT点；另一方面，最优性条件在最优化问题的算法设计中起着关键作用.实际上，很多最优化算法的迭代格式、终止条件等的设计动机来自于最优性条件[1-5]，如增广拉格朗日乘子法中乘子迭代格式的设计，可分裂凸规划的交替方向法对偶变量迭代格式的设计等.最优性条件在很多领域有着广泛的应用，是很多机器学习问题分析的必要方法[6-7].

最优性条件是最优化方法课程的教学难点.在学习高等数学多元函数约束极值问题时，通过引入拉格朗日函数，将含等式约束的优化问题转化成无约束优化问题，进而借助无约束优化问题的最优性条件给出了等式约束最优化问题的最优性必要条件.但是由于不等式约束优化问题最优性条件的证明需要引入更多的符号与概念，因此国内常用的高等数学教材一般不对该问题进行研究.一般的最优化教材往往按照下面的思路研究该问题：为了给出不等式约束最优化问题的最优性条件，首先，引入3类向量集合，即可行方向集合、线性化锥和下降方向集合；然后，给出前2个集合的等价条件，后2个交集是空集的等价代数形式，该等价形式即为最优化问题的最优性一阶必要条件.由于线性化锥与下降方向集合的交集可以表示成一个线性系统，因此通过Farkas 引理，该交集是空集等价于一个对应的线性系统有解，而由线性系统有解可得到最优性条件的代数形式[8-10].

具体分析过程见图1.

图1 不等式约束最优化问题的最优性条件

考虑一个简单的实例来说明不等式约束最优化问题的最优性条件分析过程.

例1考虑不等式约束优化问题

分析类似于数学分析课程所学的分析方法，为了求解该问题的最优解，需要找出可能的最优解，即挖掘最优解应该具有的性质.显然，最优解应该满足：（1）可行性；（2）在最优解处，沿着任意方向前进任意小的步长后，要么出了可行域，要么目标值上升，这说明在该点处不存在一个方向既是可行方向又是下降方向.由此分析得到最优解应该满足条件

式中：I（x1,x2）为有效约束集合.于是必要条件可以松弛为

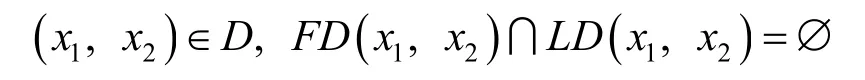
这样处理产生了2个问题：（1）在什么条件下，FD（x1,x2）=LD（x1,x2）；（2）LD（x1,x2）的定义是一种隐式的形式，即只有知道了（x1,x2），才能求出I（x1,x2），这样才能将LD（x1,x2）表示成不等式组.我们的目的就是求（x1,x2），这与求二次规划的积极集时遇到的问题一样，因此需要引入Farkas 引理，给出一个线性系统无解与另一个线性系统有界的结论，进而导出约束优化问题的一阶必要条件.

由分析过程可以看出，与无约束最优化问题或等式约束最优化问题的最优性条件不同，不等式约束最优化问题的最优性条件需要引入集合、线性系统、Farkas 引理等一系列新的概念或结论.与同样类型的问题相比，其分析过程有些繁琐，没有充分利用已经得到的结论.

课程教学内容的起承转合对于学生建构一门课的内容体系起着非常重要的作用.本文针对不等式约束最优化问题的最优性条件设计一套全新的教学过程，其充分利用了等式约束最优化问题的最优性条件，避免了集合、线性系统、Farkas 引理等元素，遵循了“如无必要，勿增实体”的奥卡姆剃刀原理.

1 等式约束最优化问题的最优性条件

回顾等式约束最优化问题的最优性条件.考虑等式约束最优化问题

2 不等式约束最优化问题最优性条件的教学设计

基于等式约束最优化问题的最优性条件，给出不等式约束最优化问题最优性条件的教学设计.为了讨论过程的简洁，考虑只含不等式约束的最优化问题

2.1 问题（1）与问题（2）的区别

问题（2）与问题（1）的区别只在于将等式约束换成了不等式约束.回顾在化线性规划的一般形式为标准形式时，通过引入松弛变量可以将不等式约束转化成等式约束.如对于约束x1+2x2≤ 1，引入松弛变量x3，得

为了保持约束的线性性，要求松弛变量x3非负.

2.2 形式转化

受线性规划标准化（3）的启发，通过引入松弛变量，将问题（2）转化成问题（1）的形式，即

2.3 初步结果

根据定理1 可得到问题（4）最优解满足的一阶必要条件.为此引入向量ei∊Rm表示单位向量，其第i个元素为1，其余元素全为0.

2.4 乘子非负性的讨论

与KKT 条件相比，式（7）对乘子的符号没有施加限制，需要再考虑二阶必要条件.

2.5 线性无关的讨论

例2直接利用等式约束优化问题的最优性条件求解例1 中的不等式约束优化问题.

解引入松弛变量y1,y2，得

利用等式约束优化问题的必要条件得

取d=（0,0,λ1,0），则d显然满足 2d1x1+d2+2d3y1=0,d1+2d2x2+2d4y2=0，于是由等式约束的二阶必要条件可知，2λ13≥0，即λ1≥0.类似地，取d=（0,0,0,λ2），可得λ2≥0.将这些条件综合到一起就得到了约束优化问题的K-T 条件.进而利用该K-T 条件求出可能的极值点，再结合最优性的二阶必要与充分条件可以得到该问题的最优解.

比较例1 与例2 可以看出，直接利用等式约束优化问题的最优性条件来推导不等式约束优化问题的最优性条件是可行的，并且更便于学生理解这个知识点，同时便于构建起这一部分的知识逻辑体系.

3 结语

最优性条件是最优化方法课程的基础而重要的内容.基于等式约束最优化问题的最优性条件，本文给出了不等式约束最优化问题一阶最优性必要条件的一种新的教学设计思路.该思路没有用到Farkas 引理，整个教学设计与已经学过的知识紧密结合，可以使学生从整体上更好地理解与掌握相关知识点，进而建构起最优化方法的结构体系.今后，将基于等式约束最优化问题的二阶条件给出不等式约束最优化问题二阶条件的教学设计.