四川盆地威远区块页岩气单井产量预测方法及应用
韩 珊,车明光,2,苏 旺,肖毓祥,吴忠宝,陈建阳,汪莉彬
(1.中国石油勘探开发研究院,北京 100083;2.中国科学技术大学,安徽 合肥 230027)
0 引 言
近年来,得益于理论的创新突破与技术的快速进步,中国页岩气勘探开发取得了跨越式发展。为了准确计算页岩气单井可采储量,科学开展页岩气井产能规划和投资决策,明确影响页岩气产量的主控因素及优选适用于页岩气产量预测方法显得尤为重要。页岩气藏资源潜力巨大[1],产能评价较为复杂。常规的页岩气产量预测方法主要为数值模拟方法和公式推导法,2种方法可对单井可采储量(EUR)及日产量进行预测。庞进等[2]通过流态划分得到不同地层流动阶段的预测产量,认为复合线性流之后预测效果最好。刘传斌等[3]利用数值模拟方法对SEPD模型、Duong模型和YM-SEPD模型进行分析,认为组合模型预测日产量精度更高。李海涛等[4]提出基于裂缝流主导的产量递减预测新方法预测EUR。然而,前人对于页岩气单井首年累计产量的预测研究较少。
近年来,机器学习方法已经应用于石油工业中的多个领域,并初步取得了良好效果。位云生等[5]、彭成勇等[6]利用机器学习方法开展了压裂选井评层研究。孙东生等[7]、马志国等[8]利用人工神经网络法对水力压裂效果进行了评价。严禛等[9]将机器学习方法应用于油田产量预测工作中。机器学习方法可以实现在有限数据量的条件下对复杂问题进行建模、优化及预测。
目前,四川盆地威远区块页岩气勘探开发正处于大规模发展阶段,其优越的地质条件为页岩气赋存与富集提供了良好的条件。以四川盆地威远区块页岩气田为研究对象,基于132口投产1 a以上气井的地质与工程数据及动态生产数据,采用灰色关联法研究影响产量的主控因素,在此基础上使用支持向量机与BP神经网络方法预测该气田单井首年累计产量及初期产量,并对上述方法进行对比及应用效果分析,进而优选出适用于页岩气产量预测的机器学习方法。对单井首年累计产量及初期产量进行预测,可为新开采井进一步预测单井EUR工作提供更准确的基础数据,进而可有效地调整现场开发方案,对页岩气田的产能规划和快速开发起到积极作用,对页岩气田的后续开发具有指导性意义。
1 原理与方法
1.1 支持向量机法
支持向量机(Support Vector Machine,SVM)是机器学习方法中的一种,最早由数学家Vapnik提出。支持向量机可以实现分类和回归2种功能,此次研究使用支持向量机回归法(SVR)对页岩气井首年累计产量进行预测。支持向量机在样本数量较少的情况下能够保证一定的预测精度,在压裂效果预测及增油量预测中可发挥一定的优势[10]。对于线性问题,首先使用线性回归函数,将给定样本数据进行拟合。
f(x)=wx+b
(1)
式中:w为斜率;b为截距;x为样本数据;f(x)为样本数据的拟合函数。
式(2)为支持向量机回归的目标函数,其可以提高模型的泛化能力,避免出现过度拟合的问题。式(3)用于减少模型误差[11]。
(2)
(3)
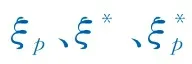
引入拉格朗日乘子以及对偶变量对模型进行优化,将式(2)、(3)转化为式(4)、(5)。
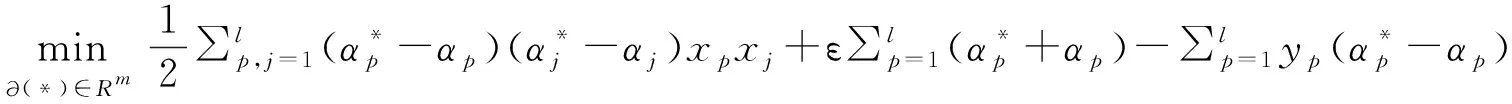
(4)
(5)
由于该研究的气井产量预测问题为非线性问题,需通过核函数将样本数据映射到高维空间中进行线性回归。为此,引入RBF(Radial Basis Function)核函数,通过调整RBF核函数参数以适用于所用样本集[12]。
k(x,xp)=exp(-g‖x-xp‖2)
(6)
式中:k(x,xp)为核函数;g为超参数。
1.2 BP神经网络
BP(Back Propagation)神经网络为机器学习方法中应用较为广泛的方法,其可以处理大量的非线性数据,通过模拟大脑神经网络处理信息的方式,将输入的样本数据进行数据处理、训练学习。在页岩气田单井首年累计产量预测工作中,BP神经网络法可仅通过输入静态数据,得到误差较小、精度较高的预测结果,适用于压裂后产气量预测工作[13]。BP神经网络主要为3层前馈网络,包括输入层、隐含层及输出层。该方法的核心是“误差反向传播”学习算法,即当正向传播中样本输出结果与预期不同时,转为反向传播进行学习。神经网络的学习过程为2个传播过程周期循环[14]。神经元输出值的计算公式为。
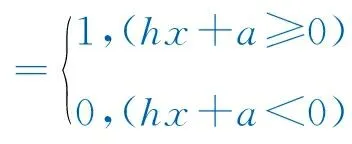
(7)
式中:h为连接神经元的权重值;a为基础值。
(8)

建立BP神经网络模型,并利用式(9)计算误差E。当误差足够小或达到迭代步数时,停止该算法计算[15]。
(9)
(10)
式中:E为误差;Ep为中间误差;L为迭代步数;di为期望输出值;zi为实际输出值。
2 数据预处理与模型建立
四川盆地威远区块页岩气田地质条件优越,资源丰富,储层连续性好且相对稳定,开发潜力大。以威远区块132口投产1 a以上气井的地质、工程及生产数据作为样本数据,建立单井产气量预测模型;采用该区块投产首年气井累计产量及初期产量为目标属性分别开展模型预测工作。
前期研究表明,影响页岩气产量的因素众多,包括地质、工程等多方面因素。通过系统梳理,统计了该气田132口气井的基础数据,包括水平井垂深的中值(m)、孔隙度(%)、总有机碳含量(%)、压力系数、水平段长度(m)、压裂段长度(m)、压裂改造段数、平均簇间距(m)、压裂液量(m3)、支撑剂量(m3)、石英砂用量(t)、平均砂比(%)、施工排量(m3/min)、平均段长(m)、加砂强度(t/m)、用液强度(m3/段),共计16项参数。其中,压裂液均为滑溜水,支撑剂均为70/140目石英砂和40/70目陶粒。上述影响因素之间存在着一定的相关性,单个因素的改变会对其他因素产生不同程度的正相关或负相关影响。因此,通过单因素拟合分析来预测产气量的方法并不准确可靠,局限性较大。在预测产量时,需要综合考虑多因素的复杂情况,而机器学习方法能够更好地将问题简单化,从而快速准确地预测目标属性。
2.1 主控因素分析
为了明确影响页岩气单井产量的主控因素,采用灰色关联法[16]对上述16个因素按影响气井产量的强弱程度排序。灰色关联评价方法的主要步骤如下。
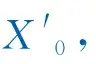
(11)
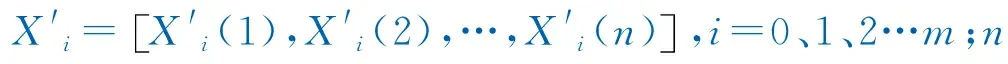
(2) 对序列进行无量纲化处理。使用初始值方法,将整个序列值除以序列中的第一个值,得到新的序列。
新形成的序列为:
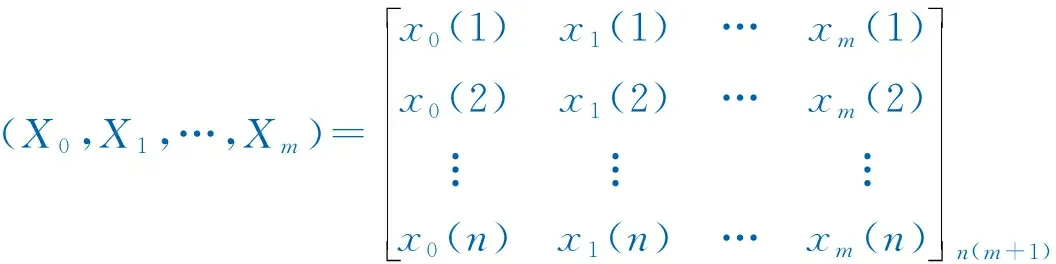
(12)
式中:Xi=[X1(1),X2(2),X3(3),…,Xi(n)],i=0、1、2…m。
运用式(12)对初始值进行无量纲化:
(13)
式中:k*=1,2,…,n。
(3) 对序列进行求差。将矩阵(12)中的第一列与其他各列求取对应的绝对差列,形成绝对差值矩阵:
矩阵中的最大值(MAX)和最小值(MIN)即为最大差和最小差。
Δ0i(k*)=|x0(k*)-xi(k*)|
(14)
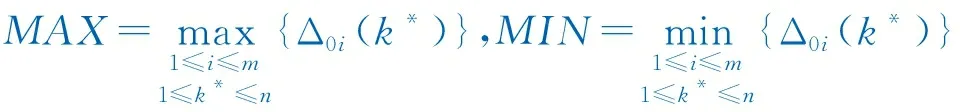
(15)
(4) 计算关联系数。将矩阵(14)中的数据用式(16)进行变换,得到如下矩阵。
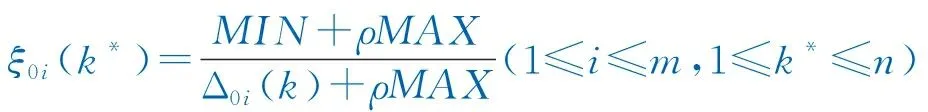
(16)

式中:ξ0i(k*)为关联系数。
分辨系数ρ在(0,1)内取值,ρ值越小,表明各系数之间的差异越大。关联系数ξ0i(k*)是不超过1的正数,Δ0i(k*)值越小,ξ0i(k*)值越大。当Δ0i(k*)=0时,ξ0i(k*)=1,这说明第i个比较序列Xi与参考序列X0在第k*期值相同。
(5) 关联度计算。由于得出的每个关联系数所反映的信息比较分散,将n个关联系数取平均值即可得到关联度,可以反映各因素对于因变量的影响程度。
(17)
式中:r0i为关联度。
(6) 关联度排序。对各比较序列与参考序列的关联度进行从大到小的排序,当关联度越大时,说明比较序列和参考序列的变化趋势越趋于一致。通过关联度可以判断比较序列和参考序列的曲线相似度。当2个序列曲线趋势越接近时,表示两者关联度越大;反之,则关联度越小。
通过上述方法,得到关联程度排序前8位的影响气井产量的主控因素(表1),即支撑剂量、压裂改造段数、水平井垂深的中值、压裂段长度、压裂液量、孔隙度、压力系数、加砂强度。
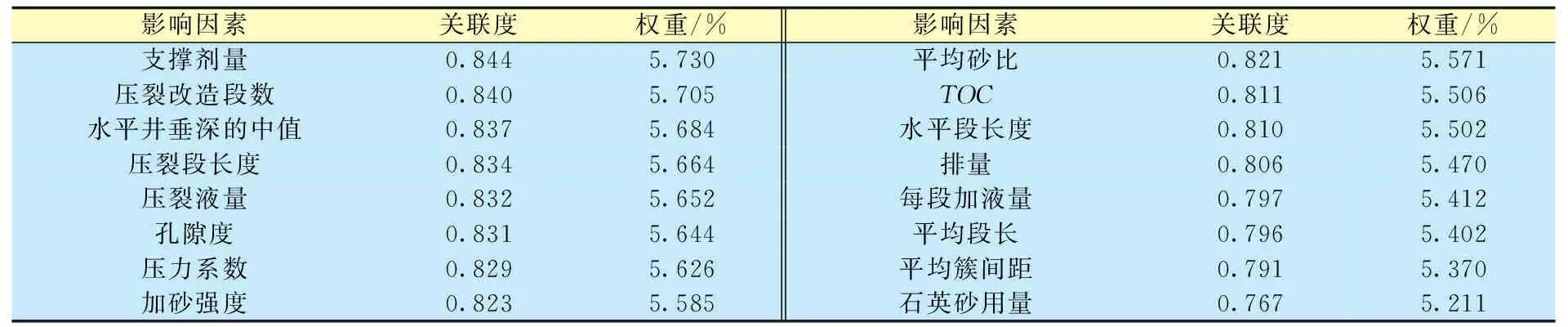
表1 影响气井产量的各因素关联度及权重大小Table 1 The correlation degree and weight of factors affecting gas well production
2.2 构建样本集
基于灰色关联法分析所得出的影响产量的主控因素,设定Xi为目标区块气井的特征向量。目标属性为预测气井生产首年的累计产量。选取目标区块132口井基础数据作为样本数据集。抽取一定的样本数据作为训练集,剩余样本数据作为测试集。
2.3 评价指标
为了评价模型的稳定性及预测精度,采用线性回归决定系数(R2)和均方误差(mse)这2个评价指标。线性回归决定系数表示拟合优度,能够反映训练集拟合结果的好坏。
R2=SSR/SST=1-SSE/SST
(18)
SST=SSR+SSE
(19)
式中:SST为总平方和;SSR为回归平方和;SSE为残差平方和。
mse表示参数预测值与真实值之差平方的期望值,其值越小,越表明模型具有更好的精确度。
(20)
2.4 模型建立
使用MATLAB软件实现算法。首先导入样本数据集,将训练集数量初始值设定为100,测试集数量为32,通过学习训练在样本数据集中随机产生训练集和测试集。创建支持向量机(SVM)预测模型,将SVM类型设置为e-SVR,其中,损失函数p值设为0.1,核函数类型设置为RBF核函数。
创建BP神经网络模型,将学习速率设定为0.1,训练的最大次数定为1 000,显示中间结果周期设定为10,全局最小误差定为0.000 1。
分别对上述2个模型的训练集进行学习训练,模型训练结束后对测试集进行验证,返回均方误差和线性回归决定系数2个评价参数值。不同的训练集数量会对模型预测精度产生一定的影响,因此,需要对训练集数量不断调整,将训练集数量从100逐一递增至122进行模型训练,将返回的mse与R2值进行统计分析比较,具体结果如图1所示。
由图1可知:支持向量机模型的大部分R2数据点在BP神经网络模型之上,表明支持向量机训练拟合程度要更高、更稳定。在训练样本数量为117时,支持向量机模型的线性回归决定系数达到最高点,R2最大值为0.951;在训练样本数量为113时,BP神经网络模型的线性回归决定系数达到最高点,R2最大值为0.912。
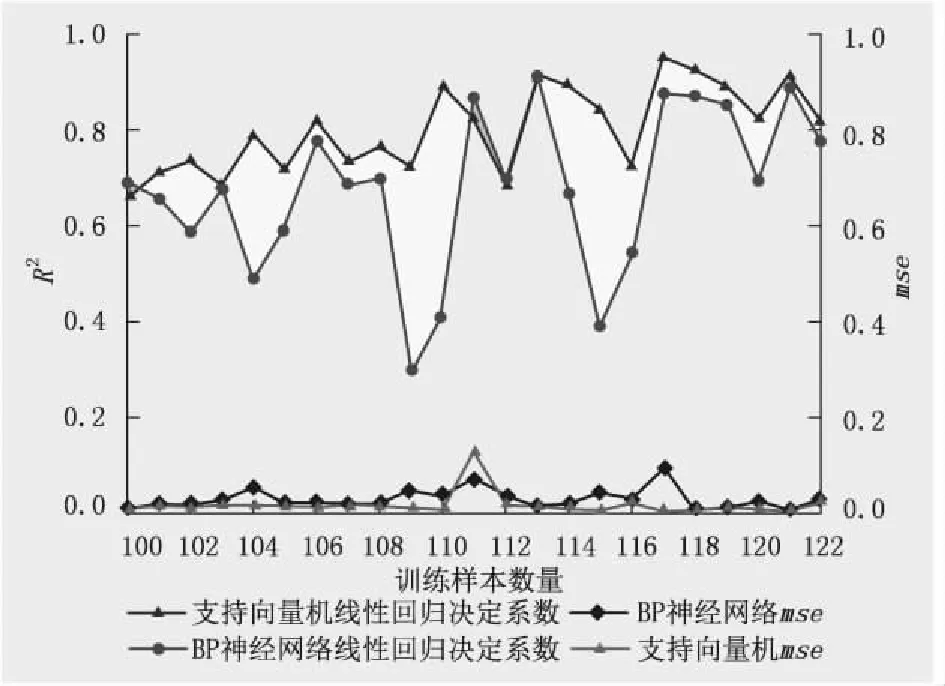
图1 不同训练样本数量下的SVM与BP神经网络 预测模型的评价参数值Fig.1 The evaluation parameters of SVM and BP neural network prediction models with different number of training samples
从预测误差来看,支持向量机模型的mse值基本处于较低的范围内,对比而言,BP神经网络的mse值波动幅度较大且数值较高。在训练样本数量为121时,支持向量机模型的mse值最低,mse最小值为0.003;在训练样本数量为118时,BP神经网络模型的mse值最低,mse最小值为0.007。
对比图1中2个评价参数曲线可知,支持向量机模型的R2值基本在BP神经网络模型之上,而mse值相反,因此,支持向量机模型的稳定性和精确度都要优于BP神经网络模型。综合考虑mse和R22个评价指标,选用mse值较小且R2值较大的模型为最优模型。对于支持向量机模型来说,优选出训练样本数量为118,测试样本数量为14,此时模型训练集拟合结果中R2为0.925,mse值为0.004;对于BP神经网络模型,优选出训练样本数量为121,测试样本数量为11,此时模型训练集拟合结果中R2为0.892,mse值为0.009。
3 结果与讨论
3.1 预测首年累计产量
利用上述优选的支持向量机模型,预测目标区块气井首年累计产量,通过对比实际产量值,支持向量机预测模型的测试集拟合结果的R2为0.927,mse为0.005。根据SVM产量预测模型结果可知:在训练集中,预测结果与实际数据点基本重合,训练效果拟合较好(图2);在测试集中,模型在预测产量上表现出较高的拟合精度,与实际产量趋势线基本一致,数值也较为接近(图3)。
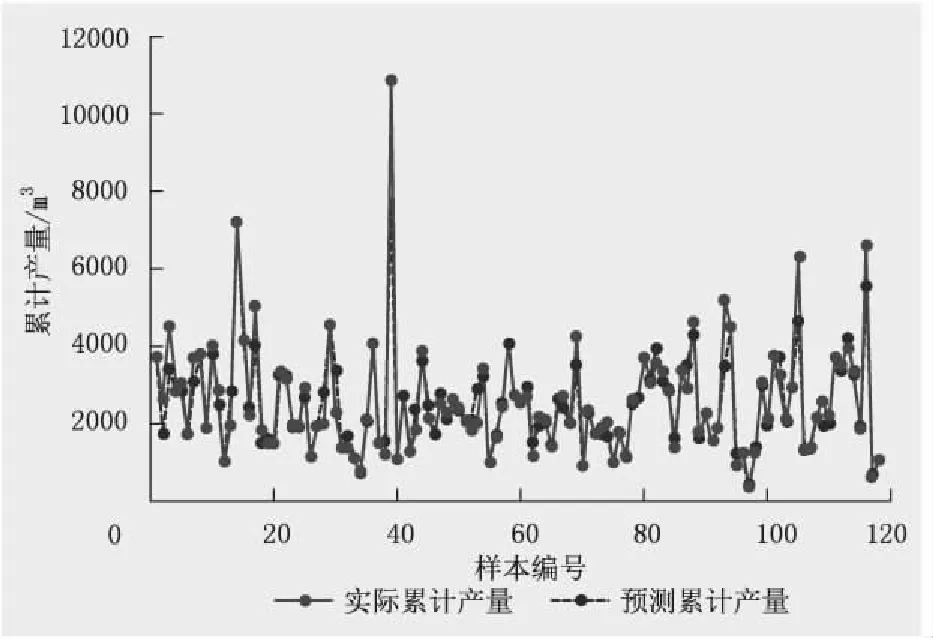
图2 SVM预测模型的训练集拟合结果Fig.2 The fitting results of training set of SVM prediction model

图3 SVM预测模型的测试集中预测值与实际值对比 (mse=0.005,R2=0.927)Fig.3 The comparison between predicted and actual values in the test set of SVM prediction model (mse=0.005, R2=0.927)
利用上述优选的BP神经网络预测模型,预测目标区块气井首年累计产量,通过对比实际产量值表明,BP神经网络预测模型的测试集拟合结果的R2为0.892,mse为0.009。根据BP神经网络产量预测模型返回的数据可以看出,在训练集中,实际产量与预测产量较为吻合,但存在一定的误差(图4);在测试集中,模型在预测产量时与真实值趋势基本一致,数值较为接近(图5)。

图4 BP预测模型的训练集拟合结果Fig.4 The fitting results of training set of BP prediction model
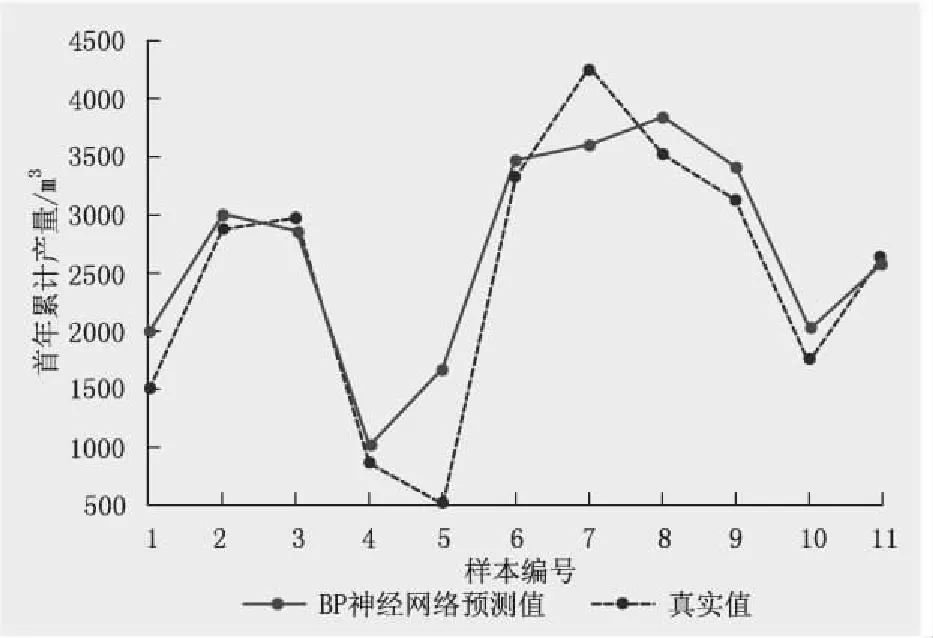
图5 BP神经网络预测模型的测试集中预测值与实际值 对比(mse=0.009,R2=0.892)Fig.5 The comparison between predicted and actual values in test set of BP neural network prediction model (mse=0.009, R2=0.892)
根据研究区的单井实际资料,由经验法拟合的气井首年平均日产量与测试产量的相关系数为0.746,产量预测模型公式如式(23)所示,拟合曲线如图6所示。
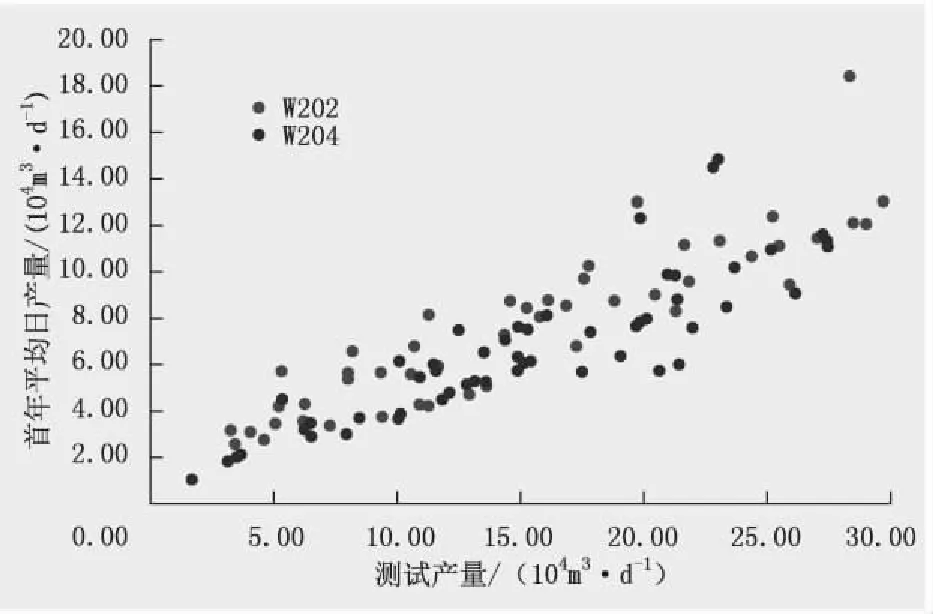
图6 研究区气井首年平均日产量与测试产量关系Fig.6 The relationship between average daily production and test production of gas wells in study area in the first year
Y=0.4499Xa
(21)
式中:Y为首年平均日产量,104m3/d;Xa为测试日产量,104m3/d。
由式(23)可预测研究区单井首年累计产量,将其与实际首年累计产量数据进行可视化对比处理(图7)。图7可知,由经验公式所预测的首年累计产量与实际产量之间存在一定偏差,R2为0.805,mse为0.025。
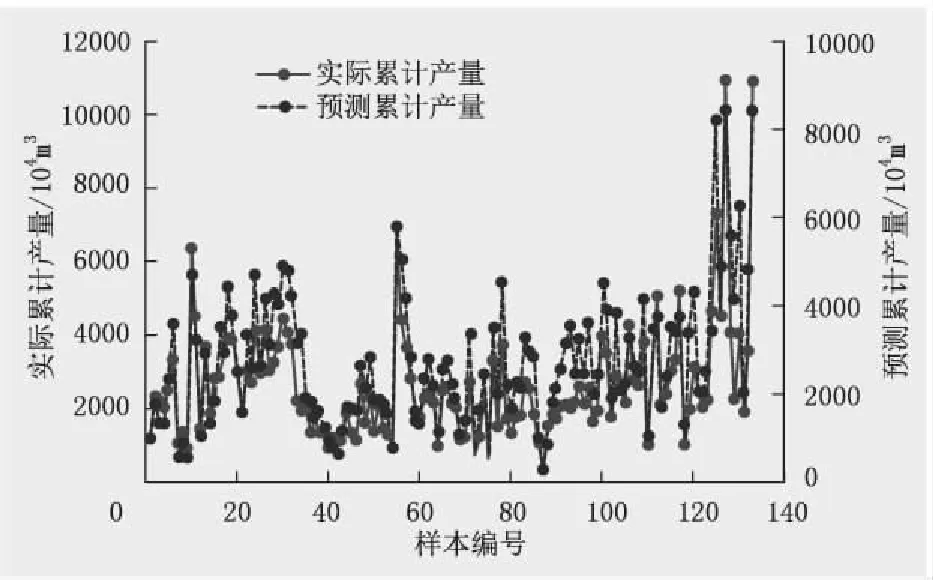
图7 经验拟合法实际值与预测结果对比 (mse=0.025,R2=0.805)Fig.7 The comparison between the actual value of empirical fitting method and the predicted result (mse=0.025, R2=0.805)
通过上述3个模型的预测结果对比分析表明(表2),SVM模型的预测结果与实际累计产量的趋势基本一致,均方误差结果最小,线性回归决定系数最大,比BP神经网络模型和传统经验公式法预测得更为准确。采用经验公式求得的首年累计产量预测值的均方误差较大,线性回归决定系数较小,较上述2个机器学习模型来说预测精度较低。总体来看,SVM模型对于研究区首年气井累计产量的预测效果较好,精度较高。

表2 SVM、BP神经网络及经验公式预测结果指标对比Table 2 The comparison of prediction result indicators of SVM, BP neural network and empirical formula
3.2 预测初期产量
利用支持向量机模型预测研究区气井初期产量(前期产量稳定后30 d平均日产量),通过对比实际产量值,支持向量机预测模型的测试集拟合结果的R2为0.883,mse为0.010。根据SVM产量预测模型结果可知,在训练集中,预测结果与实际数据点基本重合,训练效果拟合较好(图8);在测试集中,模型在预测产量上表现出较高的拟合精度,与实际初期产量趋势线基本一致,数值也较为接近(图9)。
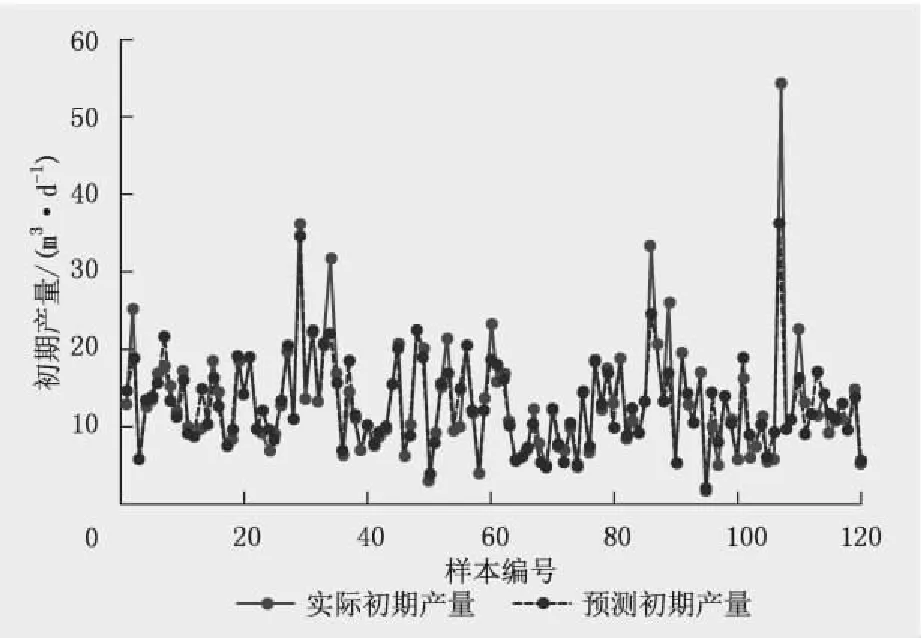
图8 SVM预测模型的训练集拟合结果Fig.8 The fitting results of training set of SVM prediction model
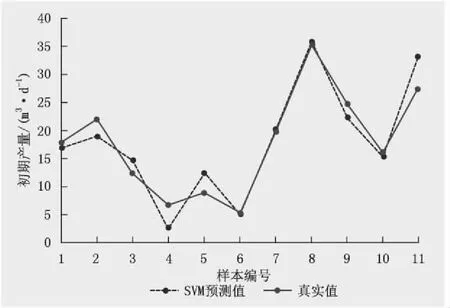
图9 SVM预测模型的测试集中预测值与实际值对比 (mse=0.012,R2=0.863)Fig.9 The comparison between predicted and actual values in the test set of SVM prediction model (mse=0.012, R2=0.863)
利用BP神经网络预测模型预测研究区气井初期产量,通过对比实际产量值得到,BP神经网络预测模型的测试集拟合结果的R2为0.863,mse为0.012。根据BP神经网络产量预测模型上返回的数据可以看出,在训练集中,实际产量与预测产量较为吻合,但有一定的误差存在(图10);在测试集中,模型在预测产量时与真实值趋势基本一致,数值较为接近(图11)。

图10 BP预测模型的训练集拟合结果Fig.10 The fitting results of training set of BP prediction model
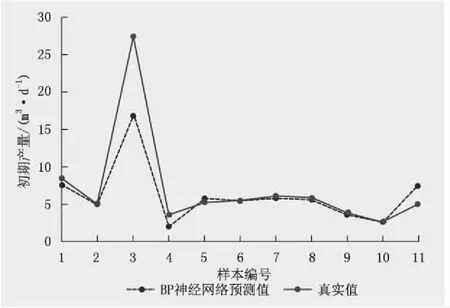
图11 BP神经网络预测模型的测试集中预测值与实际值 对比(mse=0.140,R2=0.900)Fig.11 The comparison between predicted and actual values in test set of BP neural network prediction model (mse=0.140, R2=0.900)
通过上述2个模型的预测结果对比分析结果可以看出(表3),SVM模型的预测结果与实际初期产量的趋势基本一致,均方误差结果最小,线性回归决定系数最大,其预测结果较BP神经网络模型和传统经验公式法预测得更为准确。总体来看,SVM模型对于研究区初期产量的预测效果较好,精度较高。

表3 SVM、BP神经网络及经验公式预测结果指标对比Table 3 The comparison of prediction result indicators of SVM, BP neural network and empirical formula
3.3 预测单井采出程度
利用支持向量机模型预测目标区块气井采出程度,通过对比递减法计算的采出程度,支持向量机预测模型预测的平均误差为4.14%(表4)。根据SVM采出程度预测结果,与递减法计算的采出程度基本一致。

表4 递减法计算及SVM预测采出程度结果指标对比Table 4 Comparison of results and indicators of the recursive calculation and SVM prediction of recovery percent
4 结 论
(1) 采用灰色关联法,考虑了地质因素、工程因素及生产数据,影响产量的主控因素为水平井垂深的中值、孔隙度、压力系数、压裂段长度、压裂改造段数等因素。应用SVM和BP神经网络法建立了产量预测模型,SVM模型更适用于研究区。
(2) SVM实现了基于数据分析方法的页岩气井首年累计产量及初期产量的准确预测。与BP神经网络、传统经验公式预测方法相比,SVM显示出了良好的预测能力和较小的误差,能够快速分析并准确预测气井的首年累计产量。与传统数值模拟软件相比,SVM模型不需要建立物理模型,基于有限的静态数据,就能够快速得到精度较高的产量预测结果。SVM模型可以进一步对压裂参数进行优化设计,为后期评价气井递减规律、计算气井单井可采储量提供可靠的数据,对其他页岩气区块的开发和产能评价也有着重要的借鉴指导意义。

