股线扭角和温度对导线综合系数取值影响的有限元仿真及应用
包华,豆云龙,邵汉杰,兰志文*,黄模佳
(1.中国能源建设集团安徽省电力设计院有限公司,安徽 合肥 230092;2.南昌大学工程力学系,江西 南昌 330031)
钢芯铝绞导线作为架空导线的主要产品之一,具有结构简单、架设和维护方便、线路造价低、传输容量大等优点。因此在各种的架空输配电线路中得到广泛应用。钢芯铝绞导线的综合弹性模量和热膨胀系数(以下简称综合系数)是架空导线力学计算中的重要参数,其取值误差会影响到导线应力、弧垂的准确计算,从而对输电线路的安全运行造成影响。
针对钢芯铝绞导线的综合系数国内外研究人员作了以下研究。Knapp[1]推导了导线受张力和扭矩作用下的刚度矩阵,完成对比实验,实验结果与理论非常一致。孟遂民[2]建立了忽略扭角摩擦挤压时的导线直股模型,推导得到了导线轴向综合弹性系数和轴向综合热膨胀系数的传统计算公式。邵天晓[3]通过建立股线分别在张拉荷载和温度单独作用下的力学模型,得到考虑扭角的导线综合系数计算表达式。并分析了传统计算公式与考虑扭角的计算公式之间的误差。李永平等[4]通过推导导线的抗弯、抗拉刚度,间接得到考虑股线扭角和泊松比的导线的综合弹性模量计算公式;并选取典型导线得到传统计算公式与考虑扭角泊松比的综合弹性系数之间的修正系数为0.88。张秋桦[5]通过建立股线的受力平衡方程,得到张拉导线的应力分布情况以及截面拉伸刚度理论值,通过有限元仿真和试验对比验证。李永平等[6]从导线几何特性的组成规律入手,从而找出导线各参数间的关系。由股线的受力分析导线的受力情况,分析股线的轴向应变,并建立非正交各向异性导线的刚度矩阵,得出绞制导线具有刚度不对称特性和较强的耦合效应。Raoof等[7]通过研究多层绞线的拉伸-扭转计算不同股线刚度的方法,其结果可应用于以导线半径、股线螺旋角为参数的多层股线螺旋结构的研究。
现行工程设计中导线综合弹性模量和热膨胀系数没有考虑温度及导线结构的影响,仅按照铝钢面积比及自身材料参数确定,而实际上,综合弹性模量和热膨胀系数是导线结构参数,由此会造成导线张力弧垂设计计算存在一定的误差。
本文将开展股线扭角对钢芯铝绞导线综合弹性模量和热膨胀系数的影响进行理论分析;通过有限元仿真,分析股线间摩擦、挤压和导线运行温度对绞线结构的影响,得到综合系数的数值解;结合工程实例,对比研究综合系数的理论解和数值解对导线张力与弧垂计算精度的影响。
1 综合系数计算理论
1.1 工程设计中综合系数计算方法
综合弹性模量在工程应用中常采用传统计算方法,即导线在纯拉伸状态下,假设钢芯和铝股轴向弹性伸长相同,根据力学基本理论,可以得到综合弹性模量公式如下:
(1)
式中:As为钢芯总面积,mm2;Aa为铝股总面积,mm2;Ea为铝股弹性模量,MPa;Es为钢芯弹性模量,MPa。
轴向综合热膨胀系数是钢芯铝绞导线仅在温度作用下时,由于钢芯和铝股是紧密绞合在一起的,伸长量相同;此时根据铝股所受的压力与钢芯所受的拉力在数值上相等,得到钢芯铝绞导线综合热膨胀系数:
(2)
式中:αa为铝股热膨胀系数,℃-1;αs为钢芯热膨胀系数,℃-1。
1.2 考虑股线扭角的导线综合弹性模量理论计算
钢芯铝绞导线是由多股铝绞线和钢芯扭成绞线,并不是由单一材料制成;同时受拉力后导线轴向的伸长量与线股方向的伸长量是不同的,从而使得钢芯铝绞导线的综合弹性模量与单股线的弹性模量不同。图1为导线结构及股线展开图,捻角βn为导线力学计算的重要结构参数。
由图1可知,捻角基本关系式为
tanβn=2πRn/Pn
(3)
节径比定义:mn=Pn/Dn及Dn=2Rn+dn,综上得到钢芯铝绞导线绞线的捻角计算表达式:
式中:βn为第n层上股线的捻角,以右旋方向为正;dn为第n层上股线的直径;Dn为第n股层的直径;mn为第n层的节径比。
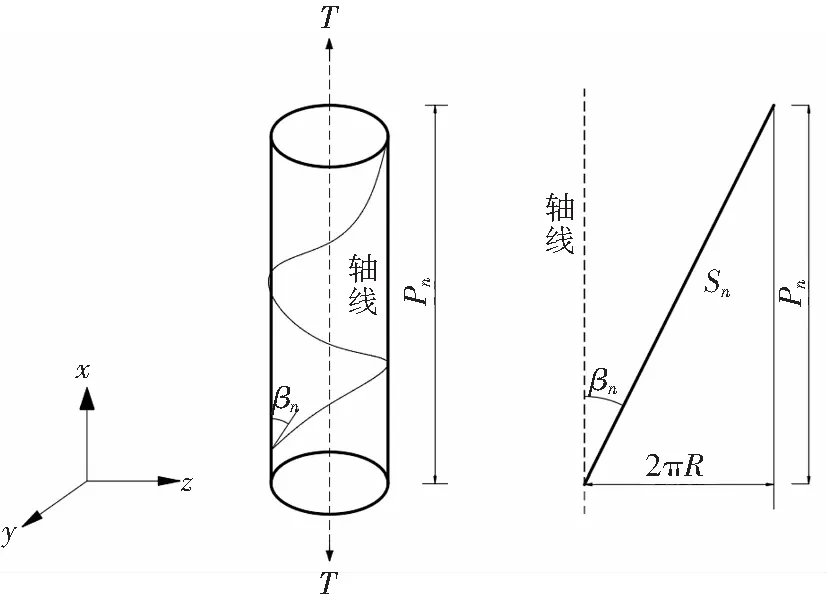
图1 导线结构图及股线展开图Fig.1 Wire structure diagram and strand expansion diagram
图2所示一个节距为l的单股线受拉伸长展开图。
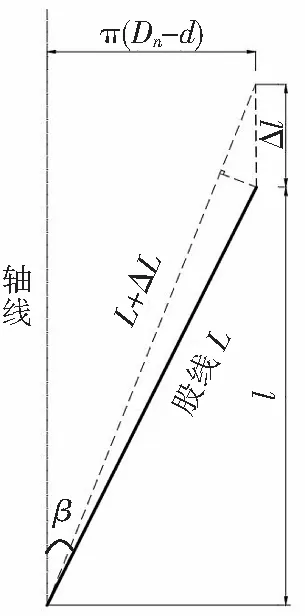
图2 单股绞线受拉伸长展开图Fig 2 Elongation expansion of single strand strand under tension
节距l对应的线股未受力前的长度L为:
(4)
当绞线受到轴向拉力后各股线均产生相同的轴向弹性伸长Δl,线股长度由L变成L+ΔL,L与l之间的关系,利用上式对L和l微分取近似值为:
(5)
线股的伸长率可写为:
(6)
式中:ε为线股的轴向伸长率,要比股向伸长率要大。
钢芯铝绞导线导线在温度和张力作用下,导线轴向方向满足变形协调,即各股线具有相同的轴向伸长率:
(7)
式中:T为导线张力;E为导线综合弹性模量;A为导线截面面积;α为导线轴向综合热膨胀系数;θi为导线某一状态温度;θ0为导线制造温度,一般取20 ℃。
综合弹性模量表达式为:
(8)
1.3 考虑股线扭角导线综合热膨胀系数计算方法
整根绞线当前线温θi与制造温度θ0温差为Δθ,各层线股沿轴向均应有温差引起的相同的伸缩率,则第x层股线轴向伸长:
(9)
第x层股线股向伸长:
(10)
(11)
式(10)中线股伸长εx不同于式(11)中的整根绞线的轴向伸长ε,为了使其相同,该线股必然受到其他线股的约束,从而减少轴向自由伸缩率Δεx,则
(12)
线股所减少的自由伸缩率Δεx,必然引起线股轴向压、拉内应力。其整根绞线各股压、拉内应力的总和应为零。则整根绞线各股内应力总和可写为:
(13)
整根导线的轴向综合温度线膨胀系数α[3]计算公式为:
(14)
2 考虑温度效应的导线综合系数有限元仿真
2.1 导线几何模型及材料参数
选用导线型号为小截面导线JL/G1A-400/35和大截面导线AACR/EST-500/227,钢芯的弹性模量为190 GPa,泊松比为0.3,热膨胀系数为11.5×10-6℃-1;铝股的弹性模量为55 GPa,泊松比为0.3,热膨胀系数为23×10-6℃-1;导线的几何参数如表1和表2所示。
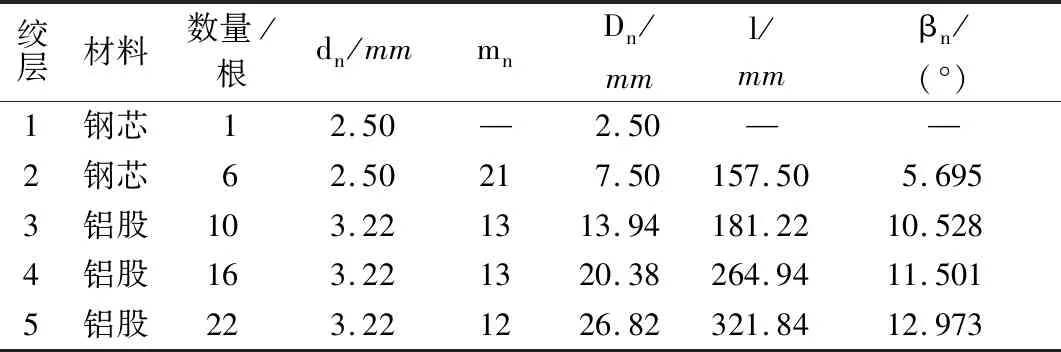
表1 钢芯铝绞导线JL/G1A-400/35几何建模参数Tab.1 Geometric parameters of steel-cored aluminum stranded wire JL/G1A-400/35
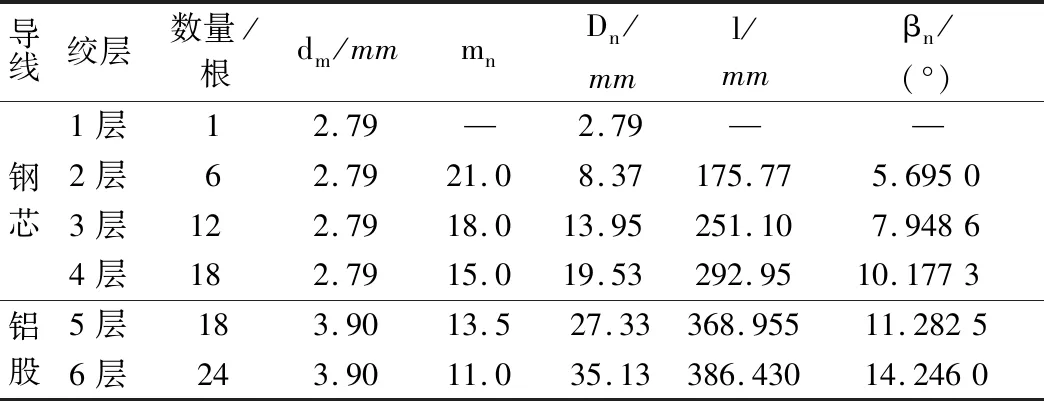
表2 AACR/EST-500/227型导线几何参数Tab.2 Geometric parameters of AACR/EST-500/227 conductors
2.2 网格划分及边界条件
在Solid Works中完成导线JL/G1A-400/35的几何模型,导入到ANSYS中进行有限元分析。取导线长度为100 mm,并划分网格如图3和图4所示。

图3 JL/G1A-400/35导线轴向网格划分及截面网格划分Fig.3 Axial mesh division and section mesh division of JL/G1A-400/35 conductor

图4 AACR/EST-500/227导线轴向网格划分及截面网格划分Fig.4 Axial and cross section meshing of AACR/EST-500/227 conductors
接触和边界条件设置:将股线间的摩擦系数设为0.3;约束导线端部x=0 mm截面上设置固定端,约束X、Y、Z3个方向上的全部自由度;仅考虑导线对称轴向(x方向)受拉,忽略重力影响。在导线另一端x=100 mm截面建立刚性域,保证x=100 mm截面上节点沿轴向位移相同;最后在x=100 mm截面上施加集中力。
2.3 考虑温度效应导线综合系数有限元分析
在Solid Works中完成导线JL/G1A-400/35、AACR/EST-500/227的几何模型,导入到有限元仿真软件中进行仿真分析。
(1) 导线综合弹性模量有限元仿真。
施加温度和根据状态方程(15)计算所得对应温度下导线张力,输出导线截面力应变,根据式(8)计算得到不同温度下导线的综合弹性模量如图5所示。
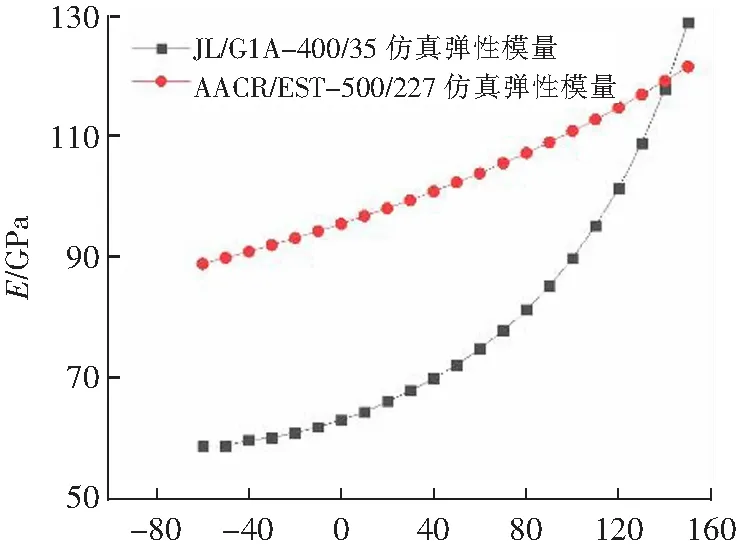
θ/℃图5 导线综合弹性模量随温度变化图Fig.5 Composite elastic modulus of wire changes with temperature
由图5可以得知,导线综合弹性模量的有限元仿真值随温度的增加而增加,温度每增加10 ℃,综合弹性模量大约增加2~3 GPa;当温度达到某一温度(拐点温度)时,综合弹性模量将与钢芯的弹模一致。
(2) 导线综合轴向热膨胀系数。
建模:导线一端固定,一端自由;仅在温度作用下输出导线变形,在不同分析步下导线整体施加不同温度,环境温度设置为20 ℃,得到导线截面平均应变,进而求出导线轴向综合系数随温度变化,如图6所示。
由图6可知,导线轴向综合热膨胀系数有限元仿真值与理论值接近,误差较小,说明理论计算值和有限元仿真的正确性;以及导线轴向综合热膨胀系数温度无关。
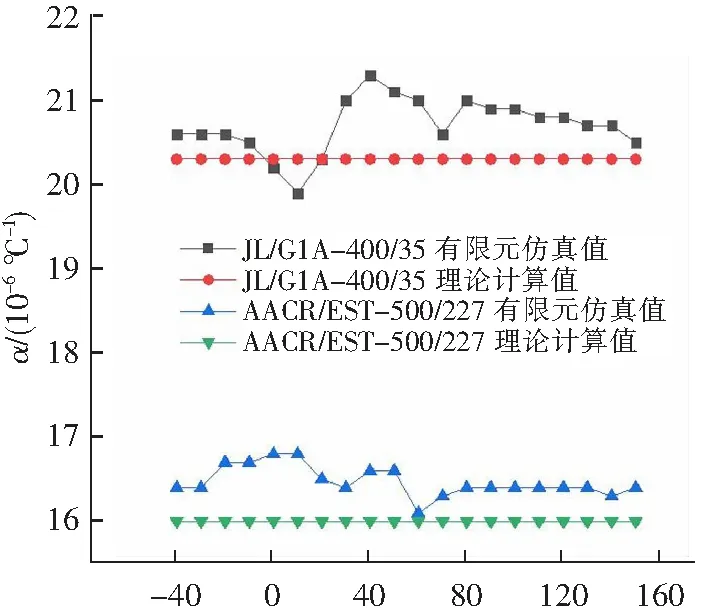
θ/℃图6 导线轴向综合热膨胀系数随温度变化图FIg.6 Variation of axial comprehensive thermal expansion coefficient of wire with temperature
3 工程实例
3.1 导线状态方程
描述导线在不同气象条件下的应力变化的方程为导线状态方程,常用状态方程为斜抛物线状态方程。已知θ1温度下导线的平均应力σ01,根据不等高悬点架空线状态方程[3]式(15),得到θ2温度下导线的平均应力σ02:
(15)
式中:σ01、σ02分别为2种状态下架空线弧垂最低点处的应力;γ1、γ2分别为2种状态下架空线的比载;θ1、θ2分别为2种状态下架空线的温度;l、β分别为该档的档距和高差角;α、E分别为架空线的轴向综合温度膨胀系数和综合弹性模量。
3.2 工程实例计算
某工程实例,导线的基本参数和线路工程力学指标如表3,表中l为档距,h为高差,A为面积。

表3 导线类型及线路工程参数Tab.3 Wire types and line engineering parameters
3.3 弧垂应力误差分析
以实际工程为例,以20 ℃和20%RTS(额定拉断力)作为气象条件的初始条件,通过将综合弹性模量的理论公式和有限元仿真值分别代入状态方程和悬链线方程,得到导线平均运行应力和弧垂的理论计算值和有限元仿真值,结果如表4所示。
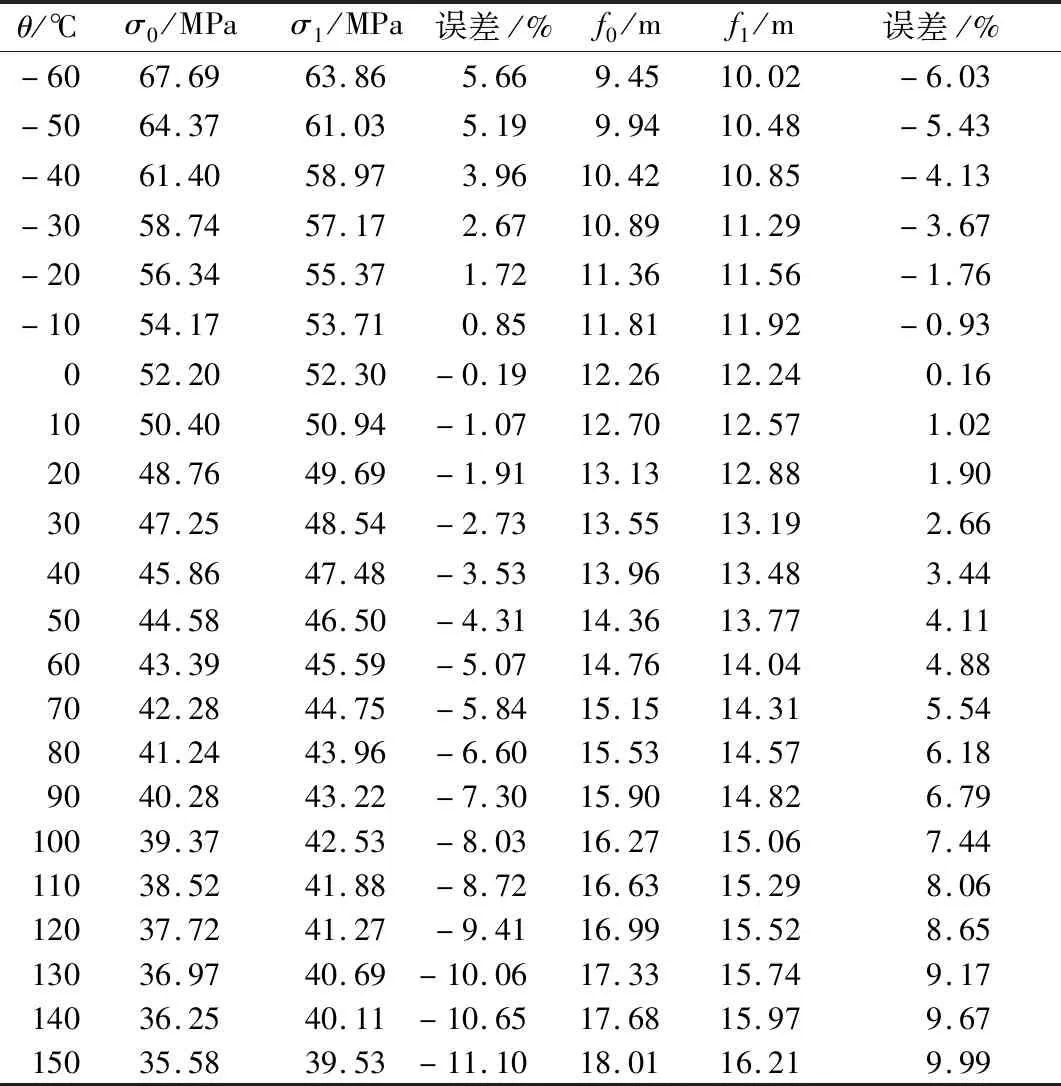
表4 JL/G1A-400/35理论与有限元弧垂应力误差分析(20%RTS)Table.4 JL/G1A-400/35 theory and finite element error analysis of sag stress (20%RTS)
为更加生动显示导线综合系数取值对弧垂应力计算的影响,随将表4所示数据,导入到绘图软件中得到不同温度下弧垂、应力的理论值与有限元值对比分析图,如图7所示。
将AACR/EST-500/227导线综合弹性模量的理论公式和有限元仿真值分别代入状态方程和悬链线方程,得到导线弧垂应力随温度变化的理论值和有限元值对比情况,结果如表5所示。
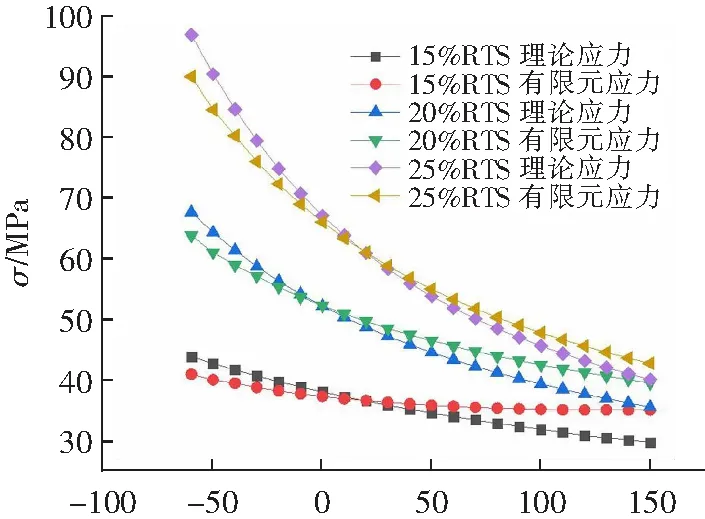
θ/℃(a) 平均应力随温度变化图
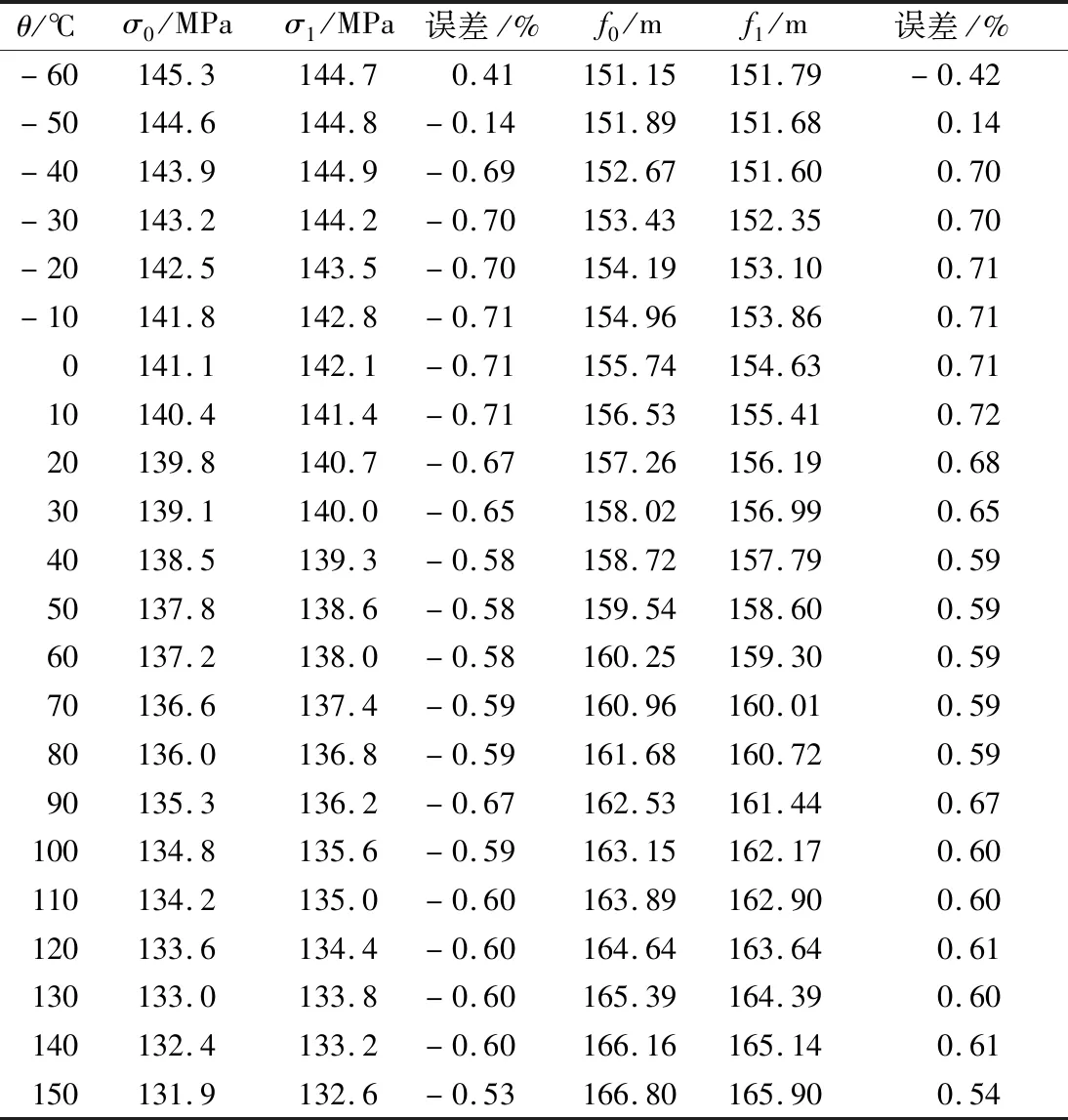
表5 AACR/EST-500/227理论与有限元弧垂应力误差分析(20%RTS)Table.5 AACR/EST-500/227 theory and finite element sag stress error analysis (20%RTS)
为更加生动显示导线综合系数取值对弧垂应力计算的影响,随将表5所示数据,导入到绘图软件中得到不同温度下弧垂、应力的理论值与有限元值对比分析图,如图8所示。
由图7、图8可知:将综合弹性模量的传统理论值和有限元仿真值分别代入状态方程和悬链线方程,对比分析导线平均运行应力和弧垂的传统理论计算值和有限元仿真值所存在的差别。对于小档距40 m的小截面导线JL/G1A-400/35的,平均运行应力和跨中弧垂的传统计算值较有限元值在高温阶段(80 ℃)存在一定误差(大于5%);对于大跨越2 000 m选用的大截面导线AACR/EST-500/227,平均运行应力、弧垂的传统计算值较有限元值误差均小于1%。这说明综合系数取值对弧垂和应力准确计算的影响,对于小档距小截面导线影响较大,对于大档距大截面导线影响较小。
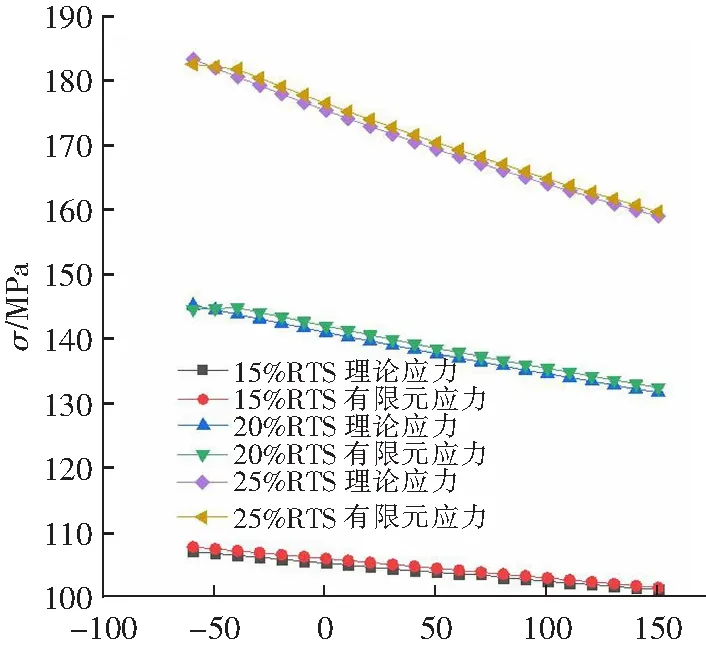
θ/℃(a) 平均应力随温度变化图
4 结论
本文通过推导得到了基于股线扭角和温度对导线综合系数取值影响的理论计算公式,并通过有限元仿真研究了在温度和张力共同作用下绞线结构松紧程度对综合系数取值的影响,结合综合系数在实际工程中应用,得到如下结论:
(1)导线轴向综合热膨胀系数传统理论值与有限元仿真值误差均在2%以内,数值仿真的结果表明,导线轴向综合热膨胀系数不随温度变化。
(2)数值仿真的结果均表明导线综合弹性模量随着温度的变化而变化,对于所选择的常用钢芯铝绞导线,温度每升高10 ℃,综合弹性模量约增加2~3 GPa。
(3)对于小档距40 m的小截面导线JL/G1A-400/35的,平均运行应力和跨中弧垂的传统计算值较有限元值在高温阶段(80 ℃)存在一定误差(大于5%);对于大跨越2 000 m选用的大截面导线AACR/EST-500/227,平均运行应力、弧垂的传统计算值较有限元值误差均小于5%。
(4)考虑温度效应下综合系数的不同取值,在最高设计运行温度时,小档距小截面输电线路弧垂应力存在大于5%的计算误差,大档距大截面输电线路弧垂应力计算误差小于1%。

