均匀流作用下海洋悬链线立管的振动特性研究

赵 林，褚凯丽，张无际

（中国海洋大学工程学院，山东 青岛 266100）

柔性圆柱涡激振动数值模拟对计算资源要求较高，当前国内外对圆柱涡激振动的研究主要开展二维模拟或采用切片法开展准三维模拟，而运用三维直接数值模拟方法开展的相关研究有限，且在均匀流下对悬链线立管相关研究有局限性。本文采用水动力软件OrcaFlex对均匀来流下细长柔性立管涡激振动进行三维数值模拟，探究外流流速和流向的改变对柔性立管的动力响应规律的影响，意在为海洋柔性立管的设计安装和研究立管涡激振动提供一定的参考价值。1所示，并认为所有的外载荷仅仅作用在节点上，节点间的部分可等效于各种弹簧阻尼器，用来模拟线的结构特性，即根据应力变关系与节点瞬时位置的变化得到缆体的张力。

1 理论基础

在OrcaFlex中，缆线采用集中质量模型代表。将缆线看作由一系列的节点构成，仅节点具有质量，且节点间通过无质量的弹性单元相互连接如图

OrcaFlex中有效张力表达式如式（1）所示。

式中，Te为有效张力；p0为外部压力；a0为管线横截面积；pi为内部压力；ai为内管横截面积。相邻两节点间管壁张力与有效张力相对关系见图2。

图2中Tw表示壁面张力，表达式为式（2）。

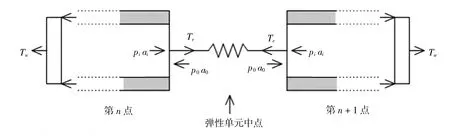
图2 有效张力示意图

式中，EAε由模型段轴向刚度引起；2ν（p0a0-piai）由模型段的内部、外部压力产生，准确讲是由泊松比的影响产生；EAe（dl/dt）/L0由模型段轴向阻尼引起。EA为模型轴向刚度；ε=（L-λL0）/λL0为总轴向的平均应变；λ为微小管段伸长系数；L0为模型段原长；ν为泊松比；e为模型段阻尼系数，dl/dt为模型段长度改变速率。

2 模型建立与验证

2.1 模型建立

使用Orcaflex软件建模研究立管在不同均匀流作用下立管的振动特性分析，水流流向沿X负方向定义为正向流，沿X正方向定义为反向流。柔性立管数值模型如图3所示，立管基本参数见表1。

大学较之中学存在阶段性的差别，主要表现在学习和人际交往上。新生中主要的问题之一是学习问题，不少新生来访者主诉“学习内容比较枯燥，没意思”，“不知道学这些东西有什么用，对现在的学习很迷茫”，“担心未来的发展，不知道将来自己要做什么，能做什么”。大学新生学习上的迷茫感主要表现三个方面。

图3 OracFlex建模示意图

表1 立管基本参数

2.2 模型验证

通过将数值模拟结果与已有的物模试验结果进行对比，来验证建立数值模型的准确性。中国海洋大学的重点实验室对立管涡激振动特性进行了试验研究，下面将对其顶张力T=0.04 kN，流速v=0.2 m/s的均匀流试验工况进行数值模拟，将得到的响应模态和响应频谱结果和试验结果开展比对，验证了本文建立的数值模型的有效性。

图4为试验及本文数值模拟的立管IL、CF方向模态对比结果，其中IL方向的无量纲振幅已经消除因流体作用产生的位移及立管悬链线姿态的静态位形的影响。通过对比得出，数值模拟得到的柔性立管的CF、IL方向响应模态阶数与物理模型试验结果一致，依次为2、3阶。

图4 立管管CF、IL方向振动模态（D为立管直径，A为立管振幅值）

由于不同时间段内功率谱密度大小不同，为方便对比分析，选取和物理模型试验中相同位置的5个点位10 s内的频谱数据与物理模型试验结果进行对比，这5个位置分别为Z/L=1/6、1/3、1/2、2/3、5/6（Z为到立管端部的距离，L为立管模型长度）。由图4可知，在CF方向物模与数值模拟结果主导频率为1.563 Hz、1.620 Hz；在IL方向物模与数值模拟结果主导频率为3.125 Hz、3.240 Hz。对比发现，通过数值模拟得到的主导频率较试验稍微有些偏大，这是由于实际环境条件和软件中的理想环境有差异导致的，但误差小于5%，说明在软件中建立的柔性立管数值模型是可靠的。

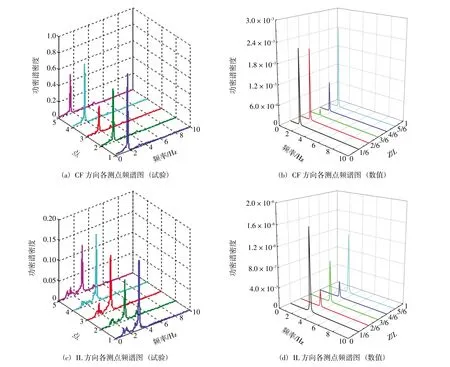
图5 响应频谱对比图

3 结果与分析

3.1 模态分析

因工况较多，故选取正反向流0.2～0.5 m/s进行分析。图6显示立管在流体作用下产生周期性振动，且在CF、IL方向上振动幅值和振动周期不同。由图6可知，海流流速分别为0.2 m/s、0.3 m/s、0.4 m/s、0.5 m/s时，立管CF方向的主导模态阶数分别为2、3、3、4，IL方向的结果比较复杂：流速为0.2 m/s时主导模态阶数为3；流速为0.3 m/s时5阶模态占优，存在2阶分量；流速为0.4 m/s时4阶模态占优，但同时存在非常强的2和4阶分量；流速为0.5 m/s时6阶模态占优。不同流速作用下，立管IL方向最大无量纲振幅分别为0.23 D、0.18 D、0.20 D、0.21 D，CF方向分别为1.24 D、1.20 D、1.24 D、1.21 D（其中D代表立管外径）。

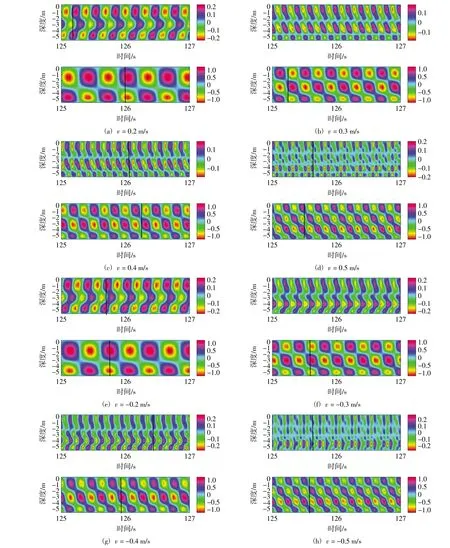
图6 不同流速下立管IL（上）、CF（下）方向位移空间时程分布图

流速为-0.2 m/s、-0.3 m/s、-0.4 m/s、-0.5 m/s时，立管CF方向的主导模态阶数分别为2、3、3、4，IL方向的结果同样比较复杂：流速为-0.2 m/s时，主导模态阶数为3；流速为-0.3 m/s时，同时存在1、4、5阶模态，其中1、5阶分量占比较强；流速为-0.4 m/s、-0.5 m/s时，4阶、3阶模态占优，但同时存在其他分量。显然立管IL方向上激发的主控模态结果与正向流作用下的结果不一致。不同流速作用下，立管IL方向的最大振幅为0.24 D、0.34 D、0.28 D、0.29 D，CF方向分别为1.25 D、1.20 D、1.26 D、1.24 D。

基于均匀流立管涡激振动产生的结果能够得出以下结论：立管IL方向位移小于CF方向，而立管IL方向激发的模态要远比CF方向模态复杂。从时程图中可以清晰地看出，低流速时立管CF、IL方向均呈现驻波特征，而随着流速增大，IL方向出现行波。

图7为海洋柔性立管在不同来流流向和速度条件下，Z/L=1/2位置10 s内的位移数据通过快速傅里叶变换求得的频谱图。由图7可知，立管在不同流速的正、反向流作用下，IL与CF方向振动频率均呈现单谱模式，且沿立管轴向各点的频率值均没有变化。0.2～0.5 m/s流速作用下对应的立管CF主导频率分别为：1.620 Hz、2.499 Hz、3.11 Hz、4.029 Hz；IL方向的主导频率依次为：3.240 Hz、5.000 Hz、6.225 Hz、8.068 Hz；-0.5～-0.2 m/s流速作用下对应的立管CF方向主导频率依次为：1.6 Hz、2.61 Hz、3.21 Hz、4.05 Hz，IL方向主导频率依次为：3.21 Hz、5.21 Hz、6.38 Hz、8.10 Hz。

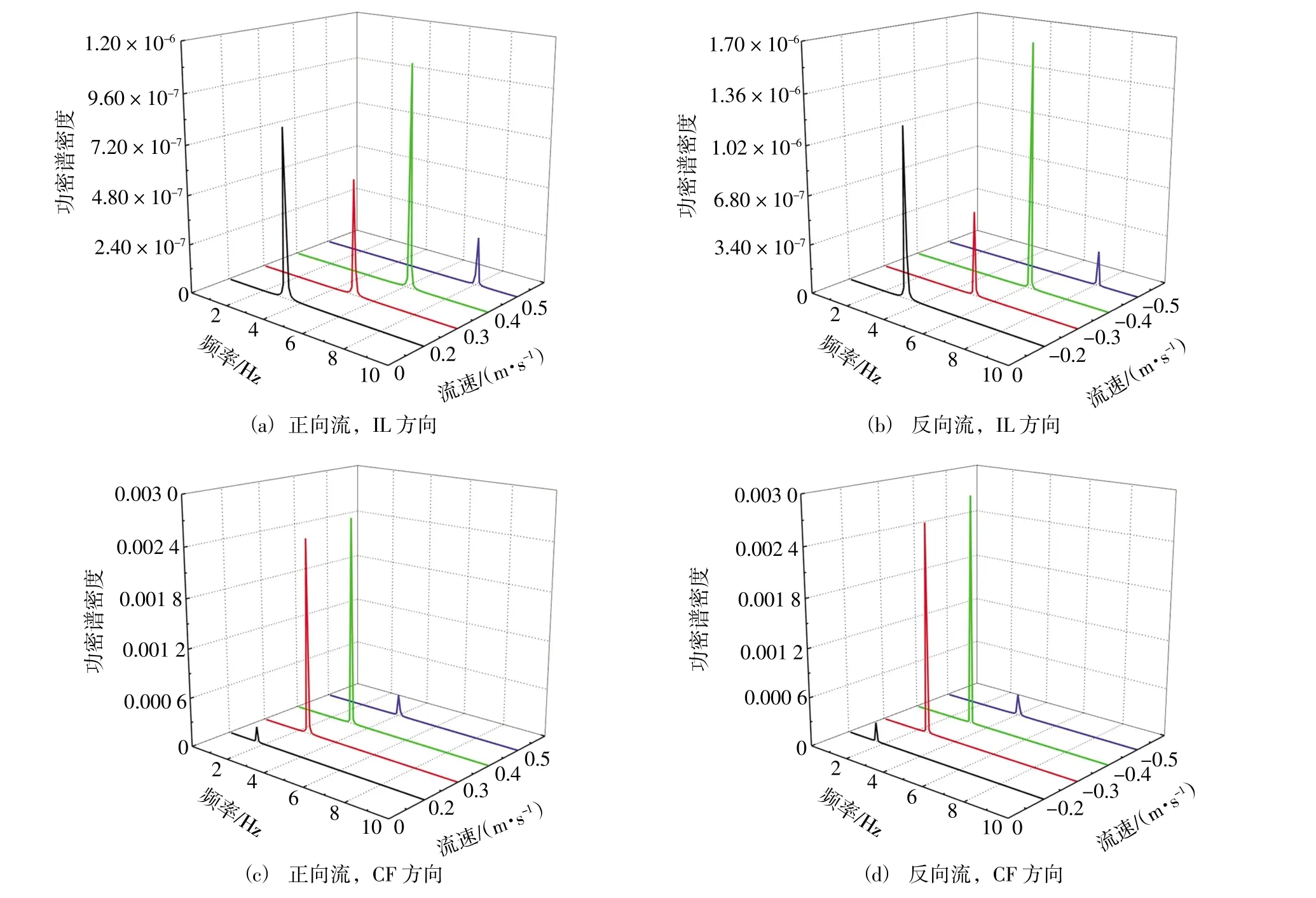
图7 正、反流向下立管IL、CF方向频谱图

由此可见立管CF、IL两个方向的响应频率均与作用流速成正相关，流向的改变对立管两个方向上的响应频率影响较小。立管IL与CF方向的主导频率比值为2与流向无关，且IL、CF方向的主导频率的功率谱密度值不同。

3.2 立管振动响应的空间形态分析

图8和图9分别为在正反流向作用下选取涡激振动稳定之后10 s内立管整体的运动轨迹并由此绘制立管三维图，其中顺流向的结果已经消除了立管悬链线姿态的静态位形，以及流体作用产生的位移影响。在立管模型的外表面上依次选取11个点，从水面至水底依次编号为1～11号点位，做这些点在x-y平面内50 s的运动轨迹。

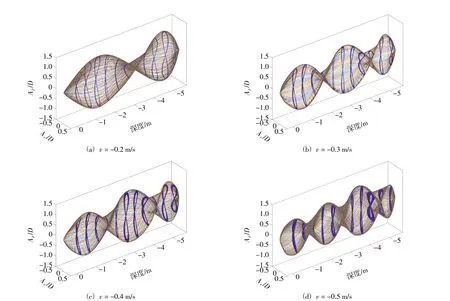
图9 反向流作用下的立管涡激振动三维图

由图8可知，0.2 m/s和0.4 m/s作用下，该段时间内线条（立管运动轨迹）在空间内的分布不均匀，如图8（a）所示多个线条抱团形成一个“组线条”，由大量的“组线条”构成立体图形。且此立体图形不是实体，而是线条在“8”字轨迹上形成的壳体，壳体内部无线条穿过，即立管运动轨迹不经过“8”字形内部空间。而0.3 m/s和0.5 m/s流速作用下，该段时间内线条在空间内的分布比较均匀，没有出现多个线条抱团形成一个组线条的现象。0.2～0.5 m/s流速作用下，三维图形依次在x-z、y-z平面内的投影在CF方向上分别呈现出明显的2、3、3、4阶主导模态特征，在IL方向上呈现的主导模态特征与本文第3.1节中0.2～0.5 m/s流速作用下模态分析的结果一致。

图8 正向流作用下的立管涡激振动三维图

由图9可知，不同于正向流各个流速作用下的结果，-0.5～-0.2 m/s的反向流速作用下该段时间内线条在空间内的分布都比较均匀，没有出现多个线条抱团形成一个组线条现象，虽然-0.3 m/s和-0.4 m/s流速作用下图形没有出现组线条现象，但形成的立体图形封闭性并不强。-0.5～-0.2 m/s流速作用下，三维图形依次在x-z、y-z平面内的投影在立管CF方向上分别呈现出明显的2阶、3阶、3阶、4阶主导模态特征，IL方向上呈现主导模态特征同样与上一章节中-0.5～-0.2 m/s流速作用下无量纲位移图结果一致，并与正向流的结果一致。

结合图8和图9来看，在正反向流作用下，图形在横流向占据的空间尺度较大，在顺流向占据的空间尺度比较小。不同流速作用下11个点的运动轨迹除个别点位的运动轨迹是“月牙”形、弯曲的“1”字形外，如图7（d）中的11号点位和图7（c）中的5号点位，其他都是“8”字形。轨迹图形的大小沿立管轴向呈现由小到大再由小到大的循环波动趋势，形成的“扭转节”（立管横流向位移明显减小的位置）个数越多循环次数越多。总体上，运动轨迹大的位于波腹处，轨迹小的位于“扭转节”位置。作用流速越大，运动轨迹越粗，这是因为流速变大，主导频率比值（为立管顺流向响应频率，为立管横流响应频率）开始偏离2，各点的运动轨迹逐渐不稳定。

在0.2 m/s流速作用下所有点的运动轨迹均是“8”字形的，虽然其大小、形状、弯曲方向不同，甚至更像是弯曲的“1”字形，但这是由各点处于立管的不同位置的决定的，并不改变其的“8”字形本质。以“8”字形的上半部分为研究对象，发现各点的绕行方向截然不同。自立管顶部开始1～4、8～11点位的绕行方向为顺时针，5～7点位为逆时针，可以发现绕行方向的变化比较频繁。而0.3 m/s流速作用下立管上11个点位的“8”字上半部分的绕向方向，自立管顶部开始，1～3、5～8点位的“8”字上半部分为顺时针绕向，仅4、9～11为逆时针。通过与0.2 m/s流速作用下的立管相同位置11个点位的绕行方向对比，发现这两个工况各点的绕行方向略有不同。由此可见，不同流速作用下各点的绕向方向有很大不同。

自立管顶部开始，-0.2 m/s流速作用下，4、5、7点位的绕行方向为顺时针，1～3、6、8～11为逆时针。与0.2 m/s正向流作用下的结果对比，发现各点位的绕行方向仅6号相同，且各点绕行方向变化比较频繁，可见流向的改变对各点的绕向方向有一定影响。不同于正向流中立体图形迎流侧外表面向外凸起且外表较为光顺而内侧大多向内凹陷的结果，反向流作用下结果与之相反，这些同样是由于“8”字形弯曲方向和轨迹形状的不同产生的。

3.3 立管振动响应的相位谱分析

由图10和图11可以看出：整个相位差—水深曲变化趋势比较复杂，相位差值随水深时而增大时而减小，变化十分剧烈，很难对其进行不同流速作用下的整体规律分析，因此分别对0.4 m/s与-0.4 m/s流速果进行讨论。

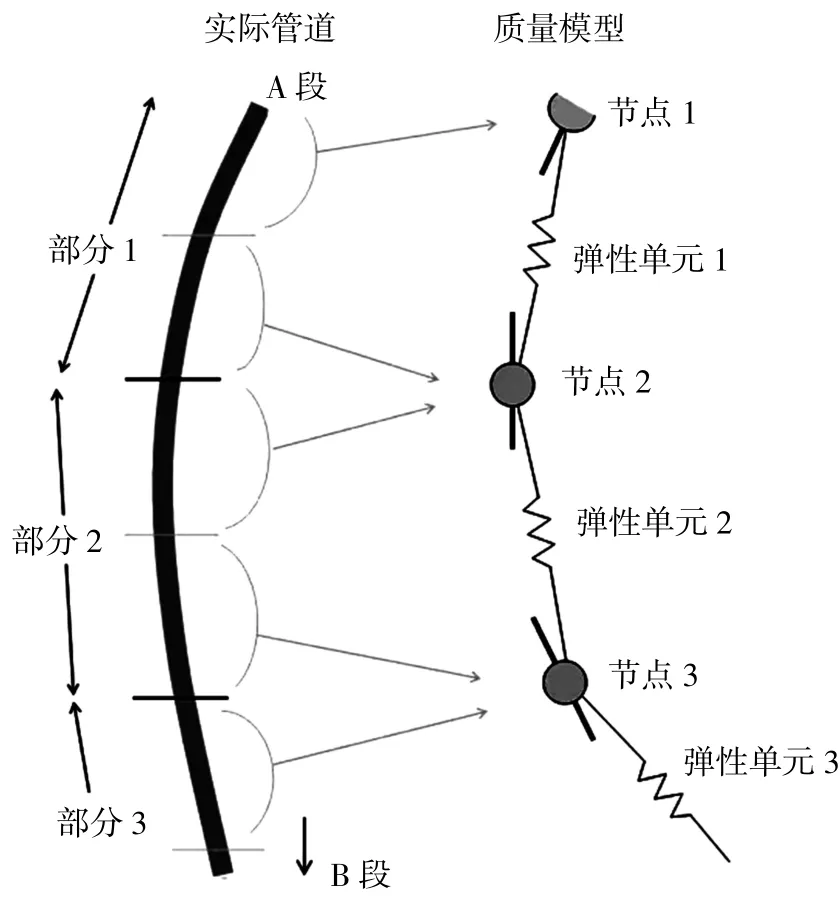
图1 集中质量原理示意图

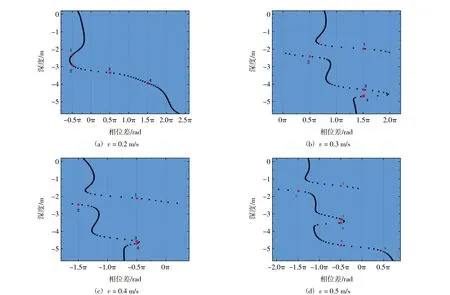
图10 正向流作用下立管CF、IL方向振动相位差随水深变化曲线图

图11 反向流作用下立管CF、IL方向振动相位差随水深变化曲线图

在0.4 m/s流速作用下，对比该流速下三维位移图和相位差图，发现“8”字形上半部分绕行方向变化对应的相位差值为-3π/2、-π/2、且这两个相位差值对应的4个水深值，分别在-2.2 m、-2.6 m、-4.9 m水深附近（用1、2、3、4在图中依次标出），这表示立管在发生稳态振动过程中“8”字形的绕向在整个水深范围内变化了4次。1点以上、2～3间和4点以下绕向相同，其余部分之间方向一样。对比图6中该点位对应水深处的立管x-y截面运动轨迹，发现该水深附近的运动轨迹接近弯曲的“月牙形”，这一点与李萨如图形（Lissajous-Figure）结果一致，说明求得的相位差是正确的。1～2之间对应的水深范围为0.4 m、3～4对应的水深范围不到0.1m，这表明绕行方向的改变十分迅速，在这样情况下除非是逐点对立管进行运动轨迹分析，否则很难观测到其绕行方向的改变，因此对立管进行相位差分析很有必要。

以-0.4 m/s流速作用下的结果为例：对比该流速下立管的三维位移图和相位差图，发现“8”字形上半部分绕行方向变化对应的相位差值为-5π/2、-3π/2、-π/2、π/2。且这两个相位差值对应5个水深值（分别用1、2、3、4、5在图中依次标出），这表明立管在发生稳定振动过程中“8”字形的绕行方向沿水深变化了5次。1～2点间、3～4点间绕行方向一致，其余部分之间方向一致。对比图9中该点位对应的水深处的立管x-y截面运动轨迹，发现该水深附近的运动轨迹接近弯曲的“月牙形”，说明求得的相位差是正确的。绕行方向改变的点对应的水深大小不同，1～2之间对应的水深深度为2.2 m、2～3对应的水深为0.3 m、3～4对应的水深为2.2 m、4～5对应的水深范围为0.3 m，这表明绕行方向的改变与管段长短无关。

4 结 论

通过以上数值模拟分析可得出以下结论。

（1）通过模态分析，得出均匀流作用下流速及流向的改变对柔性立管响应频率、模态阶数的影响程度不同。立管的响应频率和CF方向的响应模态阶数与流速成正相关，立管IL方向随流速增加呈现多阶模态，主导模态阶数并不一定随流速增大。流向的变化极大地改变了立管发生最大振动幅值的位置。

（2）通过立管振动响应的空间形态分析，得出立管的三维空间形态随着流速、流向的改变而呈现出不同的形式。作用流速越大立管的三维空间形态越是复杂，因绕z轴扭转而形成的“扭转节”越多，流向的改变不影响立管产生的旋转节个数。但“扭转节”占据的空间随水深及流速、流向变化，水深越大占据的空间越大，反向流“扭转节”占据的空间大于正向流的空间。因此，在立管设计安装时，应根据立管的所应用海域的潮汐变化情况，适当作出相应变化，以减少疲劳损伤。

（3）通过立管振动响应的空间形态与相位谱分析，得出立管的运动轨迹一般为“8”字形状，不同位置的“8”字形大小，绕行方向及弯曲方向不同。即便处于立管的同一位置，该位置处的运动轨迹随流速和流向的改变也呈现不同的弯曲方向和绕行方向。低流速时立管的运动轨迹较窄，流速增大时，开始偏离2，运动轨迹逐渐变得不稳定、运动轨迹逐渐加粗。通过对立管横流向、顺流向的相位、相位差进行研究确定了两个方向的相位差值决定立管运动轨迹的绕行方向和形状。