基于变分模态分解的结构裂纹识别*
杨启航, 李林安, 李利青, 米少瑄
(天津大学 机械工程学院,天津 300354)
引 言
我国经济建设的发展不断加快,城乡交通需求逐步增长,因而各式各样的桥梁也相继建成.与此同时,桥梁受到材料老化、过载、侵蚀和地震等因素不同程度的破坏,导致桥梁的承载能力、安全性和耐久性都在不断削弱.经过大量研究人员多年的不懈努力,提出了多种不同的桥梁结构检测方法.
总的来说,可以将桥梁结构检测方法分为基于完整有限元模型和不基于完整有限元模型的方法[1].前者主要面临的困难是获取准确完整的模型,然而一些旧桥已经使用了很多年,甚至连图纸都丢失了,这是根本无法实现的.后者没有这个问题,而是依赖于可靠的结构响应和先进的信号处理方法.
近年来,信号处理技术得到了不断的发展,不基于完整模型的方法得到了越来越多的研究,其中最常用的就是小波分析.Zhu 和Law[2]提出了一种基于小波分析的简支梁响应多尺度分解的裂纹识别方法,并通过仿真和实验进行了验证.在随后的研究中,为了检测多裂纹梁的识别效果,刘光耀等[3]利用小波分析与变异系数的结合,构建了新型检测指标,检测过程摆脱了对完好结构信息的依赖.Khorram 等[4]根据小波变换的局部极值,定义了一种移动荷载作用下的裂纹梁损伤指数,该指数可以检测到梁高10%以上的小裂纹.虽然理论上,小波分析可以分析非线性非平稳复杂信号[5],然而各种问题也在实际应用中出现,最突出的是小波分析的结果对初始基函数极为敏感.因此,初始基函数选择不同,将会带来巨大误差.对此,经验模态分解(EMD)[6]避免了小波变换的不足且得到了广泛使用.Meredith 等[7]通过对桥梁在车辆荷载作用下的加速度响应分析,验证了该方法可以检测出单损伤和多损伤.此外,以EMD 为基础的Hilbert-Huang 变换(HHT),广泛应用于工程信号处理.Roveri 和Carcaterra[8]研究了使用基于HHT 的方法对受损桥梁进行损伤检测的可行性,并在没有与未损坏结构的响应进行比较的情况下识别出了桥梁上的损伤位置.然而,EMD 没有严谨的理论基础,模态混叠、端点效应以及计算效率低等问题时常出现在应用过程中[9].虽然有很多学者针对EMD 的缺点进行了研究[10],但并没有从根本上解决.21 世纪初,变分模态分解(VMD)[11]在EMD 的基础上被提出,其原理不同于小波分析和Fourier 变换.VMD 保留了EMD 的优势,同时也克服了EMD 在迭代过程中出现的诸多问题.目前,VMD 在机械故障诊断中应用得最为广泛[12-14],但在土木工程领域应用甚少.Bagheri 等[15]分别应用人工神经网络和VMD,根据建立的模态频率与抗弯刚度之间的关系来确定桥梁的抗弯刚度.结果表明该方法能够在没有完整结构信息的情况下,预测桥梁的抗弯刚度.王超等[16]将VMD 和广义Morse 小波联合使用,得到了框架结构的瞬时频率.Mousavi 等[17]应用VMD 对受损桥梁的加速响应进行分解,并构造了新的损伤识别指标,成功地识别出了损伤存在的位置.据此,VMD 在桥梁损伤检测领域存在良好的应用前景.
本文提出的方法是一种不基于完整有限元模型的裂纹检测方法,且该方法仅需在跨中布置一个加速度传感器,减少了在实际工程中传感器的装卸以及维护工作.首先,本文推导出了在移动荷载作用下,带裂纹简支梁跨中位置处加速度的解析表达式.其次,在有限元模拟环境下,进一步建立了车轮荷载作用下的简支裂纹梁模型,并提取了跨中位置处的加速度响应.对加速度响应进行VMD,得到了含有损伤信息的模态,然后经过Hilbert变换得到了相应的瞬时频率和瞬时能量.同时,利用对损伤敏感的瞬时频率对裂纹存在的位置进行识别,可以识别出裂纹深度占比 δ在10%以下的小裂纹.构造了对裂纹深度敏感的指标来评估裂纹深度.最后,验证了该方法在不同的轮载大小、噪声程度以及裂纹数量条件下的有效性.
1 VMD


2 损伤指标的构建

3 移动荷载作用下裂纹梁动力分析
现如今,跨径在5 ∼20 m的小跨径桥梁中,简支板桥得到了广泛的应用.工程上,通常规定装配式板桥的跨径为 8 ∼16 m, 每块预制板的宽度在1 .0 ∼1.4 m 之 间,板厚约为 0.16 ∼0.36 m. 因此,假设梁长L=15 m,宽度B=1.2 m , 高度H=0.3 m.在移动荷载作用下,该类型桥梁的裂纹损伤识别可简化为如图1 所示的模型.

图1 移动荷载下的裂纹梁模型Fig. 1 A cracked beam model under a moving load



图3 给出了简支梁跨中位置处竖向位移响应的有限元模拟结果.为了便于结果的观察,模拟结果图的横坐标均采用了归一化的移动荷载位置x˜=x/L, 在匀速情况下,等于归一化时间t˜=t/T,下文均采用此方式.图3中的位移信号可以看作为两个正弦信号的叠加,高频部分在移动荷载达到裂纹位置处幅值有所增大.相位差在图中表现得不够明显,但其依然存在.所以,其结果基本符合上述理论推导.

图2 积分常数Fig. 2 Integration constants
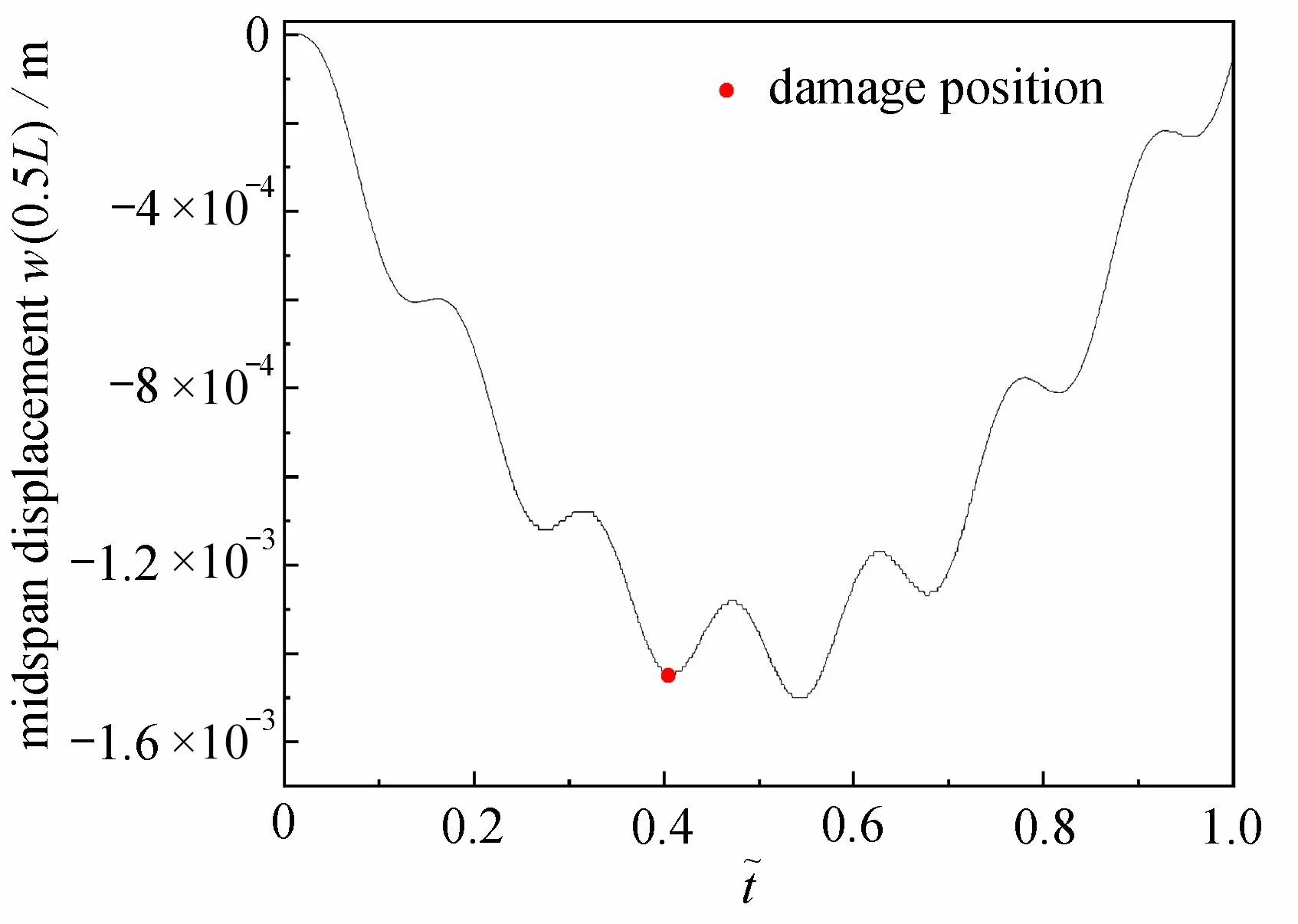
图3 跨中位移Fig. 3 The midspan displacement

有限元模拟的结果如图4 所示,跨中加速度响应可以认为是基频正弦部分和高频信息的叠加.同时,高频信息是由指数项(t)滋生的.由于高频信息的存在,图中不能很好地表现相位差,但其仍然存在.因此,其结果与推导结果基本吻合.由于裂纹的存在,导致移动荷载经过裂纹位置后,使其跨中加速度响应出现了幅值和相位的变化.本文所提出的方法正是利用了这些突变去识别裂纹损伤.

图4 跨中加速度Fig. 4 The midspan acceleration
4 数 值 算 例
事实上,车轮在路面运动过程中,与路面有一定的接触面积.为进一步贴切车轮作用在桥面的实际效果,本文将图5(a)所示的移动集中荷载P转换为图5(b)所示的非均布荷载.根据王扬[19]的研究,将该非均布荷载简化为二次抛物线的形式.一般车辆静态时,轮胎与路面的接触长度为r=10 ∼30 cm;由于车辆移动过程中,轮胎变形不充分,须进行一定的折减.本文取r=20 cm,且考虑折减系数为0.8,则实际接触长度为r×0.8=16 cm. 数值模拟的采样时间为1 2 s.其他相关参数均列于表1.
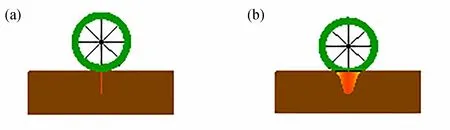
图5 车轮荷载:(a) 集中荷载;(b) 非均布荷载Fig. 5 The wheel load: (a) a concentrated load; (b) an ununiform load

表1 模拟工况Table 1 The simulation condition
4.1 损伤位置分析
对提取的跨中加速度信号进行VMD.VMD 方法的性能取决于输入参数,其中包括惩罚系数α、模态个数k等参数.本文取α =18 000,k=5,其他参数按照默认取值,即可满足工况一的需求.分解结果如图6 所示.
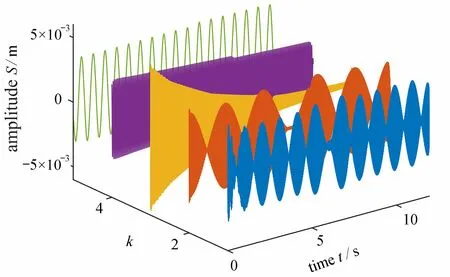
图6 VMDFig. 6 The VMD
由图6 可知,VMD 将加速度分解为5 个IMF 分量.在得到的瞬时频率中,发现IMF 4 分量的瞬时频率图能够准确地显示出工况1 的裂纹位置,结果示于图7.同时,当轮载通过裂纹位置后,可以看出瞬时频率幅值出现了一定的波动.由图8 可知,IMF 5 分量的瞬时能量波动范围的均值在裂纹位置处有明显的提升,且IMF 5 所对应的频率正是式(29)中的基频部分.根据这两种现象可知,VMD 将裂纹损伤带来的相位和幅值的突变,分别储存在了IMF 4 和IMF 5 两个分量中.然而根据式(29),裂纹损伤带来的相位和幅值的突变应该都在IMF 5 中,这可能受到了滋生高频部分的影响导致VMD 过程中出现了误差,致使相位突变包含到了IMF 4 中.相比于瞬时能量,瞬时频率对裂纹位置的识别更加准确.

图7 IMF 4 瞬时频率Fig. 7 The IMF 4 instantaneous frequency
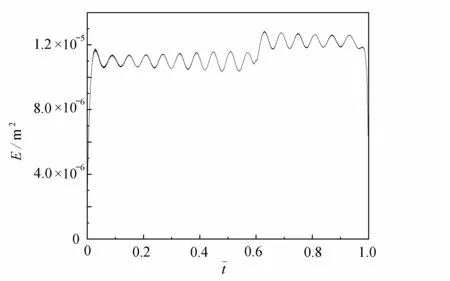
图8 IMF 5 瞬时能量Fig. 8 The IMF 5 instantaneous energy
4.2 损伤程度分析
研究人员对桥梁进行损伤检测时,一直都很关注检测手段能否对受损桥梁做出良好的损伤程度判断,这对桥梁剩余使用寿命的预测是非常关键的.本文对裂缝深度占比δ 分 别为 2 0%,1 5%,1 0%和 5%四种情况进行损伤程度的判断,其他条件与工况1 相同.其瞬时频率和瞬时能量图分别如图9、图10 所示.
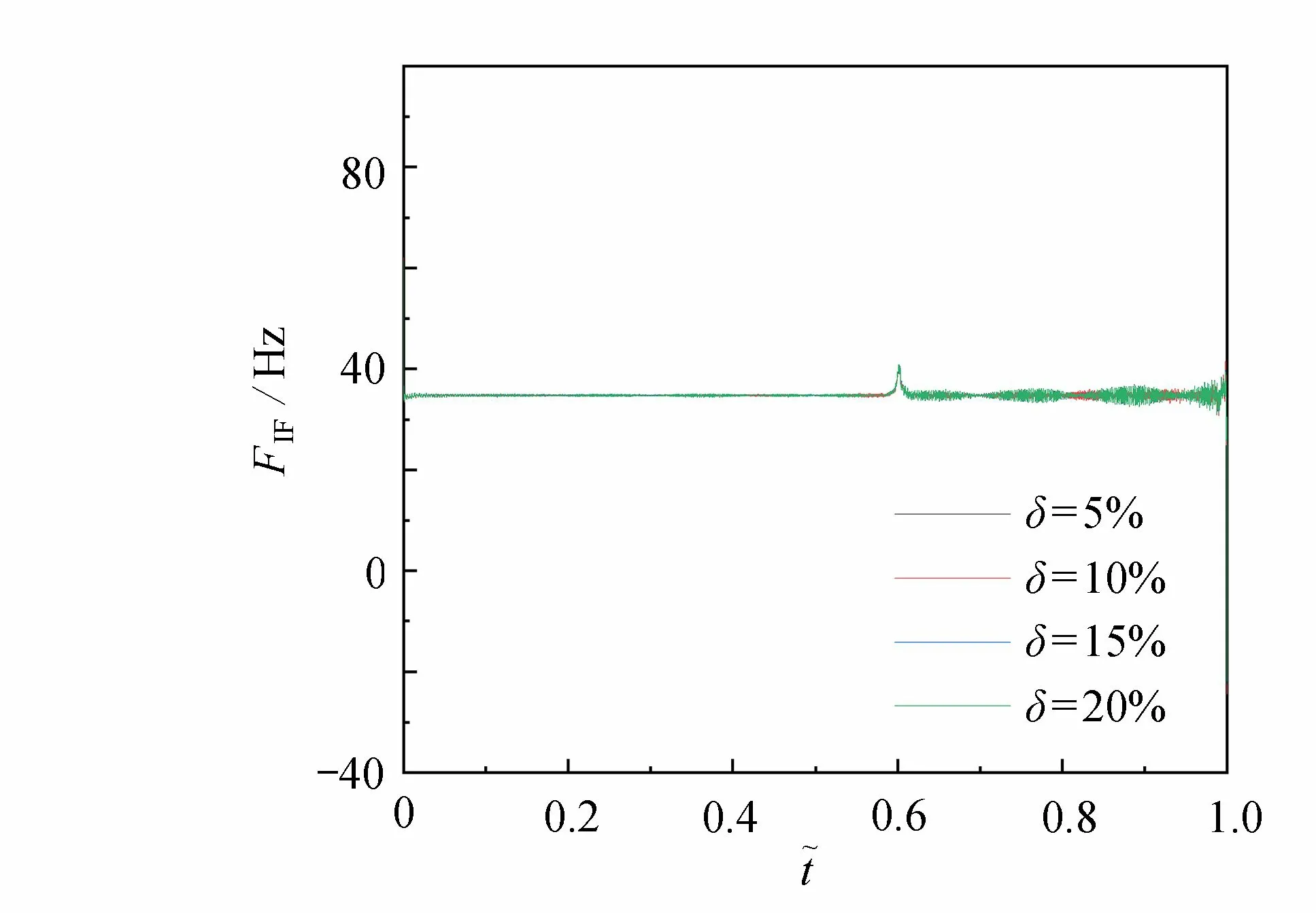
图9 δ 为 20 % ,15% ,1 0% ,5% 的瞬时频率对比Fig. 9 Comparison of instantaneous frequencies for δ= 20%, 15%, 10%, 5%

图10 δ为2 0% ,15% ,1 0% ,5% 的瞬时能量对比Fig. 10 Comparison of instantaneous energy for δ= 20%, 15%, 10%, 5%
从图9 中可以明显地看出,对于不同的裂缝深度,瞬时频率在裂纹位置处的峰值接近重叠,没有明显的区分度.轮载通过简支梁全过程的瞬时能量曲线示于图10.现取轮载未经过裂纹位置前的瞬时能量作为Ej,且Ej在 稳定范围波动(t˜ ∈(0.25,0.5)) ;取轮载经过裂纹位置后的瞬时能量均值Ei, 且Ei在稳定范围波动(t˜ ∈(0.65,0.9)) ,可求得均值能量差 ∆E.图11 给出了裂纹深度与 ∆E的关系图,可以清晰地看出,随着裂纹深度的增加, ∆E的值呈现出线性增加的趋势.由此可知, ∆E对损伤程度的大小有一定的敏感性.

图11 均值能量差Fig. 11 The mean energy difference
4.3 轮载大小影响分析
针对轮载大小对裂纹识别效果的影响,本文做了一定的分析.这里设置轮载大小分别为 5 kN,1 0 kN和15 kN三种情况,其他条件与工况1 相同,其瞬时能量示于图12.从图中可以看出,轮载大小的增加使得瞬时能量幅值也在不断增加.图13 给出了均值能量差 ∆E与轮载大小的关系.为选取合适的Ei和Ej,采取与4.2 小节相同的做法.可以看出, ∆E随着轮载大小的增加而逐渐增加.这也说明 ∆E可以区分不同轮载大小对检测结果的影响.
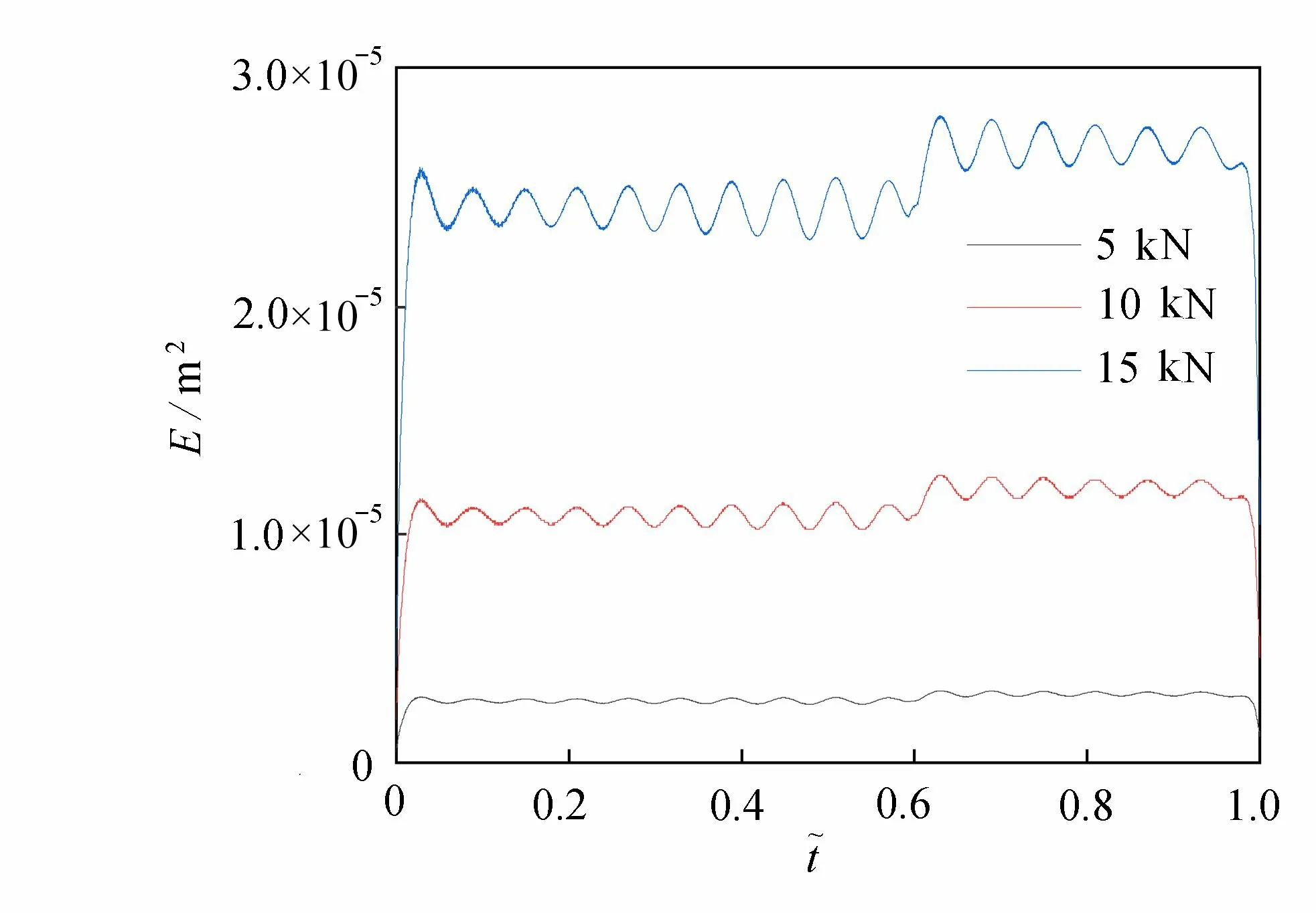
图12 三种轮载大小作用下瞬时能量对比Fig. 12 Comparison of instantaneous energies under 3 wheel loads

图13 均值能量差(轮载大小)Fig. 13 The mean energy difference (wheel load size)
4.4 双位置损伤分析
分别设置在6 m 和9 m 处存在裂纹损伤,并设置其裂缝高度占比 δ 分 别为 20%,1 5%,1 0%和 5%.在进行VMD 时,取α =9 000,其他参数不变.其瞬时频率示于图14.
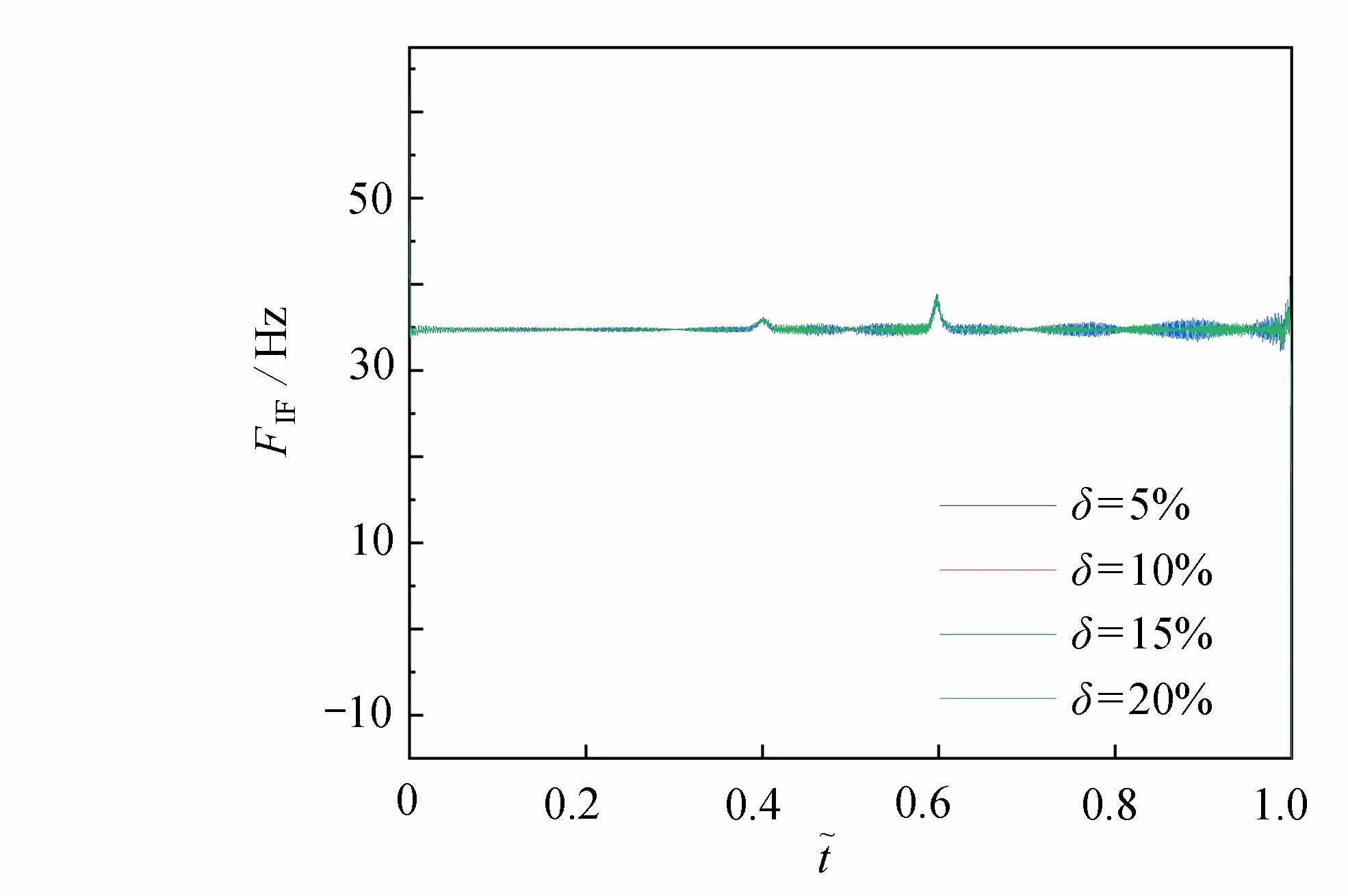
图14 δ 为 20 % ,15% ,1 0% ,5% 的瞬时频率对比(双位置)Fig. 14 Comparison of instantaneous frequencies for δ= 20%, 15%, 10%, 5% (2 positions)
从图14 可以看出,在6 m 和9 m 裂纹位置处,瞬时频率幅值都有一定的峰值突出,且位于右侧裂纹的瞬时频率峰值更加尖锐.然而,对于不同裂纹深度的区分,瞬时频率呈现的效果依然不佳.图15 给出了两处存在不同深度裂缝时的瞬时能量曲线.可以看出,瞬时能量波动范围的均值在6 m 和9 m 位置处都有所提升.由图16可知,在6 m 和9 m 位置处,随着裂纹深度的增加 ∆E的值大致呈现出线性递增的趋势.同时,Ei和Ej的选取与4.2 小节的做法基本相同.

图15 δ为2 0% ,15% ,1 0% , 5% 的瞬时能量对比(双位置)Fig. 15 Comparison of instantaneous energy for δ= 20%, 15%, 10%, 5% (2 positions)
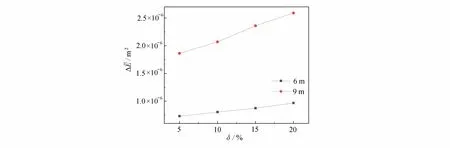
图16 均值能量差(双位置)Fig. 16 Mean energy differences (2 positions)
4.5 噪声影响分析
在实际的桥梁损伤检测中,环境噪声往往对识别结果有一定的影响.拥有良好的噪声鲁棒性,也是评判检测方法的重要因素.本文将三种不同程度的随机噪声添加到跨中加速度信号中,得到信噪比(SNR)分别为5 dB,1 0 dB和 1 5 dB的信号,其他条件与工况一相同.其瞬时频率分别如图17 ~ 19 所示.
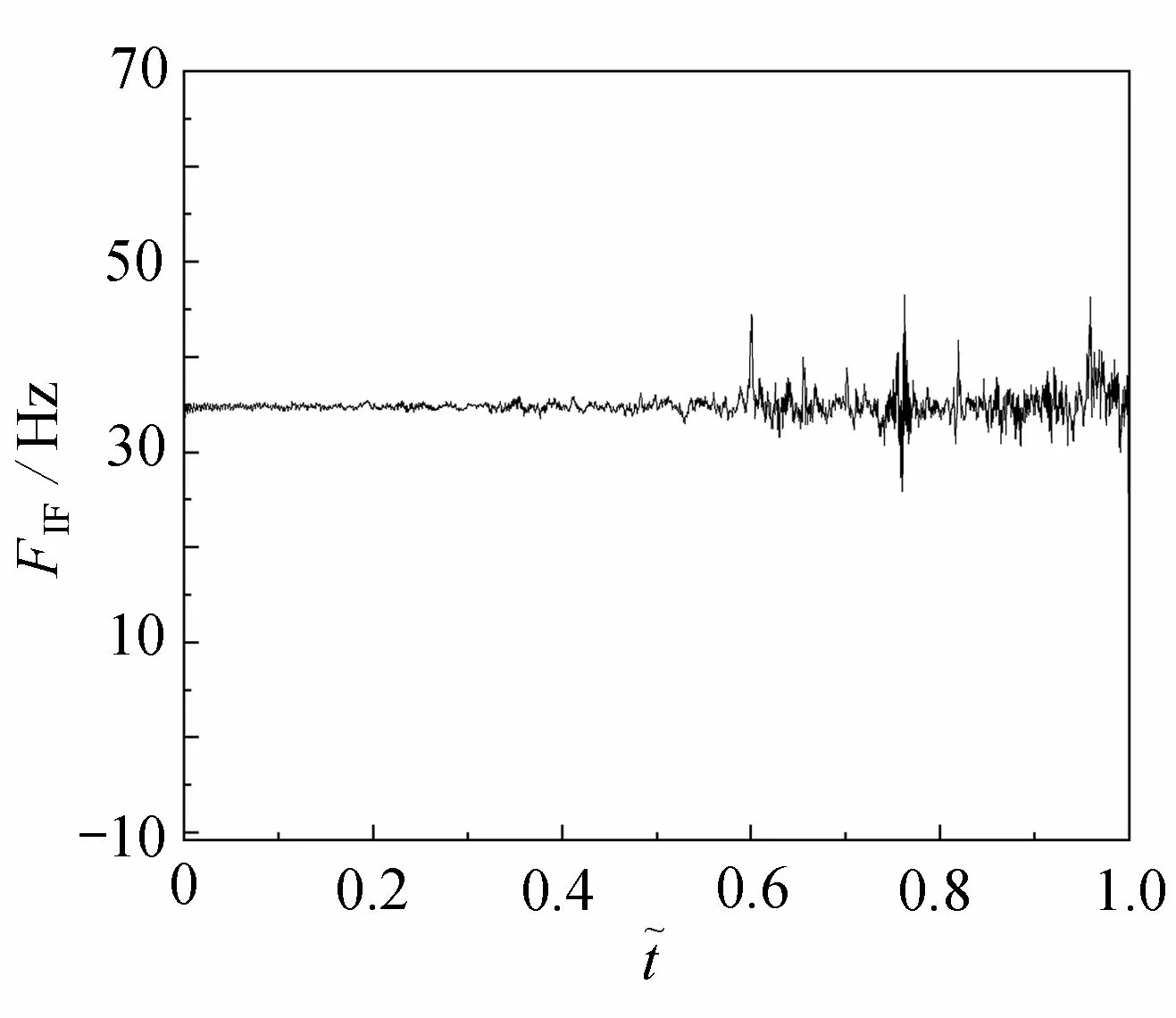
图17 信噪比为5 dBFig. 17 The SNR is 5 dB

图18 信噪比为10 dBFig. 18 The SNR is10 dB
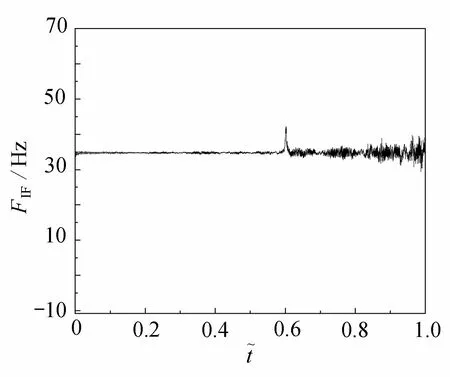
图19 信噪比为15 dBFig. 19 The SNR is 15 dB
从图中可以看出,当信噪比为5 dB时 ,9 m 处的裂纹位置很难识别;相较于信噪比5 dB, 在信噪比为1 0 dB的条件下,裂纹位置的识别效果较好,但是受到其他位置处瞬时频率波动的干扰;当信噪比为1 5 dB时,裂纹位置的识别仍具有良好的效果.所以基于VMD 分解的损伤识别方法具有一定的噪声鲁棒性.
5 结 论
本文根据振动理论推导出了带裂纹简支梁在移动荷载作用下的动态响应表达式,发现在移动荷载经过裂纹位置后,其跨中加速度响应出现了幅值和相位的变化,为数值模拟提供了理论支持.此外,采用有限元软件建立了符合规范的简支梁桥,并采用车轮荷载作用在桥面,提取其跨中加速度响应进行裂纹识别.可得到如下结论:
1) 加速度响应经过VMD 分解后,IMF 4 和IMF 5 分别包含了相位和幅值的突变,可以利用瞬时频率和瞬时能量进行体现;
2) 对于不同程度损伤的裂纹,甚至是深度占比为5%的小裂纹,瞬时频率都能够准确识别,但不能做到有效的区分,而均值能量差能够很好区分不同的裂纹深度带来的损伤;
3) 对双位置裂纹的识别,瞬时频率对裂纹位置的识别效果仍然可观,同时也可以利用均值能量差区分不同的裂纹损伤程度;
4) 在1 5 dB 信噪比的条件下,瞬时频率对裂纹位置的识别仍有良好的效果;
5) 该方法在不阻塞交通的前提下,仅需获取损伤桥梁跨中加速度响应即可进行裂纹识别,对实际工程应用具有参考价值.
然而,由于本研究的对象仅为简支梁桥这种常见桥型,对于其他类型的桥梁结构,该方法的实用性还需要进一步考证.
参考文献( References ) :
[1]ZHU J, ZHANG Y. Damage detection in bridge structures under moving vehicle loads using delay vector variance method[J].Journal of Performance of Constructed Facilities, 2019, 33(5): 4019049.
[2]ZHU X Q, LAW S S. Wavelet-based crack identification of bridge beam from operational deflection time history[J].International Journal of Solids and Structures, 2006, 43(7): 2299-2317.
[3] 刘光耀, 刘习军, 张素侠, 等. 基于小波分析和变异系数的简支梁桥损伤识别[J]. 应用力学学报, 2020, 37(5): 1915-1922. (LIU Guangyao, LIU Xijun, ZHANG Suxia, et al. Damage identification of simply supported beam bridge based on wavelet analysis and variation coefficient[J].Chinese Journal of Applied Mechanics, 2020, 37(5): 1915-1922.(in Chinese))
[4]KHORRAM A, BAKHTIARI-NEJAD F, REZAEIAN M. Comparison studies between two wavelet based crack detection methods of a beam subjected to a moving load[J].International Journal of Engineering Science, 2012,51: 204-215.
[5] 刘小靖, 周又和, 王记增. 小波方法及其力学应用研究进展[J]. 应用数学和力学, 2022, 43(1): 1-13. (LIU Xiaojing,ZHOU Youhe, WANG Jizeng. Research progresses of wavelet methods and their applications in mechanics[J].Applied Mathematics and Mechanics, 2022, 43(1): 1-13.(in Chinese))
[6]HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences, 1998, 454(1971): 903-995.
[7]MEREDITH J, GONZÁLEZ A, HESTER D. Empirical mode decomposition of the acceleration response of a prismatic beam subject to a moving load to identify multiple damage locations[J].Shock and Vibration, 2012,19(5): 845-856.
[8]ROVERI N, CARCATERRA A. Damage detection in structures under traveling loads by Hilbert-Huang transform[J].Mechanical Systems and Signal Processing, 2012, 28: 128-144.
[9] 孟宗, 季艳, 谷伟明, 等. 基于支持向量机和窗函数的DEMD端点效应抑制方法[J]. 计量学报, 2016, 37(2): 180-184.(MENG Zong, JI Yan, GU Weiming, at el. End effects restraining of DEMD based on support vector machine and window function[J].Acta Metrologica Sinica, 2016, 37(2): 180-184.(in Chinese))
[10] 邢昀, 荣剑. 常见不同模态信号分解方法探讨[J]. 现代计算机, 2018, 36: 7-11. (XING Yun, RONG Jian. Discussion on the signal decomposition methods of common modes[J].Modern Computer, 2018, 36: 7-11.(in Chinese))
[11]DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J].IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[12] 赵岩, 朱均超, 张宝峰, 等. 基于VMD与Hilbert谱的旋转机械碰摩故障诊断方法[J]. 振动、测试与诊断, 2018, 38(2):381-386. (ZHAO Yan, ZHU Junchao, ZHANG Baofeng, et al. Rub-impact fault diagnosis of rotating machinery based on VMD and Hilbert spectrum[J].Journal of Vibration,Measurement & Diagnosis, 2018, 38(2): 381-386.(in Chinese))
[13] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015,49(5): 73-81. (TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J].Journal of Xi’an Jiaotong University, 2015, 49(5):73-81.(in Chinese))
[14] 赵昕海, 张术臣, 李志深, 等. 基于VMD的故障特征信号提取方法[J]. 振动、测试与诊断, 2018, 38(1): 11-19.(ZHAO Xinhai, ZHANG Shuchen, LI Zhishen, et al. Application of new denoising method based on VMD in fault feature extraction[J].Journal of Vibration,Measurement & Diagnosis, 2018, 38(1): 11-19.(in Chinese))
[15]BAGHERI A, ALIPOUR M, OZBULUT O E, et al. Identification of flexural rigidity in bridges with limited structural information[J].Journal of Structural Engineering, 2018, 144(8): 4018126.
[16] 王超, 毛羚. 基于VMD和广义Morse小波的结构瞬时频率识别[J]. 振动、测试与诊断, 2020, 40(5): 957-962. (WANG Chao, MAO Ling. Instantaneous frequency identification of a structure using variational mode decomposition and generalized Morse wavelets[J].Journal of Vibration,Measurement & Diagnosis, 2020, 40(5) : 957-962.( in Chinese))
[17]MOUSAVI M, HOLLOWAY D, OLIVIER J C, et al. Beam damage detection using synchronisation of peaks in instantaneous frequency and amplitude of vibration data[J].Measurement, 2021, 168: 1-14.
[18]CHONDROS T G, DIMAROGONAS A D, YAO J. A continuous cracked beam vibration theory[J].Journal of Sound and Vibration, 1998, 215(1): 17-34.
[19] 王扬. 复杂轮胎力作用下沥青路面力学行为研究[D]. 博士学位论文. 北京: 北京交通大学, 2017. (WANG Yang.Study on mechanical behaviors of asphalt pavement under complicated tire force[D]. PhD Thesis. Beijing:Beijing Jiaotong University, 2017. (in Chinese))

