基于多参数协同耦合作用的熔融沉积填充速度优化控制研究

陈松茂 陈宇林 鲁忠臣

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

熔融沉积(Fused Deposition Modeling，FDM)增材制造技术具有设备成本低、维护简单、材料利用率高等优点，已被广泛应用于工业、医疗、教育等领域[1- 3]。然而，受到不可避免的台阶效应及材料性能等因素影响，FDM制件普遍存在成形精度不高或打印效率低等问题[4- 8]。对此，国内外学者开展了有关FDM工艺参数优化控制方面的研究来弥补以上不足[9- 15]。

部分研究发现，通过优化控制速度参数可有效改善制件的成型质量[16- 19]。Qin等[17]基于Hbot运动系统，提出了一种结合S型加减速函数模型的FDM实时自适应超前速度控制算法，通过减小加减速中的波动以及提升在连续角和曲线处速度控制的平滑程度，降低运动系统的不确定性和运动惯量，有效提高了FDM制件的尺寸精度、降低了表面粗糙度；Ertay等[18]提出了一种同步挤出与填充的速度控制方案，通过采用速度优化算法，获取时间采样位置数据和轨迹轮廓数据，同时考虑加热和挤出装置的限制、喷头驱动时的冲击、加速度和速度限制等因素，用于控制FDM打印机喷头的运动，有效改善了FDM制件在拐角与高曲率处的材料堆积问题，提高了产品的成型质量；Geng等[19]研究了填充速度与挤出速度对聚醚醚酮(Polyetheretherketone，PEEK)丝材的微观结构和尺寸精度的影响，研究发现，填充速度与挤出速度协调同步非常重要，决定了挤出丝材的尺寸，直接影响成形精度，需将速度与挤出丝直径的关系函数引入到速度控制算法中。而值得一提的是，由于制件往往存在不同大小的拐角，它们与速度之间的耦合也将影响相应位置处的精度，综合而言，速度与层厚、喷头温度和拐角等参数之间存在着联系。Brooks等[ 20]分析了不同直径大小的喷嘴在填充拐角轮廓时产生的成形精度误差对层厚、打印效率的影响，同时设计了一个具备内外层两级直径的喷嘴结构，兼顾了60°以内凸角轮廓的精度和打印效率；Woo等[21]在直接能量沉积过程(Directed Energy Deposition，DED)中应用拐角扫描速度控制算法和相关经验公式补偿扫描速度在拐角处的下降，控制矩形拐角处的过度沉积现象，使拐角处沉积高度与其他直线段等高且光滑，并使用多元回归分析了DED工艺参数和成型尺寸间的相关性。笔者前期研究也发现，填充速度与层厚、喷头温度以及制件的拐角等参数之间存在着交互耦合作用[22- 23]，通过相应的方差分析也证明了这种耦合作用的显著性，并且采用耦合函数计算获得的最优填充速度值进行FDM成型时，可以有效改善制件的成形精度，同时兼顾了打印效率。

前期研究中，并没有实现填充速度关于层厚、喷头温度和拐角的多元耦合，由于这些参数之间并非简单的二元交互耦合，而是多参数相互交织作用的。因此，文中在双变量打印实验基础上，进行了填充速度与层厚、喷头温度、轮廓拐角等多个参数协同耦合作用的优化控制方法研究，通过数据分析和多元非线性回归数学方法，构建了基于多参数协同耦合作用的填充速度优化控制函数，并结合误差分析、力学实验与断口微观形貌测量等手段，检验优化控制效果。

1 实验方案

1.1 打印实验

采用高诺A001打印机进行FDM打印(喷嘴孔径为φ0.4 mm)；实验材料为聚乳酸(Polylactic Acid，PLA)丝材(丝径φ(1.75±0.02) mm、熔点范围190～220 ℃)；精度测量仪器包括LF170锌合金电子数显卡尺(分辨率0.01 mm)、德国MDA2000数码显微镜(最高分辨率20万像素、最高倍率200倍)。

设计横截面形状及尺寸如图1所示的Ⅰ型(矩形)、Ⅱ型(方形)及拐角型(梯形)试样，厚度均为6 mm。其中：Ⅰ型和Ⅱ型试样主要用于研究填充速度与层厚、喷头温度的二元交互耦合关系，拐角型试样主要用于研究填充速度与轮廓拐角的二元交互耦合关系。

图1 各试样横截面形状及尺寸Fig.1 Shape type & size of each sample’s cross section

采用双变量打印实验方案，主要变量的取值如表1所示，其它工艺参数如表2所示。以等效尺寸偏差e作为Ⅰ型试样和Ⅱ型试样成形精度的评价指标(e值越小精度越高)，在α=90°的条件下，对Ⅰ型试样以vf和t为变量以及以vf和θ为变量进行共60组的打印[23]，对Ⅱ型试样也进行类似的实验；选取拐角轮廓的重复沉积区实际面积S1与漏沉积区实际面积S2之和(S1+S2)作为拐角试样成形精度评价指标(S1+S2的值越小，精度越高)，其测量方法如图2示，以vf和α为变量对拐角试样进行共30组的打印。每组实验均重复3次并取平均值，记录相关数据。

图2 拐角试样精度误差测量方法Fig.2 Accuracy error measuring method of contour corner samples

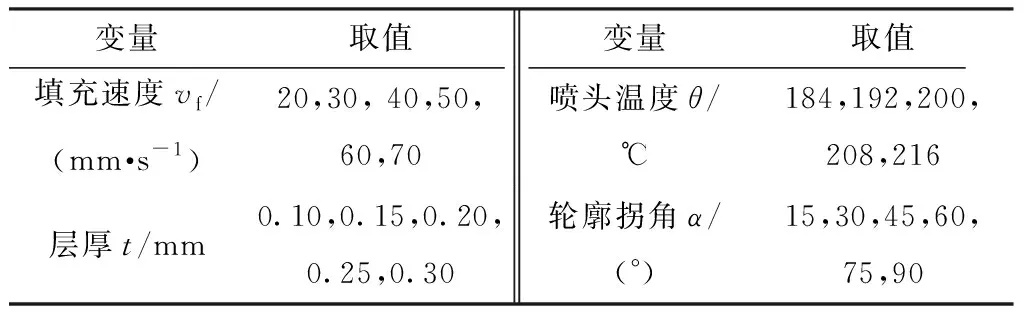
表1 主要变量取值Table 1 Value of main parameter variables

表2 其它工艺参数默认值Table 2 Default value of other process parameters.

1.2 力学实验

室温下，单向拉伸实验与弯曲实验均在AG-IC 50 kN型电子万能试验机上进行，实验速度均为5 mm/min。单向拉伸实验与弯曲实验的试样制备分别依据GB/T 1040—2006、GB/T 9341—2008进行，通过高诺A001 FDM设备打印获得。

1.3 形貌测量

采用德国Zeiss Supra 40场发射扫描电子显微镜(分辨率：1.0 nm @ 15 kV、1.9 nm @ 1 kV；放大倍数：12～1 000 000)，对单向拉伸实验断裂试样的断口微观形貌进行观察。

2 函数构建

2.1 数据统计

由打印实验可分别获得Ⅰ型、Ⅱ型、拐角试样对应的精度误差值。通过精度评价和对比后，统计在不同的参数组合情况下打印时获得最小e或S1+S2时对应的vf值(相对最优填充速度值)，结果如表3所示。此外，为了增加多元非线性回归数据样本、提高多参数协同耦合作用填充速度优化控制函数构建的准确性和可靠性，采用参数均布法则，增设如表4所示的8组参数组合，按照1.1节中打印实验方案分别进行Ⅰ型和Ⅱ型试样的打印，并统计对应的相对最优填充速度，结果如表5所示。

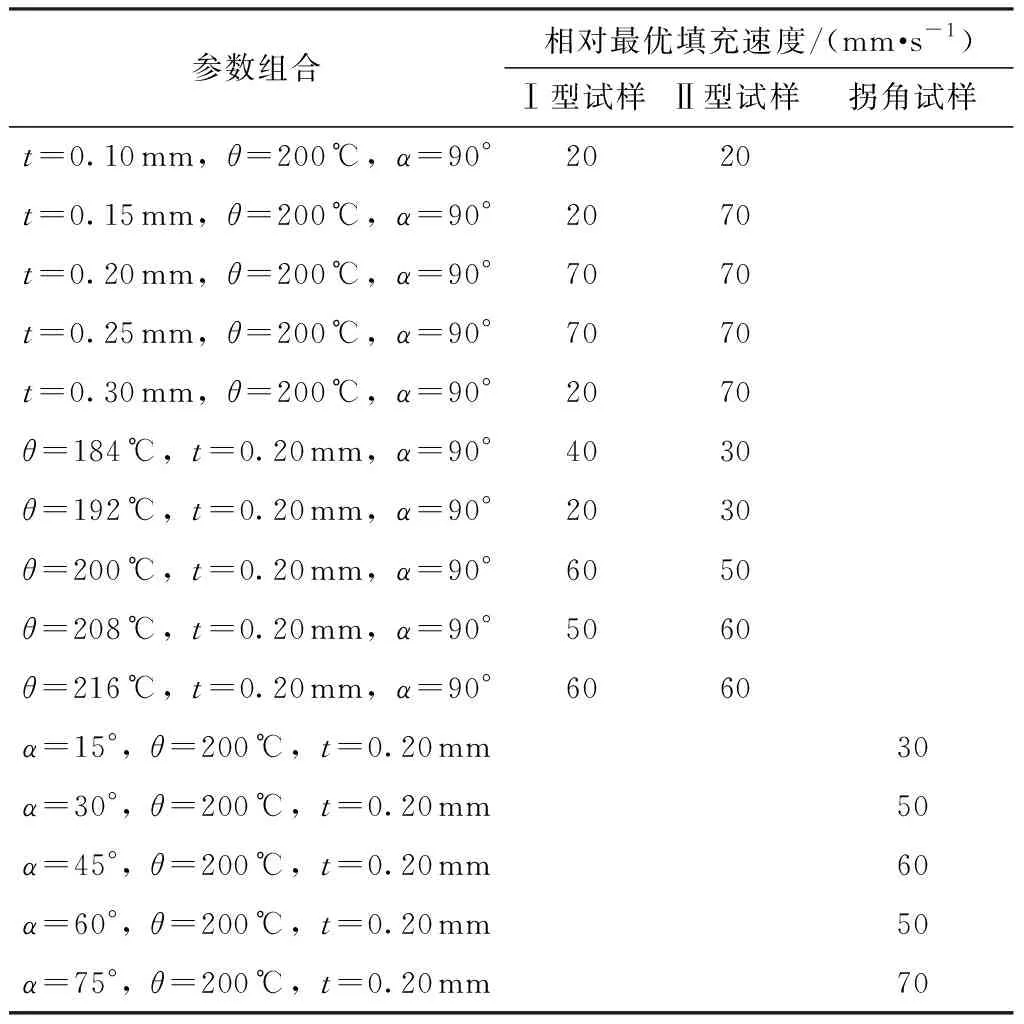
表3 相对最优填充速度值统计Table 3 Value statistics of relatively optimal filling speed

表4 增设的8种参数组合方式Table 4 Combinations of 8 additional parameters

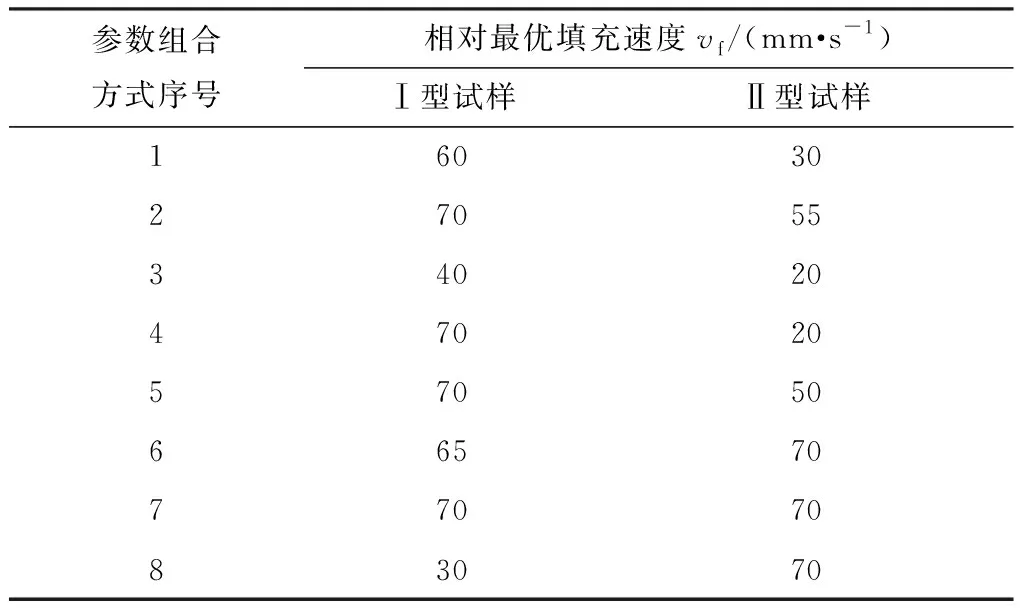
表5 表4中各参数组合方式对应的相对最优填充速度Table 5 Relative optimal filling speed corresponding to each parameter combination in Table 4

2.2 多元非线性回归函数构建

采用多元非线性回归数学方法，将填充速度vf视为响应值，t、θ和α视为影响因子，分别拟合

获得基于Ⅰ型&拐角型、Ⅱ型&拐角型的多参数协同耦合作用填充速度优化控制函数，如式(1)、(2)所示:

vf-Ⅰ=2 225.423 7+405.424 8t-23.130 3θ+

1.821 4α-1 071.895 4t2+0.059 2θ2-

0.015 2α2

(1)

vf-Ⅱ=-1 859.475 8+292.908 5t+18.398 5θ+

1.410 0α-590.604 6t2-0.046 0θ2-

0.010 1α2

(2)

3 成效检验

3.1 误差分析

表3、表5中的各参数组合对应的各类试样在相对最优填充速度值vf下将获得其相对最小精度误差值，这些误差值分布在不同的误差范围内，对之进行分布统计，如图3所示。

图3 最小精度误差值分布统计Fig.3 Distribution statistics of minimum accuracy error

由图3可知，Ⅰ型试样的最小精度误差值主要集中在0.26～0.35 mm之间，平均值为0.30 mm；Ⅱ型试样主要集中在0.11～0.30 mm之间，平均值为0.22 mm；拐角试样的最小精度误差值主要集中在0.16～0.45 mm2之间，平均值为0.44 mm2。同时，在这些试样的包括填充速度在内的已测试参数组合中，均可各筛选出使相应误差值最小的一组，这些组对应的参数组合即为该评价指标下的相对最优参数组合；但实际成型情况下由于评价指标、试样尺寸规格和形状特征等条件的不同，这种组合并不能完全适应各种要求；因此还是有必要研究在其他参数变化的情况下vf的相对变化情况并验证其效果。

根据前述准备工作，采用参数均布法，抽样打印表6所示的参数组合下成型的Ⅰ型试样、Ⅱ型试样和拐角型试样。其中：1-5组对应Ⅰ型试样，6-10组对应Ⅱ型试样，11-15组对应拐角型试样，Ⅰ型试样和拐角型试样的vf值采用式(1)计算获得，Ⅱ型试样的vf值由式(2)计算获得，其它工艺参数均采用表2所示的默认值。测量记录各参数组合对应的精度误差值和打印耗时，结果见表6。统计发现，各参数组合对应的精度误差值均低于或接近于前述最小精度误差平均值，具体而言，Ⅰ型试样的e平均值为0.25 mm，Ⅱ型试样的e平均值为0.15 mm，拐角型试样的平均S1+S2值为0.32 mm2。这些抽样结果中，平均e值减小了0.05 mm以上，平均S1+S2值减小了0.10 mm2以上，显然它们都低于优化前的平均值，且个别试样的误差值相比平均值降幅较为明显，这些数据表明：采用基于多参数协同耦合作用填充速度优化控制，试样的成形精度可以得到有效改善，且稳定可控。此外，打印耗时相对适中，在采用各vf值后，其耗时均能达到低速成型所耗时的75%以下，更接近高速成型的耗时，说明优化控制也在一定程度上兼顾了试样的成型效率。

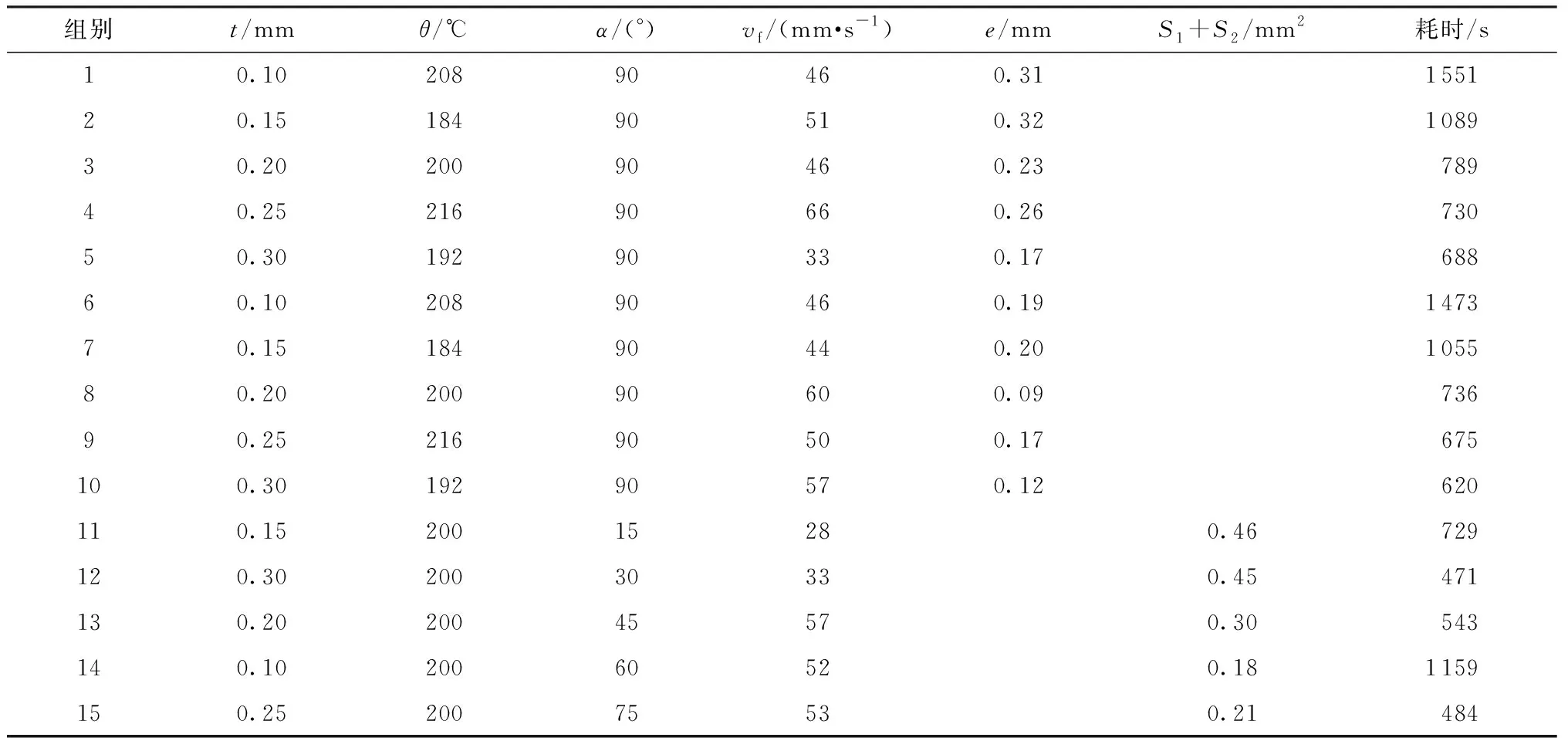
表6 抽样打印参数设置及结果统计Table 6 Parameter value & results of sampling printing

3.2 力学性能分析

以t=0.2 mm、θ=200 ℃的参数组合(其它工艺参数均采用表2所示的默认值)为例，分别选取vf=20 mm/s(低速)、vf=70 mm/s(高速)两组不采用优化控制的填充速度值和vf=46 mm/s(vf-Ⅰ函数计算)、vf=60 mm/s(vf-Ⅱ函数计算)两组优化后的速度值来成型单向拉伸实验与弯曲实验试样，并对它们进行拉伸或弯曲实验，每组实验均重复5次。实验结果如图4、图5和表7所示。其中，图4显示的是各参数组合对应实验序号是3的单向拉伸及弯曲实验中的应力-应变曲线；对应的最大应力折线图如图5所示。

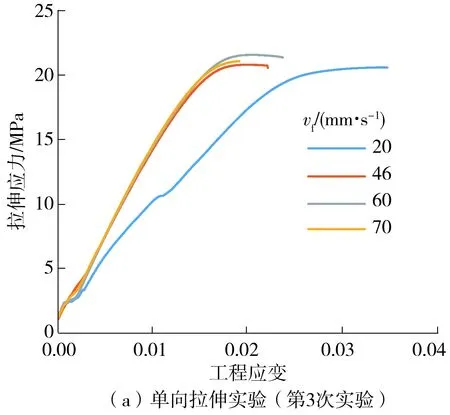
图4 不同试样的应力-应变曲线Fig.4 Stress-strain curves of different samples

由图4、图5及表7所示结果：在其它工艺参数相同条件下，各组试样的拉伸强度与弯曲强度差别不大；采用基于多参数协同耦合作用填充速度优弱试样抗拉能力，反而有所帮助；弯曲方面则是效果居中，其试样弯曲能力低于低速成型而高于高速成型的试样。出现这种现象的原因是，速度这一参数改变时对试样的力学性能影响并不大，更能造成影响的参数一般是填充率、外壳厚度等[24]。

图5 不同试样的最大应力值折线图Fig.5 Broken line graph of the maximum stress value of different samples

表7 不同填充速度下成型的试样的拉伸强度和弯曲强度Table 7 Tensile strength and flexural strength of samples formed at different filling speeds

3.3 断面形貌分析

抽取实验序号为3的单向拉伸实验断裂试样进行断面形貌观察，如图6所示。

图6 单向拉伸实验试样断面微观形貌Fig.6 Fracture morphology of uniaxial tensile samples

由图6可见，对试样的任一熔丝断面放大50倍后，熔丝的断面形状大多均为跑道形，且在它们交错的地方形变量最大，同时也正是这些地方构成了试样的基本力学强度，4组试样断面的熔丝交错黏合清晰可见，丝径及形变大致相同，层与层间熔丝粘结度差异不明显，也因此表现出相对接近的力学性能。放大5 000倍后发现：vf=20 mm/s的熔丝断面较为平整，这说明试样受到拉伸时熔丝之间的相互作用力与那些稍微不平整的断面对比会稍微小一些，表现出较强的脆性特征，这表明其拉伸性能稍差(这与单向拉伸实验相吻合)，而且断面存在的若干微小孔隙缺陷也是降低其拉伸强度的要素之一；vf=46，60 mm/s时熔丝断面特征分别是较不平整但有孔隙、较平整但无孔隙，也因此表现出稍好的拉伸性能；但vf=70 mm/s时断面则存在较多的细小拉丝缺陷和孔隙。以上分析是从微观形貌特征的角度出发的，结合力学部分的数据共同验证了在相同工艺参数条件下，采用基于多参数协同耦合作用的填充速度优化控制，可以打印出具有相对较佳拉伸性能的制件。

4 结论

(1)熔融沉积填充速度与层厚、喷头温度、轮廓拐角等参数存在交互耦合作用关系。利用双变量打印实验，分析获得填充速度与层厚、喷头温度、轮廓拐角二元交互耦合作用时的相对最优数值，并结合多元非线性回归方法，可构建基于多参数协同耦合作用填充速度优化控制函数。

(2)最小精度误差分析和抽样打印实验结果表明，采用基于多参数协同耦合作用优化控制函数计算获得的填充速度值进行打印，试样的精度误差值均低于或接近于最小精度误差平均值，抽样结果中，平均等效尺寸偏差减小了0.05 mm以上，平均拐角误差减小了0.10 mm2以上，且打印耗时小于该条件下最大耗时的75%，这些数据表明优化控制填充速度可有效改善成形精度，并且兼顾打印效率。

(3)力学实验结果和断面微观形貌特征表明：在其它工艺参数相同条件下，采用基于多参数协同耦合作用填充速度优化控制，可以小幅提升制件的抗拉性能。