高压辊磨机辊轴的有限元分析与疲劳评估

王 岩，刘 洋，杨柳松

1洛阳矿山机械工程设计研究院有限责任公司 河南洛阳 471039

2矿山重型装备国家重点实验室 河南洛阳 471039

高 压辊磨机是近年来在水泥用辊压机基础上研发的新型粉磨设备，具有生产能力大、破碎比大、节能显著及维修方便等优点[1]。高压辊磨机主要由机架、挤压辊、传动装置和进料装置等部件组成。挤压辊主要由辊轴和辊套组成。辊轴在轴向上具有变截面的特点，在截面变化处采用圆角和台阶过渡，在挤压载荷的作用下，往往由于应力集中而发生疲劳断裂[2]。

采用有限元分析方法对辊轴整体应力分布和位移情况进行精确地计算，具有快速、准确、方便的优点。笔者查阅资料发现，以往对辊轴的有限元分析中存在诸多问题，例如建模与实际情况相差较大、结构特征处理过于简化、网格划分粗糙以及过约束等，从而造成分析结果不够精确，设计指导性不强。

针对以上问题，笔者以 GM200-120 高压辊磨机为研究对象，运用有限元分析方法和疲劳强度评估方法对辊轴进行仿真分析和疲劳评估。

1 高压辊磨机工作原理

高压辊磨机挤压辊由活动挤压辊和固定挤压辊组成，两辊直径相同、轴线相互平行且彼此有一定间隙[3]，工作原理如图 1 所示。高压辊磨机启动电动机后，在电动机的驱动下辊轴开始转动，同时活动辊受到液压缸持续的推力挤压物料，物料挤压产生反作用力作用在固定辊上，2 个挤压辊以相同速度、相反方向转动。当物料从给料口落入到 2 个挤压辊之间时，受到 2 辊的碾压破碎并挤压成密实的料饼而排出。

图1 高压辊磨机工作原理Fig.1 Working principle of high-pressure grinding roll

2 物料挤压分析

高压辊磨机工作时，挤压辊受到的载荷有料层挤压力、电动机转矩、辊轴端部减速器产生的弯矩和重力等，其中料层反作用力在整个模型中是主要的作用力[4]，决定着辊轴的整体应力水平。在不影响计算精度的前提下，忽略重力、转矩、弯矩等的影响，辊轴可视作受到纯弯曲作用的简支梁，其受到的载荷即物料的挤压力。

挤压力的大小与作用在辊套表面的推力相平衡，因此根据液压缸压力计算得到的总推力可近似视为挤压辊受到的总挤压力。挤压力载荷的分布与物料的破碎过程相关。高压辊磨机物料破碎为层压粉碎，其粉碎过程可分为 3 个区域：加速区、压缩区和反弹区，以A1A2、B1B2、C1C2、D1D2平面作为分界面。根据物料挤压过程的粉碎机理，挤压辊表面只在压缩区和反弹区受力，以铁矿石为例，计算得到的圆心角为-2°～6°[5]。

3 建立有限元模型

3.1 建立几何装配模型

辊轴结构如图 2 所示。以往对辊轴的有限元分析中只包含辊轴和辊套，忽视了结构中与辊轴存在装配关系的其他构件。为了验证不同的装配模型对计算结果的影响，笔者建立了 2 种辊轴分析模型，以下称为模型 A 和模型 B，涵盖的零件范围如表 1 所列。

图2 辊轴结构Fig.2 Structure of roll

表1 2 种辊轴模型Tab.1 Two assembly models of roll

对辊轴的有限元分析中一般不包含轴承，分析者通常将轴承约束直接加载在辊轴对应轴承面上，这与实际情况不符，直接影响辊轴的应力计算结果。笔者将轴承内圈纳入到分析模型中，目的是为了确保约束条件与实际情况保持一致。

在装配模型中，装配面的结构特征和细节对构件局部的应力计算有很大的影响，因此对模型中各构件的圆角、倒角等细节特征均予以保留，仅对螺栓孔等无关的特征进行简化处理，以方便网格划分。

挤压辊整体在轴向上沿中心基本对称，为了确保高的模型精度，节约计算资源，选取辊轴一端作为计算模型，将三维装配模型导入到有限元分析软件MSC Patran 中进行非线性静力学分析。

3.2 网格划分

网格划分是建立有限元模型的一个重要环节，所划分的网格形式对计算精度和计算规模将产生直接影响。笔者根据有限元网格划分原则，为了确保得到连续性好的云图以及稳定的应力结果，采用精度更高的六面体单元对模型进行划分，对应力集中部位切分区域并采用密网格划分，对辊轴中心段等计算数据变化梯度不大的部位采用疏网格划分，网格整体疏密合理过渡。辊轴网格划分如图 3 所示，以模型 A 为例共得到 920 002 节点和 840 002 个单元。

图3 辊轴网格划分Fig.3 Mesh generation of roll

3.3 边界条件设置

模型对称剖面施加轴向对称约束。挤压辊采用向心轴承，施加约束时，可仅对轴承中心径向方向的自由度进行约束，以与实际工作时产生的自由度相吻合。由此，模型 3 个方向的自由度均被约束，既不会发生整体的刚性位移，也不会产生过约束导致不正确的计算结果。

辊轴与辊套、辊轴与轴承之间为过盈装配关系。此次分析不考虑过盈装配的影响，简化为绑定接触，轴套 1、轴套 2 与辊轴、轴承均设置为接触关系，摩擦因数设置为 0.1。

根据液压缸工作压力，计算总挤压力为 9 000 kN，加载在辊套表面圆心角 -2°～6°范围内。

以模型 B 为例，图 4 显示了施加的载荷和约束情况。

图4 模型 B 边界条件Fig.4 Boundary conditions of model B

3.4 材料参数设置

设置各构件的材料属性后提交求解计算。辊轴采用实测数值，弹性模量E=210 GPa，泊松比μ=0.27，屈服强度σs=625 MPa，抗拉强度σb=830 MPa。

4 有限元分析

4.1 辊轴位移分布

辊轴应首先保证位移在合理的范围内，辊轴位移分布云图如图 5 所示。在挤压载荷下，辊轴以轴承中心为支点发生弯曲变形，辊轴中间段的位移最大，模型 A 的最大位移为 0.205 mm，模型 B 的最大位移为0.199 mm。2 个模型的位移略有变化，说明模型装配范围对仿真计算是有影响的。由图 5 可以看出，辊轴具有足够的刚度。

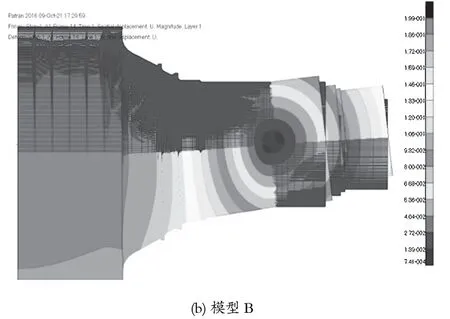
图5 辊轴位移分布云图Fig.5 Displacement contours of roll

4.2 辊轴应力分布

辊轴等效应力分布云图如图 6 所示。辊轴应力集中区域与预测一致，各凸台根部的圆角区域应力明显大于其他部位。模型 A 的等效应力最大值为 77.3 MPa，位于第 1 个凸台根部的圆角位置；模型 B 的等效应力最大值为 93.1 MPa，位于第 1 个凸台右侧面与轴套 1 相接触的边沿，系由轴套 1 对凸台挤压造成。

图6 辊轴等效应力分布云图Fig.6 Equivalent stress contours of roll

由纯弯曲梁受力情况可知，当弯曲曲率为正时，中性层之上为压应力，中性层之下为拉应力，有限元分析结果显示辊轴的最大和最小主应力云图完全符合这一特征，如图 7、8 所示。模型 B 纳入的装配构件轴套 1 和轴套 2，在辊轴受载弯曲时由于辊轴第 1 个凸台参与受力，抵抗了部分弯曲变形，由此导致了辊轴的位移略有降低。

图7 辊轴最大主应力分布云图Fig.7 Maximum principal stress contours of roll

图8 辊轴最小主应力分布云图Fig.8 Minimum principal stress contours of roll

5 辊轴疲劳强度评估

国内外企业广泛使用疲劳极限理论[6]推导辊轴的疲劳极限值，然后根据有限元计算结果对辊轴的疲劳性能进行评估。该计算方法(即 Shigley's 理论计算法)依据构件材料的抗拉强度，综合构件的表面状态、截面尺寸、载荷类型、温度变化和可靠度等因素，推导出实际构件的疲劳极限值。经计算，当可靠度取 99%时，辊轴无限寿命(循环次数N=107)的疲劳极限值为 85.4 MPa。

根据有限元分析结果，提取辊轴应力集中部位(见图 9)的最大和最小主应力，如表 2、3 所列。考虑到平均应力的影响，用古德曼方程对应力幅进行修正，得到修正应力幅。如果修正应力幅小于辊轴疲劳极限值，则辊轴的设计满足疲劳强度要求。对表中数据分析可知，模型 A 由于是自由弯曲，拉应力和压应力的大小基本一致；模型 B 由于轴套有抵抗弯曲变形的作用，因此压应力最大值由圆角 2 移动到圆角 3，使圆角 2 的应力幅降低，辊轴各部位的疲劳强度均能够满足疲劳极限的要求。

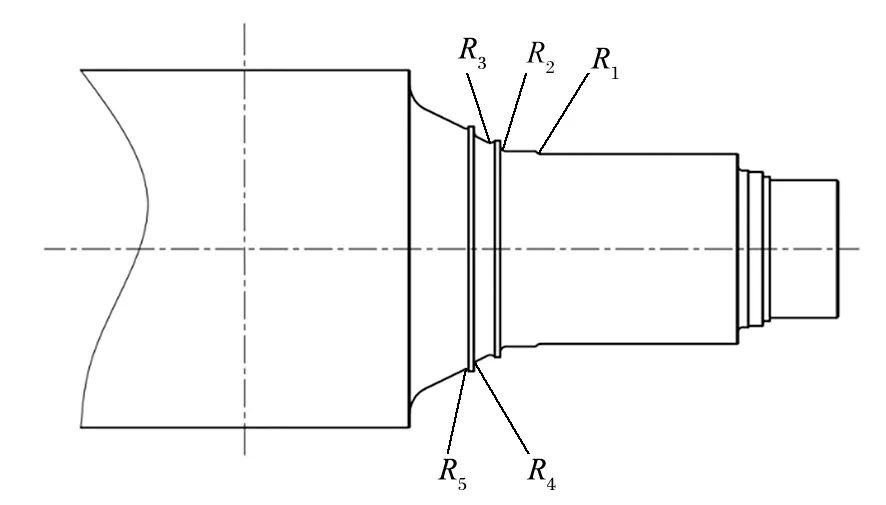
图9 辊轴应力集中部位Fig.9 Stress concentration position of roll

表2 模型 A 疲劳强度评估Tab.2 Fatigue strength evaluation for model A

表3 模型 B 疲劳强度评估Tab.3 Fatigue strength evaluation for model B

6 结语

(1)通过建立 2 种高压辊磨机辊轴的装配模型，运用有限元处理方法对模型进行处理，包括对模型细节特征予以最大保留、合理的网格划分、确定载荷及加载范围、施加约束条件，以及对辊轴物理参数和性能指标进行实测，确保有限元分析结果的准确性。

(2)运用 Shigley's 理论，计算得到辊轴无限寿命的疲劳极限值，将有限元计算结果修正后与疲劳极限值对比。结果表明，建立正确的装配模型可以得到更加准确的位移和应力分布结果。根据仿真分析及疲劳评估结果，辊轴的设计满足刚度、强度和疲劳性能的要求。