不同极化模式的二维大地电磁非线性共轭梯度反演及应用研究

徐凤姣,谢兴兵,郭全仕

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.中国地质大学地球物理与空间信息学院,湖北武汉430074;3.长江大学油气资源与勘探技术教育部重点实验室,湖北武汉430100)

随着大地电磁(MT)正演精度的不断提升,大地电磁反演与实际资料处理解释能力也获得了较大提高,并已应用于油气、地热田及矿产资源勘探等实际地质解释[1-6]。由于大地电磁反演的目标函数与模型参数之间存在极强的非线性,开展大地电磁非线性反演方法研究意义重大。目前,常用的大地电磁非线性反演方法主要有快速松弛反演(RRI)、Occam反演、Gauss-Newton(GN)反演和非线性共轭梯度(NLCG)反演等[7-11]。其中,非线性共轭梯度法因其具有稳定性强、收敛速度快的优势,目前已成为大地电磁实际资料处理中最重要的二维反演方法之一[10]。该方法基于FLETCHER等[12]提出的共轭梯度法,在计算过程中避免了直接计算Jacobin矩阵,取而代之的是求解矩阵与向量的乘积,并在共扼梯度方向模型空间里寻找一个使目标函数取得极小值的解。2001年,RODI等[10]在进行大地电磁数据二维反演时,将非线性共轭梯度方法引入计算,得到了较好的应用效果。ZHDANOV[13]将非线性共轭梯度方法应用于电磁偏移成像中,对比可知,该方法的计算效率是普通牛顿算法的N/2倍(N为网格剖分节点数)。余年等[14]将Occam反演结果作为非线性共轭梯度反演的初始模型,开展南涪线梓里隧道的大地电磁资料处理解释,反演结果与地质构造具有较高的一致性。2014年,相鹏[15]提出一种改进的预条件非线性共轭梯度反演算法,通过构建性状更接近于Gauss-Newton海森矩阵的预条件算子,提高了反演精度及效率。同年,赵维俊等[16]采用非线性共轭梯度反演方法,开展内蒙古扎鲁特盆地大地电磁实际资料处理解释,对比电阻率TE模式、TM模式以及TE+TM模式反演结果发现,TE+TM模式的反演结果能更好地拟合地下构造。2017年,刘才华[17]基于非线性共轭梯度反演方法,在嫩江县多宝山矿区开展大地电磁野外资料处理解释,为潜在成矿区精细勘探提供了有效靶区。2019年,韩江涛等[18]通过对长周期大地电磁资料进行非线性共轭梯度反演,揭示了复杂多重构造体系下软流圈的分布特征。近年来,大地电磁勘探方法在资源勘查领域取得良好勘探效果,主要源于非线性共轭梯度反演方法的改进与突破。

二连盆地朝克乌拉凹陷勘探程度较低,前期主要开展过1∶200 000重磁勘探,少量二维地震勘探,并在朝4洼陷中钻了一口探井。经过前期勘探,凹陷内的基底埋深及储层(白垩系低阻层)空间展布仍不清楚,需要对凹陷进行整体评价。基于此,在朝克乌拉凹陷朝4洼陷中布设了一条大地电磁测线,进行资料的处理、反演与解释。本文首先进行了非线性共轭梯度二维大地电磁反演方法研究;其次,进行反演算法模型测试;最后,基于上述反演方法研究与模型测试的认识,开展朝克乌拉凹陷大地电磁实测资料的处理与二维反演,并进行了综合解释。

1 方法原理

地球物理反演是通过地表实测数据求取地下真实地质模型的过程,本质上属于数学问题。在实际反演过程中,无法找到非常精确的模型来完全拟合实际数据,一般是通过迭代反演模型,使计算正演响应与实际数据之间的拟合差达到设定的最小值,从而尽可能使模型响应逼近观测数据。通常定义一个目标函数来度量模型响应与观测数据之间的差异,即:

ε=d-F(m)

(1)

式中:ε为拟合误差;d=(d1,d2,…,dn)T为观测数据向量;F(·)为正演算子;m=(m1,m2,…,mM)T为模型向量。

在实际地球物理反演过程中,仅仅将实测数据与正演结果进行拟合,会出现反演结果的多解性。为降低解的多解性,TIKHONOV等[19]提出一种正则化准则,即在目标函数中引入模型变量,通过同时约束数据变量与模型变量,使得目标函数取极小值。目标函数为:

(2)

式中:m0为初始模型向量;λ为正则化因子(大于0);Cd为数据方差矩阵;Cm为模型方差矩阵。

本文采用非线性共轭梯度算法开展大地电磁反演研究,将目标函数定义为:

(3)

式中:mref为参考模型向量;d为实际数据向量。

依据NEWMAN等[20]对非线性共轭梯度算法流程的研究,具体实现步骤如下:

3)搜索最优步长αi,使得V(mi+αiui)取最小值;

4)令mi+1=mi+αiui,ri+1=-V(mi+1);

6)取i=i+1,跳转到步骤3),直到满足收敛条件,反演结束。

在上述算法中,我们需要计算目标函数的负梯度来得到共轭梯度,并在该方向上搜索一个步长以得到目标函数的极小值,再以该极值点作为新的模型,计算下一个共轭梯度方法的极小值点,最终达到收敛条件,结束反演。在非线性共轭梯度迭代过程中,目标函数梯度的表达式为:

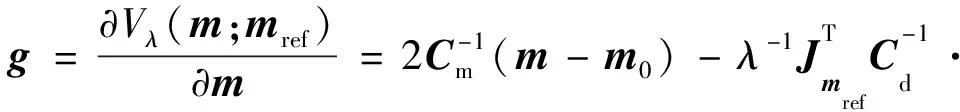
[d-F(mref)-Jmref(m-mref)]

(4)

式中:Jmref=∂F(·)/∂m为灵敏度矩阵。

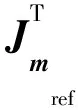
2 模型测试

分别采用TE、TM、TE+TM的极化模式开展不同模型条件下大地电磁非线性共轭梯度二维反演模型测试,以验证不同反演方法对地下复杂构造的适用性与有效性。TE极化模式采用ρTE视电阻率和φTE相位资料进行反演计算,TM极化模式同样采用ρTM视电阻率和φTM相位资料进行反演计算,而TE+TM的极化模式采用ρTE+TM=(ρTE+ρTM)/2视电阻率和φTE+TM=(φTE+φTM)/2相位资料进行反演计算,其中相位φTE和φTM需要旋转到第一象限再计算。

2.1 模型一:块体低阻模型

如图1所示,在电阻率为100 Ω·m的均匀半空间中,设置一个大小为4 km×4 km,埋深为5 km,电阻率为10 Ω·m的低阻异常体。地表布设1条30 km的测线,点距为0.5 km,共61个测点。在10-3～103Hz频率范围内,按其常用对数等间距设置61个频点,最小网格大小为1 km×1 km。

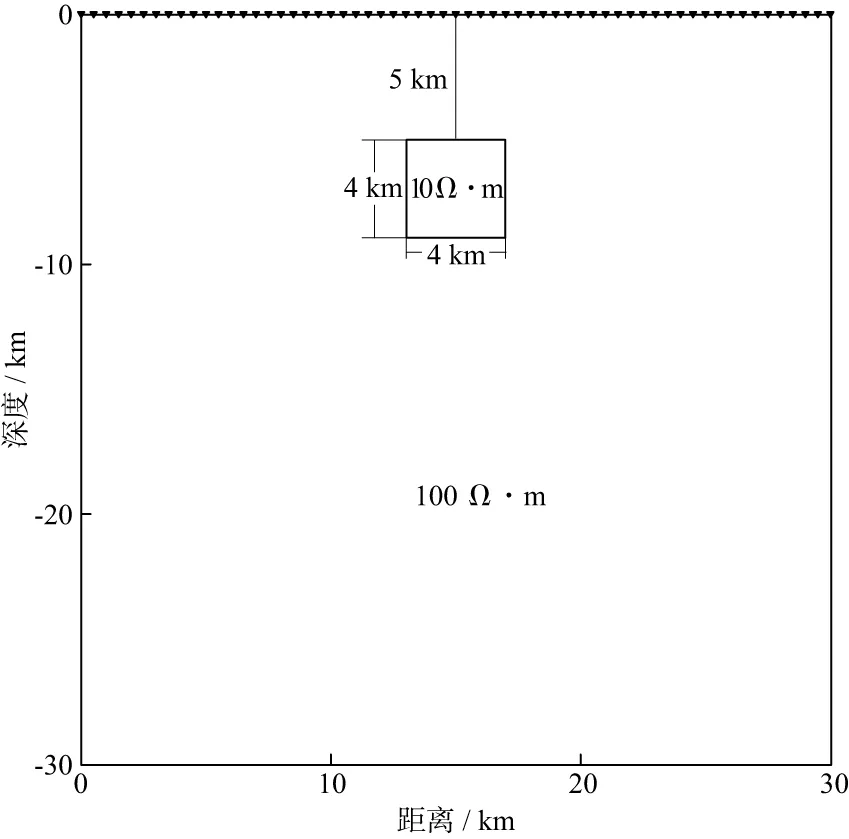
图1 块体低阻模型

本次反演计算在主频为2.50 GHz、内存为4G的Intel(R)Core(TM)i5-7 200U处理器PC机上运行。在正演数据中加入了5%的高斯随机噪声,作为反演观测数据,以50 Ω·m均匀半空间作为初始模型,开展非线性共轭梯度反演计算。经过30次迭代计算,得到如图2所示的反演结果。图2a、图2b和图2c分别为TE、TM、TE+TM极化模式的反演结果,可以看出,异常体的位置与理论模型具有较高的一致性,说明采用非线性共轭梯度算法开展大地电磁二维反演具有可能性和有效性,其中,TE+TM极化模式对异常体位置的刻画优于TE模式和TM模式。图2d为TE、TM和TE+TM极化模式条件下拟合误差随迭代次数的变化曲线,可以看出,当迭代次数达到30次时,这3种极化模式条件下反演误差趋于不变,但TE+TM模式前期收敛速度较快,且后期拟合精度更高。

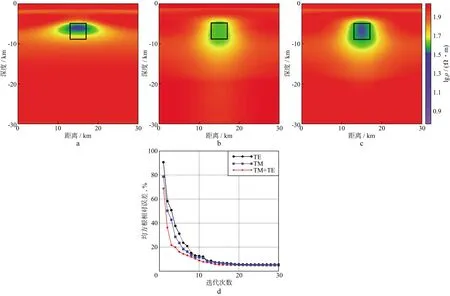
图2 块体低阻模型不同极化模式的反演结果

2.2 模型二:隐伏构造模型

为测试非线性共轭梯度反演方法对地下复杂隐伏构造的适用性,我们设计了如图3所示的隐伏断层、地垒和地堑模型,开展TE、TM、TE+TM极化模式反演研究。模型均为沉积地层模型,电阻率从地表到深部依次为高阻—低阻—次高阻分布。设置观测点个数为101个,点距为0.2 km,频点数为38个,频率范围为0.001～320.000 Hz。

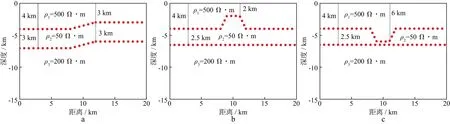
图3 隐伏构造模型

以100 Ω·m的均匀半空间作为初始模型,开展隐伏构造模型非线性共轭梯度反演计算,每个模型计算耗时约10 min,获得如图4所示的反演结果。图4a 从左至右分别为TE、TM、TE+TM极化模式经过30次迭代的断层模型反演结果,反演均方根误差分别为5.27%,6.38%,4.29%,对断层模型边界的刻画均较好。图4b从左至右分别为TE、TM、TE+TM极化模式经过30次迭代的地垒模型反演结果,最终均方根误差分别为6.39%,6.02%,6.18%,可以看出,反演结果中凸起边界的收敛效果低于层状界面,基本能刻画出二维层状地层中的地垒模型。图4c 从左至右分别为TE、TM、TE+TM极化模式经过30次迭代的地堑模型反演结果,其均方根误差分别为6.12%,5.57%,5.68%,地堑模型凹陷区边界收敛效果也低于层状界面,可能是由于地形突变,模型网格剖分精度不够引起,但总体反演效果较好。对比不同模型和不同极化模式的反演结果可以看出,基于TE+TM极化模式的反演电阻率剖面,对模型边界的刻画和物性的收敛效果优于TE、TM极化模式。

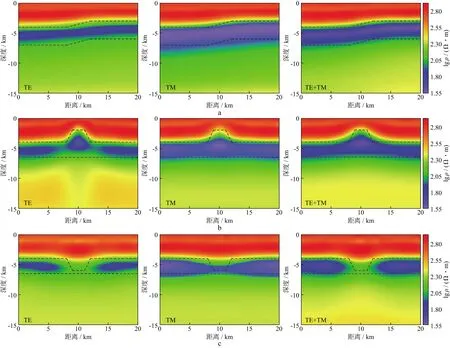
图4 隐伏构造模型不同极化模式的反演结果

3 应用实例

3.1 研究区概况

研究区为二连盆地苏尼特隆起东北部的朝克乌拉凹陷,该凹陷为北东向双断地堑型凹陷,南北以断层为界,呈NE45°方向展布,面积约3 800 km2。凹陷以低山丘陵地形为主,系典型的高原草场地貌,地势呈北高南低态势,海拔900～1 300 m,有一定的起伏,地表覆盖大面积火山岩,有少量小型湖泊分布。凹陷主要发育新近系、古近系、白垩系和侏罗系等4套地层,地层平均电阻率如表1所示。研究区目标储层为下白垩统巴彦花裙的赛汉塔拉组、腾格尔组以及阿尔善组地层,为一套低电阻率储层[21]。

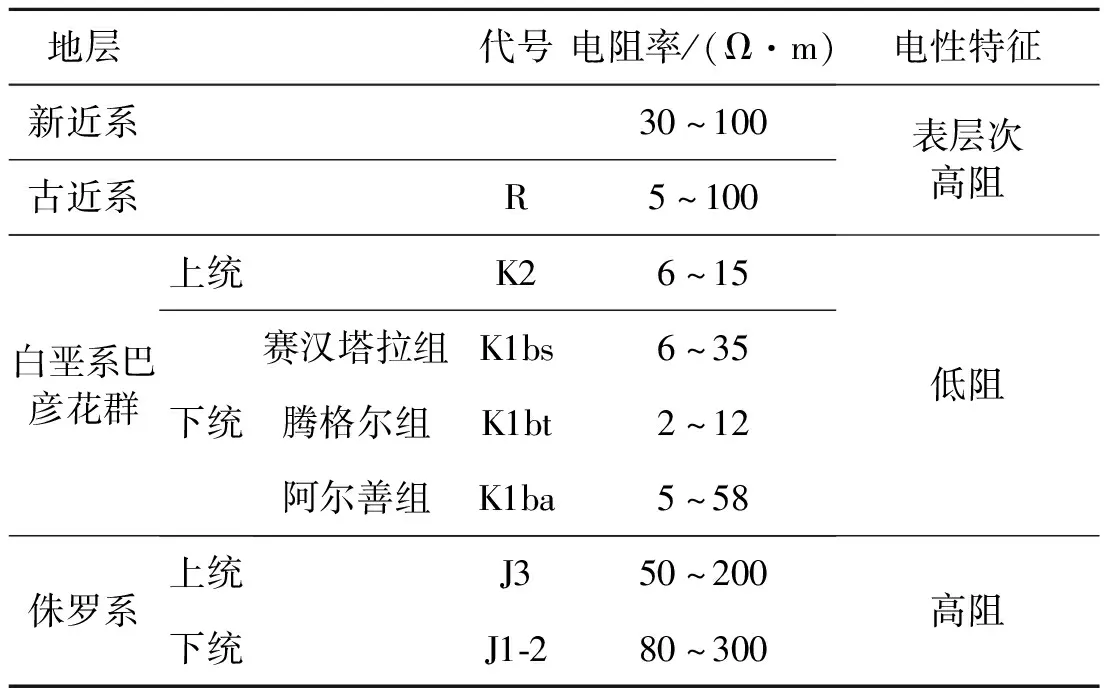
表1 朝克乌拉凹陷各地层电阻率资料

3.2 数据采集与处理

基于前期重、磁勘探结果,在朝克乌拉凹陷朝4次洼中部布设一条大地电磁测线,进行资料处理、反演与解释。该测线全长40 km,点距0.2 km,共201个测点。野外数据采集系统为V5-2000电法仪,采集方式为张量测量,每个测点采集5个电磁场分量,即Ex,Ey,Hx,Hy,Hz,下标x,y分别表示南北方向和东西方向。每站数据采集时间为24～30 h。

对采集的原始时间序列进行快速傅里叶变换处理,采用“Robust”估计计算得到功率谱数据,再经过一系列预处理,得到如图5所示的测点视电阻率和相位曲线。从图5可以看出,资料连续性较好,50 Hz工频干扰已被消除,实测资料品质有保障。

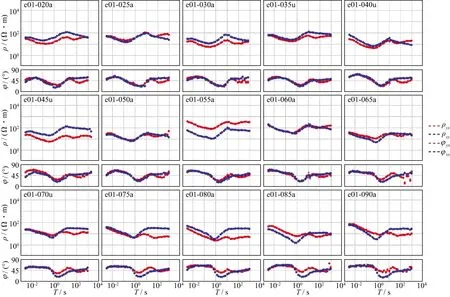
图5 部分测点实测大地电磁视电阻率和相位曲线

在进行大地电磁资料反演前,需要明确研究区构造的二维性及其电性主轴。我们采用Swift方法和共轭阻抗法,对实测资料进行维性分析,获得如图6所示的测线电性主轴统计测点分布云图[22]。图6中65号至220号测点,电性主轴总体明显确定,即在45°或-45°左右;而20号至64号测点,电性主轴不明显,在二维反演时需要认真编辑资料并注意TM、TE极化的选择。维性分析结果表明,测线处的地下电性结构具有较好的二维性,具备二维大地电磁反演条件。

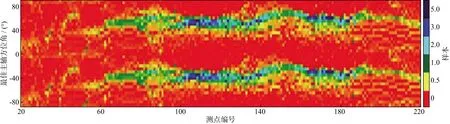
图6 大地电磁实测数据电性主轴统计测点分布云

3.3 反演与分析

应用大地电磁二维非线性共轭梯度反演算法,分别采用TE、TM、TE+TM极化模式数据,对该实测资料进行反演。基于凹陷各地层平均电阻率(表1)设置反演初始模型为:ρ1=100 Ω·m,h1=0.1 km;ρ2=20 Ω·m,h2=2 km;ρ3=300 Ω·m,h3=∞,经过30次迭代反演,不同极化模式耗时均为12 h左右,最终拟合误差为5.78%,5.16%,5.26%,获得的反演电阻率剖面如图7所示。

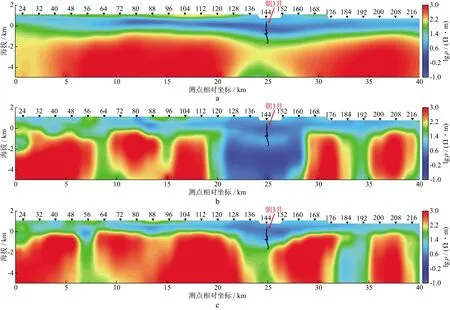
图7 朝克乌拉凹陷实测大地电磁二维反演的电阻率剖面

野外实测数据测线过朝3井旁,其中144号测点与朝3井邻近,对比朝3井电测井数据与144号测点不同极化模型反演电阻率数据(图8)发现,TE+TM极化模式的反演电阻率曲线与测井电阻率资料一致性最高,说明基于该极化模式的非线性共轭梯度反演方法用于凹陷类盆地实际大地电磁资料处理时,具有较好的应用效果。

对TE+TM极化模式的反演电阻率剖面进行地质解释,结果如图9所示。反演电阻率剖面由浅至深依次表现为次高阻—低阻(含极低阻层)—高阻的电性变化特征。受地表新近系火成岩影响,表层电阻率较高,一般高于50 Ω·m,火成岩主要分布于20号至128号测点,厚度为100～200 m,最大厚度在88号测点。地表200 m以下至海拔-2 000 m之间存在一套不等厚度白垩系低电阻率地层,该地层电阻率范围为4～50 Ω·m,最大厚度约3 500 m。该地层以40号测点、56号测点、88号测点及144号测点为中心,发育4个低阻洼陷区。依据朝3井电阻率分层数据(图8),以144号测点为中心的洼陷发育了腾格尔组2段、腾格尔组1段、阿尔善组4段及阿尔善组3段等地层,沉积构造整体表现为左陡右缓的“箕状断陷”结构,具有北断南超的结构特征,预测该洼陷含油气潜力最佳。白垩系地层以下,发育了侏罗系和古生界两套高阻地层,电阻率一般在300 Ω·m以上。从反演电阻率剖面整体来看,地层存在多处抬升与断陷,其中32号测点、96号测点及192号测点下方存在断裂,56号测点与144号测点下方为断陷。

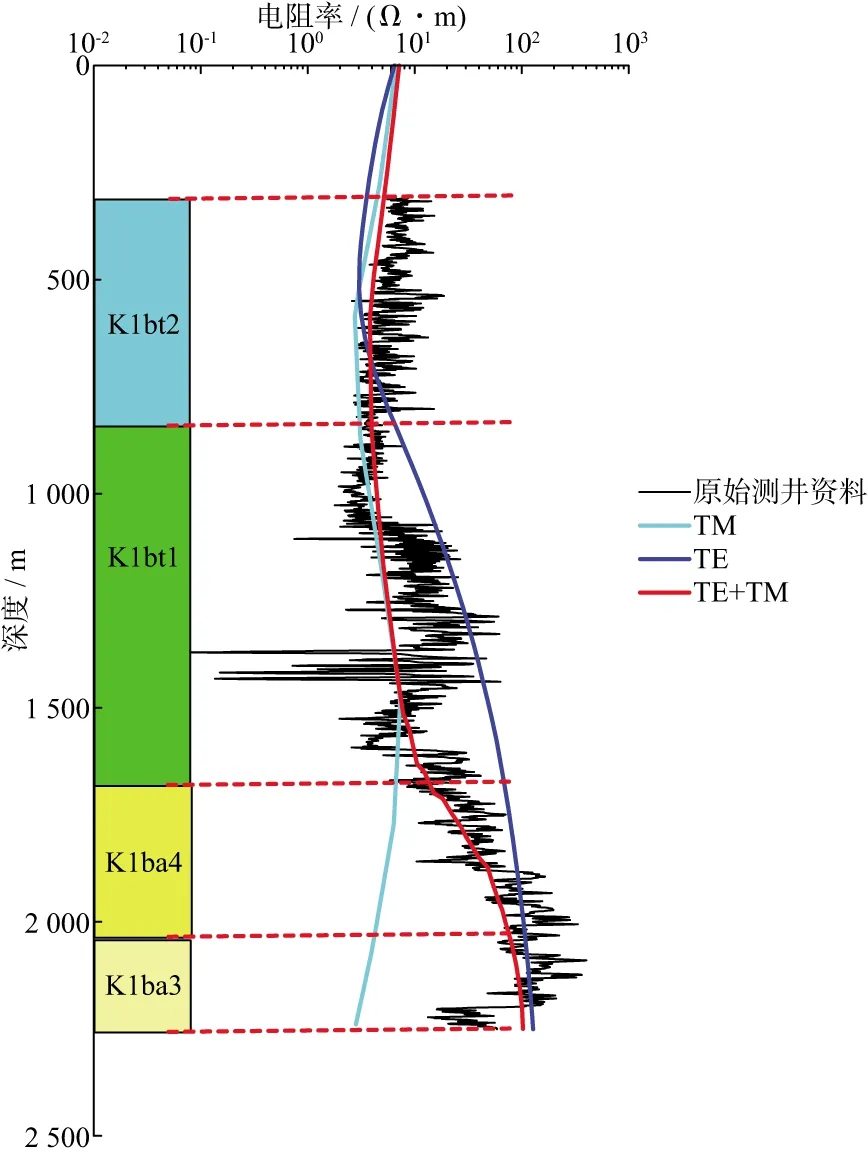
图8 朝3井电阻率曲线与144号测点反演电阻率曲线的对比

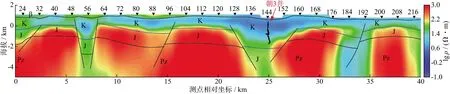
图9 朝克乌拉凹陷实测大地电磁二维反演电阻率剖面的地质解释结果

4 结论

本文开展了基于非线性共轭梯度法的不同极化模式大地电磁反演研究,通过正演模拟数据算法测试与实测资料反演,获得如下认识:

1)设置块体低阻模型和隐伏构造模型开展非线性共轭梯度反演算法测试,发现TE+TM极化模式反演电阻率剖面对异常体边界的刻画与反演精度优于TE、TM极化模式,且能够适用于地下复杂隐伏构造;

2)进行大地电磁实测资料反演前,需要进行数据维性分析,明确研究区构造维性及电性主轴方向,正确判别视电阻率与相位的TE、TM极化模式,并分别采用TE、TM、TE+TM的视电阻率和相位资料进行反演,通过与测井电阻率曲线对比,发现基于TE+TM极化模式的反演电阻率与测井资料吻合度最高;

3)采用非线性共轭梯度反演方法对朝克乌拉凹陷实测大地电磁资料进行处理,反演获得的电阻率剖面清晰地刻画了凹陷表层玄武岩分布、地层结构及基底构造形态,且与电阻率测井资料具有较好的一致性,表明该反演方法能够应用于凹陷类盆地的大地电磁资料处理解释,拓宽了电磁法在油气勘探领域的应用。