基于螺旋缠绕光纤的分布式声波传感三分量信号采集机理研究

曹丹平,律军军,孙上饶,马国旗,尹教建

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中国石油大学(华东)山东省深层油气重点实验室,山东青岛266580;3.哈利法大学文理学院,阿布扎比127788;4.中国石油大学(华东)理学院,山东青岛266580)

分布式光纤声波传感(DAS)技术是一种以光纤本身作为传感器,基于光的瑞利散射实现振动信号采集的新型光纤传感技术,具有成本低、测量精度高、不易受电磁干扰和安装简便等优点[1]。相比于常规单点式和准分布式传感器,DAS更适合用于长距离或时间及空间分辨率要求较高的应用场景,并在石油勘探、管道泄漏监测以及边防安全监测等方面被广泛应用。

近年来,研究人员致力于用DAS替代常规检波器进行微地震监测、浅地表地震勘探以及井中地震勘探等,并在基础理论、采集、处理和解释等领域取得了长足的进步[2-8]。但分布式声波传感的原理决定了DAS对光纤轴向应变敏感,而对径向应变不敏感,即直光纤DAS只能采集到沿光纤轴向方向的单分量振动信号[9-10]。随着地震勘探技术的进步,油气工业对三分量地震信号的采集需求越来越高,直光纤DAS只能采集单分量信号的特点,无法满足油气地球物理行业的地震资料采集需求。根据DAS光纤对轴向振动敏感的特点,如果将光纤的轴向方向分别调整到振动所在位置处的观测坐标系X,Y,Z3个正交方向,即可获得对应位置处的三分量振动信号,也就是光纤检波器的原理[11],但光纤检波器属于传统的单点探测,缺乏分布式传感技术能够开展连续采集的优势。受光纤检波器和分布式声传感技术的启发,在实际应用中,可以通过对光纤进行缠绕布置获得更加丰富的光纤轴向方向组合,即螺旋缠绕分布式光纤声波传感(HWC-DAS),从而在确保获得X,Y,Z3个方向振动信号的同时实现信息的连续采集。

HWC-DAS技术增强了DAS对不同方向分量振动信号的敏感性,可以采集到多分量振动信号,实现了对直光纤DAS技术的拓展,并推动了DAS技术在多分量地震勘探中的应用。在螺旋缠绕光纤多分量信号采集的基础理论研究方面,KUVSHINOV[12]对比了HWC-DAS中的光纤缠绕形状对DAS响应的影响,并分析了光纤与井壁在完全耦合或不耦合情况下体波、面波对DAS的角度敏感特征。NING等[13-14]先后提出利用沿单根和多根光纤测量的6个应变投影重建全应变张量的多分量DAS数据重构方法,讨论了不同标距长度对多分量应变信息恢复的影响,并通过数值模拟验证了该方法的有效性。INNANEN[15-16]在应变张量估计的背景下,提出一种沿任意弯曲的缠绕轴缠绕的螺旋光纤模型,并讨论了在多分量应变张量重建过程中标距长度和重建间隔对P波和S波信号重建的影响,该模型也被用于地震弹性波的正、反演[17-20]。WUESTEFELD等[21]在复杂速度模型中使用精确的射线追踪方法确定入射角,并进一步讨论了介质物性和DAS光缆包裹材料与最佳缠绕角之间的关系。

同时,在利用螺旋光纤开展多分量振动信号的采集与应用方面也得到了快速发展。KARRENBACH等[22]进行了井中三分量DAS数据的采集,并与常规三分量采集的数据进行了对比,表明了多分量DAS技术的应用潜力。HORNMAN等[23-24]利用螺旋缠绕光纤进行地震波数据采集,研究了HWC-DAS的角度敏感性,同时,对比了垂直分量检波器、HWC-DAS以及直光纤DAS采集的实际数据之间的差异,表明HWC-DAS对纵横波和面波均有较高的敏感性。在实际应用中,DAS采集的是应变数据,与常规动圈式或压电式检波器采集的数据既有联系也有差异,在地震资料处理过程中,为了实现同类型地震数据对比分析,可以将DAS采集到的应变信号或应变率信号转变为速度信号[7,19]或加速度信号。YURIKOV等[25]利用HWC-DAS对地震频带内的岩石物理属性进行测量,实验结果与传统仪器的测量结果吻合度较高,表明了DAS在岩石物理实验中的巨大潜力。陈亚峰等[26]采用螺旋缠绕光纤技术研究了热力管道泄漏监测系统,表明螺旋缠绕光纤技术有助于提高管线泄漏定位精度,具有良好的检测效果。

光纤的轴向敏感性导致光纤对不同类型的地震波具有不同的响应机理,从地震波的传播特征出发研究地震波入射角、速度特征和介质物性对光纤轴向应变的影响有助于更好地理解DAS在地震资料采集中的作用[12,27-29]。由于纵波和横波耦合在一起,在常规三维地震勘探中,采集到的是X,Y,Z3个相互正交的振动信号,需要通过对3个分量信号进行处理间接获得纵横波信息,因此,讨论螺旋光纤轴向应变与X,Y,Z三分量振动信号之间的关系有助于更好地与常规检波器采集到的资料进行对比。螺旋光纤采集到的振动信号相当于实际X,Y,Z3个方向的振动信号在光纤轴向方向上的投影,厘清光纤采集信号与实际三分量振动信号之间的理论关系对分布式光纤三分量地震信号采集具有重要的理论意义和指导作用。

本文聚焦光纤缠绕方式与三分量振动信号之间的关系开展基础研究,在假设螺旋光纤与缠绕轴完全耦合的前提下,首先,推导了螺旋缠绕光纤轴向应变与三分量振动信号之间的映射关系。然后,分析了不同条件下三分量振动信号对光纤轴向应变的影响。最后,采用波动方程模拟的三分量数字信号对螺旋光纤轴向应变所接收到的等效信号进行验证,并进行敏感性分析。

1 螺旋缠绕光纤三分量信号采集理论模型

1.1 螺旋缠绕光纤轴向应变的影响因素

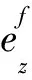
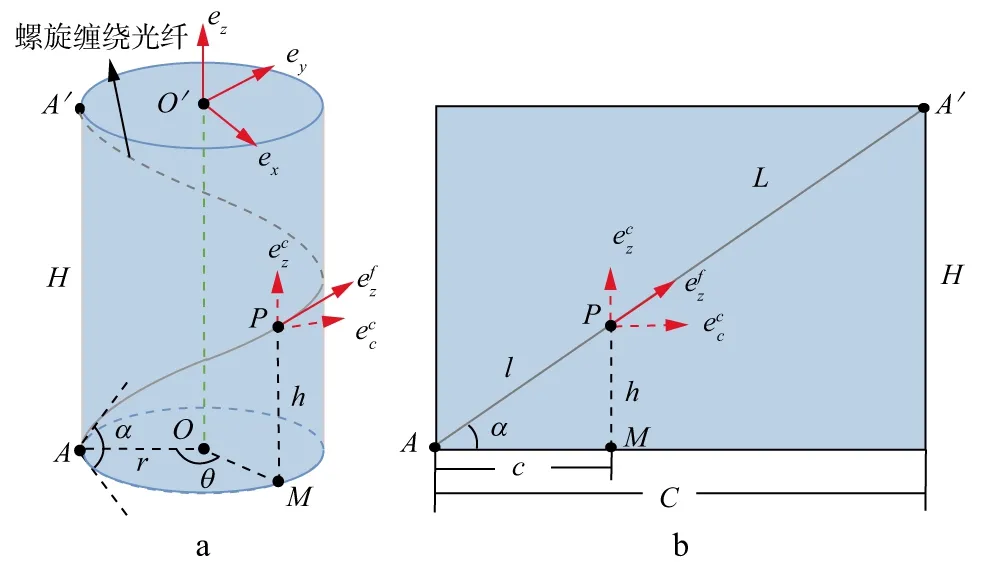
图1 DAS螺旋光纤缠绕几何模型

根据图1b所示几何关系,可以得到:

L2=C2+H2

(1)

对公式两边同时进行微分得到:

2L·dL=2C·dC+2H·dH

(2)

即

L·ΔL=C·ΔC+H·ΔH

(3)

等式两边同时除以L2,整理可得:

(4)

由于缠绕轴圆周周长C=2πr,ΔC/C=Δr/r,所以公式(4)可以表示为:

(5)

为了讨论方便,在完全各向同性介质中,可以采用从A点缠绕至A′点的整体应变来代表P点处的应变,即:

(6)

此时,螺旋光纤的轴向应变可表示为:

(7)

(8)

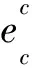
由公式(8)可定性地获得螺旋光纤轴向应变与真实地震波振动引起的实际三分量应变之间的关系,即当光纤缠绕角度α为固定值时,ezsin2α为定值,也就是说当DAS光纤以固定角度均匀绕轴缠绕时,螺旋光纤采集到的轴向应变中ez分量的绝对数值始终保持不变,而该分量在最终采集到的轴向应变总数值中所占比重则随着光纤缠绕角度的变化而变化;当光纤缠绕角度α增大时,cos2α的值逐渐减小,sin2α的值逐渐增大,螺旋缠绕光纤采集到的轴向应变信号中ez分量的占比增大,而ex和ey分量的占比则减小;即缠绕角越大,ez分量对螺旋缠绕光纤最终采集到的轴向应变信号影响越大,缠绕角越小时,则ex和ey分量对螺旋缠绕光纤最终采集到的轴向应变信号影响越大。

从图1中还可以看出,在一个缠绕周期内,光纤接收到的轴向应变还与光纤所在的空间位置有关。由于缠绕角α可以由h,l和c中的任意两个参数确定,也可以将螺旋缠绕光纤看作三维空间坐标系中由h,r和θ3个参数决定的螺旋曲线X(h,r,α),表示为:

X(h,r,α)=(h,rcosθ,rsinθ)

(9)

式中:θ为旋转角,该参数与h,r和α有关。

光纤在绕轴缠绕前行的过程中导致旋转角产生周期性的规律变化,为了探究θ与h,r和α之间的具体关系,由图1中一个缠绕周期内光纤上任意点P的位置可知:

(10)

(11)

由于图1b为图1a的平面展开,因此有:

(12)

根据图1b中几何关系有:

|AM|=|AP|cosα

|PM|=|AP|sinα

(13)

整理得:

rθ=l·cosα

h=l·sinα

(14)

公式(14)中的旋转角θ可以表示为:

(15)

将公式(15)带入公式(9),可以得到由h,r和α表示的螺旋缠绕光纤上任意点的三维空间位置关系公式:

(16)

式中:α∈(0,90°)。

由公式(16)可知,螺旋光纤缠绕后任意点P的位置可以由缠绕轴半径r、光纤缠绕角α和该点对应的缠绕轴高度h唯一确定,当然,缠绕轴高度h也可以用该点的光纤缠绕长度l代表,两个参数可以通过缠绕角直接转换,由于在每一个缠绕周期内缠绕角都是从0逐步增加到2π,因此后续的讨论将在一个周期范围内开展。

1.2 螺旋光纤轴向应变与三分量振动的映射关系

为了探究螺旋光纤轴向应变与三分量振动之间的映射关系,根据DAS螺旋缠绕光纤示意(图1),建立了如图2a所示的DAS螺旋光纤局部坐标系相对关系示意,图2b为光纤从A点缠绕到任意点P时所对应旋转角θ的示意。为了方便对比,在图中标注了A,A1,A2,A3,A′等5个特殊点,这5个点分别表示旋转角θ为0,π/2,π,3π/2和2π时所对应光纤上的点,通过这5个点有助于更加清晰地呈现光纤轴向应变在一个缠绕周期内的变化规律。首先定义地震波振动引起的实际三分量应变ex,ey,ez所在方向分别代表全局坐标系A-xyz中x轴、y轴和z轴的坐标方向。考虑到光纤对轴向应变敏感,为了便于讨论,沿光纤的轴向方向来定义局部坐标系,A-lAmAnA表示螺旋光纤上A点的局部坐标系,P-lmn表示螺旋光纤上P点的局部坐标系。其中,nA和n方向始终沿着光纤的轴向方向。

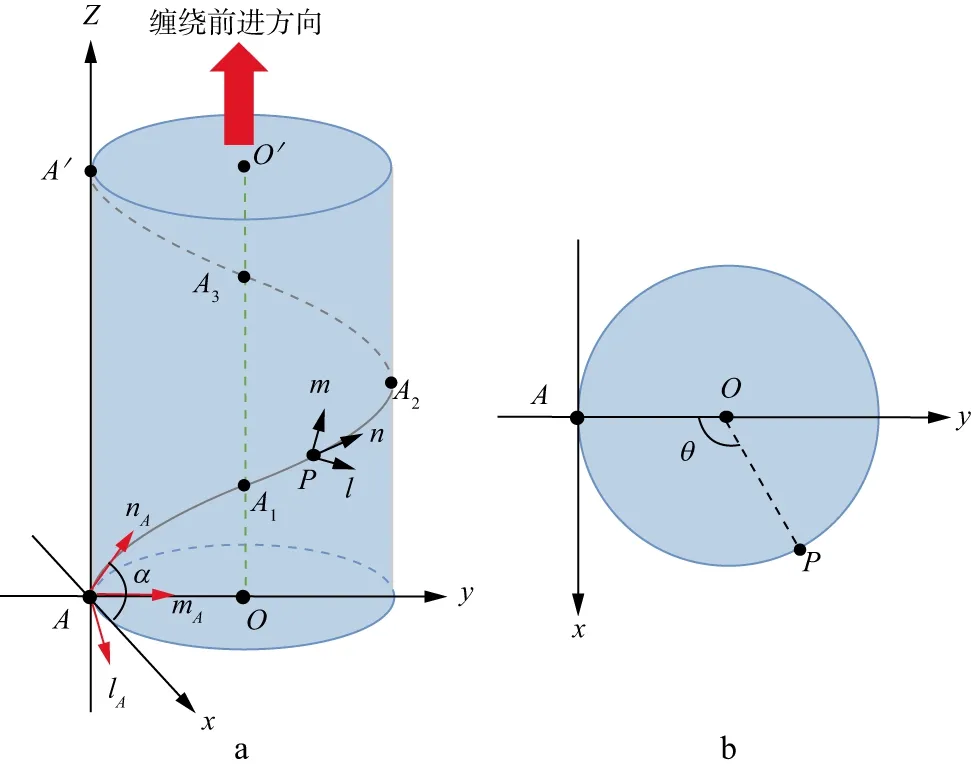
图2 DAS螺旋光纤坐标系相对关系示意(a)和P点所对应的缠绕角θ示意(b)

光纤上P点处的局部坐标系P-lmn可以看作是全局坐标系A-xyz通过坐标系旋转得到的。整个坐标旋转的过程可以分解为两步:①先沿着y轴正方向,将全局坐标系A-xyz的A-xz平面绕y轴顺时针旋转π/2-α,获得缠绕光纤在A点处的局部坐标系A-lAmAnA;②再沿着z轴正方向,将坐标系A-lAmAnA绕z轴顺时针旋转θ,即可获得P点处的局部坐标系P-lmn。

由于光纤对轴向应变敏感,因此,螺旋光纤上任意点处所测得的轴向应变实际上是地震波振动引起的X,Y,Z三分量应变在螺旋光纤所在点的轴向方向上的投影。根据本文定义,由地震波振动引起的实际三分量应变的方向和光纤轴向应变的方向分别为全局坐标系中3个坐标轴的方向和局部坐标系中n轴的方向,因此,求解该投影关系的关键在于准确确定局部坐标系中的n轴与全局坐标系中x轴,y轴和z轴之间的位置关系(图3)。

图3a展示了图2a中光纤轨迹上任意点所处局部坐标系中n轴绕z轴旋转的轨迹,其中A,A1,A2和A3分别表示旋转角θ为0,π/2,π和3π/2时,n轴所处位置点,根据图3中标注的关系可知,AA2平行于x轴,A1A3平行于y轴,nA表示螺旋光纤缠绕起点A的轴向方向,n表示螺旋光纤上任意点P的轴向方向,红实线箭头表示局部坐标系中n轴绕z轴旋转的运动方向;图3b中θnx,θny和θnz分别表示局部坐标系中的n轴分别与全局坐标系中的x轴、y轴和z轴之间的夹角。

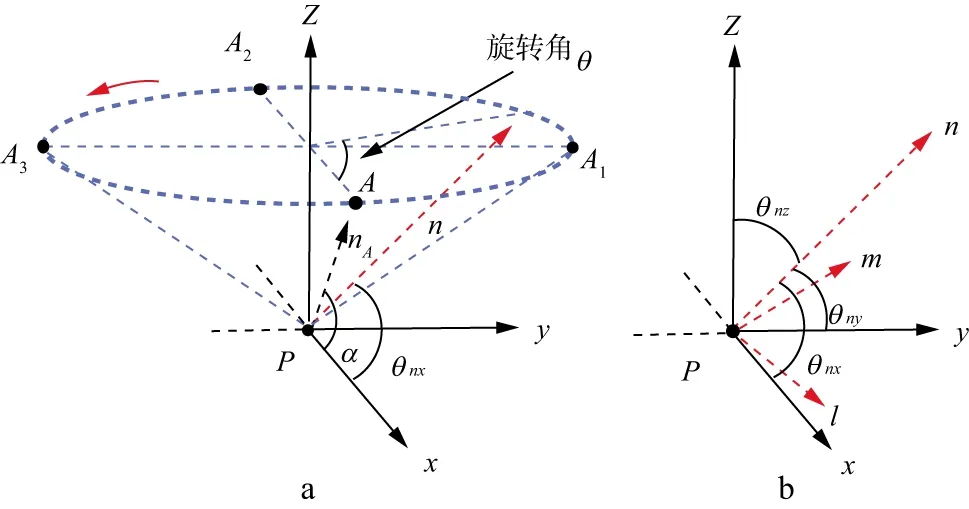
图3 局部坐标系中n轴绕z轴旋转轨迹示意(a)和n轴与全局坐标系坐标轴之间的夹角关系(b)

由图3a中局部坐标系中n轴绕z轴的旋转轨迹可知,局部坐标系中的n轴与全局坐标系z轴的夹角θnz不随旋转角θ的变化而变化,且仅与光纤的缠绕角有关,即

(17)

在局部坐标系n轴绕z轴旋转的同时,n轴分别与x轴和y轴的夹角θnx和θny随着旋转角θ以正弦(余弦)规律呈现出连续的均匀变化趋势,为了建立该变化规律,表1列出了光纤中任意点P缠绕至A,A1,A2,A3和A′点时,旋转角θ和夹角θnx之间的对应关系。

根据表1呈现出的规律性角度关系,可以采用三

表1 螺旋光纤旋转θ后旋转角与θnx之间的角度对应关系

角函数重建出如下的θnx随缠绕角α和旋转角θ之间的变化关系表达式:

(18)

同理可得:

(19)

将公式(15)带入公式(18)和公式(19)可得:

(20)

在获得局部坐标系n轴与全局坐标系坐标轴之间的夹角之后,可以构建全局坐标系A-xyz与局部坐标系P-lmn之间的旋转映射关系,采用上述所得的n轴与x轴,y轴和z轴之间的方位角关系,可以将坐标旋转矩阵表示为[30]:

(21)

式中:Rlx,Rly,Rlz,Rmx,Rmy,Rmz,Rnx,Rny和Rnz分别表示l轴,m轴,n轴与x轴,y轴和z轴之间的方向余弦。其中,影响光纤轴向应变的3个系数为:

Rnx=cosθnx

Rny=cosθny

Rnz=cosθnz

(22)

通过矩阵乘法,可以将全局坐标系A-xyz与局部坐标系P-lmn之间的映射关系表示为:

(23)

光纤上任意点的轴向应变与光纤所在位置处由地震波振动引起的实际三分量应变之间的关系可以表示为[30-31]:

e=Re0RT

(24)

式中:e表示局部坐标系中对应的应变张量;e0表示全局坐标系中对应的应变张量;R表示坐标旋转矩阵;RT表示坐标旋转矩阵R的转置。

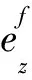
(25)

整理公式(25)可以得到螺旋光纤轴向应变与实际三分量应变之间的映射关系公式:

(26)

公式(26)也可以简写为:

m=Gm0

(27)

式中:m表示螺旋光纤轴向应变;G代表由旋转矩阵R得到的扩展矩阵;m0表示光纤所在位置处的实际三分量应变。

公式(27)代表了从实际三分量信号到螺旋光纤轴向应变之间的投影过程,反过来,在实际应用中就可以使用采集到的光纤轴向应变m重构光纤所在位置处的真实三分量应变m0,且理论上可以通过求取最小二乘解得到:

m0=(GTG)-1GTm

(28)

因此,在实际应用中,可以通过公式(28)来实现由螺旋光纤采集到的轴向应变重构出光纤所在位置处的实际地震波振动的三分量应变,此即利用螺旋缠绕光纤开展三分量信号恢复的理论依据。

2 螺旋缠绕光纤轴向应变对三分量应变的系数敏感性分析

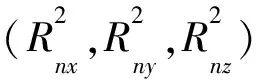
由图4可知,在缠绕角度α一定的条件下,螺旋光纤采集到的轴向应变中ez分量的值始终保持不变,ex和ey分量随着旋转角度的变化分别呈余弦和正弦的周期性变化,且无论在多大的缠绕角度下,两个分量随旋转角的正余弦的变化规律不会改变,但幅度会随着缠绕角度的增大而减小。随着缠绕角度α增大,螺旋光纤采集到的轴向应变中ez分量的值增大,但在一个旋转周期内的值均相同,而ex和ey分量的值逐渐减小,其值随旋转角的周期性变化规律保持不变。根据该变化规律可知,当缠绕角度较小时,光纤轴向应变中ez分量的影响较小,而ex和ey分量的影响较大,特别是当缠绕角度为0时,光纤轴向应变中采集到的ez分量为0,光纤轴向应变全部由ex和ey分量来确定,表明此时DAS光纤只能采集到径向应变信息;当缠绕角度较大时,光纤轴向应变中ez分量的影响增大,而ex和ey分量的影响减小,特别是当缠绕角度为90°时,此时螺旋缠绕光纤为直光纤,光纤轴向应变中只存在ez分量,无ex和ey分量。由此可见,随着缠绕角度α的增大,DAS螺旋光纤对地震波振动应变的ez分量敏感性逐渐增强,对ex和ey分量的敏感性逐渐减弱。

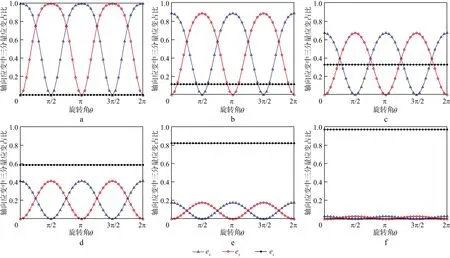
图4 缠绕角α分别为5°(a),20°(b),35°(c),50°(d),65°(e)和80°(f)时,螺旋光纤采集到的轴向应变中ex,ey和ez 3个分量的比重变化趋势

3 基于三分量振动信号的螺旋光纤轴向应变敏感性数值分析

为了进一步验证DAS螺旋光纤对地震波振动产生的三分量应变的敏感性变化规律,采用各向同性介质三维波动方程数值模拟得到的振动信号开展数值测试。为了便于对比和分析,选择了一个相位一致但振幅存在差异的三分量信号进行对比。其中,X,Y,Z3个分量的振动信号如图5a所示,3个分量所对应的振幅谱如图5b所示。

通过将X,Y,Z3个分量的振动信号投影到螺旋光纤的轴向应变方向上,即可获得螺旋光纤轴向方向上的应变特征,图6a对比了缠绕角度α分别为5°,35°和80°时螺旋光纤上采集到的轴向应变,图6b对比了3个不同缠绕角度下所采集到的信号振幅谱。

由图6a可知,当缠绕角度为5°时,螺旋缠绕光纤轴向应变振幅最大值明显低于ez分量应变的振幅最大值,但与ex和ey分量振幅最大值接近(类似图5a),且在图6b的振幅谱也具有相同的特点,即缠绕角较小时,螺旋缠绕光纤轴向方向上采集到的信号主要以X和Y分量成分为主,Z分量的影响较小。当缠绕角度增大到35°时,螺旋光纤轴向方向上获得的信号幅值和振幅谱特征开始逐渐接近ez分量的信号和振幅谱特征。而当缠绕角度增大到80°时,螺旋光纤轴向方向上获得的信号幅值十分接近ez分量的幅值,同时在振幅谱上也具有非常明显的接近趋势,即当缠绕角较大时,螺旋光纤轴向方向采集到的信号以Z分量信号为主。由此可见,随着缠绕角度α增大,螺旋光纤轴向方向采集到的信号中,Z分量的成分逐渐增多,而X和Y分量的成分逐渐减少。

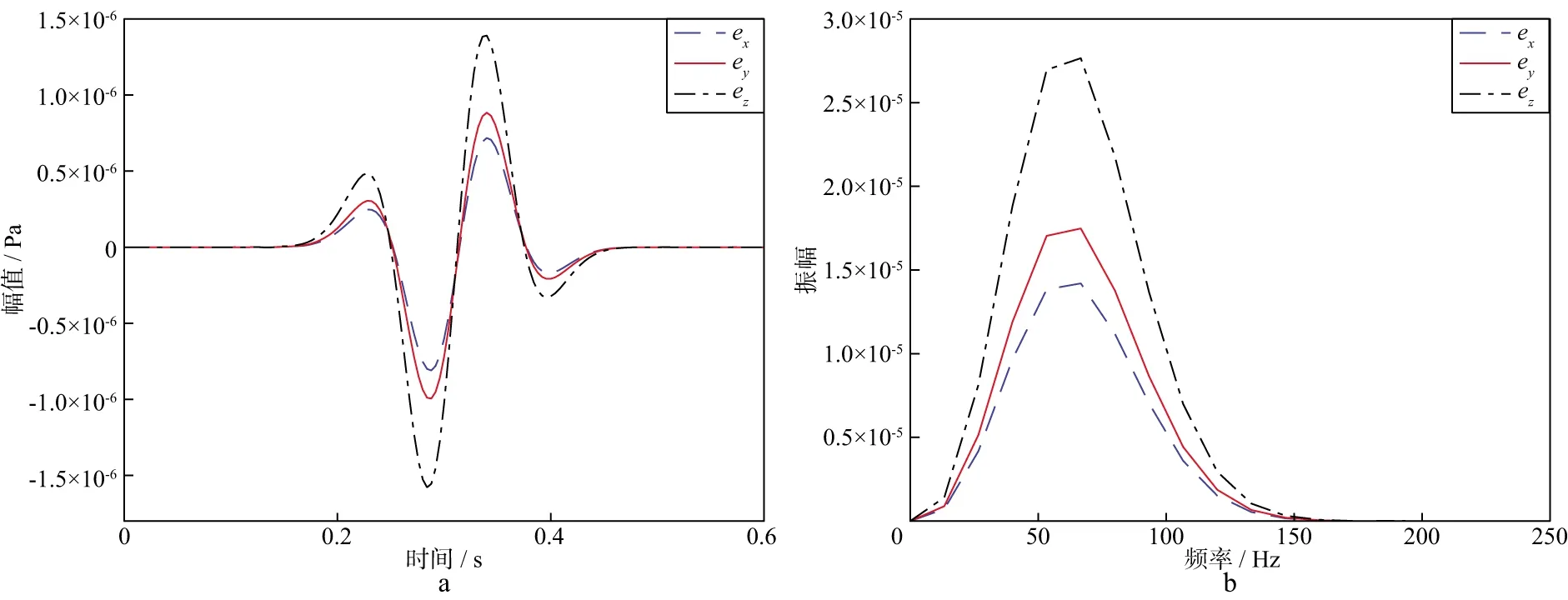
图5 DAS光纤所在位置处由地震波振动产生的三分量应变信号(a)及对应的振幅谱(b)

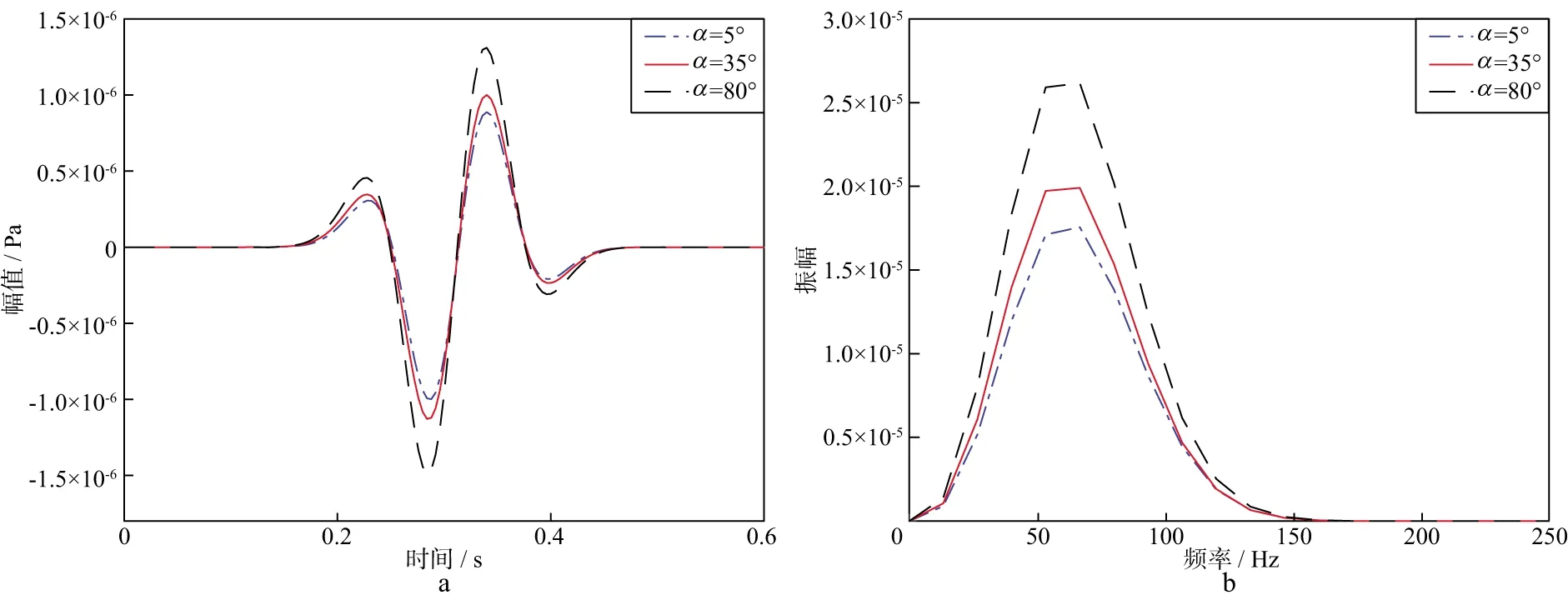
图6 不同缠绕角度时螺旋光纤轴向方向上采集到的信号(a)及对应振幅谱(b)

由此可见,X和Y分量在缠绕角较小的时候对螺旋光纤轴向方向的应变影响较大,由于X和Y两个分量随旋转角具有正余弦变化规律,为了进一步厘清X分量和Y分量对螺旋光纤轴向方向应变特征的影响,在小缠绕角条件下分别对两个特殊旋转角和π的位置开展数值测试。图7a展示了缠绕角度α为5°,旋转角度θ分别为π/2和π时螺旋光纤轴向应变上所采集到的应变,图7b展示了对应的振幅谱。

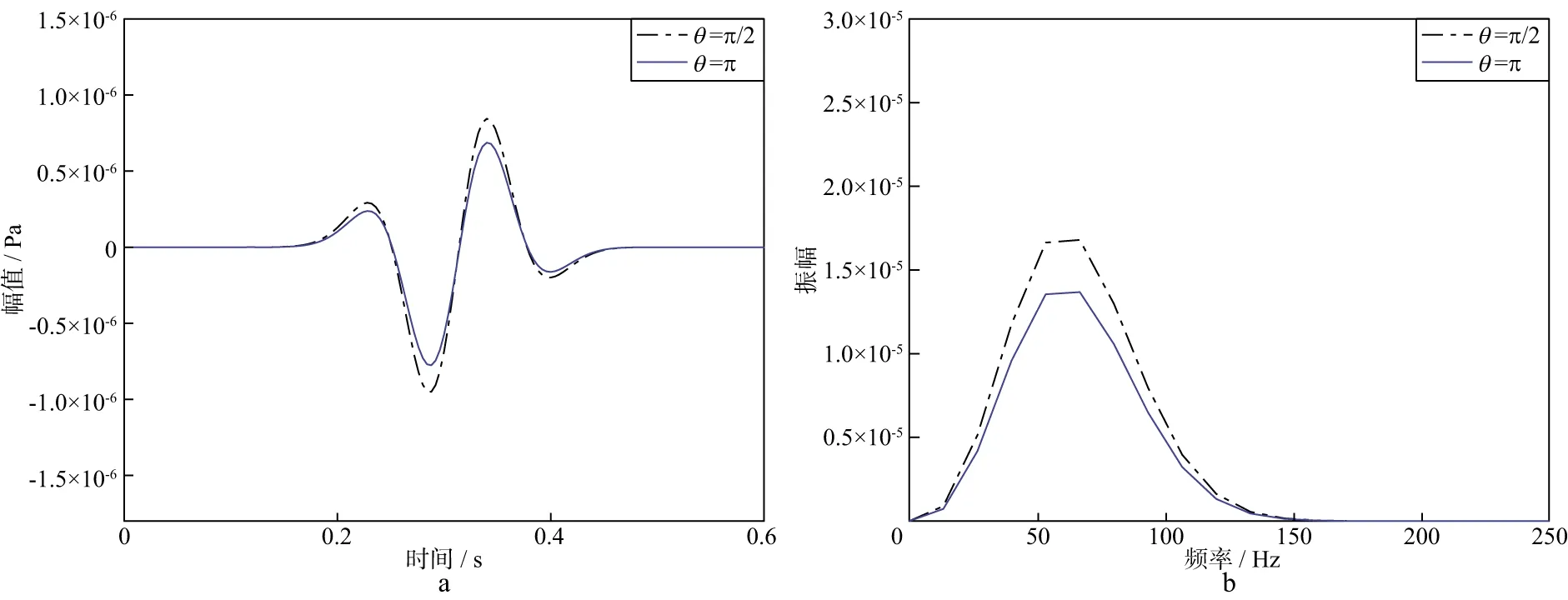
图7 相同缠绕角度不同旋转角条件下螺旋光纤轴向方向上采集到的信号(a)及对应的振幅谱(b)

由图7a可知,当旋转角度θ从π/2变化到π时,螺旋光纤轴向方向上采集到的应变幅值减小,同时振幅谱幅值也相应减小。依据图5可知,本例中由地震波振动产生的Y分量信号的幅值和振幅谱幅值均大于X分量信号,表明当旋转角度θ从π/2变化到π时,螺旋光纤轴向方向上获得的信号中X分量信号的影响增大,而Y分量信号的影响减小。同理当旋转角度θ从π增大到3π/2时,螺旋光纤轴向方向上获得的信号中X分量信号的影响减小,而Y分量信号的影响增大。由此可见,当缠绕角固定时,在一个缠绕周期内螺旋光纤轴向方向上采集的信号中的X分量信号的影响增大时,Y分量信号的影响将减小;而X分量信号的影响减小时,Y分量信号的影响将增大,两个分量信号对螺旋光纤轴向方向上采集到的信号特征具有一定的周期性和互补性。

4 结论

本文通过建立单根光纤螺旋缠绕的数学模型,推导了螺旋光纤轴向应变的表达式和螺旋光纤上任意点的三维空间位置关系式,明确了螺旋光纤轴向应变与光纤所在位置处3个方向真实应变之间的数学映射关系,并在螺旋光纤的一个缠绕周期内,定量分析了不同缠绕角度、不同旋转角度条件下三分量振动信号对光纤轴向应变的影响,并通过模拟的三分量数字信号对螺旋光纤轴向方向所接收到的有效信号进行了验证,得出如下结论:

1)螺旋缠绕光纤通过轴向方向的改变能够采集到光纤所在位置处的三分量振动特征,在光纤轴向方向上采集到的信号强度与实际三分量信号强度、光纤缠绕角度和光纤缠绕过程中各点所在的相对空间位置有关。

2)当光纤缠绕轴方向与Z分量信号方向一致时,随着光纤缠绕角度α增大,DAS螺旋光纤对沿缠绕轴方向的地震波振动(即Z分量)信号的敏感性增强,而对垂直于缠绕轴方向的(即X和Y分量)信号的敏感性减弱。当螺旋光纤的缠绕角度固定不变时,螺旋光纤获得的信号中Z分量信号不受旋转角度θ的影响,而X和Y分量信号则分别以余弦和正弦关系随旋转角度θ呈现出周期性的变化规律,两个分量在数值上具有互补性。

3)螺旋光纤采集到的信号取决于光纤上任意点的轴向方向与X,Y,Z3个分量之间的投影关系,上述结论在讨论时假设光纤缠绕轴方向与Z方向一致,可以直接适用于在直井中开展井中地震观测时的情况,而在地面地震勘探时通常可以将光纤缠绕轴方向调整至与地面平行的方向进行观测。在实际资料观测时,光纤缠绕轴方向与X,Y,Z3个分量可能均存在一定的夹角,但上述结论依然成立,不过规律性变化特征会减弱。

本文重点在均匀介质假设条件下讨论了X,Y,Z3个正交分量振动信号对螺旋缠绕光纤轴向应变的影响,对不同类型地震波在三维空间3个方向的振动信号具有普适性。实际地震勘探中广泛发育纵波、横波和面波等多种类型的波,不同类型的波在不同的传播方向上的振动分量差异较大甚至相位相反,容易导致螺旋光纤轴向应变上接收到的信号发生更加剧烈的变化,今后需要有针对性的单独讨论不同介质条件下不同类型地震波的传播特征和入射角等差异对光纤应变特征的影响,还应该充分考虑螺旋缠绕光纤的物性、标距长度以及光纤与缠绕轴之间的耦合程度等因素对螺旋光纤轴向应变响应的影响,从而有效提高螺旋缠绕光纤对不同类型地震波振动信号的采集能力,为真实三分量振动信号的有效恢复提供更加合理的依据。