连续能量核数据敏感性分析及其在AP1000中的应用

黄金龙，曹良志,*，贺清明，李 捷，沈 炜,2

(1.西安交通大学 核科学与技术学院，陕西 西安 710049；2.加拿大CANDU Owners Group)

核数据的敏感性分析是核数据不确定度量化的基础。相比于基于确定论程序的多群核数据敏感性分析[1]，基于蒙特卡罗程序的连续能量核数据敏感性分析具有几何适应性强、计算精度高等优势。近10年中，连续能量核数据敏感性分析在国际上取得了巨大进展。国际主流的蒙特卡罗程序，如MCNP[2]、Serpent[3]、SCALE[4]、McCARD[5]、OpenMC[6]等已具备连续能量核数据敏感性分析的功能，国内的蒙特卡罗程序RMC[7]也已具备此功能。从方法上看，MCNP首先采用反复裂变几率(IFP)方法进行连续能量核数据敏感性分析，此方法的优点是计算精度高，缺点是占用内存大、统计涨落较大。SCALE在此基础上提出了CLUTCH方法，有效降低了存储内存，但计算过程需要划分网格，计算存在近似。RMC提出了超历史法[8]以及基于裂变的CLUTCH等方法[9]提高计数效率。Serpent提出了碰撞历史法[3]，此方法是一种极具创新性的方法，可用于求解特征值灵敏度系数、广义灵敏度系数、共振参数的灵敏度系数和中子代时间的灵敏度系数等，同时Serpent还采用了扩展广义微扰理论[10]进行灵敏度系数的计算，该方法基于基函数展开，得到连续的函数形式的灵敏度系数公式，并基于连续形式的协方差信息，得到连续形式的响应参数的不确定度，使得灵敏度系数和不确定度结果实现“连续”。

本文在西安交通大学核工程计算物理实验室自主开发的蒙特卡罗程序NECP-MCX[11]中开发连续能量核数据敏感性分析的功能模块。采用反复裂变几率方法求解灵敏度系数，并使用稀疏矩阵的存储方式以及重叠块法分别降低存储内存和提高计数效率，最后开展AP1000堆芯keff对连续能量核数据的敏感性分析研究。

1 理论方法

本文从中子输运方程出发，推导keff对连续能量核数据的灵敏度系数计算公式，并结合蒙特卡罗程序模拟的特点，利用反复裂变几率方法得到共轭通量，从而在前向蒙特卡罗模拟中得到keff对连续能量核数据的灵敏度系数。

1.1 一阶微扰理论

稳态中子输运方程可表示为：

(1)

其中：B为输运-碰撞项算子；ψ为中子通量密度；k为有效增殖因子；F为产生项算子。

输运-碰撞项算子B表示为：

Ω′→Ω)ψ(r,Ω′,E′)dE′dΩ′

(2)

产生项算子F表示为：

ψ(r,Ω′,E′)dE′dΩ′

(3)

同样，稳态共轭中子输运方程可表示为：

(4)

共轭输运-碰撞项算子B*表示为：

Ω→Ω′)ψ*(r,Ω′,E′)dE′dΩ′

(5)

共轭产生项算子F*表示为：

ψ*(r,Ω′,E′)dE′dΩ′

(6)

引入扰动：

F′=F+δF

B′=B+δB

k′=k+δk

ψ′=ψ+δψ

(7)

则扰动后的中子输运方程表示为：

(8)

将式(8)两边与ψ*在相空间中内积，得到：

〈ψ*,k′B′ψ′〉=〈ψ*,F′ψ′〉

(9)

将式(1)两边与ψ′在相空间中内积，得到：

〈ψ*,(kB-F)ψ′〉=〈ψ′,(kB*-F*)ψ*〉

(10)

根据式(9)、(10)以及共轭算子的性质，采用一阶近似可得到：

(11)

灵敏度系数的定义为：

(12)

将式(11)代入式(12)，可得到：

(13)

对式(13)分子中的3项以及分母分别展开，可得到裂变项：

(14)

散射项：

Ω′→Ω)ψ(r,Ω′,E′)dΩ′dΩdr

(15)

碰撞项：

Σx(r,E)ψ(r,Ω,E)dΩdr

(16)

分母表示为：

Σf(r,Ω′,E′)ψ(r,Ω′,E′)dE′dΩ′·

(17)

针对具体的核数据，根据式(14)～(17)的组合可得到keff对该核数据的灵敏度系数。

1.2 反复裂变几率

从式(14)～(17)可看出，求解连续能量核数据的灵敏度系数需得到共轭通量以及核反应率，统计核反应率在蒙特卡罗程序中易实现，因此求解灵敏度系数的关键在于求解共轭通量。

Hurwitz[12]首先解释了反复裂变几率的物理含义：在相空间(r，Ω，E)处引入1个中子，称为祖先中子，经过数代蒙特卡罗模拟后，由该祖先中子产生的后代中子数目会达到稳定，后代中子的数目即为(r，Ω，E)处的反复裂变几率，具体过程如图1所示。可证明，相空间中某点(r，Ω，E)的反复裂变几率正比于该点的共轭通量，由于式(13)中分子和分母同时包含共轭通量，因此可直接用反复裂变几率代替式(13)中的共轭通量。基于反复裂变几率方法可直接在前向蒙特卡罗模拟中得到共轭通量。蒙特卡罗模拟中使祖先中子产生的后代中子数达到平衡所需要的蒙特卡罗代数称为块，块的大小由问题决定，一般块的大小取5～20。在1个块中，将蒙特卡罗代分为初始代、过渡代和渐近代，在初始代中统计核反应率，并对祖先中子进行编号，过渡代中传递祖先中子的编号信息，渐近代统计后代中子的数目。因此，1个块由数个蒙特卡罗代组成，经过1个块的模拟，可得到1次灵敏度系数的计数。

图1 反复裂变几率原理示意图Fig.1 Schematic diagram of iterated fission probability

由于需要统计数代后的中子数目，需在数代之后才能得到共轭通量的计数，无法在蒙特卡罗模拟的当代得到共轭通量的计数，且核反应率与共轭通量的乘积与粒子相关，因此需存储与模拟粒子数相关的核反应率计数数组。当粒子数较大、计算的灵敏度系数较多时，内存占用非常大。对于VERA 1B算例，总代数为500代，其中非活跃代设置为200代。数值结果表明，当粒子数大于100时，核反应率数组非零值比例达到稳定，即不再变化，因此本测试粒子数取为100，在2群和44群能群划分下统计不同核素不同反应道的核反应率，其非零值比例列于表1。

表1 核反应率计数数组非零值比例Table 1 None-zero value rate in reaction rate array

从表1可看出，核反应率计数数组中非零值的比例与能群结构有关。在2群能群结构下，由于能群划分较粗，非零值比例较大，达到82%。而在44群能群结构下，核反应率计数数组中非零值的比例最大仅为15%，因此核反应率数组中存储的大部分数据是对结果没有明显意义的零值，可采用稀疏矩阵的方式存储核反应率计数数组，以达到降低内存的效果。

在反复裂变几率方法中，不同的块依次相连称为等待法，由于需用渐近代统计得到的共轭通量对初始代统计得到的核反应率进行加权，才能得到1次灵敏度系数的计数，因此等待法计数效率较低。而重叠块法[13]中块与块之间有重叠，第i代的中子，既处于第i块的初始代，也是第i-B+2块至第i-1块的过渡代(B表示块的大小，i>B)，同时也是第i-B+1块的渐近代，块的数量明显增多，因此能提高计数效率。等待法和重叠块法示意图如图2所示。如果将蒙特卡罗模拟的条件设置为300代活跃代、块的大小取10，采用等待法进行计算，灵敏度系数计数次数为30，而采用重叠块法进行计算，灵敏度系数的计数次数为291。

图2 等待法和重叠块法区别Fig.2 Difference of waiting method and overlapping block method

由于蒙特卡罗模拟中随机变量的统计标准差σ满足：

(18)

其中，N为试验次数。因此，采用重叠块法计数的试验次数N大于等待法，重叠块法计数的统计涨落小于等待法。

2 程序验证

根据前文介绍的基于重叠块法的反复裂变几率方法、稀疏矩阵存储方式，在蒙特卡罗程序NECP-MCX上完成keff对连续能量核数据敏感性分析功能模块的开发，对VERA 2B算例进行验证，并将NECP-MCX的灵敏度系数计算结果与MCNP6进行对比。

2.1 算例设置

本文选取的验证算例取自VERA系列基准题，VERA 2B算例布置如图3所示。具体几何以及材料信息参见基准题手册[14]。

图3 VERA 2B俯视图Fig.3 Top view of VERA 2B

将蒙特卡罗模拟的计算条件设置如下：总代数为500代，其中非活跃代设置为200代，活跃代设置为300代，采用ENDF-B/Ⅶ连续能量点截面数据库，块的大小取5，每代模拟的粒子数为1×105。

2.2 计算结果

根据上述算例设置，利用NECP-MCX计算得到VERA 2B算例中keff对核数据的积分灵敏度系数及69群勒平均灵敏度系数，并将计算结果与MCNP6进行对比。所得keff对核数据的积分灵敏度系数列于表2。

表2 VERA 2B算例中keff对核数据的积分灵敏度系数Table 2 Integrated sensitivity coefficients of keff to nuclear data in VERA 2B problem

由表2可发现，除1H-σelas和1H-σt外，对于其他核数据的灵敏度系数，NECP-MCX和MCNP6的计算结果相对偏差均小于1%，而1H-σelas和1H-σt的灵敏度系数计算结果相对偏差分别为-2.99%和-4.12%。这是由于弹性截面的灵敏度系数计算涉及到式(13)分子中的第2项和第3项，当两项的量级相当时，两项相减会导致统计涨落(相对标准差)较大[15]。MCNP6计算得到的1H-σelas和1H-σt的灵敏度系数的相对标准差也较大，分别为2.90%和4.04%，而NECP-MCX和MCNP6对这两个核素的灵敏度系数计算结果相对偏差小于MCNP6计算结果的3σ，因此可认为两者积分灵敏度系数计算结果符合得较好。

由表2还可发现，MCNP6计数的相对标准差是NECP-MCX的2.18～2.63倍。这是由于MCNP6使用的是等待法，在当前计算条件设置下，灵敏度系数的计数次数为60，而NECP-MCX使用的是重叠块法，在相同计算条件设置下，灵敏度系数的计数次数为296。根据式(18)可得到，理论上对于同一灵敏度系数的计算，MCNP6的统计涨落是NECP-MCX的(296/60)1/2=2.22倍，这一结果与实际统计结果相符。采用重叠块法，统计涨落降低，相应的计算时间增加，本文未统计计算时间，但根据文献[13]结果，重叠块法的品质因子(FOM)大于等待法。

对灵敏度系数分69群统计，可得到69群勒平均灵敏度系数，如图4所示。

对比图4中69群勒平均灵敏度系数可发现，NECP-MCX的计算结果基本上都落在MCNP6计算结果的3σ内，证明NECP-MCX的灵敏度系数计算结果与MCNP6的吻合较好。同时可发现，对于1H-σelas的勒平均灵敏度系数结果，存在较大统计涨落，同样是由于在计算灵敏度系数时两项相减所致，且在能群划分更细时，每个能群内的计数更少，灵敏度系数结果更难收敛。

图4 VERA 2B算例中keff对不同核数据的69群勒平均灵敏度系数Fig.4 69g sensitivity coefficients per unit lethargy of keff to nuclear data in VERA 2B problem

通过上述对VERA 2B算例积分灵敏度系数和69群勒平均灵敏度系数的计算结果对比，可证明，NECP-MCX计算得到的keff对核数据的灵敏度系数结果与MCNP6吻合较好。

3 AP1000计算结果

本文用NECP-MCX对AP1000反应堆首循环进行建模计算，反应堆处于控制棒全提状态，利用NECP-MCX的画图功能得到AP1000的堆芯布置图，如图5所示。

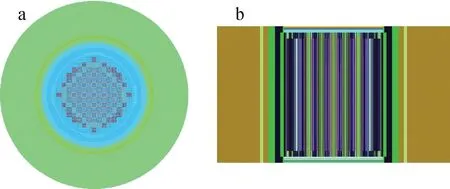
图5 AP1000堆芯俯视图(a)和左视图(b)Fig.5 Top view (a) and left view (b) of AP1000 core

蒙特卡罗模拟的计算条件如下：每代粒子数设置为2×106，共1 000代，其中前500代为非活跃代，采用ENDF-B/Ⅶ连续能量点截面数据库，块的大小取5。所得AP1000堆芯keff对连续能量核数据的积分灵敏度系数列于表3。

由表3可发现，对AP1000堆芯keff最敏感的核数据分别是235U-ν、235U-σf、235U-σt、238U-σγ、1H-σelas和10B-σt。这是由于235U和238U是首循环燃料中的主要组成核素，其平均裂变中子数和裂变截面直接影响中子的产生，对keff产生直接的影响，同时AP1000燃料富集度为3%～5%，燃料中238U的比例高达95%，其俘获截面较大，会吸收较多的中子，从而影响keff，且keff的灵敏度系数为负。1H是慢化剂H2O中的核素，通过弹性散射达到慢化的效果，1H的弹性散射截面越大，其慢化中子的能力越强，反应堆中的慢中子越多，发生裂变反应的中子越多，使得keff越大。10B作为硼酸中的主要核素，在反应堆中用于控制反应性，具有较大的中子吸收截面，因此其总截面灵敏度系数为负。

选取表3中积分灵敏度系数绝对值较大的6个反应道，得到其69群勒平均灵敏度系数，如图6所示。

表3 AP1000算例中keff对核数据的积分灵敏度系数Table 3 Integrated sensitivity coefficients of keff to nuclear data in AP1000 problem

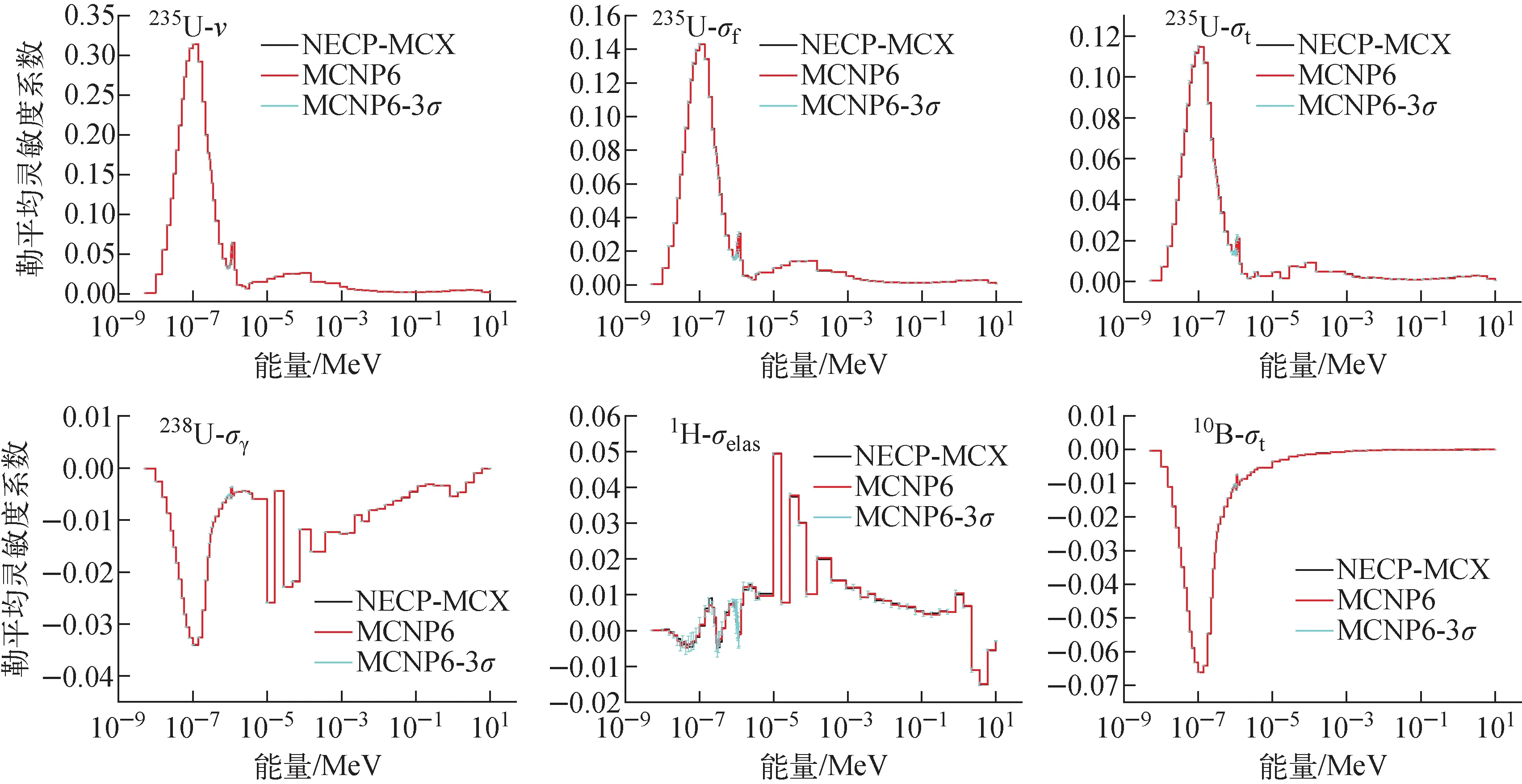
图6 AP1000算例中keff对不同核数据的69群勒平均灵敏度系数Fig.6 69 groups sensitivity coefficients per unit lethargy of keff to nuclear data in AP1000 problem

从图6可看出，NECP-MCX的计算结果与MCNP6符合得较好。灵敏度系数的形状与VERA 2B 算例中69群勒平均灵敏度系数的较近。根据得到的69群灵敏度系数以及数据库中的协方差矩阵信息，基于“三明治”法则，便可计算得到核数据的不确定度对AP1000堆芯keff计算带来的不确定度大小，用于后续的安全分析。

4 总结

本文基于一阶微扰理论推导了keff对核数据的灵敏度系数公式，采用反复裂变几率方法在蒙特卡罗的前向模拟中求解共轭通量，无需执行共轭计算。采用稀疏矩阵的存储方式和重叠块法分别达到降低存储内存和降低统计涨落的效果。基于上述理论和方法，在NECP-MCX上完成了连续能量核数据敏感性分析功能模块的开发，并对VERA 2B算例进行了验证。结果表明，NECP-MCX的灵敏度系数计算结果与MCNP6的吻合较好。最后基于AP1000堆芯进行了keff对核数据的敏感性分析计算，得到了对keff最敏感的核数据，分别是235U-ν、235U-σf、235U-σt、238U-σγ、1H-σelas和10B-σt。根据得到的灵敏度系数和数据库中已有的协方差矩阵信息，基于“三明治”法则，便可得到核数据的不确定度对AP1000堆芯keff计算导致的不确定度，用于后续的安全分析。