滚塑工艺在加热阶段的两种传热模型的比较研究

叶冬蕾，刘学军，王 晓

（北京工商大学人工智能学院，北京 100048）

0 前言

本文研究的加热阶段是指从滚塑模具在烘箱内开始受热到其内部粉料开始熔融之间的这一段过程，并将该过程所花费的时间简称为加热时间。在加热阶段，粉料颗粒与内部空气一边运动，一边混合。模具内壁面、粉料颗粒、内部空气三者彼此之间都有对流换热或导热。在加热过程，滚塑模具表面和模具内部的温度不仅与模具的几何形状和尺寸大小、模具材料与粉料的物性参数、粉料的质量有关，应该还与模具转动的方式与转速有关。这是因为后者直接影响了粉料和空气在模具内部的混合程度与运动状态。Olinek等[1]通过实验研究了单轴转动的圆筒形模具内部粉料的运动情况，根据模具转速由低到高依次将粉料的运动状态分为5种情况，分别是滑动状态、雪崩状态、翻滚状态、瀑布状态、离心状态。Nguyen等[2]应用光滑粒子流体动力学方法（SPH）模拟了粉料在圆筒形滚塑模具内部的流动状态，其计算结果与实验结果吻合较好。但在他们的计算中也没有考虑任何传热的因素。

由于在加热阶段，滚塑模具内部的粉料与空气的混合过程是运动和传热机理都非常复杂的气固两相流，因此通过建立传热理论模型来研究粉料的运动状态对滚塑加热过程的影响是比较困难的。目前已有的滚塑传热模型都不考虑模具内部粉料的运动状态。根据这些模型对粉料运动的处理方式，可以大致上将其分为两类——tumbling模型和static bed模型。tum⁃bling模型[3⁃5]假设粉料与空气混合非常均匀，整个混合物与模具内壁面发生对流换热。static bed模型[6⁃8]假设加热过程刚一开始，粉料就均匀紧密地黏附在模具内壁面上，即认为粉料在模具内部是离心运动状态。而在这一粉料层内部包裹的是内部空气。该模型的传热机理是模具内壁面与粉料层进行导热，而粉料层同时与内部空气进行对流换热。由于滚塑模具的转速比较慢，一般情况下粉料的运动状态不会出现离心模式。因此在粉料开始熔融前的加热阶段，static bed模型与实际情况相差较大，故不在本文的研究范围内。

本文将采用两种传热模型来分别仿真计算圆筒形模具表面及其内部的温度，即所谓的模具温度和模内温度。并将计算结果与实验结果相比较，以分析每种传热模型计算误差产生的原因。第一种传热模型是在传统tumbling模型的基础上改进所得。在第一种模型中不是简单地将粉料和内部空气的混合物当成是同一种的单相流体，而是把这两者的运动当成是由两种不同流体组成的两相流流动。显然该模型比传统的tum⁃bling模型更符合实际，同时又避免了追究粉料颗粒运动细节所带来的计算复杂性。第二种传热模型是在传统tumbling模型的基础上做了两点简化。一是忽略了模具的温度梯度，二是忽略了模具外形的影响。这样就可以对模具及其内部混合物列出常微分形式的能量守恒方程，数学求解变得非常容易。由于模具的厚度远远小于其平均半径，另外模具的热导率也远远大于内部空气和粉料的热导率，因此上述两点简化是合理的。本文对这两种传热模型的比较研究可以为滚塑工艺加热阶段的理论分析和仿真计算提供理论依据。

1 计算参数及实验结果

如图1所示，圆筒形钢制模具在电机带动下绕轴线O做单轴旋转，其内部装有质量为0.21 kg的聚乙烯粉料。模具的外表面被通电的加热带均匀加热，其热流密度为6.9 kW/m2。钢制模具的内径为92 mm，壁厚为2 mm，其内部空间的轴向长度为146 mm。粉料的表观密度为317 kg/m3，热导率为0.1 W/（m•K），环境温度下的比热容为660 J/（kg•K）。模具和粉料的初始温度均为10℃。采用圆柱坐标系研究该流动与传热问题。如图1所示，r为径向坐标，θ为周向坐标，轴向坐标z过轴心O并与纸面垂直。

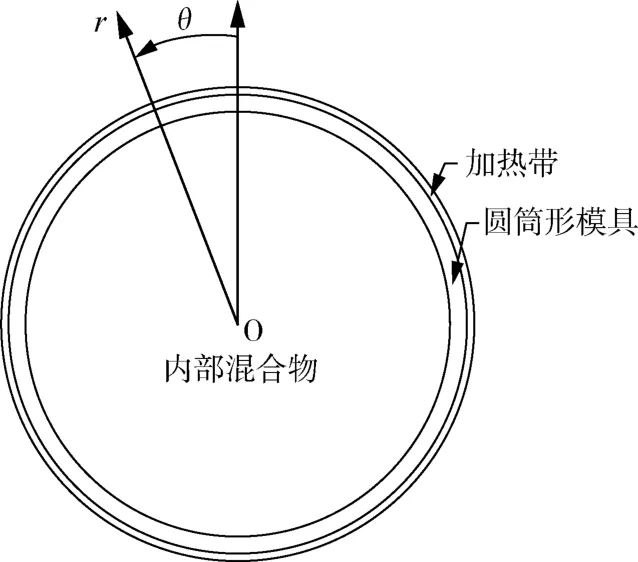
图1 圆筒形滚塑模具的横截面示意图Fig.1 Schematic of cross⁃section of cylindrical rotational mold

图2给出了模具外表面及其内部的实测温度随加热时间的变化规律。上述两种传热模型的仿真结果将与图2所示的实验结果进行比较。

图2 滚塑模具外表面及其内部的实测温度Fig.2 Tested temperatures of outside surface and internal space of rotational mold

2 传热模型

2.1 第一种传热模型

如果想要精确地研究粉料和内部空气的混合过程和运动状态，则需要跟踪粉料颗粒的运动轨迹，并考虑粉料颗粒与内部空气之间的各种相互作用力，那么就必须采用两相流的欧拉⁃拉格朗日法来进行仿真。虽然该种方法的计算精度高，但计算量和计算难度非常大。在本模型里，不是将粉料看成固体颗粒，而是看成另一种连续的流体介质。由于一般情况下滚塑粉料的颗粒很细小，在模具内部空间的分布范围较广，所占的体积百分比也超过10%，因此将粉料看成连续的流体跟实际情况的差异并不大。这样就可以采用两相流的欧拉⁃欧拉法来仿真粉料和空气在模具内的流动与传热。本文将采用FLUENT软件中多相流功能模块里的Mixture模型来进行上述的仿真计算，它是欧拉⁃欧拉法中最简单的一种计算模型。

如图1所示，第一种传热模型的计算区域包括模具本身和模具内部的由粉料和空气组成的混合物。将粉料看成连续的流体就需要给其赋予相应的物理性质参数。粉料流体的密度、热导率和比热容采用前述第1节中所给出的物性参数。但目前被看作流体的粉料的黏度系数没有任何实验数据可供查询，也无法由精确的计算公式得出，本文将采用式（1）[9]近似计算粉料流体的黏度系数。

式中μa——内部空气的动力黏度，Pa•s

μp——粉料流体的动力黏度，Pa•s

ρa——内部空气的密度，kg/m3

ρp——粉料的表观密度，kg/m3

2.2 第二种传热模型

在第二种传热模型里，假设粉料与内部空气充分混合，即在任意时刻内部混合物的温度与内部空气的温度和粉料的温度都相等。由于滚塑模具的壁厚很小，因此可以忽略模具壁的温度梯度。也就是说在本传热模型里，内部混合物和模具的温度都只随时间变化，而与空间位置坐标无关。根据能量守恒原理可知，电加热带传给模具的热量等于模具内能的增量与内部混合物内能的增量之和，同时模具与内部混合物的对流换热量等于内部混合物内能的增量。由此可以得到式（2）和式（3）。初始条件为t=0，Tm=Tap=T0。

式中Ai——模具内壁面的面积，m2

AO——模具外壁面的面积，m2

cap——内部混合物的定压比热容，根据内部空气和粉料的质量比按式（4）计算所得，J/（kg·K）

式中ca——内部空气的定压比热容，J/（kg·K）

cm——模具的定压比热容，J/（kg·K）

cp——粉料的定压比热容，J/（kg·K）

hi——模具内壁面与内部混合物间的平均表面传热系数，W/（m2·K）

Ma——内部空气的质量，kg

Mm——模具的质量，kg

Mp——内部粉料的质量，kg

q——模具外壁面的热流密度，W/m2

t——时间，s

T0——模具和内部混合物的初始温度，℃

Tm——模具的温度，℃

Tap——内部混合物的温度，℃

圆筒形模具内壁面上在加热阶段的平均传热系数hi可按式（5）计算。关于该公式的使用方法以及Nu数和Pr数的定义式详见文献[10]。

式（2）和式（3）是简单的线性常微分方程，计算量很小，可直接采用MATLAB软件求解。为减小仿真计算的难度，在应用上述这两种传热模型时，都先假设粉料具有常物性，即统一采用初始温度为10℃时的物性参数。后面还会在考虑粉料的物性参数随温度变化的情况下分别采用这两种传热模型再次进行仿真计算，并通过计算结果与实验结果的比较来分析粉料变物性对传热模型仿真精度的影响。

3 结果与讨论

3.1 计算结果与实验结果的比较

如图3所示，由这两种传热模型仿真所得的模具温度比其实测值都要偏高一些。主要原因是在实验中，电加热带的发热量总会有少部分会通过外表面的隔热层以及模具的两端散出去，致使实际的加热功率要比仿真计算所采用的名义加热功率低一些。另外还可以看出，第一种传热模型对模具温度的仿真精度要高于第二种传热模型。因为在第一种传热模型里，采用的是FLUENT软件中两相流的Mixture模型来进行仿真，即认为模具内部的混合物是由粉料和内部空气这两种流体均匀混合而成的。因此内部混合物与模具内壁面进行对流换热的强度比粉料处于实际的运动状态时要大，这样更多的热量就由模具传递给内部混合物，从而使得模具温度的计算值又会降低一些。即由第一种传热模型仿真所得的模具温度会更靠近实验结果一些，这样就抵消了一部分由于实验中加热功率损失所造成的模具温度的计算误差。

图3 模具温度的计算值与实测值的比较Fig.3 Comparison of calculated results with tested results for mold temperatures

在时间过了120 s后，模具的实测温度随时间增加的速率明显变缓。这是因为虽然此时模内温度还没有达到粉料的熔融温度，但靠近模具内壁面有少量粉料的温度已经升到了其熔融温度，并开始慢慢熔融。由于粉料熔融时发生相变会吸收大量的熔融潜热，因此使得模具自身吸收的热量比以前减少，温升也就显著变慢。但本文的传热模型研究的是在粉料开始熔融之前的加热过程，没有考虑相变吸热，因此模具温度的计算值随时间增加的速率并没有明显的变缓。根据图3所示模具温度的实测值随时间的变化规律，粉料开始熔融的时间应该在120～150 s之间。所以在时间过了150 s后，模具温度的计算值与实测值的误差开始急剧增大，这表明本文的传热模型已经不再适用于此后的加热过程。在150 s时，第一种传热模型对模具温度的仿真误差为7.3%，第二种传热模型对模具温度的仿真误差为12.1%。

如图4所示，由第一种传热模型计算所得的模内温度比实验结果偏高，而由第二种传热模型计算所得的模内温度比实验结果偏低。这两种传热模型计算所得的模内温度与实验结果的误差都是随着加热时间变得越来越大。如前所述，第一种传热模型高估了内部混合物与模具内壁面间的对流换热强度，致使更多的热量由模具传递给内部混合物，因此由第一种传热模型所得的模内温度计算值比实测值高一些。在150 s时，第一种传热模型对模内温度的仿真误差为13.5%，第二种传热模型对模内温度的仿真误差为19.5%。

图4 模内温度的计算值与实测值的比较Fig.4 Comparison of calculated results with tested results for internal temperatures

在第二种传热模型里，可能是由于采用式（5）计算所得的模具内壁面平均的传热系数hi不准确从而造成了模内温度的计算误差比较大。模具内壁面瞬时的传热系数随时间先急剧减小，然后减小的速率变缓，最后随时间趋于稳定[10]。式（5）中的平均传热系数hi是将瞬时传热系数在整个加热时间内进行积分，然后再除以加热时间得到的。但从模具受热到粉料刚开始熔融之间所花费的加热时间很难精确得出。在推导式（5）时所采用的加热时间可能比实际的加热时间要长，致使由式（5）算出的平均传热系数hi比实际值偏小。即低估了模具内壁面与内部混合物间的对流换热强度，从而使得由第二种传热模型得出的模内温度偏低，同时这也是造成该传热模型算出的模具温度偏高的另一个原因。实际上模具内壁面的传热系数受很多因素的影响，如模具的形状大小、加热的热流密度、粉料在模内空间的体积百分比、模具的转速等[11]。而式（5）只考虑了粉料在模内空间体积百分比的影响，没有考虑其他因素的影响，也会因此产生计算误差。

由以上分析比较可以看出，这两种传热模型对加热阶段的模具温度都具有足够的仿真精度，但对模内温度的仿真精度都不高，当然第一种传热模型相对要好一些。仿真精度主要取决于对模具内壁面与内部混合物的对流换热强度能否准确模拟。第一种传热模型的计算区域同时包括模具本身和内部混合物，因此在仿真时无需事先知道模具内壁面上的传热系数，而是通过把模具自身的导热与其内壁面和内部混合物间的对流换热耦合在一起来解决这个问题。而第二种传热模型的计算区域不包括内部混合物，因此必须已有准确的模具内壁面传热系数作为输入参数，否者无法得到精度较高的计算结果。但到目前为止还没有一个完善的理论公式或实验关联式可用来准确计算该传热系数。这就是第二种传热模型的仿真精度比第一种传热模型低的主要原因。但是从另一方面来讲，第一种传热模型由于需要仿真较为复杂的两相流问题，为保证叠代计算的稳定性和收敛性，所采用的时间步长很小，另外其仿真区域同时包括模具本身和模内空间，因此计算量非常大。而第二种传热模型只需求解简单的线性常微分方程组，计算量要小得多。

3.2 粉料物性参数的影响

严格来讲，在滚塑的加热阶段，粉料的物性参数如密度、热导率和定压比热容都会随着温度的升高而变化。粉料的定压比热容是指在压力恒定的条件下，单位质量的粉料的温度每升高1 K所需要吸收的热量。在以往的传热模型里，为减小仿真计算的难度，都是假设粉料具有常物性。如前所述，在图3和图4里的计算结果也是按照环境温度下的常物性仿真得到的。根据文献[12]的实验结果可知，在粉料开始熔融之前，其密度和热导率随温度变化很小。但定压比热容随温度变化很大，按照温度每升高1 K就增加16.4 J/kg•K的速率来变化。因此有必要分别采用本文的两种传热模型，将粉料的密度和热导率仍然当作常数，而将定压比热容随温度按照上述线性关系变化，重新进行计算以研究变物性对仿真精度的影响。

在图5和图6中分别给出了当考虑变物性时即定压比热容随温度增大时，由第一种模型仿真得出的模具温度和模内温度，并将其与假设常物性时的仿真结果以及相应的温度实测值分别进行了比较。可以看出在考虑变物性后，由第一种传热模型计算所得的模具温度和模内温度都比假设常物性时变低了一些，二者都更接近实验结果。这是因为随着加热过程的进行，由于粉料的定压比热容随粉料温度的升高而增大，即要让粉料产生温升则需要吸收更多的热量。但模具外壁面上的加热功率是不变的，因此考虑增大的定压比热容后，模具温度和模内温度的增速都会变缓，而且随着加热过程的进行，二者变缓的程度也越来越大。总的来说考虑了变物性后，第一种传热模型的仿真精度有所提高，尤其是当用来计算模内温度时，其仿真精度的改善更为明显。在150 s时，第一种传热模型对模具温度的仿真误差减小为4%，对模内温度的仿真误差减小为4.8%。

图5 第一种传热模型的模具温度的计算值与实测值的比较Fig.5 Comparison of calculated results by the first model with tested results for mold temperatures

图6 第一种传热模型的模内温度的计算值与实测值的比较Fig.6 Comparison of calculated results by the first model with tested results for internal temperatures

由图6还可以看出，在120 s后，第一种传热模型仿真所得的模内温度由以前的高于实验结果变成了低于实验结果。一方面由于粉料的定压比热容随粉料温度的升高而增大，致使仿真所得的模内温度升高的速率低于假设常物性时的情形。另一方面在120 s后，有少量的粉料逐渐开始熔融。由实验结果看出，此时模具温度升高的速率明显降低，这意味着有更多的热量由模具传递给了内部混合物。这些多出来的热量一部分用于粉料的熔融相变吸热，另一部分则用于模内温度的继续升高。由于在120～180 s这一段时间里，开始熔融的粉料还比较少，因此前述第一部分热量所占的比例还不大，而第二部分热量所占的比例比较大，从而使得实际的模内温度快速升高，就造成了此后模内温度的实测值变得高于计算值。

在图7和图8中分别给出了当考虑变物性时即定压比热容随温度增大时，由第二种传热模型仿真得出的模具温度和模内温度，并将其与假设常物性时的仿真结果以及相应的温度实测值分别进行了比较。结果发现考虑变物性后，采用第二种模型几乎没有改善模具温度的计算精度，但在加热时间90 s后反而会使得模内温度的计算精度明显变差。这个变差的原因可能还是由于所采用的模具内壁面与内部混合物间的传热系数不准确造成的。

图7 第二种传热模型的模具温度的计算值与实测值的比较Fig.7 Comparison of calculated results by the second model with tested results for mold temperatures

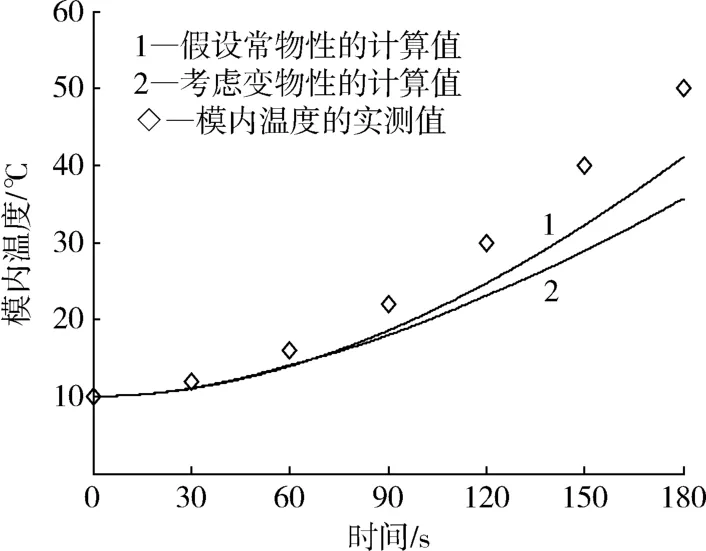
图8 第二种传热模型的模内温度的计算值与实测值的比较Fig.8 Comparison of calculated results by the second model with tested results for internal temperatures

由以上分析可以看出，除非预先能获得比较准确的模具内壁面上的平均传热系数，否则第二种传热模型对模内温度的仿真误差比较大，而且随着加热过程的进行，这个误差变得越来越大。但是如前所述，第二种传热模型对模具温度的仿真误差还是可以接受的，这主要是因为模具温度受内壁面上传热系数的影响程度不像模内温度那么大。当模具温度升高到粉料的熔融温度时，可以认为模内的粉料开始熔融了。即准确地仿真模具温度也就意味着可以准确地预测加热时间。考虑到第二种传热模型的计算量比第一种传热模型小很多，因此采用第二种模型来仿真模具温度和预测加热时间就具有极大的优势。但如果需要较为准确地仿真模内温度，则还是应该采用计算量更大、更复杂的第一种传热模型。

4 结论

（1）两种传热模型对模具温度的仿真精度都比对模内温度的仿真精度要高；无论是用于仿真模具温度还是模内温度，第一种传热模型的精度都要高于第二种传热模型，但前者的计算量要远远大于后者的计算量；

（2）当考虑变物性时，第一种传热模型的仿真精度有所改善，尤其是对模内温度的仿真精度改善更为显著；第二种传热模型对模具温度的仿真精度几乎没有改善，对模内温度的仿真精度反而变得更差；

（3）综合来看，第二种传热模型在计算模具温度时具有一定的优势，但不适用于计算模内温度；而第一种传热模型，尤其是在考虑变物性的情况下，更适用于计算模内温度。