与参考答案不一样的正确答案
——由非独立变量引发的问题
王美芳
(复旦大学附属中学 上海 200433)
1 是我做错了吗
有个学生告诉我他做了今年的青浦物理二模卷最后一题的最后一小题,用了自己的方法,得到了一个跟参考答案完全不一样的解,他自己找不出问题在哪里,希望我帮他看一看.我看了他的解法,是利用牛顿第二定律,积分求解的.他提供的计算过程有些错误的地方,我帮他修正后得到的解依然是不同于参考答案的.这个事情比较有意思,所以和大家分享一下.
【题目】如图1(a)所示,在竖直平面内平行放置了两根完全相同的金属导轨,间距为L=0.2 m.其中a1b1段和a2b2段是竖直放置的足够长的光滑直轨道;b1c1和b2c2段是半径为R=0.25 m的光滑圆弧轨道,圆心角为127°,圆心O1和O2与b1和b2在同一高度;c1d1和c2d2段是粗糙的倾斜直轨道,与水平面成37°角放置,轨道长度足够长.图1(b)是其正面视图.a1a2之间连接一阻值为R0=0.5 Ω的电阻.现有一质量为m=0.1 kg,电阻为r=0.5 Ω的金属棒通过两端的小环套在两根轨道上,棒与轨道的c1d1和c2d2段之间的动摩擦因数为μ=0.25.棒从倾斜轨道上距离c1c2为s=2 m处由静止释放,在棒到达b1b2瞬间,在竖直轨道区域内出现水平向右的匀强磁场,磁感应强度为B=0.5 T,运动中棒始终与导轨垂直.(sin 37°=0.6,cos 37°=0.8,g=10 m/s2)
(1)求棒在倾斜轨道上运动的时间t1;
(2)求棒到达b1b2处时R0的电功率P0;
(3)请分析说明棒在磁场区域运动的情况;
(4)若棒刚越过b1b2处时的速度设为v1,在磁场内运动的时间设为t2,求棒刚离开磁场区域时的速度v2.
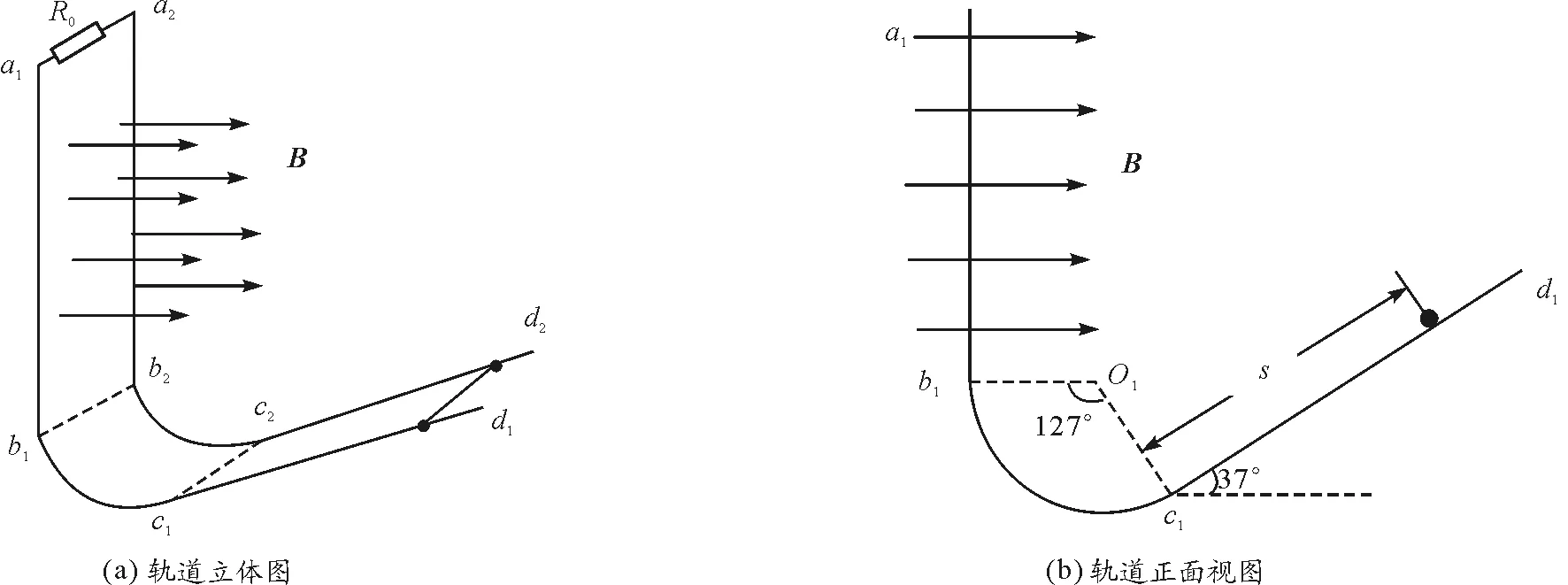
图1 题目题图
其中第(4)小题独立于前面3个小题,所以这里跳过前面3小题,直接讨论第(4)小题.第(4)小题的参考答案是v2=gt2-v1,下面给出两种不同的解法.
(1)微元累加解法
先给出常规的微元累加的解法:
以竖直向下为正,由牛顿第二定律得
经过一小段时间Δt
考虑在磁场中的整个运动过程,对时间分割,再微元累加得
整个过程,时间为t2,位移为零,速度的变化量为v2-(-v1),注意:进入磁场的初速度为-v1(在本题中,已知条件中的v1是初速度的大小部分,实际满足以上公式的初速度应为-v1),所以有
∑Δt=t2
∑vΔt=0
∑aΔt=v2-(-v1)
联立得
(2)积分解法
再来看另一种解法:
由牛顿第二定律得
mg+F安=ma
以竖直向下为正,则
两边分别积分
由此得t2时刻对应速度v2
(1)
于是,这里我们看到了两种解,放在一起对比一下
这里积分求解得到的答案看着比较复杂,和参考答案形式上很不一样,那么,它错了吗?
2 两个答案等价性证明
对积分求解继续深入,可得到s(t),令s(t)=0,得到在磁场中的运动时间t2满足的关系式,代回v2的积分求解表达式,可证明两个答案的等价性.
(1)写出s(t)
(2)给出磁场中运动的时间t2满足的表达式
令s=0,对应的t有两个解,t1=0,即刚进入磁场位移为零,另一解t2应对应出磁场时刻,所以t2满足
整理得t2满足
(2)
(3)证明两种解的等价性
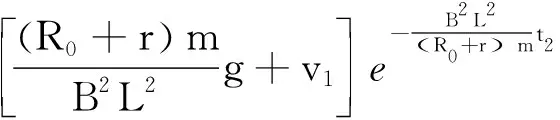
两个解的等价性得证.所以,式(1)虽然形式与参考答案不同,也是本题的一个正确答案.
3 反思
为什么会有两个看似不同的正确答案?问题的关键是本题中,在磁场中的运动时间t2不是一个独立变量.从刚才的证明中可以看出,t2是可以根据已知条件求得.这就导致了本题v2的表达形式不唯一.
实际上,由于题目中给定的物理量不是独立变量,造成答案不唯一情况并非只有这一个例.2008年江苏物理高考最后一题类似于这种情况[1],学生有可能会给出不用于参考答案的另一个正确答案,原因就是题目中给的已知量并非全部独立变量.
对我们教师来说,由此得到的经验应该是:在电磁感应计算题的命题过程中要做好设计探析[2],其中就要注意考虑到独立变量问题.如果题目中出现类似情况,对做出其他解而感觉迷惑的学生应加以鼓励并对其解分析解释.在注重物理核心素养培养的背景下,更应注意培养学生的质疑精神和发散性思维,不能因为和参考答案不一致而武断地判定学生解答错误.

