对堆叠物体保持直立下落条件的探究*

蔡忠琴 邓荣萍 佘欣芮 王龙军

(西南大学物理科学与技术学院 重庆 400715)

1 引言

本实验基于IYPT2020“下落的塔”一题.相同的物体彼此堆叠，形成独立的塔，通过施加突然的水平力来卸下底部物体，以使塔架的其余部分下降到地面上，并且塔架保持直立.在日常生活中也有类似的现象，例如，将多枚象棋叠放形成“高塔”，当快速击打最下方的象棋时，在一定条件下，上方象棋能够保持直立下落.为研究该现象并确定允许塔保持直立下落的条件，我们设计了以下方案进行实验和探究.

2 实验方案一

2.1 实验原理

底块在突然的水平力和摩擦力的作用下开始向前近似做匀减速直线运动.对于这个突然的水平力，其作用效果可以等价为给底块施加一个突然的速度.当底块抽出后的末速度刚好为零且下落的塔能保持稳定时，此时施加的初速度即为塔保持稳定对应的最小初速度.在理论推导和实验中，我们将塔的稳定性转化为对最小初速度的探究，而后又将该最小初速度经实验方案的设计转化为对最低高度的探究.

2.1.1 倒塌条件

倒塌条件分析示意图如图1所示.

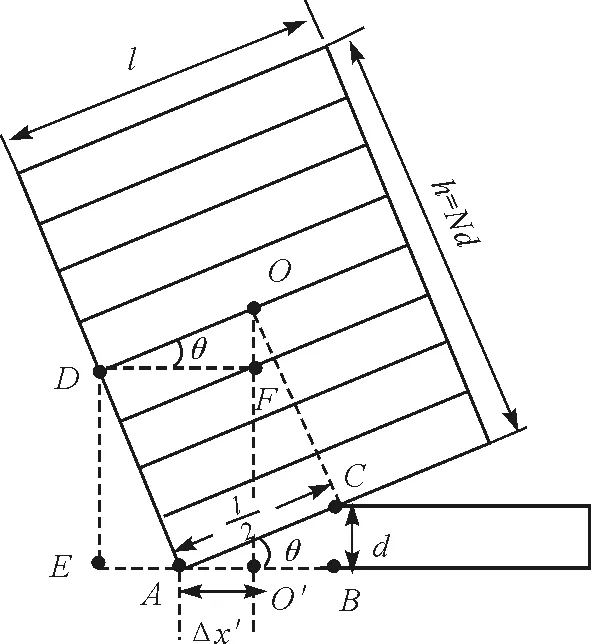
图1 倒塌条件分析示意图

对三角形ABC

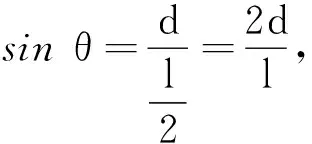
(1)

由 △ODF≌△ABC，则

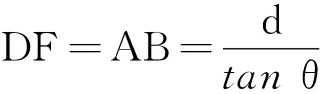
在△ADE中

则塔的重力作用线与塔的边缘点之间的水平距离

Δx′=EO′-AE=DF-AE=

(2)

图1中，Δx′=0，重力作用线过支点A,处于临界状态，当Δx′<0时，塔的重力作用线位于A点左侧，则塔在重力作用下会倒塌.

2.1.2 最低高度的理论推导

为给底块提供突然的初速度，可让与底块相连且规格一致的重物从一定高度处自由下落.最低高度的理论推导示意图如图2所示.

图2 最低高度理论推导示意图

重物的重力势能转换为动能.理想情况下，绳绷直时，可认为重物与底块发生完全弹性碰撞，则重物与底块将进行速度交换.

对底块，由牛顿第二运动定律，其加速度

(3)

其中μ1为底块与底板之间的摩擦因数，μ2为物块之间的摩擦因数，M为塔的总质量,m为底块质量.

同理，塔的整体加速度

a2=μ2g

(4)

对底块进行运动分析，假设其末速度恰好为零，由v0=a1t，则

(5)

设底部物块的位移为x1，塔在抽出过程中产生的位移为x2，Δx为其相对位移.

对塔进行运动分析如下

(6)

底块恰好被抽出后

Δx=x1-x2=l

(7)

联立式(3)～(7)得

(8)

代入相应数据，则可以算出塔在抽出底块后仍保持稳定时对应的最低高度.

当组成塔的单个物块的质量与底块的质量以及重物的质量相等时，可以得到更理想的最低高度，即

(9)

其中N为组成塔的物块个数.从该式可以看出，在单个物块质量与底块质量及重物质量相等条件下，最低高度h与单个物块的质量m无关.

2.2 实验装置

实验器材：若干方形小木块、亚克力板、夹子、铁架台、定滑轮、细线.实验装置安装示意图如图3所示.

图3 方案一实验装置安装示意图

2.3 实验内容

将亚克力板和滑轮固定在支架上，底块与重物用细线相连，调整滑轮位置，使细线拉直时与底块的重心在同一条直线上.将方块整齐堆叠在亚克力板上.调节夹子高度，使重物从不同高度落下.塔从3块方块开始实验(N=3).调整重物高度，测出使底块刚好抽出而塔不倒对应的最低高度，将其记录在表格中.逐个增加塔的块数，重复以上操作，最后作出理论和实验的最低高度的趋势曲线进行观察比较.

2.4 实验结果

得出各块数对应的最低理论高度，与实验值进行对比，实验数据与理论数据见表1，实验高度与理论高度拟合曲线如图4所示.

表1 实验数据与理论数据记录表

图4中，横轴为塔的块数N，纵轴为下落高度h.由图4可知，实验和理论基本相符.此外，在实验过程中，可以定性得出最小初速度越大，塔的稳定性越高，即突然的水平力越大，塔越稳定的初步结论.

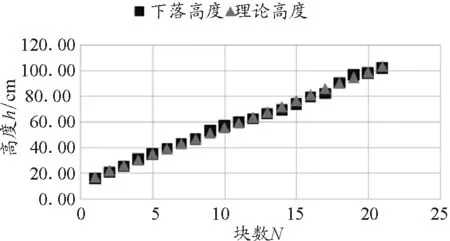
图4 实验高度与理论高度拟合

为研究塔在倒塌过程中更细节的过程，我们设计了更严谨的方案二进行实验和探究.

3 实验方案二

3.1 实验原理

设塔与底块由N+1个圆块组成，从下到上编号依次为0,1,…,N.设定参数如下：m为圆块质量、g为重力加速度、r为圆块半径、μ0为圆块与底板之间的摩擦因数、μ1为圆块之间的摩擦因数、F为施加的作用力、h为圆块厚度、xi为第i个圆块的位移.

对理想模型，当底块向右运动时，上面的塔会受到支持力、重力及向右的摩擦力的作用，可分为以下3个过程进行讨论.

过程一：抽离

对底块

(10)

同理对于其余圆块有

……

(11)

上式中的fN,fN-1,fN-2,…,f1,分别表示相邻两物块之间的静摩擦力大小.由此可得，底块以上的部分从理论上可以真正看作一个整体.且只有当

F>μ0(N+1)mg+μ1Nmg

(12)

时，底块才开始被抽离.

过程二：转动

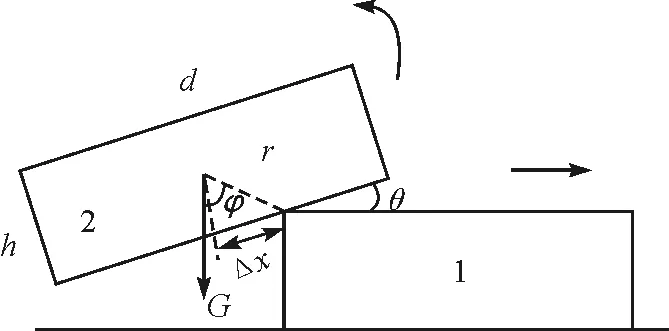
图5 转动分析示意图

根据刚体力学中的转动定律

r×F=Jα

(13)

代入数据得

(14)

由边角关系得

(15)

计算转动惯量

(16)

则得关系式

(17)

由此可知，塔的转动角度与塔的总质量、总高度以及物块的直径有关[1].

设底块与塔座恰好完全分离时塔转过的角度为θ1，分离示意图如图6所示.此时若塔的重力作用线越超过塔座左边缘位置B而位于其左边时，则塔会倒塌[2,3].具体分析如下：

图6 塔与底块分离示意图

由图可知，重心与塔座左边缘处的水平距离

O′B=O′A-AB=CD-AB

又由边角关系

(18)

当O′B>0时，塔会倒塌.

过程三：下落

(19)

同理，当O′B>0时，塔会倒塌.

3.2 实验装置

实验器材：不同规格的圆块若干,2～4 g质量不等的小铁球若干,定滑轮、电磁铁、亚克力板、学生电源、开关、小布袋、细线.

实验装置安装示意图如图7所示.

图7 方案二实验装置示意图

3.3 实验内容

3.3.1 实验设计

设计两组实验如下：

在探究圆块厚度与塔稳定性的关系时，选用30 cm×5 cm,30 cm×8 cm,30 cm×10 cm这3种规格的圆块进行实验；探究圆块直径与塔稳定性的关系时，选用30 cm×10 cm,40 cm×10 cm,50 cm×10 cm这3种规格的圆块进行实验.

3.3.2 实验操作

将亚克力板和滑轮固定，将底块与装有铁球的布袋用细线相连，调整滑轮位置，使细线拉直时与底部物块的重心在同一条直线上.将圆块整齐堆叠在亚克力板上.通过断开电磁铁的开关，突然释放装有铁球的布袋，释放瞬间通过细绳对底块施加一个突然的水平力.通过改变布袋里铁球的个数来改变水平力的大小.

从3块圆块开始实验.调整布袋中铁球的总质量，测量出使底块刚好抽出而塔不倒时布袋中铁球的总质量，将其记录在表格中.

逐个增加圆块个数，重复以上操作.

最后作出相应的趋势曲线进行观察比较，得到一般结论.

3.3.3 数据记录

实验数据记录如表2所示.

表2 不同规格和块数的塔对应的铁球质量记录表

由以上实验数据可得圆块厚度相同、直径不同时稳定情况如图8所示；圆块直径相同、厚度不同时稳定情况如图9所示.

3.4 实验结果

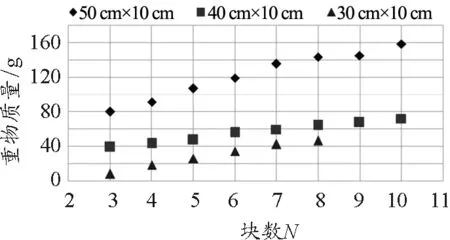
图8 厚度相同、直径不同时数据处理图

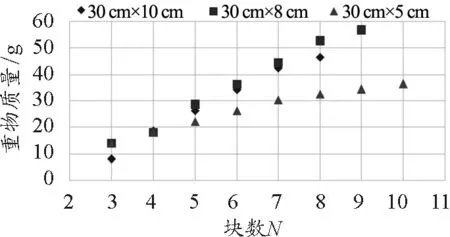
图9 直径相同、厚度不同时数据处理图

从实验结果可以看出，圆块厚度相同时，半径越大抽出底块而塔不倒塌所需的铁球质量越大，即证明其稳定性越高；圆块直径相同时，在误差范围内可以得出，圆块厚度越小，塔越稳定，且堆叠块数越多现象越明显.

4 结论

从以上两个实验方案可知，影响堆叠物体保持直立下落的条件有水平力的大小、物体的规格、块数、高度等，通过实验可得到一般结论如下：

(1)其他条件一定时，抽出底块的最小速度越大，塔越稳定；即水平方向上突然施加的力越大塔越稳定.

(2)其他条件一定时，组成塔的块数越多，塔越不稳定.

(3)其他条件一定时，圆块的半径越大，塔越稳定.

(4)其他条件一定时，圆块的高度越小，塔越稳定.