一种全新的物理计算工具
——计算地图
谌华生
(随县小林镇中心学校 湖北 随州 441300)
1 什么是计算地图
2017年,笔者主讲了复习课“浮力相关计算中的一般思路”,旨在帮助学生理清浮力计算中常见的几条思路,如M→v→v排M排→G排→F浮等,以提高学生浮力相关的计算能力.在课后反思中,发现可以把几条线路(即思路)拼接起来,且拼接起来的图形可以帮助学生快速找到解题思路,就如同生活中的交通地图能为出行的人们提供导航一样.鉴于没有描述这种图形的相关概念,笔者把这种图形命名为“物理计算地图”.如图1和图2所示,分别为“平均速度计算模型”和“浮力之一般计算模型”的计算地图.这种能清晰、完整地反映某物理模型中各个物理量之间数理和逻辑关系的特殊图形,叫做计算地图.
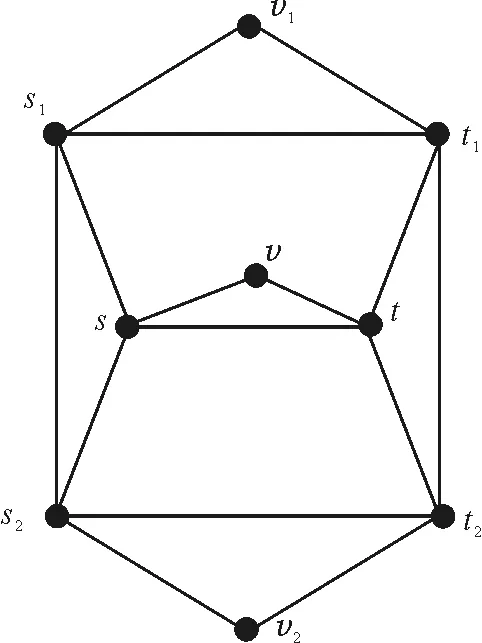
图1 平均速度计算模型
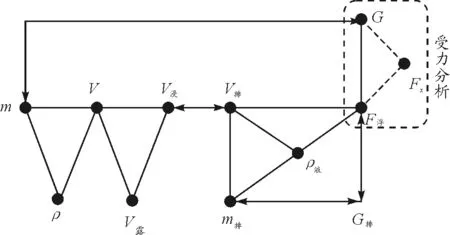
图2 浮力之一般计算模型
下面以“平均速度计算模型”的计算地图图1为例,说明计算地图的绘制过程及使用方法.该模型往往把物体的运动过程分为:速度分别为v1和v2,时间为t1和t2,路程为s1和s2的两段,而全程的平均速度,时间和路程分别用v,t和s表示,共9个物理量,用 9个点表示.3个有数理或逻辑关系的物理量拼接成一个三角形,分别把5个关系式s1=v1t1,s2=v2t2,s=s1+s2,t=t1+t2,s=vt所代表的三角形再拼接成一个大图,就形成了图1.使用时,知道一个三角形上的任两个顶点就可以行进到第三个顶点,结合其他已知量,就可以一步一步地向前行进,直至到达待求量.
2 计算地图有什么用
计算地图为计算而生,它能为计算导航,就如同生活中的各种交通地图能为人们的日常出行导航一样.在具体的物理计算问题中,计算地图能帮助解题者快速发现所要求解问题的思路,从而顺利地解答问题.下面举例说明.
【例题】如图3所示,用弹簧测力计在空气中测得某物体重8.9 N,将该物体浸没在水中,弹簧测力计的示数变为7.9 N.求该物体的密度.(取g=10 N/kg)

图3 例题题图
分析:这是一道经典浮力计算题,对应的计算地图为上述的图2.题目明确给出的条件有两个,一个是物体的重力G=8.9 N,而条件“弹簧测力计的示数变为7.9 N”告诉我们,此时物体受到弹簧测力计对它竖直向上的拉力为7.9 N,即告诉我们地图中的外力“Fx”为7.9 N,我们可以结合题意,用“F拉”替代“Fx”,即题目的另一个条件是物体受到竖直向上的拉力F拉=7.9 N.结合题目的描述,我们不难发现题目还间接告诉我们另外两个隐含条件:一个是液体的密度ρ水=1.0×103kg/m3;一个是物体被浸没,表示为V露=0,也可以说成是它的推导结论为V排=V.所以,题目共给出4个条件,下面我们在地图中分别圈出已知量与待求量,其中实线圆圈所圈注的物理量代表已知量,虚线圆圈所圈注的物理量代表待求量,如图4所示.
图5所示计算地图中,待求量ρ处在一个三角形之中,并且该三角形中的另两个顶点所代表的物理量m和V未知,所以,必须要先求出物体的质量m和体积V.观察地图,我们很直观地就能找出计算求解物体质量m的思路为红色细箭头所标示的线路①;接着就可以根据黑色粗箭头所标示的线路②求出待求量ρ.线路①和线路②分别对应图5中的两条红细、黑粗线路.

图5 所确定的解题线路即解题思路
(1)首先根据地图中的“G→m”线路①,求出物体的质量m,如图6所示.

图6 线路①
(2)接着根据地图中的“G,Fx→F浮→V排→V浸→V→ρ”线路②,先求出物体的体积V(图7).
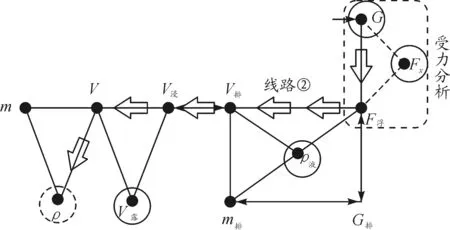
图7 线路②
最后利用密度ρ所在的局部三角形地图,结合刚求出的物体的质量m,可求出物体的密度ρ.
本题的详细求解过程如下.
解:物体的质量为
分析物体的受力如图8所示(F浮、F拉两力的示意图已平移),则有平衡方程
G=F浮+F拉
所以,物体所受浮力
F浮=G-F拉= 8.9 N - 7.9 N = 1 N
由阿基米德原理F浮=ρ液gV排得
1×10-4m3= 100 cm3

图8 物体受力示意图
又因为浸没,所以,V=V排= 100 cm3,则物体的密度为
求毕.
上述例题是一道经典浮力计算题,难度适中,对于一般的初中生来说,还是很有挑战性的.但如果借助上面的计算地图,情况就不一样了,物理计算就像是在玩游戏,绝大多数学生在很短的时间内就可以确定出解题思路,并能独立、顺利地求解出最终的问题.可见,计算地图作为一种全新的辅助物理计算工具,它是真的能为物理计算导航.
3 计算地图为什么能为物理计算导航
在传统的计算过程中,学生大脑回忆的是相关公式,看不到所有物理量间逻辑关系的全貌.“不识庐山真面目,只缘身在此山中”,他们当然很难找到解题的思路.而计算地图所呈现的是所有物理量间的所有逻辑关系的全貌或整体,它使思维变得可视化,可轻易从计算地图中找到解题思路,为物理计算导航.
计算地图把某种物理模型中各个物理量间的逻辑关系清晰、完整地呈现在我们的眼前,所以,物理量与物理量间的关系一目了然.题目中的已知物理量(常被称为“已知条件”)类似于始发地,待求物理量类似于目的地,所以对照计算地图就可以直观地找出从已知物理量到待求物理量间的线路即解题思路,根本不需要冥思苦想.接下来,只需按照解题思路,先后计算出必要的中间物理量(类似于日常出行时要经过的中间站点),直至最终求解出待求的物理量.
从上述例题的求解过程可以发现,运用计算地图解题的步骤共有3步:
首先,通过审题弄清题目的已知量与待求量,并在计算地图中分别圈出已知量与待求量,相当于明确自己的位置在哪里;
然后,观察计算地图,寻找并确定已知量与待求量之间的可行线路,即确定解题的思路;
最后,按照既定的思路,一步一步地计算求解,直至最终求解出待求量,简单而完美.
4 如何绘制计算地图
那么如何绘制计算地图呢?或者说优秀的计算地图的标准是什么呢?笔者认为,绘制计算地图应遵循以下几个原则:
(1)对应性.没有一个可用于所有计算题的万能地图,所谓的计算地图都是针对某一物理情境或某一计算模型来说的.所以,计算地图必须与某一类型的计算模型对应,这就是计算地图的对应性或一致性.用交通地图类比,北京市有北京市的交通地图,湖北省有湖北省的交通地图,没有一张既可适用于北京又可适用于湖北省的交通地图.
(2)科学性.计算地图的绘制会受到个人因素的影响,不同的人针对同一个计算模型所画出的计算地图的外形不尽相同.但这种不同一定是微小的、局部的.计算地图要从根本上反映相关计算模型中各个物理量间的逻辑关系,这种关系是众多物理概念和规律的反映,它是客观存在的,也是稳定的,更是不以人的意志改变的.某两个物理量间到底有没有通路,不是你我能决定的,而是决定于实际的问题情境和已总结出的物理规律.所以,所绘制出的计算地图要符合科学规律,而不能人为的臆造,这就是计算地图的科学性.图9这个计算地图其实与图1没有什么两样,你把它旋转任何角度,它们间的关系也不会受到丝毫影响.
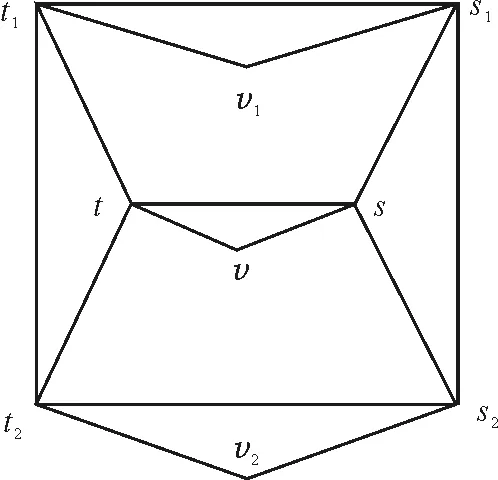
图9 平均速度计算的另一种计算地图
(3)完整性.在叙述“对应性”时说道,某一个计算地图是针对某一物理情境或某一计算模型来说的,计算地图要与某一类型的计算模型对应.在一个具体的物理问题情境中,到底涉及哪些物理量,又有哪些物理量间存在着一定的数量逻辑关系,这取决于问题本身.也就是说,在一个具体的物理问题情境中,涉及的物理量的个数是一定的,物理量间的数量逻辑关系或关系式的数量也是一定的,如在平均速度计算模型中,存在的物理量分别是:
s1——物体所通过的第一段路程;
t1——物体通过第一段路程所用的时间;
v1——物体通过第一段路程的速度;
s2——物体所通过的第二段路程;
t2——物体通过第二段路程所用的时间;
v2——物体通过第二段路程的速度;
s——物体所通过的整段路程即全程;
t——物体通过整段路程所用的时间;
v——物体通过整段路程的速度;
共9个.
这9个物理量中,存在的关系式有
s1=v1t1
s2=v2t2
s=s1+s2
t=t1+t2
s=vt
共5个.
所谓平均速度计算模型对应的计算地图,本质上就是用5个关系式来表示这9个物理量间的逻辑关系图.所以,在一个计算地图中,少一个物理量或少一个关系式,都是不全面的,这就是计算地图的完整性,即计算地图要完整地反映某物理模型中各个物理量之间逻辑关系.如果在绘制地图的过程中,某两个物理量的关系没有反映出来,那么这样的计算地图就不能很好地为我们导航.试想一下,如果在一个地区的交通地图中,少了一个重要的地点,或少了一条重要的交通路线,那么我们就可能远离最理想的出行线路.
(4)简洁性.好的东西总让人觉得简单,给人方便.同样地,完美的计算地图,也一定是清晰的、简单的.在计算地图的绘制过程中,各个物理量的位置摆放在哪里,线条如何勾画,都影响着地图的整体效果.有时可能会涉及较多的物理量,而物理量间的关系又很复杂,如某一个物理量与众多其他物理量间都存在着逻辑关系,这时,仅用平面图形表示可能会导致线条多且交叉,这样绘制出来的计算地图中的物理量间的关系就会显得杂乱无章、模糊不清,从而失去计算地图的意义.图10和图11,都是针对“欧姆定律之串联电路模型”所绘制的计算地图,但地图的整体效果相差很大.图11是用立体图形来呈现各个物理量间的关系,我们可以看到,地图中线条交叉的不多,图中各种关系呈现得很清晰,各种关系一目了然,使用这种更加简洁的地图能够帮助解题者更快地找到解题的思路.

图10 欧姆定律之串联电路模型(第1种)

图11 欧姆定律之串联电路模型(第2种)
作为一种全新、高效的物理计算辅助工具,计算地图将倍受关注,它的出现或许会打破“物理难学”的尴尬局面.

