燃料电池用交错并联型Boost变换器参数综合设计方法

马小勇 王议锋 王 萍 孟 准

燃料电池用交错并联型Boost变换器参数综合设计方法

马小勇1王议锋1王 萍1孟 准2

（1. 天津大学智能电网教育部重点实验室 天津 300072 2. 国网天津市电力公司经济技术研究院 天津 300171）

以燃料电池用交错并联型Boost变换器为研究对象，该文提出一种兼顾效率与功率密度的参数综合设计方法。首先对比单支路运行和多支路交错运行的电压及电流纹波，引入纹波抑制比量化交错并联对纹波的影响，从而建立变换器整体纹波要求与支路参数的对应关系，以此为基础进行参数设计。在参数设计过程中，以开关频率s、电感电流纹波DI以及电感磁心半径为自变量，进行损耗建模和无源器件体积建模。以变换器损耗小于设定值为约束条件，以无源元件体积和最小为目标，优选最佳参数。在此基础上，进行电容取值和电感设计，进而实现兼顾效率和功率密度的设计目标。最后，通过仿真及搭建40kW实验样机，验证了理论分析的正确性和参数设计方法的可行性。

燃料电池 交错并联 Boost变换器 参数设计和优化

0 引言

随着化石燃料短缺和环境问题的日益严重，燃料电池电动汽车（Fuel Cell Electrical Vehicles, FCEV）因其清洁无污染、能量转换效率高、燃料加注便捷、无续航里程焦虑等优势[1-3]，受到了国内外学者的广泛关注。

随着输出功率的增大，燃料电池的输出电压下降明显[4-5]，不利于行车安全。此外，燃料电池对电流纹波非常敏感，过大的电流纹波会对电池的质子交换膜产生不可逆转的损害，从而缩短电池寿命。

交错并联型Boost DC-DC变换器因其结构简单、成本低、效率高等优势在燃料电池电动汽车中得到了广泛应用[6-7]。在交错并联Boost变换器中，多个Boost支路并联，总电流应力被均分在各支路上，这不仅提高了变换器效率，还便于器件选型和降低成本[8]。此外，由于各支路交错运行，支路电感电流纹波在输入侧相互抑制，从而有助于减小输入电流纹波[9-10]。

车载场景下对变换器的体积和效率均提出了较高的要求。因此，燃料电池电动车用交错并联型Boost变换器必须具备高效率和高功率密度的特点。文献[11-13]提出将耦合电感应用于燃料电池电动车中，不仅减小了电感的体积和电流纹波，还能提高变换器效率。然而耦合电感的设计难度和成本随变换器功率的增大明显增加。文献[14-15]针对燃料电池应用场景，在交错并联Boost变换器的基础上，提出了多器件交错并联拓扑结构，以进一步降低输入电流纹波，减小电感的体积，从而提高变换器的效率和功率密度。然而，多器件交错并联拓扑存在器件并联均流问题，且驱动电路复杂、成本较高。此外，上述研究未能量化效率和功率密度之间的关系，故不能系统性地优化变换器参数，以实现兼顾效率和功率密度的参数最优设计。考虑到车载场景下对变换器效率和功率密度的高要求，进行兼顾效率和功率密度的参数综合设计研究具有重要的工程意义，这也是本文的研究重点。文献[16-18]针对交错并联型Boost功率因数校正（Power Factor Cor- rection, PFC）提出了兼顾效率和功率密度的参数设计方法，可为燃料电池用交错并联型Boost变换器的参数综合设计问题提供参考。

本文以燃料电池用交错并联型Boost变换器为研究对象，提出了一种兼顾效率与功率密度的参数综合设计方法。先量化交错并联结构对纹波的影响，在此基础上建立变换器整体纹波要求与支路参数设计的对应关系，进而指导变换器参数设计。由于开关频率s、电感电流纹波D以及电感磁心半径三者无耦合关系，在参数设计过程中，将其作为自变量进行损耗建模和无源器件体积建模。以变换器损耗小于设定值为约束条件，以无源元件体积和最小为目标，优选最佳参数。在此基础上，进行电容取值和电感设计，从而实现兼顾效率和功率密度的设计目标。本文通过仿真及搭建40kW实验样机，验证理论分析的正确性和参数设计方法的可行性。

1 拓扑和工作原理

6路交错并联型Boost变换器拓扑如图1所示。图中，1～6为各Boost支路电感，S1～S12为MOSFET，o为输出电容，in为输入电容，L为负载，此外各升压支路参数一致。由于并联分流作用，支路电流应力为总电流应力的1/6。考虑到燃料电池对电流纹波非常敏感，为减小输入电流纹波，延长电池使用寿命，加入输入电容in。

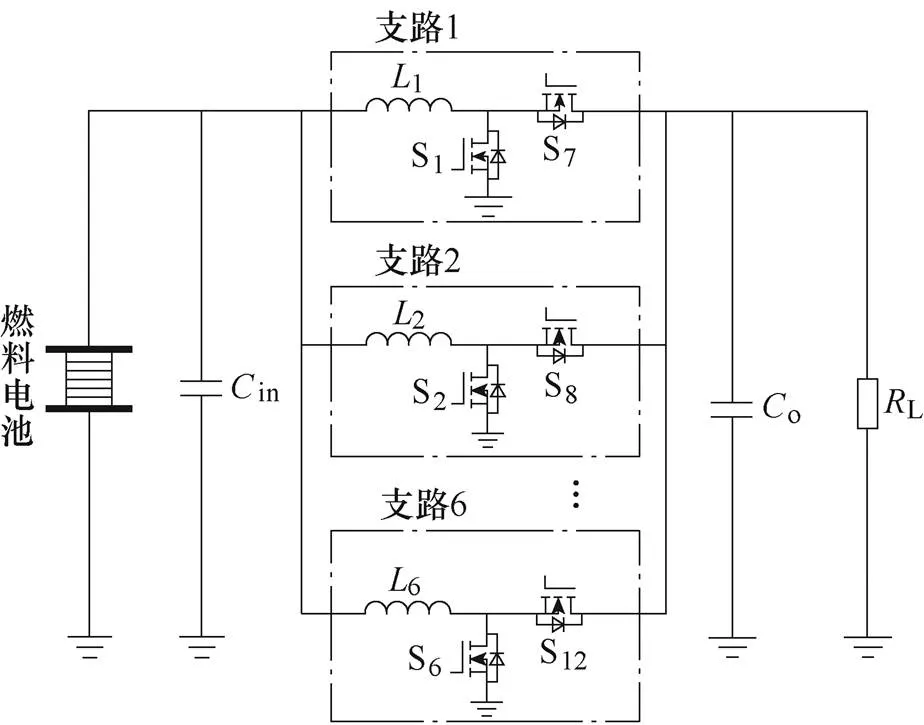
图1 6路交错并联型Boost变换器拓扑

驱动信号及电流纹波关系如图2所示。驱动信号周期为s，电感工作于电流连续导通模式（Con- tinous Conduction Mode, CCM），驱动信号如图2a所示。图中，S1～S6为Boost电路主开关，驱动信号相互交错，相位差为60°；S7～S12为同步整流管，其驱动信号与各自的主开关相位相反，两者间存在死区。

1～6为对应各支路的电感电流，交错并联后总电感电流t与支路电感电流的关系如图2b所示。由图可知，交错并联后，总电感电流纹波得到抑制，且其频率提高至开关频率s的6倍。

变换器用于燃料电池电动汽车，其设计参数见表1。由表1可知，变换器具有大功率、低纹波及高效率的设计要求。为满足纹波和效率要求，需对开关频率s、电感、输入电容in和输出电容o的取值进行综合设计。在参数设计过程中，应保证最佳功率密度以适应车载场景。

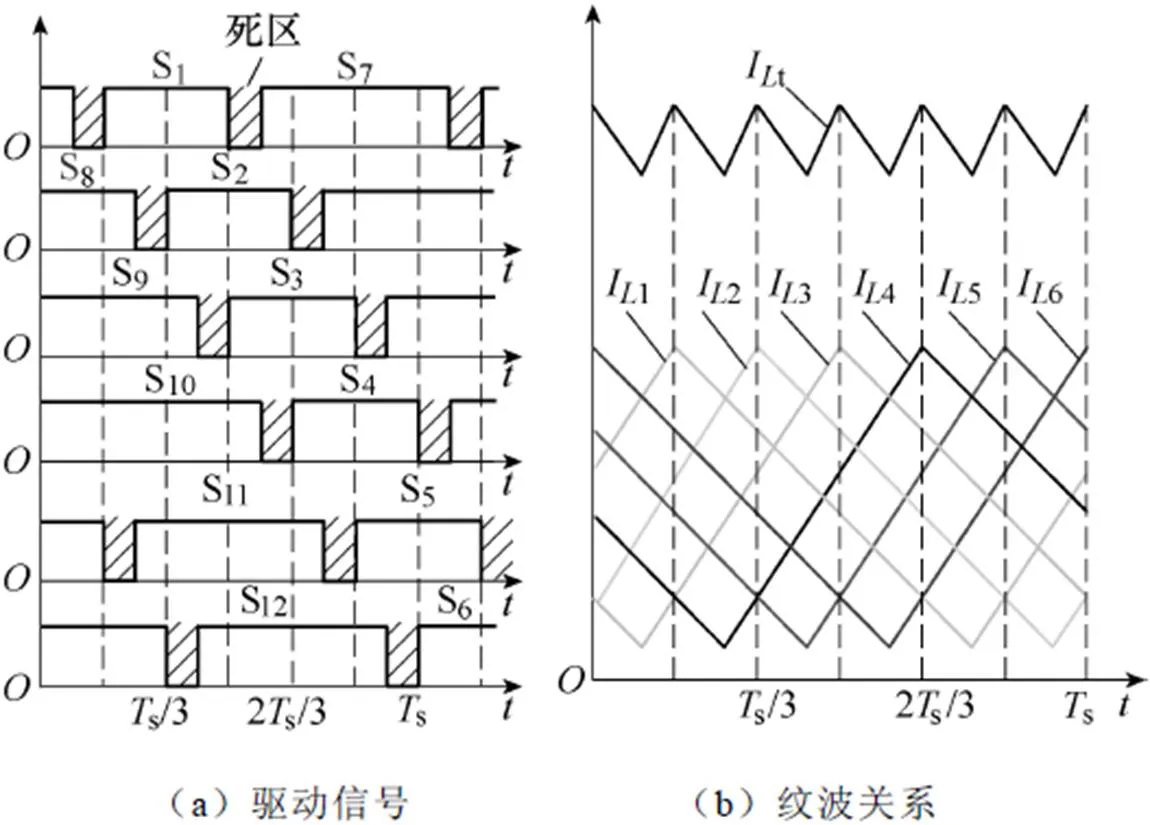
图2 驱动信号及电流纹波关系

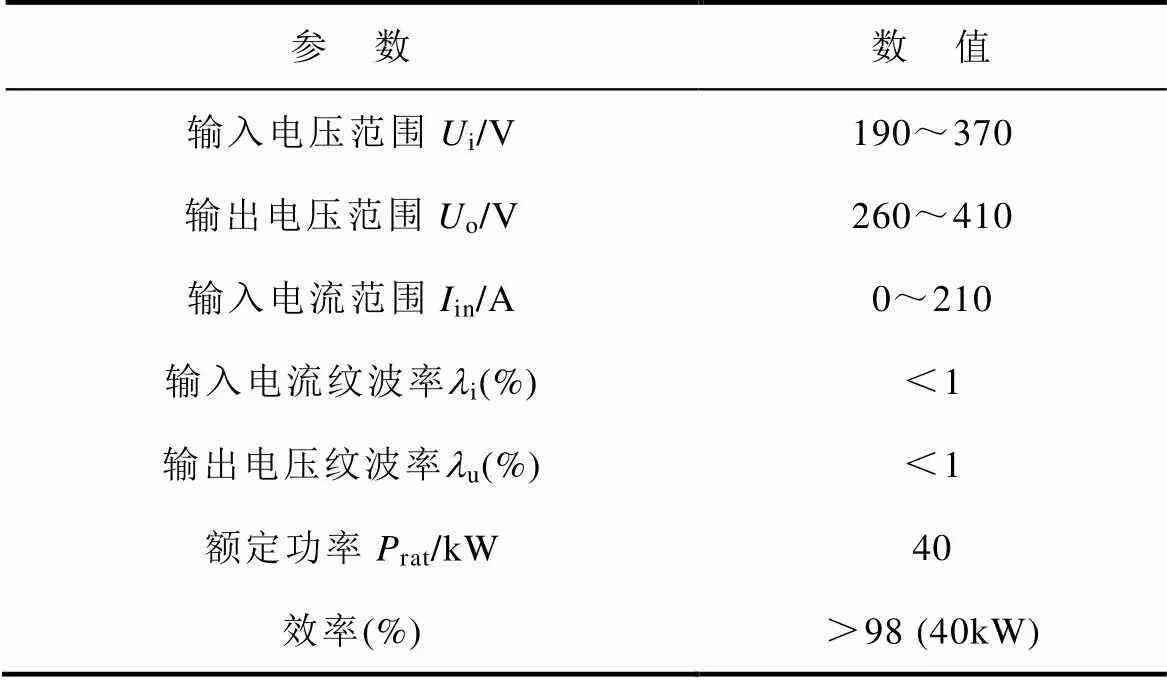
表1 变换器设计参数

2 纹波分析

纹波分析是确定开关频率和无源元件参数选型的基础。对于交错并联型变换器，其纹波要求往往指交错并联运行时的总纹波不超过限值。由图2可知，交错并联结构使得总纹波与支路纹波的关系变得复杂。因此，量化交错并联对纹波的影响是参数设计的前提。

2.1 电感电流纹波

以Boost支路1为例，电感工作于CCM，电感电流上升和下降斜率记为1、2，其计算式为

由于各支路的输入和输出均并联，总电感电流纹波Dt为1和2的组合。此外，由能量转化关系可知，当Dt上升时输出电容处于放电状态；相反，输出电容处于放电状态。Dt上升、下降斜率记为up、dn，对应时间为up和dn；总输出电流为o，每个支路输入电流为1，输入电容的充、放电电流为_up和_dn，则总电感电流纹波、输出电容电流与占空比的关系见表2。

表2 总电感电流纹波、输出电容电流与占空比的关系

对表2归纳可得，当总电感电流Dt增大时，共有个支路的主开关处于导通状态，的取值由占空比范围决定，相应地，输入电流变化率up为

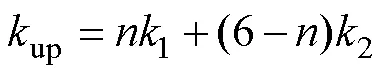
对应时间为

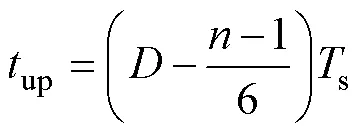
则总电感电流纹波Dt可表示为

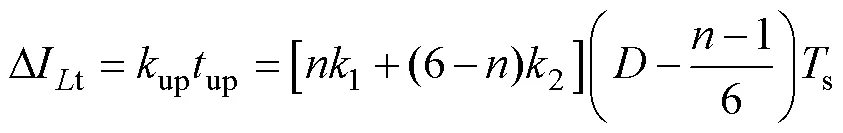
在CCM下，Boost电路的电压增益为

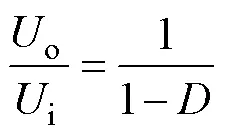
结合式（1）、式（4）、式（5）可知，总电感电流纹波DIt为

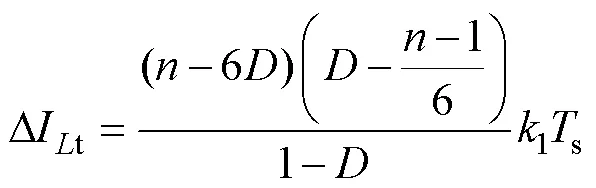
2.2 输出电压纹波

根据表2，当总电感电流上升时，输出电容放电，此时共有个支路的主开关管开通，则输出电容放电电流I_dn为

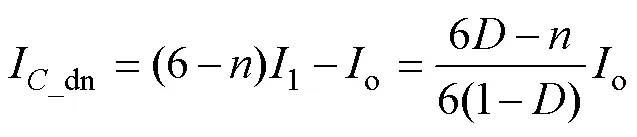
不考虑损耗情况下，1与o的关系为

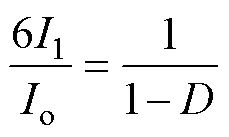
根据式（7）和表2可知，输出电压纹波Do为

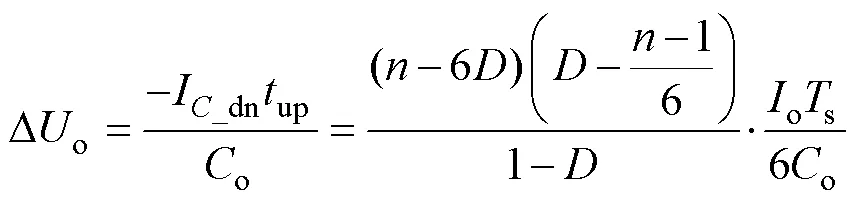
2.3 纹波抑制比

式（6）和式（9）反映了交错并联后的电流和电压纹波情况，其表达式十分复杂，这不利于变换器的参数设计，且无法直观反映出交错并联对纹波的影响。为量化这一影响，引入纹波抑制比，纹波抑制比指交错并联下的纹波与支路单独运行下的纹波之比。

当支路1单独运行时，电感电流纹波D和输出电压纹波D1分别为

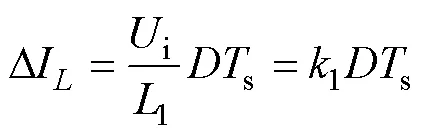
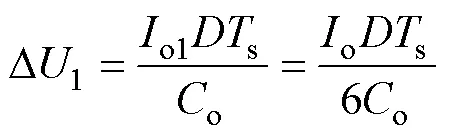
式中，o1为支路单独运行时的输出电流，其值为变换器总输出电流o的1/6。

结合式（4）、式（9）～式（11）可得，电感电流纹波抑制比K和输出电压纹波抑制比Ko为

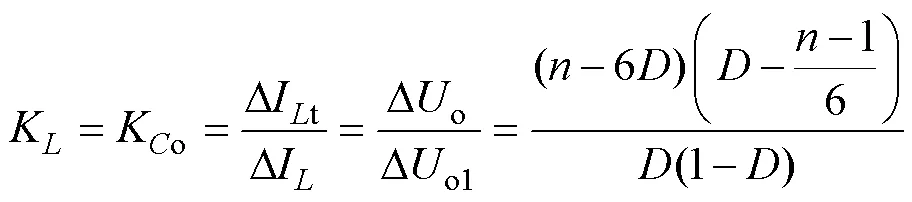
式（12）反映了纹波抑制比与占空比的关系，具体如图3所示。式（12）和图3表明，交错并联对输出电容纹波和总电感电流纹波具有相同的抑制效果；纹波抑制比随占空比呈非线性变化，在特定占空比下纹波可被完全抑制，且在不同区间上存在对称性，图3中还标注了各区间段的纹波最大值。在图3中，纹波抑制比不大于1，这说明交错并联后的纹波不超过支路单独运行时的纹波，即

图3 不同占空比下的纹波抑制比

Fig.3 Ripple suppression ratio under different duty cycle

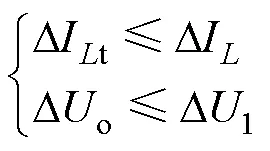
2.4 输入电压纹波

燃料电池对电流纹波非常敏感，过大的电流纹波会缩短其寿命。增大电感值可减小电流纹波，但随着电感值的增大，电感体积增大且损耗可能增加，这不利于变换器功率密度和效率的提高。因此，通常在输入侧增加电容，以吸收电感电流纹波，避免过大的电感值。

输入电容用于吸收总电感电路纹波DIt，其频率为6s，则输入电容吸收的电荷量in为

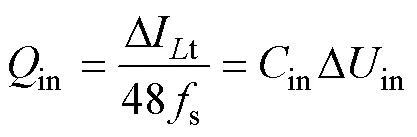
式中，Din为输入电压纹波。

结合式（14）可知，输入电压纹波Din为

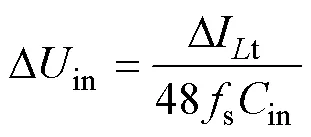
2.5 参数设计依据

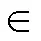
由图3和式（13）知，在交错并联变换器中最大纹波为支路单独运行时的纹波。因此，若单支路满足纹波要求，则交错并联后的纹波亦满足要求。

由式（5）、式（10）和式（11）可得，支路单独运行时，电感1与其电流纹波DI、输出电容o与电压纹波率u的关系为

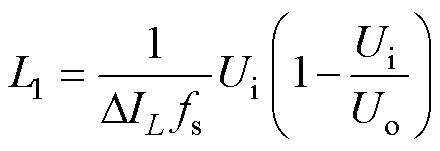
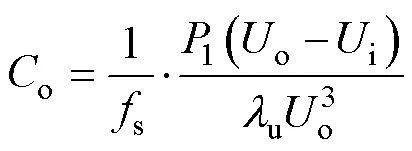
式中，1为支路功率，其值为变换器功率的1/6。

输入电压纹波Din为燃料电池内阻fu与电池内部电流纹波Dfu之积。Dfu满足了输入电流纹波要求。结合式（13）和式（15），in与电流纹波率i的关系为

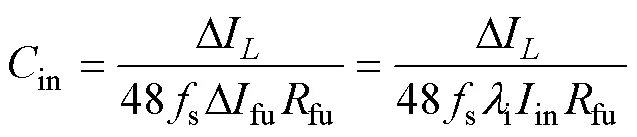
式（16）～式（18）表明，无源元件的取值与开关频率、纹波要求、功率以及输入和输出电压有关。当变换器处于纹波最大工作条件时，满足纹波要求的无源元件取值最小。结合表1和式（16）～式（18）可得，纹波最大工作条件及无源元件最小值如下。

当支路输出1=6 670W，输出电压o=285V，且i=190V时，电压纹波率u取得最大值1%。由此可得，输出电容最小值o_min为

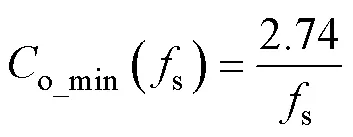
当输出电压o=410V，且输入电压i=o/2时，电感电流纹波最大，则电感最小值min为

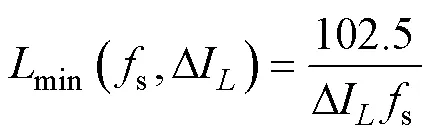
当输入电流in为最大值210A时，燃料电池电流纹波Dfu取得最大值2.1A，设燃料电池内阻fu= 200mW，则输入电压纹波Din=0.42V，可得输入电容最小值in_min为

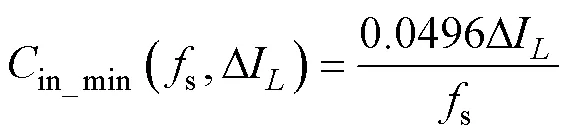
3 参数综合设计

3.1 参数综合设计流程

由式（19）～式（21）可知，无源元件的取值是关于电感电流纹波D和开关频率s的函数。D和s之间无耦合关系，在其取值范围内，对无源元件的所有结果进行效率和功率密度对比，即可获得最佳的设计参数。参数综合设计流程如图4所示，相关步骤如下。

（1）确定s和D的取值范围。文中开关频率的范围为30～200kHz，由于支路电流有效值最大为35A，则电流纹波D的取值范围为0～60.62A。

（2）s和D的步长分别设为1kHz和1A，由此可得s和D的所有组合结果。

（3）依次选取s和DI的值，代入式（19）～式（21），计算无源元件取值min、o_min和in_min。

（4）将步骤（3）的结果及s和D的取值，代入到变换器损耗模型loss和无源元件体积模型中，计算当前的损耗loss和无源元件体积和t。

（5）若损耗loss大于损耗限值loss_max，则认为s和D取值无效，重新选取s和D的值，并重复步骤（2）～步骤（4）；若损耗loss＜loss_max，则认为当前s和D的取值有效，并记录当前的体积结果t。

（6）在完成s和D的所有组合运算后，t最小值对应的s和D值即为最佳参数设计结果。

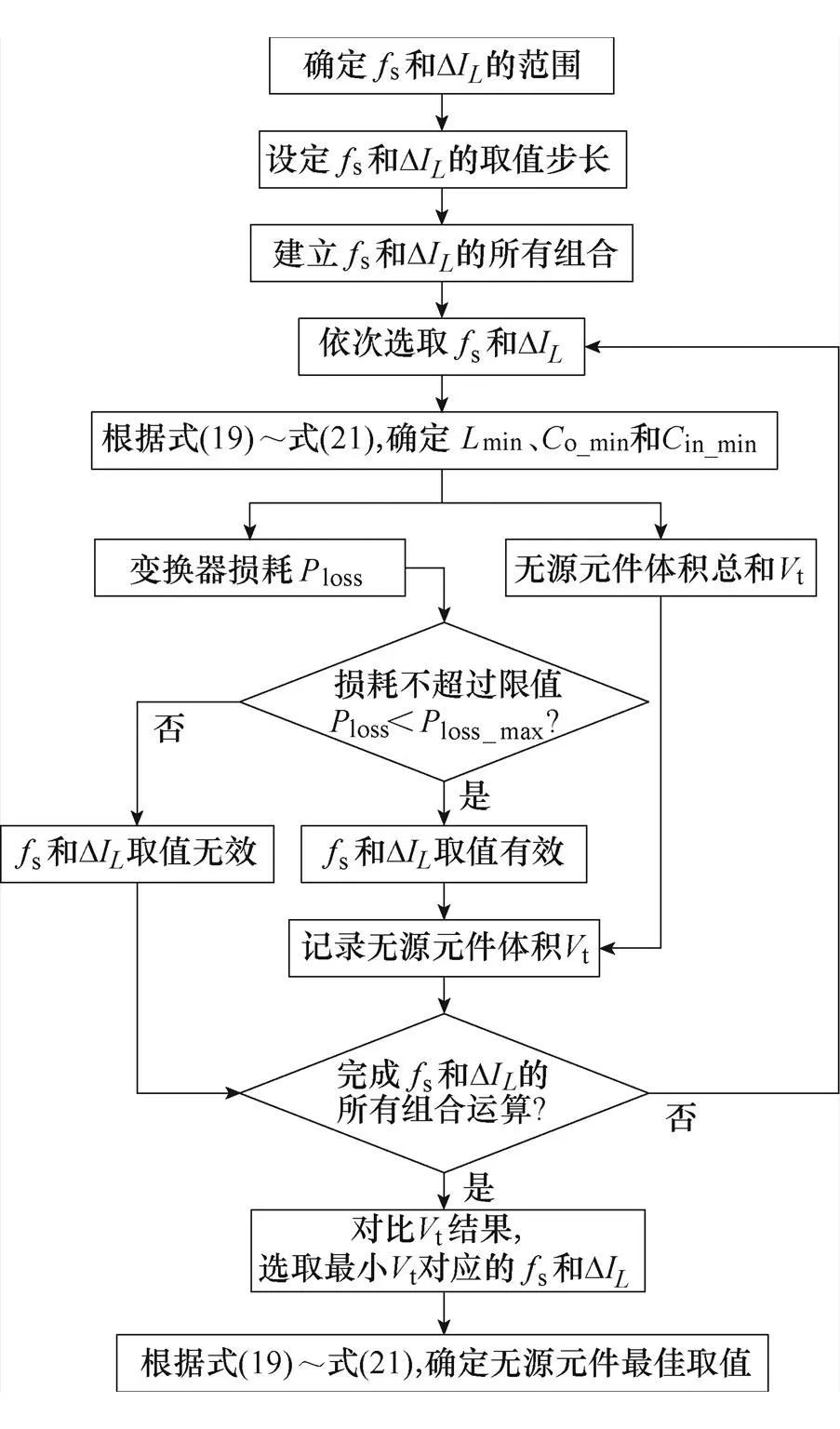
图4 参数综合设计流程

变换器损耗建模和无源元件体积建模是参数综合设计的关键。由于变换器损耗受电感体积影响，故进行损耗建模前，先需进行无源元件体积建模。

3.2 无源元件体积建模

无源元件体积建模包括电感体积建模、输入和输出电容建模。需要说明的是，电感体积不仅与数值有关，还与磁心类型、绕组匝数w和磁心截面积e有关。电容体积不仅与电容取值有关，还与电容类型有关。

3.2.1 电感体积建模

为实现大功率变换器高效率、高功率密度的设计目标，需选择具有高饱和磁通的电感磁心，且在高频下磁心损耗较小。本文所选的磁心材料为POCO NPH-L-60m，其饱和磁通为1T，100kHz下磁心损耗约为400mW/cm3（磁摆幅Dm=0.1T）。磁心结构及尺寸如图5所示，由两个方形磁心和两个圆形磁心构成，电感绕组均匀绕在圆形磁心上。

电感单匝绕组的宽为w，设磁心开窗为50%，则磁心长度m可表示为

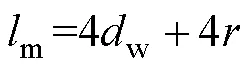
方形磁心与圆形磁心具有相同的截面积，且方形磁心宽度m与圆柱磁心直径相等，则方形磁心厚度m为

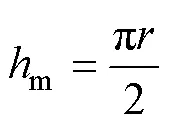
电感单匝绕组的厚为w，绕组间的距离为1，则圆形磁心的高度为

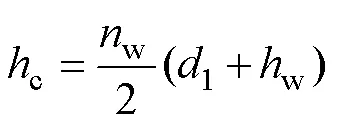
由式（22）～式（24）可知，电感体积可表示为

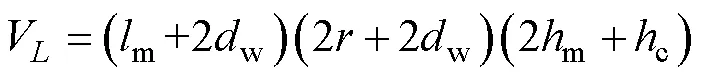
磁心体积Fe可表示为

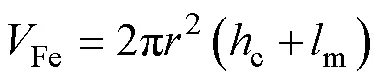
磁路e可表示为

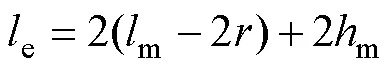
电感电流有效值最大为35A，取绕组宽w= 0.4cm，绕组厚w=0.25cm，绕组间距1=0.1cm，则和Fe可表示为关于匝数w和半径函数，即

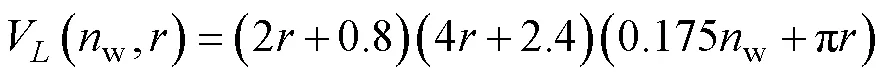
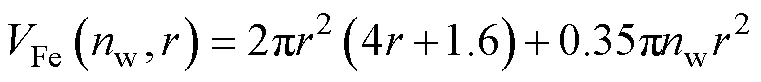
根据匝数和磁心半径可得，电感的计算式为

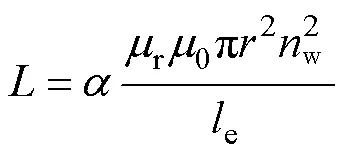
式中，r为相对磁导率，所选磁心的r=60；0为真空磁导率，0=0.4π×10-8H/m；e为等效磁路；w为绕组匝数；为磁导率衰减系数，与磁场变化频率和磁场强度有关，0.8。

结合式（30）及绕组参数可得，匝数w计算式为

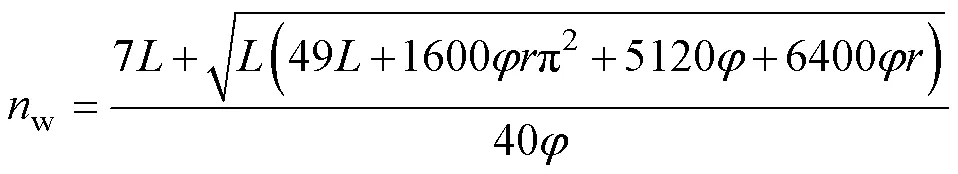
式（31）表明，对于确定的电感磁心，其体积V与和磁心半径有关。由式（20）可知，由开关频率s和电流纹波D决定。由于s、DI及三者无耦合关系，则V是关于这三个自变量的函数。在DI=10A, 20A,…, 60A时，V与s、DI及的关系如图6所示。图中，电感体积V随电流纹波DI和开关频率s的增大而减小；在确定DI和s的取值后，磁心半径过大或过小，均不利于电感体积的减小。

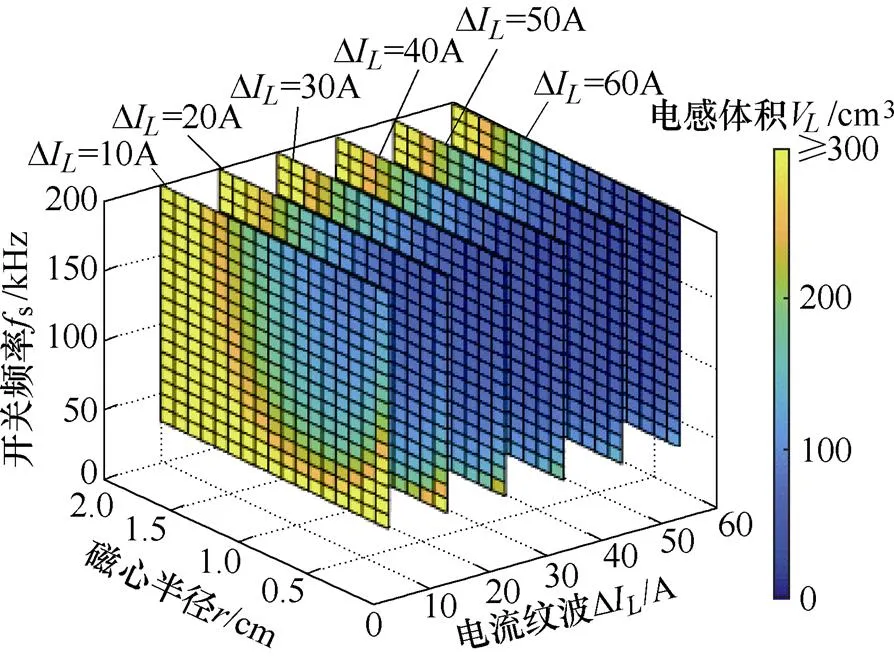
图6 电感体积VL与fs、DIL以及r的关系

同样地，磁心体积Fe也是关于s、D及的函数。在DI=10A, 20A,…, 60A情况下，磁心体积Fe与s、D及的关系如图7所示。图中，磁心体积Fe随电流纹波D和开关频率s的增大而减小，对于确定的D和s取值，磁心体积随磁心半径的减小而减小。

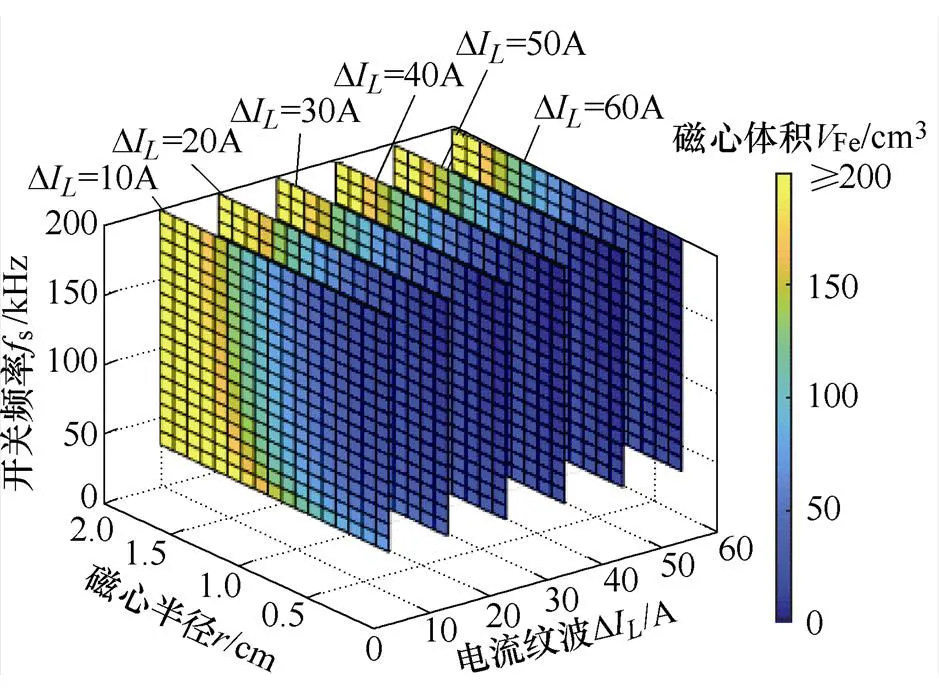
图7 磁心体积VFe与fs、DIL以及r的关系

3.2.2 电容体积建模

输入和输出电容均采用TDK薄膜电容，型号为B32776P，耐压等级为630V。该类薄膜电容（mF）与体积V（cm3）的关系如图8所示，经拟合可得两者关系为

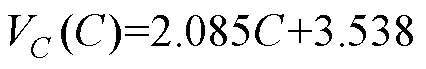
结合式（19）和式（21），可知输入电容体积Vin和输出电容体积Vo与s和D的关系为

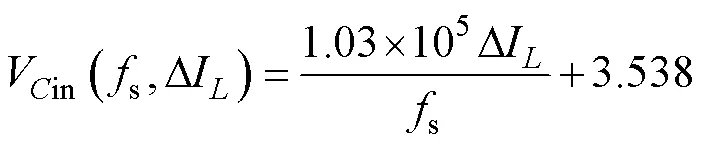
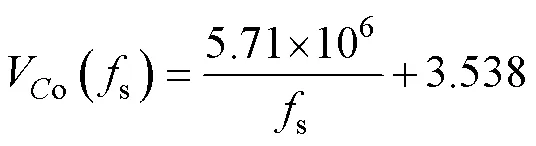
3.2.3 无源元件体积和t

结合式（28）、式（33）和式（34），无源元件体积总和t可表示为

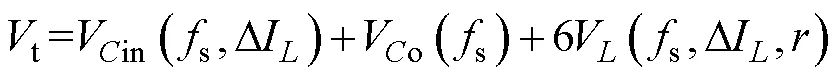
结合式（22）～式（35）可得，无源元件体积和t与s、D以及的关系如图9所示。图中，无源元件的体积和t随电流纹波D和开关频率s的增大而减小；对于确定的D和s取值，即无源元件取值确定后，t受磁心半径影响，过大或过小，t都将较大。

3.3 损耗建模

在损耗建模中，忽略输入和输出电容损耗，则变换器损耗loss包括开关管损耗H和电感损耗。每个Boost支路参数一致，若单支路满足损耗要求，变换器整体满足损耗要求，故对支路进行损耗建模。

3.3.1 半桥损耗

结合式（16）～式（18）可知，随着开关频率的提高，电容和电感的取值下降，因此提高开关频率可减小变换器体积。传统Si基功率器件在高频开关频率下，开关损耗较高。因此，在变换器设计中以SiC为开关器件。所选SiC型号为英飞凌IMZ120R045M1，主要参数见表3。

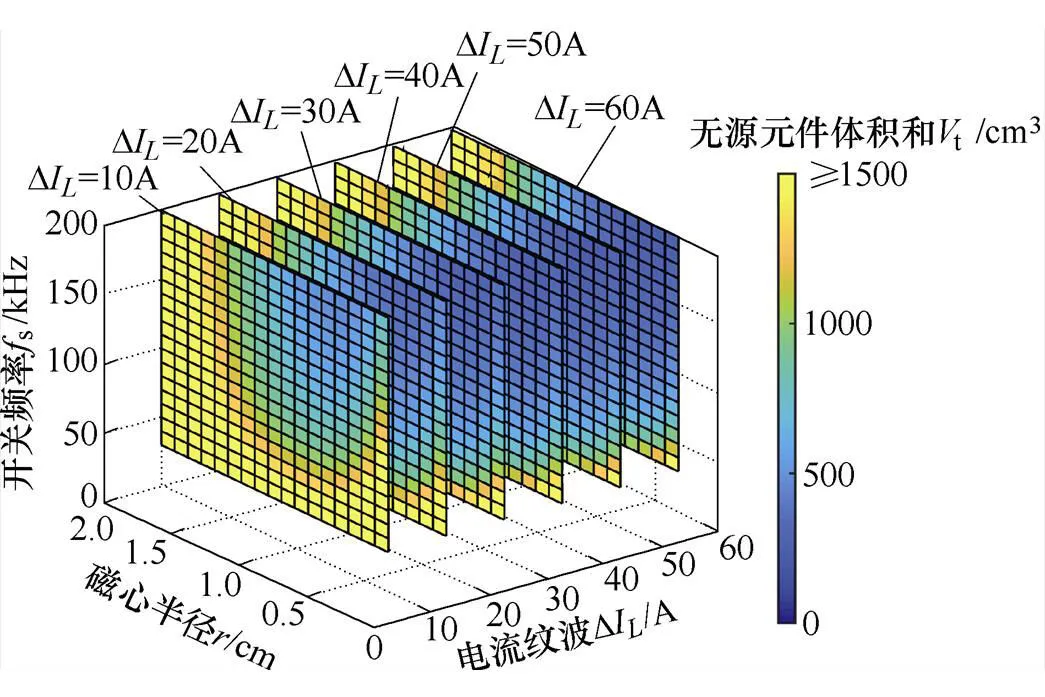
图9 无源元件体积和Vt与fs、DIL以及r的关系

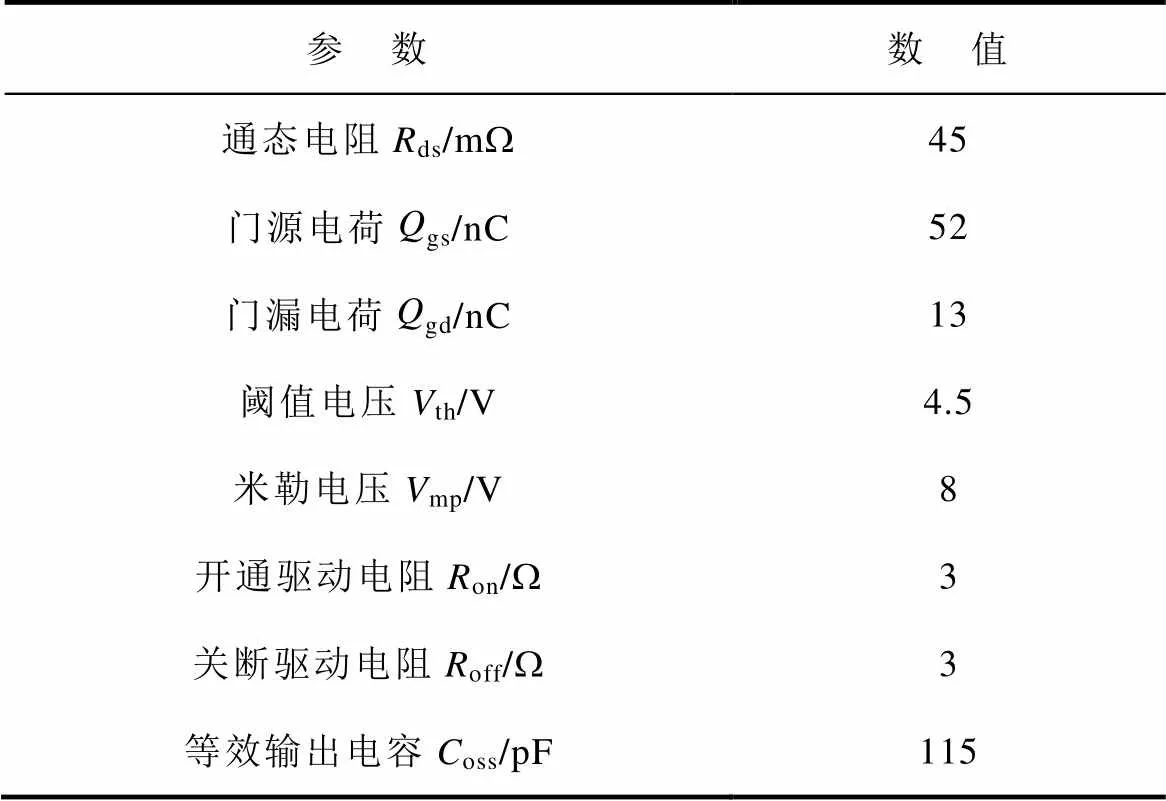
表3 英飞凌IMZ120R045M1主要参数

对于同步整流管而言，开通和关断均在零电压软开关（Zero Voltage Switching, ZVS）条件下进行，故其损耗只考虑导通损耗con1。主开关管工作于硬开关状态，其损耗包括开通损耗on、关断损耗off、导通损耗con2和输出电容损耗oss。同步整流管和主开关管的导通损耗con为

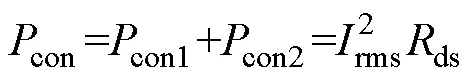
输出电容损耗oss为

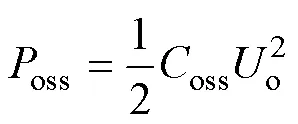
max和min为电感电流最大值和最小值，两者与电流纹波D和有效值rms的关系为

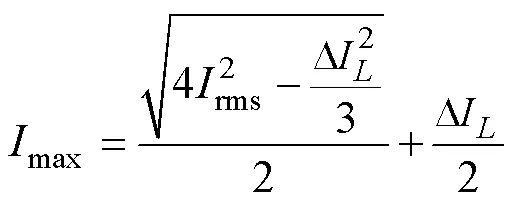
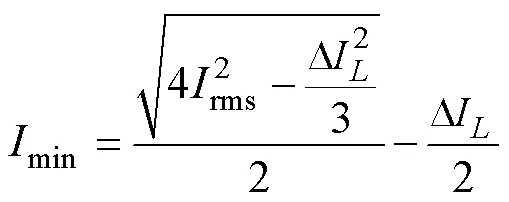
由此可得，主开关管开通和关断损耗为

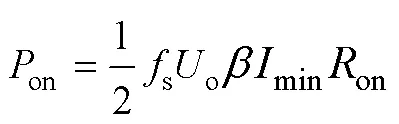
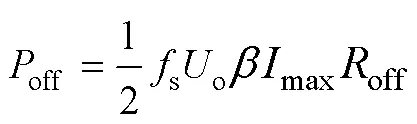
其中

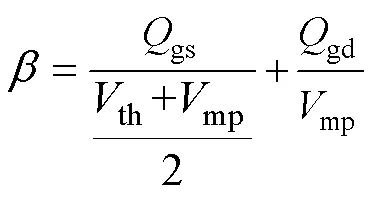
结合式（36）～式（41）及表1可知，当o=410V，支路电流有效值rms取最大值35A时，H最大，即

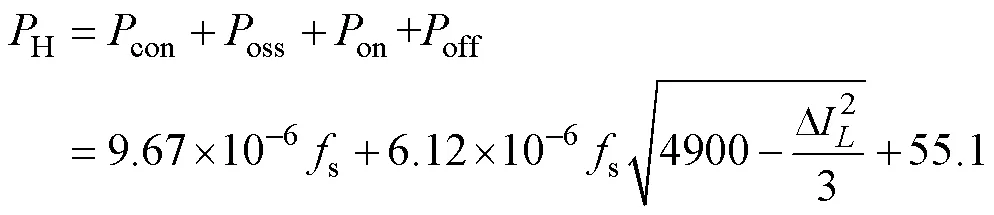
3.3.2 电感损耗建模

电感损耗包括铜损Cu和铁损Fe（MW）。计算铜损Cu前，首先需要计算绕组内阻Cu。

绕组长度Cu可表示为

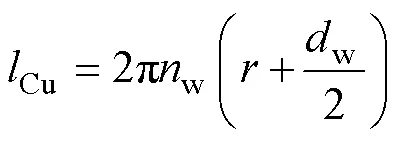
电感绕组材料为铜，其内阻Cu可表示为

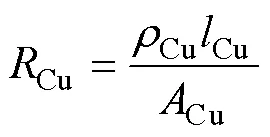
式中，Cu为绕组截面积，Cu=10mm2；Cu为铜的电阻率，Cu=1.78×10-8W/m。

结合绕组参数，铜损Cu可表示为

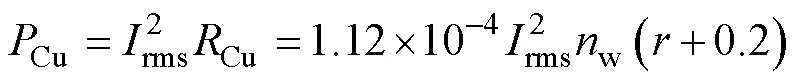
电流有效值rms取最大值35A时，铜损最大。结合式（31），铜损可进一步表示为

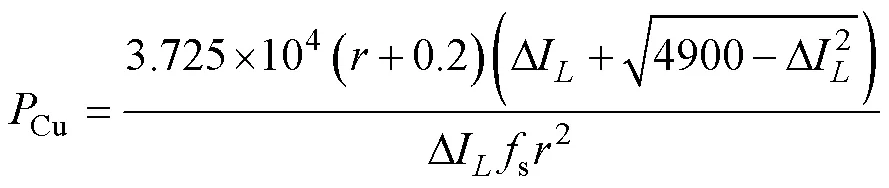
由所选磁心的手册可知，电感铁损Fe的计算式为

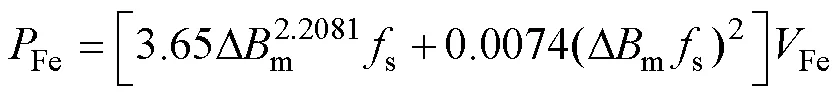
式中，Fe为磁心体积（cm3）；Dm为最大磁摆幅（kGs）；s的单位为kHz。

磁摆幅Dm与电流纹波D的关系为

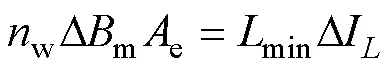
由式（31）和式（48）可知，磁心损耗Fe是关于s、D以及的函数，在损耗计算过程中需注意单位换算。

3.3.3 变换器损耗

变换器损耗loss是关于s、DI以及的函数。在特定电感电流纹波下，损耗结果如图10所示。由图可知，变换器损耗与s、DI呈正相关，即s、DI越大，loss越大。此外，磁心半径过大或过小均会导致损耗增大。

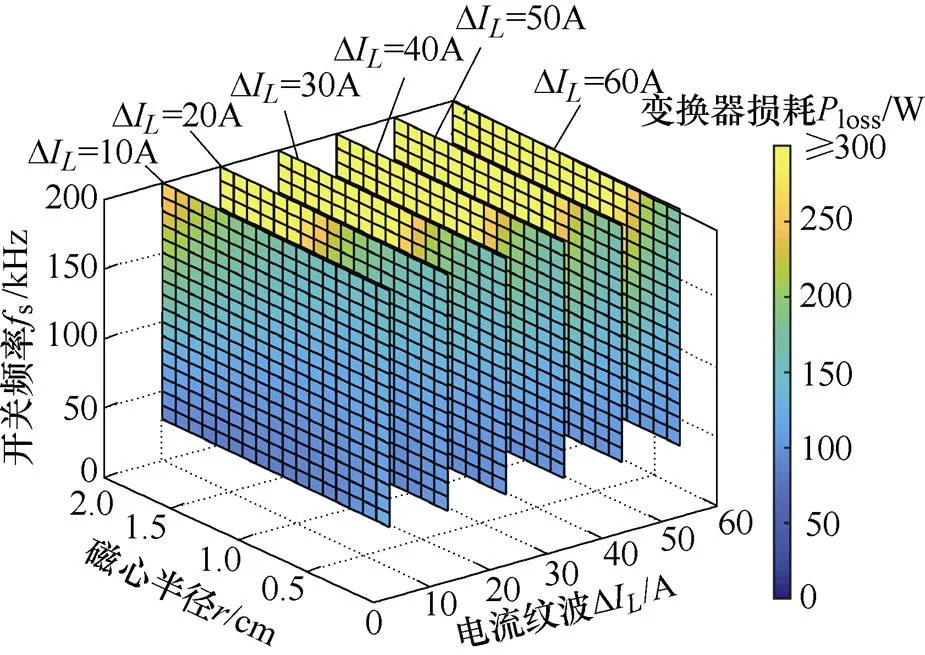
图10 变换器损耗Ploss与fs、DIL以及r的关系

图9和图10反映了变换器损耗和功率密度间的矛盾关系：增大s和D均可减小无源元件体积，但导致了损耗的增加。此外，过大或过小的均不利于减小损耗和提高功率密度，这也反映了合理的磁心尺寸对变换器优化设计的重要性。

3.4 参数设计结果

变换器的参数设计原则是，满足损耗限制的情况下，尽可能提高功率密度。结合表1，为使效率高于98%，则单支路的最大损耗不超过133W。考虑实际工况的复杂性，在参数设计中最大损耗设定为110W。为使纹波满足要求，设计过程中无源元件参数考虑50%的设计余量，则电压和电流纹波率均取为0.67%。

由式（42）、式（46）和式（47）可得，损耗小于110W的参数设计结果如图11所示。由图可知，为满足损耗要求，开关频率s须小于120kHz，磁心半径须大于0.5cm；电流纹波越大，s和的选择范围越小。

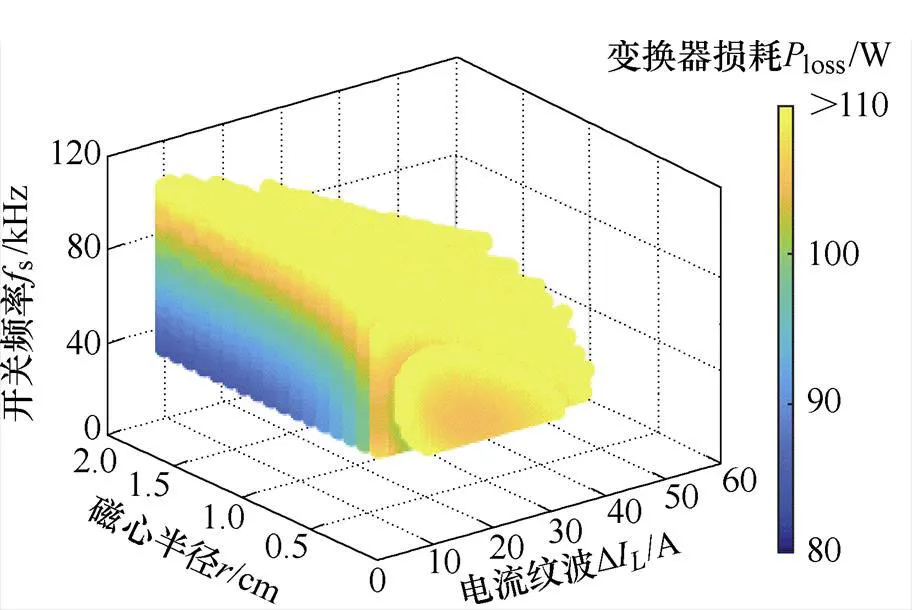
图11 Ploss＜110W对应的fs、DIL及r取值

将图11中s、DI及取值结果代入无源元件体积模型，可得满足损耗要求的无源元件体积之和t，其中t＜800cm3的取值结果如图12所示。在所有的t结果中，最小体积为692cm3，相应的参数为s=80kHz，0.6cm，DI=23A。

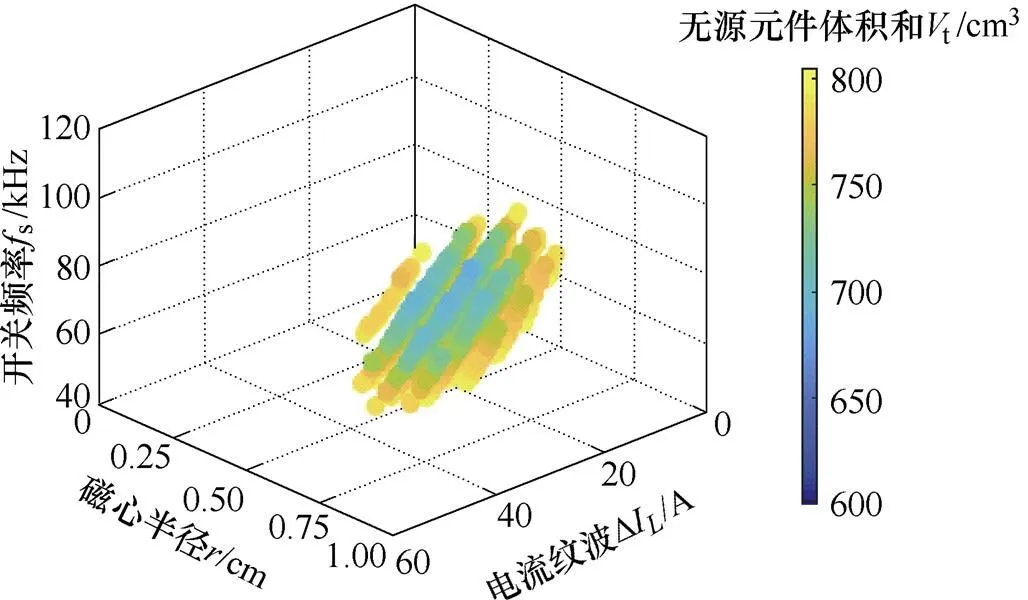
图12 Ploss＜110W且Vt＜800cm3对应的fs、DIL及r取值

将上述参数设计结果代入式（16）～式（18）中，输入和输出电容取值为21.39mF和51.38mF，电感值为55.7mH。结合式（31）得，绕组匝数w=42.8。w取正偶数结果即44匝，代入式（30）后，电感最终值取为57.71mH。

4 仿真及实验验证

结合变换器设计要求和参数设计结果，首先搭建仿真平台证明理论分析的正确性和所述方法的可行性。仿真过程中，开关频率为80kHz，输入电压为i=200V。结合图3知，占空比取0.4时纹波抑制比较大，便于进行纹波对比。支路仿真功率为6.67kW，在单支路和6支路交错运行下进行仿真。

6路交错并联运行下的电流仿真结果如图13所示。由图可知，支路电感电流纹波为17.6A，总电感电流纹波t=3.05A，两者之比为0.173，与式（12）计算结果接近。此外，总电感电流It和输入电流in的对比验证了输入电容吸收电流纹波的有效性。

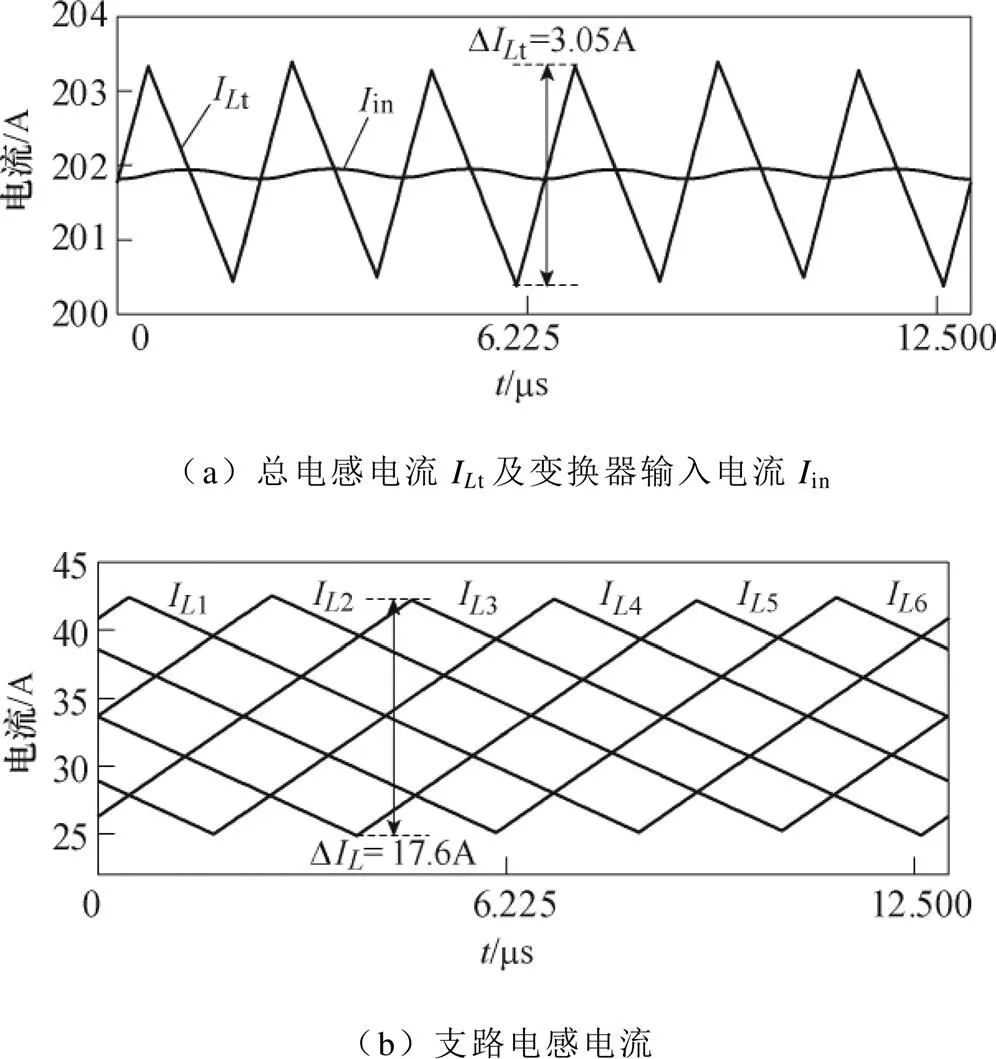
图13 电流纹波仿真结果

支路单独运行和6路交错并联运行时的电压纹波对比如图14所示。图中，支路单独运行时的电压纹波为1.65V，6路交错并联下的电压纹波为0.29V，两者之比约为0.176，同样与式（12）计算结果接近。图13和图14表明交错并联结构对电压和电流纹波具有相同的抑制效果，且验证了纹波分析的正确性。

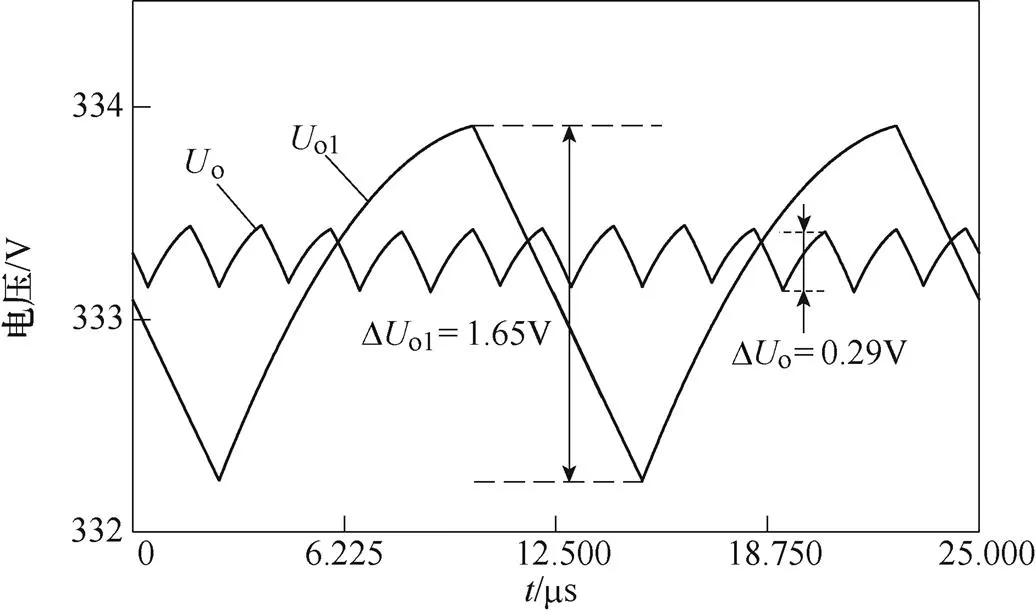
图14 输出电压纹波仿真结果

基于参数设计结果，搭建实验样机如图15所示。样机以TMS320F28379D为控制核心，开关频率取值以及无源功率器件的设计与图12设计结果一致，即开关频率为80kHz，电感磁心半径为0.6cm，绕组匝数为44匝，输入和输出电容均为TDK 630V，30mF的薄膜电容型号为B32776P6306K，基于图12和式（16）～式（18），输入和输出电容的取值分别为21.39mF和51.38mF，因此输入和输出侧电容的数量分别为1个和2个。变换器尺寸为35cm×29cm× 10cm，相应的功率密度为66W/in3（1in3=1.638 71× 10-5m3）。

图15 交错并联变换器实验样机

在输入电压为205V且占空比为0.5时，进行额定功率实验。图16为变换器主开关管驱动信号波形。图中，变换器开关频率为80kHz，相邻驱动信号的时间间隔为2.1ms，对应相位差为60°，这与变换器6路交错并联工作方式相一致。

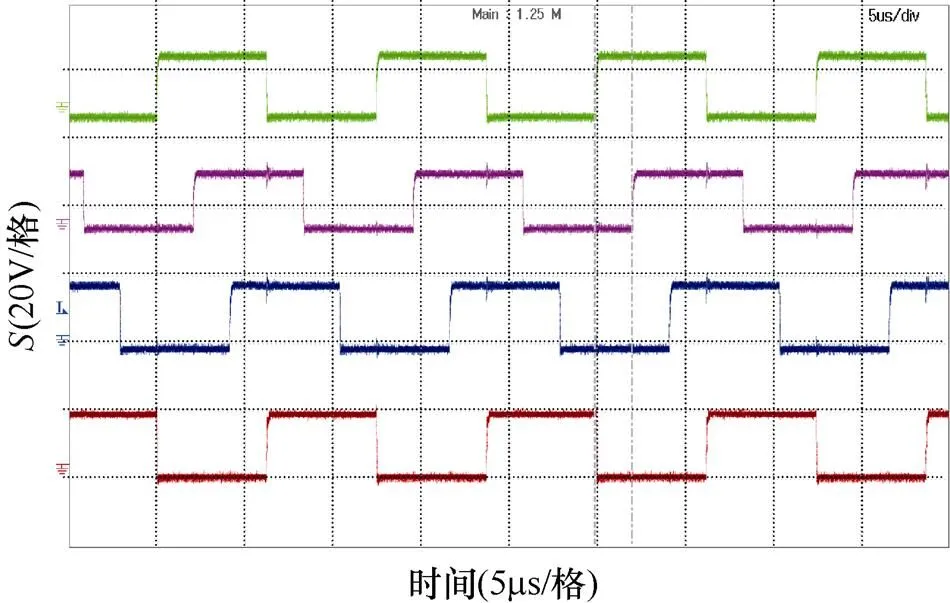
图16 6路交错运行中的驱动信号波形

额定功率下的电感电流及输出电压波形如图17所示。图中，支路1和2的电感电流纹波频率及相位差与图16中的驱动信号相对应；经测量，电流纹波幅值为18A，小于前文的纹波限值23A，输出电压纹波为2V，小于输出电压纹波要求。图17表明，额定功率下变换器处于正常工作状态且满足纹波设计要求。

通过功率分析仪，进一步验证变换器的效率特性。由于各支路参数一致，则单支路效率可反映变换器的整体情况。在输入电压为205V，输出电压为410V时，单支路运行情况下的效率曲线如图18所示。图中，额定功率6.67kW下，单支路效率为98.08%，且变换器在较宽的功率范围内效率均高于98%。图18表明，根据所提参数设计方法，变换器具有较好的效率特性。

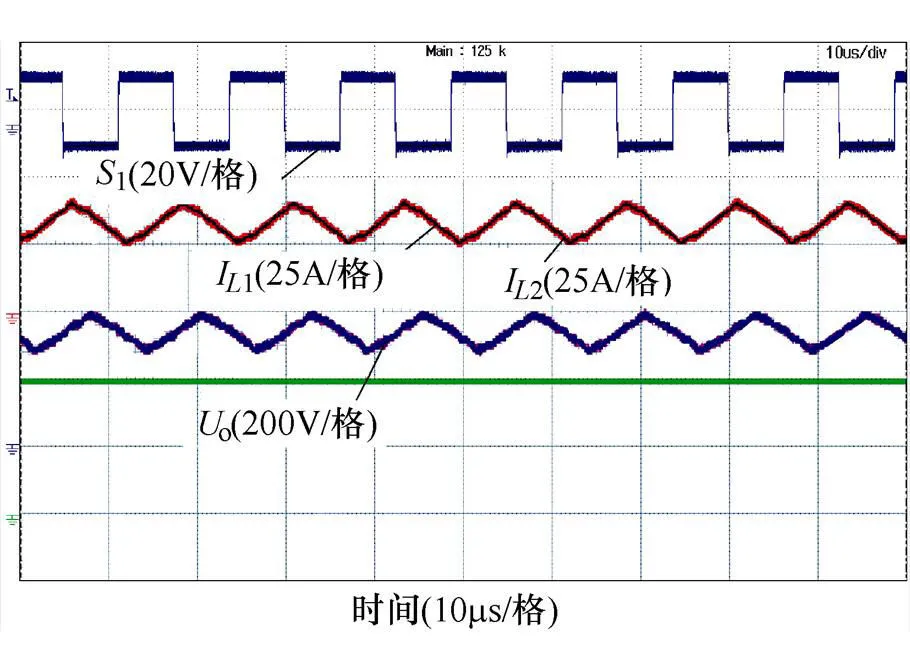
图17 额定功率下驱动信号、输出电压和电感电流波形

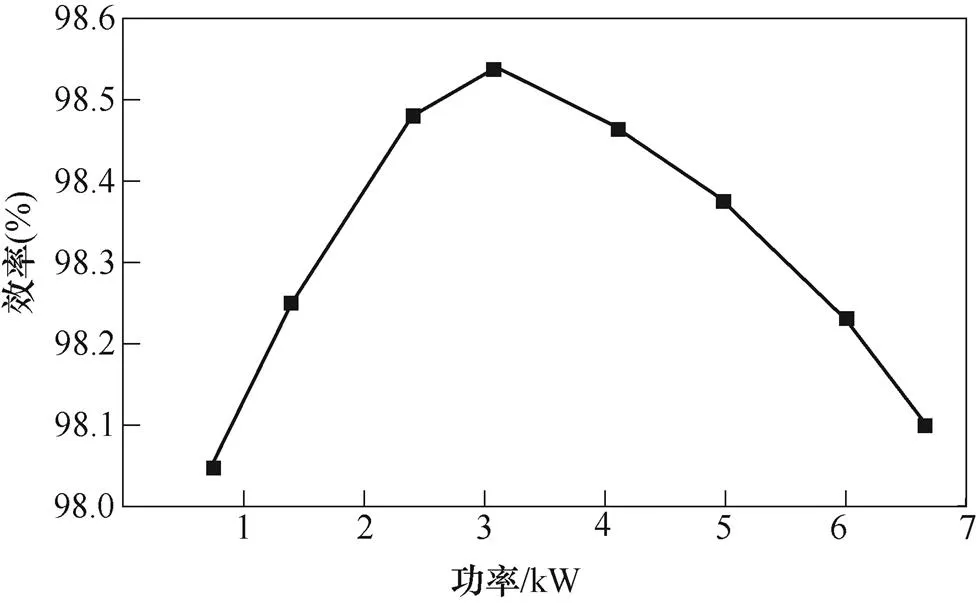
图18 单支路效率曲线

5 结论

以燃料电池用交错并联型Boost变换器为研究对象，本文提出了一种兼顾效率与功率密度的参数综合设计方法，并通过搭建40kW实验样机，验证了理论分析的正确性和所提方法的可行性。所得结论如下：

1）交错并联使得纹波分析复杂化，本文引入纹波抑制比量化分析了变换器单支路运行与多支路交错运行下的纹波关系，该关系为交错并联变换器的参数设计依据。

2）以开关频率s、电感电流纹波DI及电感磁心半径为自变量，实现对变换器效率和无源元件体积的统一建模，从而为兼顾效率和功率密度的综合优化设计提供了前提。

3）所提方法可应用于其他交错并联型变换器的参数设计与综合优化中。

[1] 罗悦齐, 张嵩, 高丽萍, 等. 质子交换膜燃料电池低温启动水热管理特性及优化[J]. 电工技术学报, 2018, 33(11): 2626-2635.

Luo Yueqi, Zhang Song, Gao Liping, et al. Optimi- zation of water and thermal management in proton exchange membrane fuel cell during low temperature startup[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2626-2635.

[2] Gao Shanshan, Wang Yijie, Guan Yueshi, et al. A high step up Sepic-based converter based on partly interleaved transformer[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1455-1465.

[3] Wang Yijie, Qiu Yuping, Bian Qing, et al. A single switch quadratic Boost high step up DC-DC con- verter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4387-4397.

[4] 戚志东, 裴进, 胡迪. 基于分数阶PID控制的质子交换膜燃料电池前级功率变换器[J]. 电工技术学报, 2019, 34(21): 235-243.

Qi Zhidong, Pei Jin, Hu Di. Pre-stage power converter of proton exchange membrane fuel cell based on fractional order PID controller[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 235-243.

[5] Banaei M R, Sani S G. Analysis and implementation of a new Sepic-based single-switch Buck-Boost DC-DC converter with continuous input current[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10317-10325.

[6] Nonobe Y. Development of the fuel cell vehicle Mirai[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2017, 12(1): 5-9.

[7] Lai J, Ellis M W. Fuel cell power systems and applications[J]. Proceedings of the IEEE, 2017, 105(11): 2166-2190.

[8] 胡雪峰, 戴国瑞, 龚春英, 等. 一种高增益低开关应力改进交错型Boost变换器[J]. 电工技术学报, 2014, 29(12): 80-87.

Hu Xuefeng, Dai Guorui, Gong Chunying, et al. An improved interleaved Boost converter with high gain and low switch voltage stress[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 80-87.

[9] Rana N, Banerjee S. Development of an improved input-parallel output-series Buck-Boost converter and its closed-loop control[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6428-6438.

[10] 曹勇, 杨飞, 李春晖, 等. 不同耦合系数下的交错并联电流连续模式Boost功率因数校正变换器的传导电磁干扰[J]. 电工技术学报, 2019, 34(10): 2176- 2186.

Cao Yong, Yang Fei, Li Chunhui, et al. Conducted electromagnetic interference of interleaved con- tinuous current mode Boost power factor correction converter with different coupling coefficients[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2176-2186.

[11] Yang Yugang, Guan Tingting, Zhang Shuqi, et al. More symmetric four-phase inverse coupled inductor for low current ripples & high-efficiency interleaved bidirectional Buck/Boost converter[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(3): 1952- 1966.

[12] Forest F, Meynard T A, Huselstein J, et al. Design and characterization of an eight-phase-137-kW intercell transformer dedicated to multicell DC-DC stages in a modular UPS[J]. IEEE Transactions on Power Elec- tronics, 2014, 29(1): 45-55.

[13] Hartnett K J, Hayes J G, Egan M G, et al. CCTT-core split-winding integrated magnetic for high-power DC-DC converters[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4970-4984.

[14] Hegazy O, Mierlo J V, Lataire P. Analysis, modeling, and implementation of a multidevice interleaved DC/DC converter for fuel cell hybrid electric vehicles[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4445-4458.

[15] Priya M S, Balasubramanian R. Analysis of multide- vice interleaved Boost converter for high power applications[C]//2014 International Conference on Circuits, Power and Computing Technologies, Nagercoil, India, 2014: 320-327.

[16] Nussbaumer T, Raggl K, Kolar J W. Design guidelines for interleaved single-phase Boost PFC circuits[J]. IEEE Transactions on Industrial Elec- tronics, 2009, 56(7): 2559-2573.

[17] Raggl K, Nussbaumer T, Doerig G, et al. Com- prehensive design and optimization of a high- power- density single-phase Boost PFC[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2574-2587.

[18] Xu Hengshan, Chen Diyi, Xue Fei, et al. Optimal design method of interleaved Boost PFC for improving efficiency from switching frequency, Boost inductor, and output voltage[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6088-6107.

Comprehensive Parameter Design Method of Interleaved Boost Converter for Fuel Cell Applications

1112

（1. Key Laboratory of Smart Grid of Ministry of Education Tianjin University Tianjin 300072 China 2. State Grid Tianjin Economic Research Institute Tianjin 300171 China）

Taking the interleaved boost converter for fuel cell as the research target, a comprehensive parameter design method is proposed considering efficiency and power density. Firstly, the voltage and current ripple are compared in single-branch and multi-branch interleaved operation. Ripple suppression ratio is introduced to quantify the effect of interleaved structure, thereby establishing the relationship between the ripple requirement and parameters of the single branch, and consequently the parameter design is carried out. During the process of comprehensive design, the switching frequencys, the inductor current rippleDIand the radius of inductor coreare chosen as independent variables to establish the power loss and passive device volume model. Power loss less than the set value is set as the constraint condition, the minimum volume of passive components is the design object, the optimal independent variables are chosen. Then, the optimal value of the capacitor and the design of the inductor are carried out, and the comprehensive design considering efficiency and power density is achieved. Finally, the correctness of theoretical analysis and the feasibility of the parameter design method are verified via the simulation and a 40kW prototype.

Fuel cell, interleaved, Boost converter, parameter design and optimization

TM46

10.19595/j.cnki.1000-6753.tces.L90309

2020-07-09

2021-01-02

马小勇 男，1991年生，博士研究生，研究方向为高频大功率电能变换技术。

E-mail: maxiaoyong1991@126.com

王议锋 男，1981年生，博士，副教授，研究方向为高频电能变换技术、磁集成技术、软开关技术及交直流微电网中的电力电子技术等。

E-mail: wayif@tju.edu.cn（通信作者）

（编辑 陈 诚）