透水砖堵塞程度对径流颗粒物冲刷规律的影响
杜晓丽,郑泽东,尹子杰,杨明哲
(1.北京建筑大学环境与能源工程学院城市雨水系统与水环境教育部重点实验室,北京 100044;2.北京建筑大学未来城市设计高精尖创新中心,北京 100044)
透水铺装是一种常用的径流原位入渗设施,其铺设之初在雨水径流体积削减、径流污染控制等方面发挥显著效能[1-3]。许多学者对此开展了研究,如赵远玲等[4]以构造透水砖和普通透水砖为研究对象,在分别模拟不同重现期降雨时发现2种透水砖的场次降雨总量控制率均可达到95%以上;黄国如等[5]选取了20场实际降雨径流分析透水铺装对径流量的削减效果,发现透水铺装对径流体积削减率最高可达86.5%;Zhang等[6]发现透水铺装对径流COD、TN及NO3-N具有显著净化效果。但是,透水铺装系统在实际应用中面临严重堵塞问题[7]。地表径流携带的泥沙颗粒、有机物碎屑、油污等路面沉积物会进入透水铺装骨料孔隙,使其渗透性能降低、使用寿命缩短,最终演化成为不透水路面[8-9]。Al-Rubaei等[10]对瑞典北部两种不同材质透水沥青长期监测发现,运行18年和24年后,透水沥青渗透系数衰减率均达到90%以上;王兴桦等[11]对西安市多条铺设透水砖道路进行实地调研,发现使用2年后的透水砖渗透性能衰减率为20%~68%。可见,堵塞后的透水铺装系统渗透速率大大降低,对径流体积的削减效果也大打折扣,这必然伴随着对径流污染控制效能降低,使径流污染物输出量增加。
目前,关于透水铺装系统对雨水径流污染控制的研究多集中于其铺设初期对径流中各种污染物的控制效果[12-13],却鲜有关于其堵塞失效演变而导致径流污染物输出规律变化的相关报道。如Drake等[14]研究了加拿大安大略省某新建停车场内透水沥青对径流水质控制效果,发现其明显削减了TSS、石油烃及颗粒态重金属浓度;Niu等[15]通过搭建实验室透水砖系统模拟装置,发现其对径流中SS去除率可达到79.8%以上。鉴于径流中多种污染物均附着于颗粒物上同步输出[16-17],因此本文以典型透水铺装系统——透水砖系统为研究对象,开展透水砖堵塞失效全过程对径流颗粒物冲刷规律影响的研究,并基于传统指数冲刷模型建立与透水砖堵塞程度相适应的径流颗粒物冲刷模型,描述透水砖堵塞动态变化过程对径流颗粒物控制效能的变化趋势,以期为研究透水砖堵塞全过程演化对径流中其他污染物的控制衰减规律影响提供理论支撑,这对衡量评价透水砖在城市排水系统中的作用机制、合理判定其运行维护周期等均具有重要理论意义和实用价值。
1 材料与方法
1.1 试验装置
1.1.1模拟人行道透水砖系统
模拟人行道透水砖系统为100 cm×50 cm×80 cm(长×宽×高)的无盖箱体装置,具体构造如图1所示。装置内部由下至上依次装填土基层20 cm、砾石基层20 cm和找平层4 cm,其中土基层采用素土夯实(夯实度大于90%)、砾石基层采用级配砾石、找平层和填充砖缝采用级配砂,面层选用普通混凝土透水砖(购于北京爱道爱和科技有限公司),尺寸为200 mm×100 mm×60 mm,此类型透水砖因其优良渗透、抗压性能在步行道、停车场、公园等广泛应用[4]。铺设所用素土、砾石与砂级配,以及各构造层压实度等要求参照CJJ/T 188—2012《透水砖路面技术规程》。在装置面层沿长边设置宽2 cm、坡度1%的水泥抹面沟槽,沟槽底距透水砖表面5 cm,于沟槽最低处设置取样口1用于采集透水砖表面径流;土基层和砾石基层交界处设置取样口2,用于采集透水砖系统下渗出流。

(a) 正视图

(b) 俯视图图1 模拟人行道透水砖系统Fig.1 Simulated permeable brick system of sidewalk
1.1.2模拟降雨装置
自制100 cm×100 cm管道喷淋装置进行模拟降雨,具体构造如图2所示。喷淋装置采用44根DN15 PVC管以平行并排方式连接,单根管每隔2 cm

(a) 正视图
打孔安装针头布水器;根据所需降雨重现期使用水泵出水管端流量计调整模拟降雨量。为确定降雨均匀程度以及实际降雨量和目标降雨量之间的相对误差,在模拟降雨装置下方均匀布置16个1 L量筒,利用调试好的模拟降雨装置依次模拟北京市重现期为3年一遇和10年一遇均匀降雨25 min,随后读取16个量筒中体积并换算为降雨强度,采用Christiansen均匀系数法评价降雨均匀程度,计算方法见式(1),根据式(2)计算实际降雨量和目标降雨量之间相对误差[18],结果显示3年一遇、10年一遇情况下Christiansen均匀系数分别为89.61%、85.62%,相对误差分别为1.25%、2.87%,符合均匀降雨及目标降雨重现期要求。
(1)
式中:CUC为Christiansen均匀系数,%;Di为i号量筒中的降水量,cm;Davg为量筒中的平均降水量,cm;n为量筒数量。
(2)
式中:I为降雨强度,mm/h;t为降雨持续时间,min。
1.2 试验设计
根据北京市多年降雨数据确定雨季平均干期时长为72 h,采用人工清扫和吸尘器清扫(干式吸尘器)并用方式,对北京市大兴区某人行道透水砖干期颗粒沉积物累积质量进行调研监测,获知0.5 m2透水砖表面72 h干期沉积物累积质量约为10 g。为保证还原透水砖表面颗粒物实际累积状况,每次降雨前在透水砖装置表面使用多孔筛均匀布撒10 g采集的透水砖路面颗粒沉积物。随后,分别模拟北京市重现期为3年一遇(I=49.7 mm/h)和10年一遇(I=64.8 mm/h)均匀降雨,以透水砖表面产流时记为0时刻,使用HOBO RG3-M型翻斗式雨量计(Onset,美国)实时记录取样口1出流量,并使用棕色玻璃瓶收集第5、10、15、20、25 min径流水样。场次降雨结束后,读取雨量计示数,得到径流过程逐分钟径流量数据。测定采集径流中的悬浮物(SS)质量浓度,并使用Mastersizer 3 000粒度分布仪(Malvern Panalytical,美国)测定其中的颗粒物粒径分布。
1.3 透水砖堵塞程度判定
每次降雨结束后关闭取样口1阀门,打开取样口2阀门,保持透水砖上方2 cm恒水头使用量筒采集取样口2入渗出流量,直至取样口2出水流量达到稳定后,采用达西定律(式3)计算渗透系数[19],并采用式(4)计算此时透水砖堵塞程度。待透水砖表面干燥、装置内蓄滞雨水排空后,重复上述降雨过程直至透水砖完全堵塞(堵塞程度为90%时即认为透水砖系统完全堵塞)。
(3)
式中:Q为透水砖的稳定出流量,m3/s;K为渗透系数,m/s;H为常水头高度,m;L为水流的路径,m;A为过水断面面积,m2;J为水力坡度。
(4)
式中:r为透水砖堵塞程度,%;Kinitial为透水砖初始未堵塞时渗透系数,mm/min;Ki为每次降雨结束后透水砖渗透系数,mm/min。
1.4 指数冲刷模型
采用Sartor等[20]于1974年提出的指数冲刷模型定量分析透水砖在不同堵塞程度时的初期冲刷效应,计算公式为
W=M0(1-e-kt)
(5)
式中:W为t时刻被冲刷污染物累积质量,g;M0为降雨开始时颗粒物累积量,g;k为冲刷模型系数,与颗粒物粒径、径流量有关,min-1。
2 结果与分析
2.1 透水砖堵塞程度对径流颗粒物冲刷影响
2.1.1不同堵塞程度透水砖径流中颗粒物初期冲刷效应
当雨水径流污染物初期累积排放速率大于径流累积输送速率时,即认为存在初期冲刷效应。采用无量纲M(V)曲线法(曲线全部位于45°度对角线以上认为存在初期冲刷现象)、F30参数法(F30是指场次降雨累积径流比为30%时,对应的累积污染物负荷比与累积径流比之比,F30值大于1.67时认为存在初期冲刷现象)分别对不同堵塞程度的透水砖径流颗粒物初期冲刷效应进行定性、定量判定[21-22]。一般而言,M(V)曲线距对角线离散程度越大、F30值越大时,初期冲刷效应越强烈。
选取透水砖堵塞程度r为20%、50%、70%及90%,降雨重现期3年一遇和10年一遇时场次降雨径流过程,绘制径流冲刷颗粒物M(V)曲线,并计算F30值,结果分别如图3和表1所示。由图3可见,不同降雨重现期条件下,各堵塞程度透水砖的径流颗粒物M(V)曲线均位于45°度对角线以上,且F30值均在1.67以上,说明无论透水砖堵塞与否,其表面径流颗粒物均存在初期冲刷效应。但在相同堵塞程度下,10年一遇降雨条件下F30值均高于3年一遇降雨,说明降雨重现期越大其表面径流颗粒物初期冲刷效应越明显;这是由于降雨强度较大对地表颗粒物的冲击力度较高,易打破干期累积时颗粒物与下垫面表层的平衡稳定附着状态,且径流量增大为颗粒物冲刷提供了水动力条件,导致其迁移输送率更高[22-25]。由表1可见,在同一降雨重现期下,透水砖堵塞进程后期径流的F30值大于堵塞中期和前期,说明透水砖堵塞程度越高,初期冲刷效应越明显;这是因为随着堵塞进程发展,透水砖内部孔隙空间减小,表面颗粒物在透水砖内部向下迁移能力减弱,径流冲刷携带的颗粒物量增加[26],同时堵塞引起透水砖入渗量减小,间接引起径流量增大对颗粒物冲刷作用加剧。


(a) 3年一遇
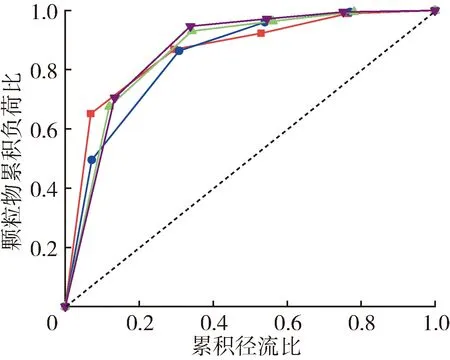
(b) 10年一遇图3 不同降雨重现期时各堵塞程度透水砖径流颗粒物M(V)曲线Fig.3 M(V) curves of runoff particles in permeable brickwith different blocking degrees under differentrainfall return periods

表1 不同降雨重现期时各堵塞程度透水砖径流颗粒物F30值Table 1 F30 values of runoff particles in permeable brickwith different blocking degrees under differentrainfall return periods
2.1.2不同堵塞程度透水砖表面径流颗粒物冲刷模型
应用指数冲刷模型对颗粒物累积冲刷质量随径流历时变化进行模拟,结果如图4所示。


(a) r=20%

(b) r=50%

(c) r=70%

(d) r=90%图4 不同降雨重现期下各堵塞程度透水砖径流颗粒物指数冲刷模型模拟结果Fig.4 Simulation results of exponential scouring model of runoff particles in permeable brick with different blockingdegrees under different rainfall return periods
由图4可见,指数冲刷模型可较好地描述不同堵塞程度透水砖径流颗粒物冲刷过程(R2均大于0.84),堵塞程度和降雨重现期均未对拟合曲线趋势产生太大影响。随径流历时增加,虽然径流中颗粒物累积冲刷质量不断增加,但颗粒物冲刷速率不断减小,说明冲刷强度逐渐减弱,20 min后颗粒物冲刷质量基本达到稳定。此外,发现透水砖堵塞程度越高、降雨重现期越大,径流初期(10 min以内)颗粒物冲刷速率越大,说明径流初期颗粒物冲刷强度较大、初期冲刷效应更强烈,这与M(V)曲线法和F30参数法分析结果一致。
相同堵塞程度时,降雨重现期越大,透水砖表面径流颗粒物冲刷质量越多,如堵塞程度为20%时,10年一遇降雨条件下径流颗粒物冲刷质量为3年一遇的4倍以上。同一降雨重现期下,随堵塞程度增加透水砖表面径流颗粒物冲刷质量逐渐增加;如降雨重现期为10年一遇时,堵塞程度为90%的场次降雨径流中颗粒物冲刷质量为堵塞程度为20%的10倍以上。可见,透水砖堵塞程度与降雨重现期不仅影响其表面径流颗粒物初期冲刷效应,同时也会影响累积冲刷质量总体水平。
2.1.3基于透水砖堵塞程度的表面径流颗粒物冲刷模型
将不同堵塞程度透水砖径流颗粒物冲刷过程应用指数冲刷模型进行拟合,得到的拟合参数及相关系数见表2,其中3年一遇降雨强度较小,堵塞程度为0%、10%时未形成径流,因此无拟合数据。由表2可见,相同堵塞程度下,降雨重现期越大,拟合得到的M0值越大;在同一降雨重现期时,透水砖堵塞程度越高,拟合得到的M0值越大。这是由于透水砖堵塞颗粒物主要滞留于面层[8],堵塞程度越高,面层堵塞颗粒物滞留量越大,可供冲刷的颗粒物越多;且降雨强度越大,冲刷作用越明显,致使可供冲刷的M0值越大。
研究表明,系数k可表征冲刷效应强弱,受冲刷颗粒物粒径效应与径流水动力条件共同影响,即受颗粒物自身迁移能力与径流冲刷携带能力共同影响,表现为k随冲刷颗粒物粒径增大而减小、随径流量增加而增大。
由表2可见,相同堵塞程度下,降雨重现期增大引起径流量增加,拟合得到的系数k值增大,表明透水砖表面颗粒物冲刷作用较明显,这与2.1.1节的结论一致。而在同一降雨重现期时,系数k则随透水砖堵塞程度增加呈先减后增趋势;这是由于在堵塞初期透水砖孔隙较大,入渗性能较强导致径流量较小,同时大粒径颗粒物可进入透水砖内部,径流冲刷携带的多为截留于面层的小粒径颗粒物,使得粒径效应占主导,所以系数k较大;堵塞中期透水砖孔隙逐渐减小,径流量虽有所增加,但小粒径颗粒物更易于进入透水砖内部、大粒径颗粒难以进入而被冲刷,粒径效应的影响大于水动力增强作用,所以系数k减小;透水砖堵塞末期,孔隙堵塞明显引起表面径流量大幅增加,同时大、小粒径颗粒均难以进入透水砖内部而被冲刷,所以系数k较大。
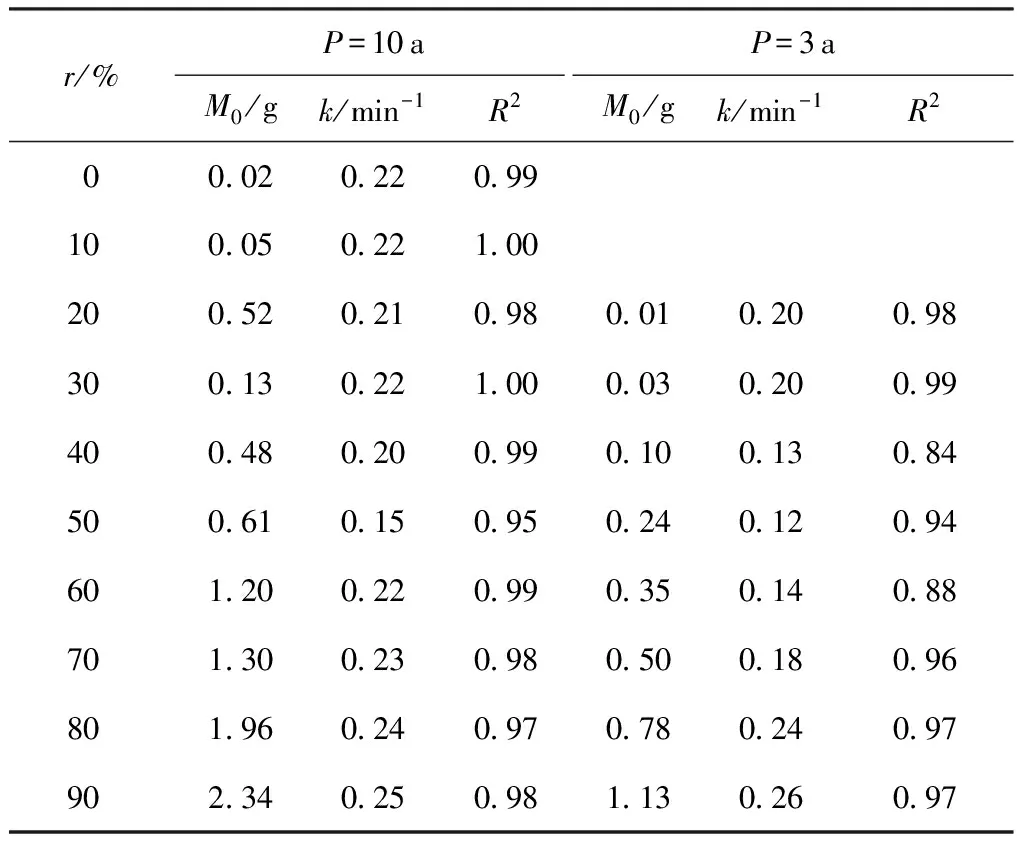
表2 透水砖径流颗粒物指数冲刷模型拟合参数Table 2 Fitting parameters of exponential scouring modelof runoff particles in permeable brick
由上可见,透水砖堵塞程度r与指数冲刷模型参数M0、k存在相关关系,因此将透水砖堵塞程度与模型参数进行拟合,分析指数冲刷模型参数与透水砖堵塞程度之间的定量关系,建立基于透水砖堵塞程度的表面径流颗粒物冲刷模型。透水砖堵塞程度与模型参数拟合曲线、拟合公式分别如图5和表3所示。
由图5可见,径流颗粒物指数冲刷模型参数M0和k与透水砖堵塞程度r具有显著相关性,相关系数较高;其中M0与透水砖堵塞程度r符合指数相关,k与透水砖堵塞程度r呈先降低后增加趋势。由表3可见,降雨重现期为3年一遇时,两个参数与透水砖堵塞程度r的拟合效果均优于降雨重现期为10年一遇;说明在降雨强度较小时以透水砖堵塞程度r为单一参数可以较好表达不同堵塞程度透水砖表面径流颗粒物冲刷规律。由此,当获知透水砖堵塞程度r时,便可快速预测不同堵塞程度透水砖径流颗粒物输出负荷。



(a) r与M0 (b) r与k图5 透水砖堵塞程度与径流颗粒物指数冲刷模型参数拟合关系Fig.5 Fitting relationship between blocking degree of permeable brick and parameters of exponential scouring model

表3 基于透水砖堵塞程度r的径流颗粒物指数冲刷修正模型Table 3 Modified exponential scouring model of runoff particles based on blocking degree of permeable brick
2.2 透水砖堵塞程度对径流输出颗粒物粒径分布的影响
2.2.1不同堵塞程度透水砖径流中颗粒物粒径分布
选取透水砖不同堵塞节点时所采集的各历时径流样品进行粒度分析,结果如图6所示。随径流历时变化,不同降雨重现期时各堵塞程度透水砖表面径流颗粒物粒径分布变化趋势一致:即粒径大于500 μm颗粒物体积占比随历时增加逐渐增加,而粒径小于150 μm颗粒物体积占比则随历时增加逐渐减少。这是由于透水砖表面初期径流量较小,冲刷携带的主要为小粒径颗粒物,而产流后期透水砖表面径流量增加对大粒径颗粒物冲刷携带能力增强所致。在堵塞中后期,降雨重现期为10年一遇时透水砖径流中,粒径大于500 μm颗粒物体积占比较3年一遇时有所增加,粒径小于150 μm颗粒物体积占比有所减少,说明降雨强度增大对大颗粒物冲刷增强作用更明显。在同一降雨重现期时,随堵塞程度增加,径流中粒径小于150 μm颗粒物体积占比明显提高。如3年一遇降雨条件时,堵塞程度由20%增加至90%,径流中粒径小于150 μm颗粒物在径流 5 min时的体积占比由33%增长至81%,粒径大于500 μm颗粒物体积占比由63%减少至16%,说明高堵塞程度下透水砖表面小粒径颗粒物冲刷作用更强。综上,堵塞程度、降雨重现期与径流历时均对透水砖径流中颗粒物粒径分布产生影响;堵塞程度增加导致透水砖径流中粒径小于150 μm颗粒物体积占比增加,而降雨重现期增大、径流历时增加均会引起粒径大于500 μm颗粒物体积占比增加。
2.2.2透水砖堵塞程度与冲刷颗粒物粒径分布相关性
为进一步识别透水砖堵塞程度与径流颗粒物粒径分布相关性,并明确降雨重现期、径流历时的作用,对透水砖堵塞程度与所采集不同历时径流中各粒径颗粒物体积占比进行相关性分析,结果如表4所示。由表4可见,在不考虑其他因素影响时,透水砖堵塞程度与径流中粒径小于150 μm颗粒物体积占比呈正相关关系,与径流中粒径大于500 μm颗粒物体积占比呈负相关关系。进一步考虑降雨重现期、径流历时因素影响,并进行偏相关分析,发现上述正相关、负相关系数绝对值均增大,表明以上两因素对透水砖堵塞程度与径流中粒径小于150 μm、大于500 μm颗粒物体积占比的相关性均具有增强作用,证明降雨重现期、径流历时确是影响径流颗粒物粒径分布的重要因素。结合2.2.1节来看,降雨重现期、径流历时因素的相关性增强作用效果与堵塞程度对粒径分布的影响效果相反,即降雨重现期越大、径流历时越长,会削弱堵塞程度的影响,导致径流中粒径小于150 μm颗粒物体积占比减少趋势更显著,而粒径大于500 μm颗粒物体积占比增加趋势更显著。由此得出,透水砖堵塞程度对径流中颗粒物粒径分布的影响受降雨重现期、径流历时因素牵制,存在交互作用,并非简单的同向加和作用。


(a) r=20% (b) r=50%
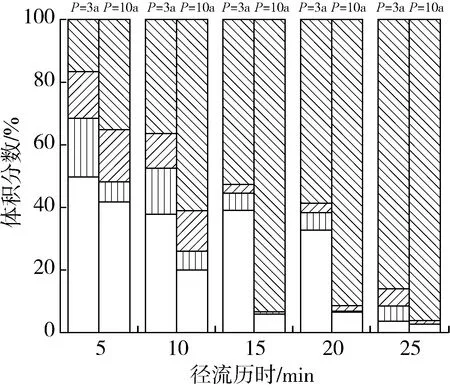

(c) r=70% (d) r=90%图6 不同降雨重现期时各堵塞程度透水砖径流颗粒物粒径变化Fig.6 Change of particle size in permeable brick runoff with different blocking degreesunder different rainfall return periods

表4 堵塞程度和不同粒径颗粒物体积占比相关性分析Table 4 Correlation analysis between blocking degree and volume proportion of particles with different particle sizes
3 结 论
透水砖系统的“面层累积-垂直堵塞-径流冲刷”颗粒物迁移模式与传统不透水下垫面简单的“表面累积-径流冲刷”模式不同;透水砖堵塞全过程动态变化持续影响表面径流中颗粒物冲刷质量、粒径分布,使其冲刷规律较不透水下垫面存在较大差异。本文主要结论有:
a.堵塞程度、降雨重现期会影响透水砖表面径流颗粒物初期冲刷效应,透水砖堵塞程度越高、降雨重现期越大,径流颗粒物的初期冲刷效应越明显。
b.指数冲刷模型可较好地描述各堵塞节点时透水砖径流颗粒物冲刷过程,将堵塞程度这一动态变化量引入传统指数冲刷模型,建立了基于透水砖堵塞程度的透水砖表面径流颗粒物冲刷模型。
c.透水砖堵塞程度可显著影响径流中颗粒物粒径分布,且与降雨重现期、径流历时存在交互影响作用;堵塞程度增加导致透水砖径流中粒径小于150 μm颗粒物体积占比增加,而降雨重现期增大、径流历时增加则会引起粒径大于500 μm颗粒物体积占比增加。

