三元混合气体燃料爆炸特性实验研究

韦双明，余明高，2，裴蓓，李世梁，康亚祥，徐梦娇，郭佳琪

（1 河南理工大学安全科学与工程学院，河南 焦作 454003； 2 重庆大学煤矿灾害动力学与控制国家重点实验室，重庆 400044）

引 言

清洁能源的应用不仅有助于解决能源安全问题[1]，对“碳达峰、碳中和”也有重要意义。二甲醚(DME)和甲烷(CH4)是常见的清洁能源，且其来源广泛，可以由石油、天然气、煤炭、生物质和废物等原料转化产生[2]。DME/CH4混合燃料可应用于发动机中，与传统柴油机相比，混合燃料发动机NOx排放可以大大减少[3]。但是，DME/CH4混合燃料层流燃烧速度较低，限制了其在发动机中的高效利用。氢气(H2)是一种清洁的气体燃料，具有较高的层流燃烧速度，研究发现在DME/CH4混合燃料中添加H2可以明显改善其燃烧性能[4]。然而H2具有较低的点火能量(约0.02 mJ)和较宽的爆炸极限(4%～75%)[5]。目前，储罐是储存可燃气体的常用载体，若H2/DME/CH4混合燃料在储存和运输过程中发生泄漏且遇到火源时便会发生严重爆炸事故。因此，有必要研究H2/DME/CH4混合燃料爆炸特性以保证其安全储存和运输。

国内外学者对H2、CH4、DME单一可燃性气体的爆炸特性进行了广泛研究。Zhang 等[6]实验和模拟研究了球形压力容器中H2/air 预混气的爆炸特性，揭示了初始压力对爆炸压力、压力上升速率及爆炸场的影响。Zheng 等[7]用透明管道分析了点火位置和当量比对预混H2/air 混合物爆炸特性的影响，深刻阐释了火焰结构和爆炸超压的变化规律。Xiao等[8-12]在管道中研究了H2/air 预混气的火焰传播特性，对“郁金香火焰”发展过程及火焰加速行为进行了深刻分析。时高龙等[13]对CH4/O2/N2预混气体爆炸火焰与压力的耦合振荡特性进行了研究，得到爆炸火焰与压力耦合振荡规律。余明高等[14]用管道探究了障碍物阻塞率梯度对CH4爆炸特性的影响，表明障碍物阻塞率梯度对CH4爆炸特性具有重要影响。罗振敏等[15-17]针对多元可燃气体对CH4爆炸特性及化学反应动力学进行了系统性研究。谭迎新等[18]在进行CH4/air 混合物爆炸传播研究中发现，在密闭空间内爆炸最大压力不受点火位置的影响。而Tomizuka 等[19]对DME/air 预混气湍流火焰速度进行了模拟研究。

此外，学者们还对H2/CH4和DME/CH4二元混合燃料爆炸特性进行了研究。Li等[20]研究了氢气体积分数和初始压力对H2/CH4/air 混合燃料爆炸特性的影响，指出添加H2会增大最大压力上升速率。Zheng 等[21-25]实验和模拟研究了H2添加对CH4/air 预混气火焰传播特性的影响，表明H2添加会影响火焰形状。Zhang 等[26]用定容燃烧弹系统研究了DME/CH4混合燃料在空气中的爆炸特性，研究表明混合燃料中二甲醚组分的增加会增大最大爆炸压力和最大压力上升速率。

虽然国内外学者在可燃气体爆炸特性研究方面取得了丰富的研究成果，但是这些研究主要针对单一可燃气体和二元可燃气体。近年来，少数学者对H2/DME/CH4三元混合气体的层流火焰速度进行了研究[4,27]，而对爆炸特性研究较少，其爆炸特性参数：爆炸压力峰值、最大压力上升速率及燃烧时间比较缺乏。事实上，三元混合气体相比于单一气体和二元混合气体的爆炸特性更为复杂，影响因素更多，需要引起足够重视。本文旨在利用定容燃烧弹研究各组分浓度及当量比对H2/DME/CH4/air预混气爆炸特性的影响，进而得到爆炸特性参数的变化规律，为H2/DME/CH4三元混合气体储存装置安全设计提供理论指导。

1 实验设计

1.1 实验装置

实验在标准20 L 球形爆炸装置中完成，实验装置如图1所示，主要由定容燃烧弹、点火系统、配气系统及数据采集系统等组成。定容燃烧弹是有效容积为20 L的球形容器，耐压能力可达20 MPa，在定容燃烧弹的壁面上对称安装着两块直径为110 mm、厚度为50 mm 的圆形石英玻璃，为纹影仪提供光学通道以便观察火焰发展过程。点火系统包括电火花发生器和点火电极，点火能量设定为1.0 J，电极直径和间距分别为1.5 mm和1.0 mm。配气系统包括真空泵和高压气瓶。数据采集系统包括高速相机、压力传感器和计算机，高速相机型号为Speed Sense VEO 710，拍摄速度根据火焰传播速度的不同设置为5000～7000 帧/s，图像分辨率最大为1280×800；爆炸压力采用PMC131G 型压力传感器进行采集，量程为-0.1～2.0 MPa，采集频率和精度分别为5000 Hz、0.1%。

图1 实验装置图Fig.1 Experimental setup

1.2 实验工况及方法

本实验主要对比研究H2/DME/CH4混合燃料各组分浓度及当量比对爆炸特性的影响。为方便研究，本文将混合燃料中各组分浓度定义为X(XH2、XDME、XCH4)，可用式(1)进行表示

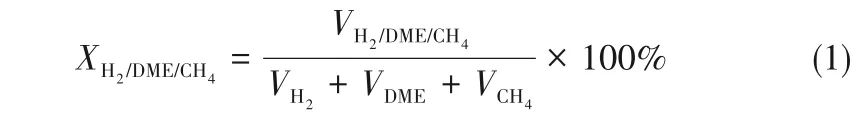
式中，VH2、VDME、VCH4分别代表混合燃料中H2、DME、CH4的体积。需要指出的是，为系统研究各组分浓度对爆炸特性的影响，本文将X设置为0～90%，间隔为10%，此时另外两种组分的体积之比设置为固定值1∶1。

当量比可用式(2)计算

式中，(F/A)是燃空比的实际值，(F/A)stoic是燃空比的化学当量比值。本文当量比设置为0.6、0.8、1.0、1.2、1.4及1.6，其中，φ=1.0为化学当量浓度。

在实验开始前首先检查装置气密性，以保证气密性良好。用真空泵将定容燃烧弹抽真空，根据道尔顿分压定律依次通入所需的燃料和空气，所有气体纯度均大于等于99.9%。需要注意的是在通气过程中要将通气电磁阀流量调整至合适大小，以免形成强湍流对实验结果造成影响。点火信号同步触发高速相机和压力传感器采集火焰图像和爆炸压力。实验结束后将定容燃烧弹内产生的废气排出准备下次实验。为保证实验准确性和可重复性，每个工况均至少进行三次重复实验。

2 实验结果与分析

2.1 火焰传播特性分析

图2所示为当量比为1时不同H2/DME/CH4组分浓度下的球形火焰传播纹影图像。由于视窗观察范围有限，本文仅对火焰边缘未达到视窗边界时的火焰传播特性进行分析。如图所示，在所有工况下，当H2/DME/CH4/air预混气被点燃后，球形火焰以层流状态向外传播，火焰半径逐渐增大，这不受混合气组分浓度变化的影响。但是，火焰传播速度则深受混合气组分浓度变化的影响。如图2(a)所示，随着混合气中氢气浓度XH2的增加，点火后相同时刻的火焰半径逐渐变大。比如，当XH2=90%时，点火后5 ms 时的球形火焰正好达到视窗边界，而对于XH2=0 而言，点火后5 ms 时的球形火焰依然很小。这表明球形火焰传播速度随着XH2的增加而明显增加。此外，还可以看出随着XH2的增加，火焰表面的裂纹褶皱逐渐增多，最后这些裂纹褶皱形成了胞状结构，使其火焰胞状不稳定性增强。暴秀超等[28]对预混火焰胞状不稳定性进行了研究，指出火焰胞状不稳定性主要指热质扩散不稳定性和流体动力学不稳定性。此前研究表明对于化学当量比火焰，氢气的加入增强了H2/DME/CH4/air 预混火焰流体动力学不稳定性，而对热质扩散不稳定性影响不大，因此流体动力学不稳定性是造成胞状不稳定性增强的主要原因[4]。而对于XCH4和XDME而言，火焰传播速度则表现出相反的变化趋势。由图2(b)和(c)可以看出，随着XCH4和XDME的增加，点火后相同时刻的火焰半径均逐渐变小。这表明球形火焰传播速度随着XCH4和XDME的增加而降低。同时，火焰表面的裂纹褶皱随XCH4和XDME的增加在减少，即球形火焰表面变得更加光滑，胞状不稳定性在减弱。

图2 不同氢气/二甲醚/甲烷浓度下球形火焰传播纹影图像（φ=1.0）Fig.2 Schlieren images of spherical flame propagation under different hydrogen/dimethyl ether/methane concentrations(φ=1.0)

为了深入研究H2/DME/CH4组分浓度变化对火焰传播特性的影响，本文引入平均火焰传播速度Sa进行详细分析。如图3所示，Sa被定义为球形火焰半径r对点火时间拟合直线的斜率，以XH2=20%为例，可以看出Sa为3.34 m/s。本文是用等面积法计算r，此方法在文献[29]中已有详细介绍。

图3 平均火焰传播速度定义图（XH2=20%）Fig.3 Definition diagram of average flame propagation speed（XH2=20%）

图4 所示为H2/DME/CH4组分浓度对Sa的影响，由图可知，Sa随XH2的增加而增加，需要指出的是增长趋势并不一致，即可以分成两个增长阶段，在图4中用不同的颜色区分不同的阶段。在第Ⅰ阶段(0≤XH2≤50%)，Sa随着XH2的增加而线性增加，增加较为缓慢；而到了第Ⅱ阶段(50%≤XH2≤90%)，Sa随着XH2的增加而快速增加，并非线性增长关系，这表明XH2对Sa的影响存在转折点，转折点为XH2=50%。对于XDME而言，Sa随着XDME的增加而减小，这与XH2的变化趋势相反，而与XH2类似的是其变化趋势也可分为两个阶段。在第Ⅰ阶段(0≤XDME≤50%)时，Sa随XDME的增加而线性减小；在第Ⅱ阶段(50%≤XDME≤90%)时，其变化趋势与第Ⅰ阶段类似，但减小得更为缓慢。综上所述，对于XH2与XDME而言，其变化趋势都存在两个阶段，其转折点都位于X=50%处。但是，Sa随XCH4的变化趋势则相对简单，即始终线性降低，并没有出现转折点。总体而言，Sa随XH2的增加而增加，而随XDME和XCH4的增加而减小。这是由于氢气相较于二甲醚和甲烷活泼性更强，氢气的加入增大了混合气体的热扩散系数，有利于气体内部热量的传播，增加了混合气体的燃烧速率和绝热火焰温度，促进了火焰传播。

图4 不同氢气/二甲醚/甲烷浓度下平均火焰传播速度变化曲线(φ=1.0)Fig.4 Variation curves of average flame propagation speed under different hydrogen/dimethyl ether methane concentrations(φ=1.0)

2.2 爆炸压力峰值pmax分析

压力峰值pmax是爆炸达到的最大压力，是表征爆炸强度的重要参数之一，研究混合气体组分浓度对爆炸压力峰值的影响具有重要意义。图5所示为氢气组分浓度对爆炸压力峰值的影响，可以看出，pmax与XH2总体上呈正相关关系，同时也深受当量比φ的影响。当φ=0.8、1.0 和1.2 时，pmax随XH2增加可以分为两个增长阶段，这与图4 中平均火焰传播速度的变化情况相似。在第Ⅰ阶段，XH2对pmax影响较小，基本呈线性相关关系；而到了第Ⅱ阶段后pmax急剧增加。同时，需要指出的是第Ⅰ阶段与第Ⅱ阶段的转折点也会随φ的变化而变化。比如，当φ=0.8 时，第Ⅰ阶段与第Ⅱ阶段的转折点Tφ=0.8为XH2=50%；当φ=1.0 时，第Ⅰ阶段与第Ⅱ阶段的转折点Tφ=1.0提前到XH2=40%；而当φ=1.2 时，第Ⅰ阶段与第Ⅱ阶段的转折点Tφ=1.2又推迟到XH2=60%。这表明在φ=1.0时，相对较少的H2便可引起pmax开始增加，同时也可以看出在此当量比下的pmax相比于其他当量比时更大，这在进行储存装置的安全设计时应该引起足够重视。而对于φ=0.6、1.4和1.6而言，并没有出现转折点，即pmax均随XH2的增加而线性增加。

图5 氢气浓度对爆炸压力峰值的影响Fig.5 Effect of hydrogen concentration on explosion peak pressure

然而，甲烷浓度XCH4对pmax的影响则与XH2有很大不同。图6 所示为XCH4对pmax的影响，由图可知在所有当量比下，pmax均随XCH4的增加线性降低。本文对pmax均随XCH4的变化情况进行了线性拟合，拟合关系可以用式(3)进行表征

图6 甲烷浓度对爆炸压力峰值的影响Fig.6 Effect of methane concentration on explosion peak pressure

其中，拟合参数如表1所示，可以看出在所有当量比下式(3)的斜率均为负值，这表明pmax与XCH4呈负相关关系，而下降速率则与当量比φ相关。即在φ=1.0 附近时，比如φ=0.8、1.0 及1.2 时，pmax随XCH4增加下降的较为缓慢；但是当远离φ=1.0 时，比如φ=0.6、1.4及1.6时，pmax则下降的较为快速。其中，当φ=1.6时，斜率的绝对值最大，这意味着φ=1.6 时的pmax下降最快，pmax在φ=1.6时对XCH4最为敏感。

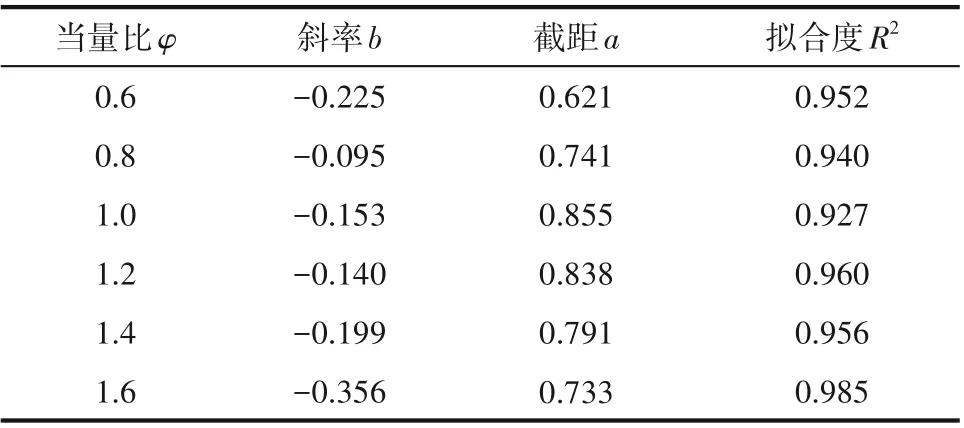
表1 式（3）的线性拟合参数Table 1 Linear fitting parameters of Eq.（3）

图7所示为二甲醚浓度XDME对不同当量比氢气/二甲醚/甲烷混合气体爆炸压力峰值的影响，根据pmax随XDME变化的特点，可将整个过程分为两个时期，分别为压力增长期和压力平台期。以φ=1.0 为例，当XDME≤50%时，pmax随XDME的增加而增加，这一时期可被称为压力增长期；但是当XDME≥50%时，XDME对pmax的影响不大，出现了“平台效应”，这一时期可被称为压力平台期。由此可见，XDME对pmax的影响并不一致，当XDME较低时，pmax与XDME呈正相关关系，而当XDME较高时，XDME对pmax的影响较小。

图7 二甲醚浓度对爆炸压力峰值的影响Fig.7 Effect of dimethyl ether concentration on explosion peak pressure

2.3 最大压力上升速率（dp/dt）max及爆炸指数KG分析

最大压力上升速率(dp/dt)max被定义为压力-时间曲线上升阶段斜率的最大值[30]，它也是衡量可燃气体爆炸强度的重要参数。为了消除燃烧室形状对(dp/dt)max的影响，学者们对(dp/dt)max与容器容积V的关系进行了深入研究，发现两者关系可用“三次方定律”表示[31]。

式中，KG为爆炸指数，单位为MPa·m/s。KG与燃料类型和初始条件有关，其数值可以用来表征爆炸强度大小，也可用于评估可燃气体爆炸后果和安全性[32]。数值越大说明该可燃气体在此工况下的爆炸强度越大，爆炸后果越严重[32]。需要指出的是(dp/dt)max与KG符合式(4)的关系，在本文中定容燃烧弹容积V为定值，因此二者具有相同的变化趋势，并将其显示在同一图中。为分析当量比对(dp/dt)max及KG的影响，本文选取X=50%进行分析。图8 所示为当X=50%时，(dp/dt)max及KG随当量比的变化关系。由图可知，当X=50%时，(dp/dt)max在φ=1.0时取得最大值，随着当量比逐渐偏离φ=1.0，(dp/dt)max明显减小。这是由于当φ<1.0 时，燃烧室中的燃料不足，空气过剩；而当φ>1.0 时，燃烧室中的空气不足，燃料过剩，这都会降低燃烧产生的热量，导致爆炸压力降低[30]。此外，前期研究表明H2/DME/CH4混合燃料在φ=1.0附近的层流燃烧速度最快，随着当量比逐渐偏离φ=1.0，层流燃烧速度也在明显减小[4]，这会增加混合气体的反应时间。以上两方面因素共同导致了压力上升速率的降低。

图8 最大压力上升速率及爆炸指数随当量比的变化关系Fig.8 Variation of maximum pressure rise rate and explosion index with equivalence ratio

图9所示为各组分浓度X对(dp/dt)max及KG的影响曲线，由图可知，各组分浓度X对(dp/dt)max及KG的影响明显不同。对于XH2而言[图9（a）]，(dp/dt)max及KG同时受XH2和φ的强烈影响。首先对于φ=0.8、1.0 和1.2工况，(dp/dt)max的变化趋势均可以分为两个阶段，当XH2较小时(XH2≤60%)，XH2对(dp/dt)max的影响不大，但是当XH2较大时(XH2≥60%)，(dp/dt)max则随XH2急剧增加。以φ=1.0为例，XH2=90%的最大压力上升速率为1508.88 MPa/s，相比于XH2=60%大幅增加了1511.12%，而XH2=60%的最大压力上升速率相比于XH2=0 只增加了68.56%，增长趋势明显变缓，这表明只有当XH2增加到一定浓度时(dp/dt)max才会明显受到XH2的影响。与φ=0.8、1.0和1.2不同，当φ=0.6、1.4和1.6时，(dp/dt)max随XH2的增加变化较小，这表明在这三种当量比下，(dp/dt)max对XH2并不敏感。

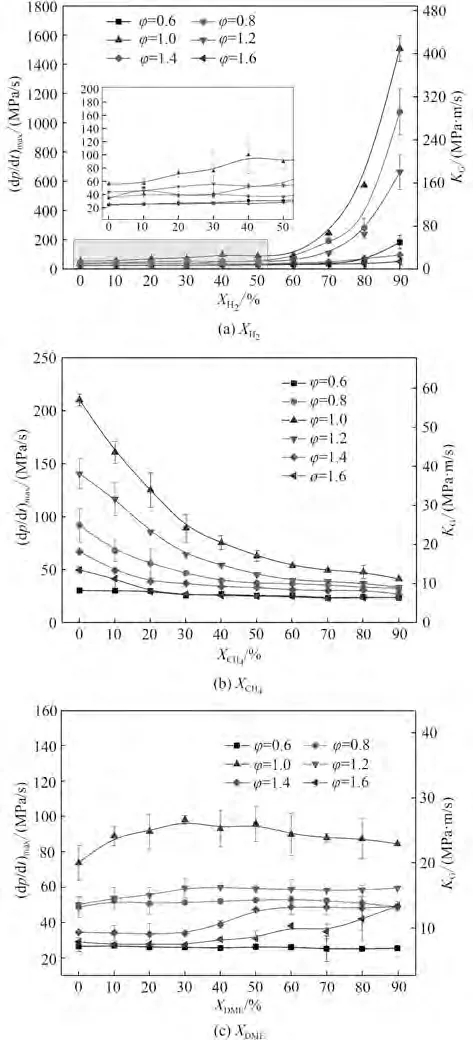
图9 组分浓度对最大压力上升速率及爆炸指数的影响Fig.9 Influence of component concentration on maximum pressure rise rate and explosion index

对于XCH4而言[图9（b）]，与XH2相似的是，(dp/dt)max及KG也受XCH4和φ的强烈影响。在所有当量比下，(dp/dt)max均随XCH4的增加单调递减，但是(dp/dt)max的下降速率受到φ的强烈影响。相比于XCH4=0，当XCH4=90%时，φ=0.6、0.8、1.0、1.2、1.4及1.6的(dp/dt)max分别下降了22.91%、64.68%、80.38%、76.19%、59.75%和52.12%。可以看出当φ=1.0时，(dp/dt)max下降最快，当φ逐渐偏离1.0 时，(dp/dt)max下降越来越慢，其中，φ=0.6 时下降最慢。这表明当φ=1.0 时，(dp/dt)max对XCH4最为敏感，随着φ逐渐偏离于1.0，(dp/dt)max对XCH4敏感性变弱，φ=0.6 时的敏感性最弱。对于XDME而言[图8（c）]，随着XDME的增加，(dp/dt)max的变化规律不明显，这与XH2和XCH4的情况明显不同。

同时从图9可以看出爆炸指数受到了混合气体组分变化和当量比的强烈影响。在高氢气组分、低甲烷组分及化学当量比下的爆炸指数相对较大，这意味着这些工况下的爆炸危险性较高，在进行储存容器的安全设计时应该予以高度重视。

2.4 燃烧时间tc

Xu等[33]对可燃气体燃烧时间tc进行了研究，tc被定义为点火时刻与到达压力峰值时刻的时间间隔[34-35]。图10所示为燃烧时间随各组分浓度的变化关系，由图10(a)可知，在所有当量比下，tc随XH2的增加而线性递减。为了定量表征在不同当量比下tc随XH2的线性关系，本文对其进行了线性拟合，拟合方程可表示为

表2给出了式(5)的线性拟合参数，可以看出不同当量比下式(5)的拟合度R2≥0.94，意味着tc与XH2具有较好的线性关系。此外，线性方程的斜率d均为负值，说明tc与XH2呈负相关关系，前期研究表明氢气组分的增加会增大混合气体的层流燃烧速度[4]，这会增大单位时间内混合气体的消耗速率，进而降低燃烧时间[33]。Tran 等[36]在研究合成气/空气混合物的爆炸特性中也得出了相似的结论，发现提高合成气中氢气的比例可以降低燃烧时间。需要注意的是斜率的绝对值随着当量比的增加先减小后增大，在φ=1.0时取得最小值，这表明随着当量比的增加，tc对XH2的敏感性先变弱后增强，在φ=1.0时敏感性最弱。

表2 式（5）的线性拟合参数Table 2 Linear fitting parameters of Eq.（5）

由图10(b)可知，所有当量比下的tc随着XCH4的增加而线性增加，其关系可用以下拟合方程表示

图10 组分浓度对燃烧时间的影响Fig.10 Effect of component concentration on combustion duration

表3 给出了式(6)的线性拟合参数，可以看出式(6)的斜率f均为正数，表明tc与XCH4呈正相关关系，这与tc和XH2的负相关关系相反。Wang 等[27]对H2/DME/CH4/air 混合物的层流燃烧速度进行了研究，发现混合物中甲烷组分的增加会导致层流燃烧速度的降低，这会降低燃料的消耗速率，继而增加燃烧时间。此外，随着当量比的增加，线性拟合方程的斜率f先减小后增加，在φ=1.0 时取得最小值51.30，表明tc对XCH4的敏感性先变弱后增强，且在φ=1.0 时敏感性最弱，这与tc对XH2的敏感性变化相同。

表3 式（6）的线性拟合参数Table 3 Linear fitting parameters of Eq.（6）

相比于XH2、XCH4与tc的线性关系，XDME对tc的影响则更为复杂，如图10(c)所示，tc随XDME的变化关系与φ有关。当φ=0.6和1.6时，tc随着XDME的增加先增大后减小，分别在XDME=20%和40%时取得最大值。然而，当φ=0.8、1.0、1.2 及1.4 时，tc随XDME的增加变化不大，几乎不受XDME的影响。

3 结 论

本文通过研究组分浓度和当量比对氢气/二甲醚/甲烷/空气混合物爆炸特性的影响，得到以下主要结论。

(1)平均火焰传播速度随XH2的增加而增加，随XDME的增加而降低，且都存在转折点；平均火焰传播速度随XCH4的增加线性降低，但是并不存在转折点。

(2)压力峰值受XH2及φ的共同影响，当φ在1.0附近时，压力峰值可以分为两个阶段，而当φ远离1.0 时，压力峰值线性增加；压力峰值随XCH4的增加线性降低，同时，随XDME的增加压力峰值可以分为两个时期。

(3)XH2对最大压力上升速率具有积极影响，而XCH4则对最大压力上升速率具有消极影响，XDME对最大压力上升速率的影响不大。高氢气浓度、低甲烷浓度及化学当量比下的工况爆炸指数较大，在进行安全设计时应该予以重视。

(4) 燃烧时间随XH2的增加线性降低，而随XCH4的增加线性增加，其线性关系均可用线性拟合方程进行表征。而XDME对燃烧时间的影响更为复杂，燃烧时间与XDME的关系与φ有关。