反向旋转卧式双轴捏合反应器混合特性的数值模拟
成文凯,张先明,王嘉骏,冯连芳
(1 浙江理工大学材料科学与工程学院,纺织纤维材料与加工技术国家地方联合工程实验室,浙江 杭州 310018;2 浙江大学化学工程与生物工程学院,化学工程联合国家重点实验室,浙江 杭州 310027)
引 言
聚合物在制备过程中存在高黏、变黏等特征,且具有复杂的流变特性,严重制约着聚合体系的流动、混合、传热以及传质等过程,因此通常需要借助于特殊的搅拌设备。卧式双轴圆盘反应器具有较大的工作容积和热交换表面,但几乎没有捏合效果和自清洁特性。双螺杆挤出机具有良好的自清洁特性,但反应空间非常有限,剪切作用强,物料的停留时间很短。德国Bayer[1-7]、德国BASF[8]和瑞士List[9-14]等公司开发了新型的卧式双轴捏合反应器,这种搅拌设备结合了圆盘反应器和双螺杆挤出机两种搅拌结构的特征[15-16],具有大的反应空间,优异的混合性能、传热性能以及表面更新性能,且具备良好的自清洁能力,因此在本体聚合、缩合聚合和聚合物脱挥等领域具有较好的应用前景[17-19]。但是,卧式捏合反应器的专利技术均为国外企业所垄断,相关研究亟待开展。
由于捏合反应器的几何结构复杂,桨叶在重叠区域存在交错,因此相关的研究非常有限。冯连芳等[20-21]通过实验方法研究了卧式双轴T 型搅拌器在牛顿流体和非牛顿流体中的搅拌功率特性。冯慧生课题组[22-25]通过计算流体力学(computational fluid dynamics,CFD)模拟方法研究卧式双轴搅拌设备的均相、气液两相以及固液两相的湍流流动过程,获取了流速、搅拌功率和停留时间分布等信息,考察了搅拌转速、进料流量与搅拌结构等因素的影响规律,但其研究体系主要为低黏湍流过程。Seck 等[26]以高黏度硅油为实验物料,通过实验方法研究了同向旋转卧式双轴捏合机的混合和脱挥性能,定义了Bond 数来判定物料在反应器中的轴向返混情况。单喜良等[27]采用离散元方法对三维List 卧式差动双轴搅拌设备内高密度聚乙烯(HDPE)填充碳酸钙复合材料的混合过程进行了模拟,研究了加料速率和转速对物料充满度、停留时间分布及混合均匀程度的影响。叶阳[28]设计了一种带有沿径向分布双层捏合棒的卧式双轴自清洁反应器,采用三维有限元(finite element method,FEM)方法模拟了高黏牛顿流体的层流流动过程,并且分析了这种搅拌设备的分布混合过程与混合效率。Cheng 等[29-30]采用可视化实验研究和CFD 数值模拟方法相结合的方法揭示了卧式双轴捏合反应器的流动成膜机理,并且采用CO2在糖浆中等速吸收的方法来测定反应器的容积传质系数,考察了物料黏度、搅拌转速以及桨叶结构等因素的影响。研究表明,捏合反应器的传质性能优于圆盘反应器,这归因于捏合反应器独特的成膜机理与表面更新性能。Cheng 等[31]采用有限元方法模拟了高黏糖浆在同向同速旋转的卧式双轴捏合反应器中的层流流动过程,进一步采用粒子示踪技术分析了捏合反应器的整体与局部分布混合过程,并且评价了其混合效率。研究发现,捏合反应器几乎不存在轴向推动力,捏合杆可以强化径向混合过程。Cheng 等[32]通过有限元数值模拟分析了差速反向旋转卧式双轴捏合反应器中的混合过程原理,但并未探讨搅拌结构对流动与混合过程的影响规律。
因此,本文以差速反向旋转的卧式双轴捏合反应器为研究对象,高黏度牛顿流体糖浆为模拟物料,采用FEM 数值模拟方法获取高黏糖浆在捏合反应器中的层流流动过程,得到流速和剪切速率的空间分布,并且结合粒子示踪技术分析其分布混合过程以及混合效率,探究搅拌结构对流动与混合过程的影响规律,进而可以揭示混合过程强化的方法与手段。研究结果可为反向旋转卧式双轴捏合反应器的优化设计提供理论基础和指导思路。
1 三维有限元数值模拟
1.1 卧式双轴捏合反应器的几何构型
为了研究搅拌结构对捏合反应器流动与混合过程的影响规律,设计了六种不同结构的差速反向旋转卧式双轴捏合反应器(opposite-rotating twin-shaft kneader,OPK),如图1所示。不同结构的捏合杆如图2所示,捏合杆侧边的长度分别为7 mm、15 mm 和23 mm。根据搅拌结构将六种捏合反应器分别定义为OPK24-15 mm[图1(a)]、OPK36-15 mm[图1(b)]、OPK48-15 mm[图1(c)]、OPK24-7 mm[图1(d)]、OPK24-23 mm[图1(e)]和OPK24-disk-15 mm[图1(f)],其搅拌结构和搅拌转速如表1 所示。OPK24-15 mm、OPK36-15 mm 和OPK48-15 mm 三者的捏合杆数目不同,捏合杆的结构相同[图2(b)]。OPK24-7 mm、OPK24-15 mm 和OPK24-23 mm 三者的捏合杆数目相同,捏合杆的结构分别如图2(a)~(c)所示。OPK24-15 mm 和OPK24-disk-15 mm 的捏合杆数目和结构相同,但OPK24-disk-15 mm 的桨叶中包含一个光滑圆盘。左侧搅拌轴的旋转方向为顺时针,右侧搅拌轴的旋转方向为逆时针。左右两侧搅拌单元的捏合杆数目之比和搅拌转速呈反比。左右两侧搅拌轴的转速分别为60 r/min 和30 r/min。搅拌釜、搅拌轴以及桨叶的直径分别为140 mm、40 mm 和130 mm。左右两个搅拌轴的中心距为90 mm。单个搅拌轴轴向上相邻两个桨叶的中心距为60 mm。OPK24-disk-15 mm 中圆盘的直径和厚度分别为110 mm和5 mm。为了避免桨叶之间产生机械干涉,左右两侧桨叶之间的初始相位角均为0°。

图2 不同结构的捏合杆示意图Fig.2 Schematic sketch of different kneading bars

表1 卧式双轴捏合反应器Table 1 Different horizontal twin-shaft kneaders

图1 卧式双轴捏合反应器示意图Fig.1 Schematic sketch of horizontal twin-shaft kneaders
1.2 控制方程
高黏牛顿流体糖浆在捏合反应器中的流动近似为不可压缩的等温层流流动。
连续性方程为:
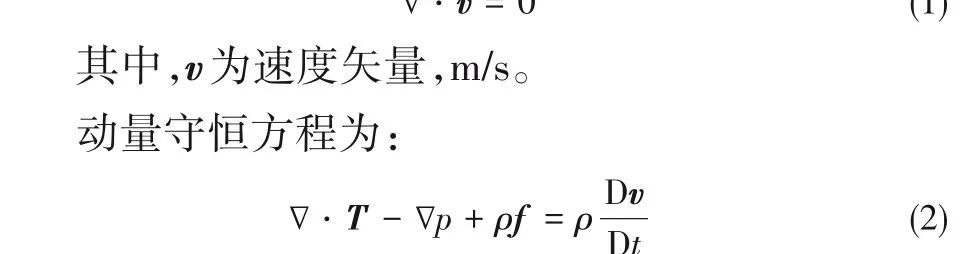
其中,T、p、ρ、t和f分别表示额外应力张量、压力(Pa)、流体密度(kg/m3)、时间(s)和体积力(N)。
卧式双轴捏合反应器运动过程复杂,因而采用网格叠加技术(mesh superposition technique,MST)来进行模拟双轴的搅拌运动[33-34]。在一定的时间间隔内分别对流道和搅拌桨叶划分网格,然后将这两部分网格进行组合。流道和搅拌桨叶有部分网格重合,在模拟过程中通过坐标变换来判定流道网格、搅拌桨叶网格以及两者共有网格。因此,动量守恒方程变为如下形式:

当网格点为流体域时,H=0;当网格点为搅拌结构时,H=1,此处的速度为搅拌结构的转速vp(m/s)。
1.3 计算域网格划分
卧式双轴捏合反应器的计算域如图1(a)所示。采用Gambit 2.3 软件分别对流道和搅拌桨叶进行网格划分,得到的六面体结构化网格如图3 所示。捏合反应器的壁面和重叠区域的网格进行加密[图3(a)]。对OPK24-15 mm 划分不同数目的网格进行网格无关性验证,分别为119550、144000 和210550。选取与搅拌轴平行的一条直线[图1(a)]来分析网格数目对局部流速的影响,如图4 所示。该直线的两个点的坐标分别为(-0.08 m,0 m,0 m)和(-0.08 m,0 m,0.075 m)。可以发现,当网格数目大于144000 时,流速几乎不发生变化。因此,数值模拟中OPK24-15 mm[图3(b)]、OPK36-15 mm[图3(c)]、OPK48-15 mm[图3(d)]、OPK24-7 mm[图3(e)]、OPK24-23 mm[图3(f)]和OPK24-disk-15 mm[图3(g)]的网格数目分别为144000、156150、168300、141120、146880和275765。
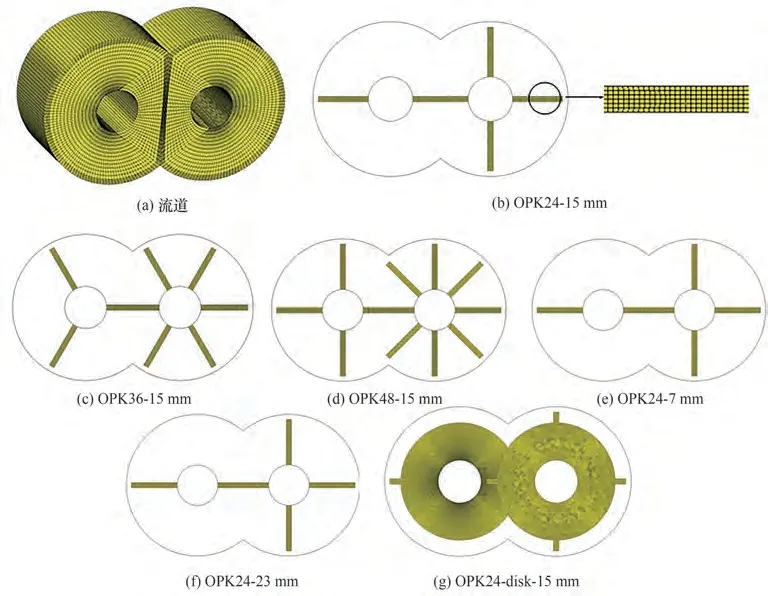
图3 计算网格示意图Fig.3 Schematic sketch of computational grid
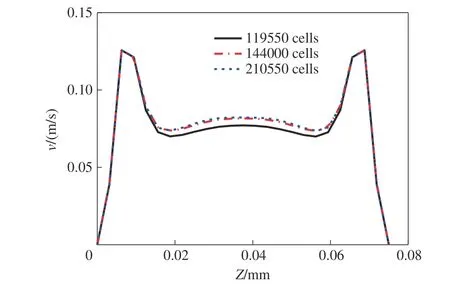
图4 网格数目对OPK24-15 mm局部速度的影响Fig.4 Effect of number of cells on local velocity magnitude on Line 1 in OPK24-15 mm(t=1 s)
1.4 边界条件与模拟策略
采用计算流体力学Polyflow 3.10.2 软件来模拟卧式双轴捏合反应器中的间歇等温层流流动过程,考虑重力和惯性。选取的物料为高黏糖浆(牛顿流体),其黏度为68 Pa⋅s,密度为1472 kg/m3。反应器壁面和搅拌桨叶表面均采用无滑移边界条件,借助于网格叠加技术(MST)来模拟双轴的旋转运动。
1.5 混合过程表征
通过粒子示踪技术剖析捏合反应器中的混合过程。示踪粒子存在如下假设:忽略粒子的质量以及粒子之间的相互作用;示踪粒子不影响反应器中的流场,其运动过程只依赖于速度场。
Eulerian速度场为:

当t=0 s 时,x=x(x0,y0,z0)。在局部坐标中,采用4 阶显式Runge-Kutta 程序,从t=0 s 开始,在很短的时间间隔内对式(5)进行积分来确定粒子的新位置,接着以该位置为起点求解示踪粒子的新位置,重复上述步骤直至相应的计算要求。
Danckwerts[35]使用分离尺度Ls(m)来定量表征反应器中的混合过程,其表达式为:

相关系数R(r,t)的取值范围为[-1,1],值为-1 表示距离为r两个粒子的浓度完全相反(一个粒子点为纯的连续相,另一个粒子点为纯的分散相),值为1表示距离为r两个粒子的浓度相同(两个粒子点为纯的连续相或者分散相)[33-34]。
通过动力学方法来追踪流体单元在运动过程中线、面或体变形,进而可以表征反应器的分布混合性能[36]。
拉伸率为:
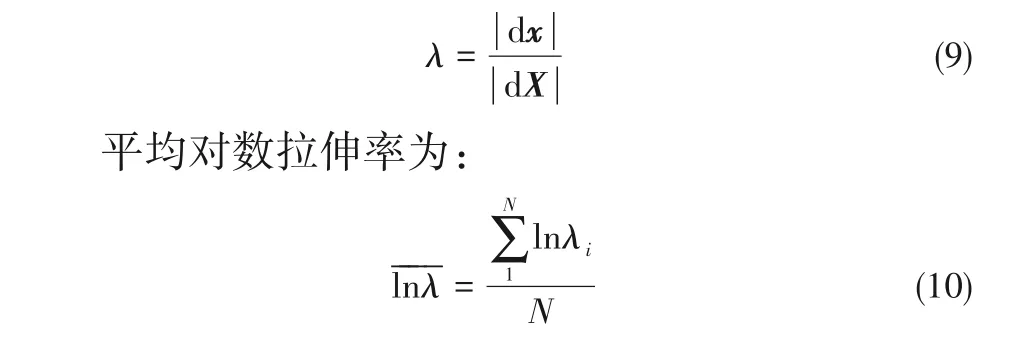
其中,N为示踪粒子的数目。
瞬时混合效率定量地表征了混合过程中的拉伸速率[33-34],其取值范围为[-1,1],值为-1 表示所有耗散的能量都用于缩短材料线的长度,而值为1 表示所有耗散的能量都用于拉伸材料线。瞬时混合效率的表达式为:
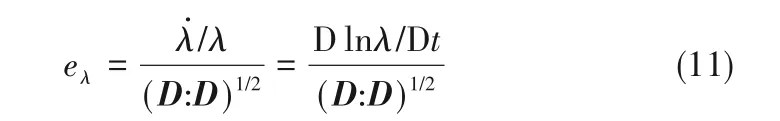
其中,D为应变速率张量,是速度梯度张量的对称部分。
平均瞬时混合效率为:

2 结果与讨论
2.1 流体动力学
图5为三种捏合反应器在Z=0.0525 m平面上速度矢量图。可以看出,捏合反应器中几乎无流动死区,左侧区域的流速高于右侧区域,桨叶末端和重叠区域的流速较高,桨叶在重叠区域存在周期性的捏合作用。

图5 Z=0.0525 m平面上速度矢量图Fig.5 Velocity vectors on plane Z=0.0525 m
图6 和图7 为不同平面的速度分布云图。左侧桨叶转速为右侧桨叶的两倍,因此左侧区域的流速高于右侧。两个搅拌轴附近区域的流速较小,桨叶末端和重叠区域的流速较大,且高速流动区域随着捏合杆数目和捏合杆长度的增加而增大。圆盘结构对流速分布的影响较小。

图6 Z=0.0525 m平面上速度分布云图Fig.6 Contours of velocity magnitude on plane Z=0.0525 m(t=1 s)
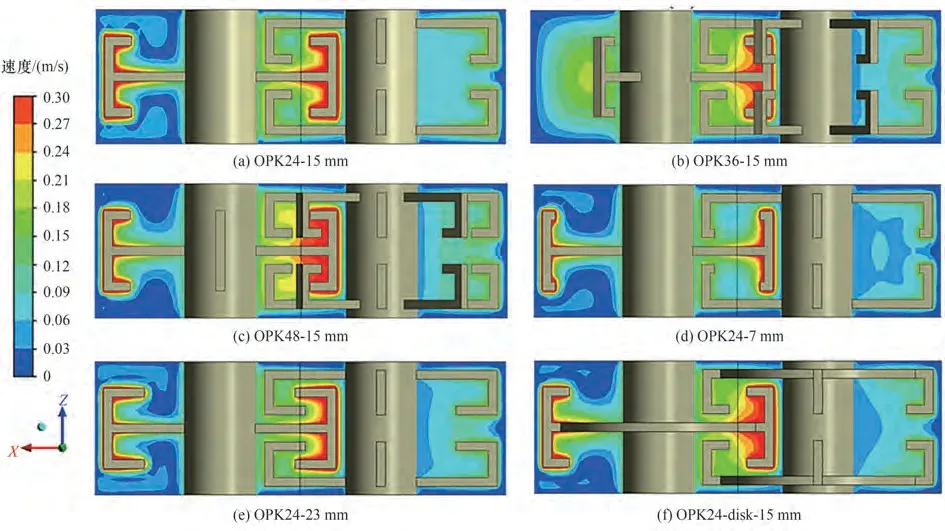
图7 Y=0 m平面上速度分布云图Fig.7 Contours of velocity magnitude on plane Y=0 m(t=1 s)
图8、图9分别为不同平面上局部剪切速率分布云图。由图可见,桨叶末端和重叠区域的剪切速率较大,且高剪切区域随着捏合杆数目的增加而逐渐增大(OPK48-15 mm>OPK36-15 mm>OPK24-15 mm)。桨叶间隙随着捏合杆的长度增加而减小,桨叶末端和重叠区域的速度梯度增加,因此剪切速率随着捏合杆长度的增加而增加(OPK24-23 mm>OPK24-15 mm>OPK24-7 mm)。圆盘对剪切速率的影响较小。

图8 Z=0.0525 m平面上剪切速率分布云图Fig.8 Contours of shear rate on plane Z=0.0525 m(t=1 s)
从图7 和图9 中还可以看出,桨叶末端与反应器壁面以及两个搅拌轴的间歇很小,同时搅拌桨叶在重叠区域存在捏合作用,搅拌桨叶可以相互清理,因此捏合反应器具有良好的自清洁性能,且随着捏合杆数目和捏合杆长度的增加而增强。
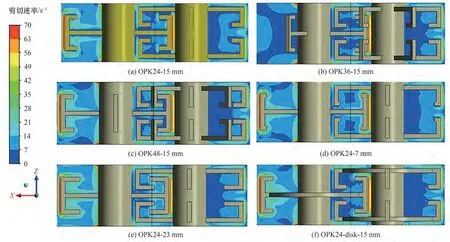
图9 Y=0 m平面上剪切速率分布云图Fig.9 Contours of shear rate on plane Y=0 m(t=1 s)
2.2 分布混合
搅拌结构对轴向分布混合过程的影响如图10所示。在捏合反应器中随机放置3000个材料点,左侧(-0.115 m 图10 轴向分布混合过程(右侧红色点浓度为1,左侧蓝色点浓度为0)Fig.10 Axial distributive mixing process x<0.115 m; -0.07 m 图11 搅拌结构对轴向分布混合分离尺度的影响Fig.11 Effect of kneader configuration on segregation scale for axial distributive mixing process 搅拌结构对径向分布混合过程的影响如图12所示。在捏合反应器中随机放置3000个材料点,左侧(0 m 随着捏合杆数目的增加,单位时间内在重叠区域捏合次数增加,可以推动更多的物料在捏合反应器左右两侧进行交换,更多的红色粒子从左侧区域运动到右侧区域,更多的蓝色粒子从右侧区域运动到左侧区域,因此分布混合过程的性能为:OPK48-15 mm>OPK36-15 mm>OPK24-15 mm。而捏合杆长度和圆盘对分布混合过程的影响较小。 搅拌结构对分离尺度的影响如图13 所示。随着捏合杆数目增加,单位时间内捏合次数增加,进而可以强化分布混合过程,因此分离尺度随着捏合杆数目的增加而减小。当混合时间为0~20 s 时,分离尺度下降的顺序为:OPK48-15 mm>OPK36-15 mm>OPK24-15 mm。当混合时间为20~60 s 时,OPK24-15 mm 的分离尺度最大,OPK48-15 mm 和OPK36-15 mm 的分离尺度差异较小。当捏合杆长度增加时,高流速和高剪切区域增加,可以推动更多的物料进行混合。因此,当混合时间为0~10 s时,OPK24-23 mm 的分离尺度最小,且下降的速度最快。当混合时间为10~60 s 时,OPK24-7 mm、OPK24-15 mm 和OPK24-23 mm 三者的分离尺度逐渐减小,且差异较小。圆盘对流速和剪切速率的影响较小,进而对分布混合过程的影响较小。因此,OPK24-15 mm 和OPK24-disk-15 mm 的分离尺度很接近。 图13 搅拌结构对径向分布混合过程分离尺度的影响Fig.13 Effect of kneader configuration on segregation scale for angular distributive mixing process 在捏合反应器中随机放置3000 个粒子,通过粒子示踪技术得到粒子运动轨迹,进而求取拉伸率与混合效率。反应器的拉伸率随混合时间呈指数形式增长,这是有效层流混合的必要条件[36],如图14 所示。随着捏合杆数目的增多,单位时间内捏合次数增加,反应器的拉伸率也随之增大(OPK48-15 mm>OPK36-15 mm>OPK24-15 mm),如图14(a)所示。捏合杆长度对拉伸率的影响如图14(b)所示。可见,拉伸率随着捏合杆长度的增加而增大(OPK24-23 mm>OPK24-15 mm>OPK24-7 mm)。捏合杆长度增加,捏合杆在重叠区域的交互作用增强,粒子在圆周方向上的运动路径也增加。OPK24-disk-15 mm 的桨叶由圆盘和捏合杆组成,OPK24-15 mm 的桨叶仅由捏合杆组成。由于圆盘的存在,粒子的运动轨迹受阻,粒子的运动空间减小,其平均拉伸率会相应减小,因而OPK24-15 mm 的拉伸率大于OPK24-disk-15 mm,如图14(c)所示。 图14 搅拌结构对平均对数拉伸率的影响Fig.14 Influence of kneader configuration on mean length of stretch 重叠区域中的捏合作用对流体进行多次的分裂和折叠,使得流体单元重新定向并继续拉伸,因而时均混合效率的平均值始终保持在零以上,这表明反应器中存在较强的重定向作用[36]。单位时间内捏合次数随着捏合杆数目的增加而增加,流体的重定向作用得到强化,因此时均混合效率随之而增大(OPK48-15 mm>OPK36-15 mm>OPK24-15 mm),如图15(a)所示。随着捏合杆长度的增加,时均混合效率先增加后减小(OPK24-15 mm>OPK24-23 mm>OPK24-7 mm),如图15(b)所示。OPK24-15 mm 的时均混合效率大于OPK24-disk-15 mm,如图15(c)所示。 图15 搅拌结构对时均混合效率的影响Fig.15 Effect of kneader configuration on mean time averaged mixing efficiency (1)反向差速旋转卧式双轴捏合反应器中基本不存在流动死区,桨叶末端区域和重叠区域的流速较大。搅拌单元上的捏合杆数目和搅拌转速呈反比。高流速区域的剪切速率高,高流速和高剪切区域均随着捏合杆数目和捏合杆长度的增加而增大。捏合反应器的自清洁性能也随着捏合杆数目和捏合杆长度的增加而得到增强。 (2)捏合杆可以推动物料在周向上的运动,且在重叠区域存在周期性的捏合作用,进而可以强化径向分布混合过程。随着捏合杆数目增加,单位时间内捏合次数增加,分布混合过程得到强化,因而分离尺度随之减小。捏合杆长度和圆盘对径向分布混合过程和分离尺度的影响较小。 (3)拉伸率随着混合过程的进行呈现指数形式增加,混合效率始终保持大于零,均随着捏合杆数目的增加而增大。拉伸率随着捏合杆长度的增加而增大,时均混合效率随着捏合杆长度的增加呈现先增加而降低的趋势。当桨叶中设置圆盘时,拉伸率和时均混合效率均减小。


2.3 拉伸率与混合效率


3 结 论

