异形喷嘴喷头水滴分布特性试验研究
刘佳玲,万吉祥,李浩,蒋跃
▪灌溉技术与装备▪
异形喷嘴喷头水滴分布特性试验研究
刘佳玲1,2,万吉祥3,李浩1*,蒋跃2
(1.中国农业科学院 农田灌溉研究所/河南省节水农业重点实验室,河南 新乡 453002;2.江苏大学 流体机械工程技术研究中心,江苏 镇江 212013;3.宿迁市水利局,江苏 宿迁 223999)
研究异形喷嘴水滴直径、速度及动能的分布规律。采用视频雨滴谱仪对PY15摇臂式喷头在100、150、200、250、300 kPa共5个工作压力下进行室内无风水滴分布试验。等流量喷嘴的射程:圆形>菱形>椭圆;异形喷嘴的形状系数随出口直径增加而减小,随长径比增加而增大;菱形喷嘴水滴直径沿径向增大的趋势最大。形状系数越大,相同工作压力下的末端水滴直径越小。出口直径越大,射程越远,水滴速度随直径增加的幅度越大。长径比越大,射程越近,水滴平均直径和速度越大。随水滴直径增大,椭圆形喷嘴的水滴速度增幅最小。相同位置处的单位体积水滴打击动能及增长幅度随压力增大而减小。水滴直径和水滴动能沿径向分别呈指数函数和线性函数关系,水滴速度与直径呈对数分布,3个水滴分布预测模型拟合系数都在0.9以上,可以用来模拟异形喷嘴喷头的形状系数、出口直径、长径比与水滴分布特性的关系。
摇臂式喷头;异形喷嘴;视频雨滴谱仪;水滴直径分布;水滴动能分布
0 引言
【研究意义】喷灌是农业节水中一种有效的灌溉方式,喷灌系统一般由水源工程、水泵及动力设备、输水管道系统和喷头等部分组成,其中喷头是实施喷灌的关键设备之一,其性能的优劣不仅直接影响喷洒质量,而且关系到整个喷灌系统的经济性[1-3]。
【研究进展】喷头水力性能主要包括射程、流量、工作压力、喷灌强度、喷灌均匀度、水滴打击强度等。其中,喷灌强度、喷灌均匀度和水滴打击强度都与喷头喷洒水滴分布特性相关。因此,喷头喷洒水滴直径、水滴速度及水滴打击动能是评价喷灌系统质量的重要指标,对喷灌的水力性能有着重要的影响[4-6]。
常规喷嘴喷头的形状为圆形,异形喷嘴作为一种非圆形新型喷嘴,具有改善喷头水量分布、喷洒均匀 性、低压下水力性能比圆形喷嘴更好等优点,在农业喷灌领域得到了广泛的应用。对于各种形状喷嘴的喷头喷洒水滴分布特性,国内外学者做了大量研究。徐红等[7]、SÁNCHEZ等[8]研究了水滴直径分布,得到了喷洒区域的水滴直径正态分布模型、平方根正态分布模型、对数正态分布模型、上限对数正态分布模型(简称ULLN)等。巩兴晖等[9]采用视频雨滴谱仪对NelsonD3000喷头在不同压力下水滴直径沿射程分布进行研究,分析了水滴直径沿射程的变化趋势及水滴速度、角度与水滴直径间的关系,结果表明,水滴直径与射程符合指数函数关系,水滴速度与水滴直径呈对数关系。Lorenzini[10]研究了喷灌喷洒过程中不同工作压力下水滴速度及蒸发的规律,结果表明,空气温度对液滴蒸发有显著影响,在计算液滴蒸发时,空气摩擦可能被错误地忽略。Ouazaa等[11]利用弹道模型研究分析了水滴速度及水滴动能,结果表明,在138 kPa和69 kPa的工作压力下,动能损失随喷嘴直径的增加而减小。朱兴业等[12]通过试验研究了全射流喷头的单个水滴动能、单位体积水滴动能、动能强度分布规律及动能强度均匀性系数与组合间距之间的关系,结果表明,全射流喷头的单个水滴动能分布与水滴直径之间呈幂函数关系,单位体积水滴动能沿径向呈一次函数关系增大。上述研究均针对圆形喷嘴喷头。陈超等[13]研究了菱形、半圆+三角形、半圆+矩形、星形4种形状的异形喷嘴的形状系数对水滴直径的影响,得到了末端水滴直径随形状系数的增大而减小的结论。李栋等[14]讨论了异形喷嘴形状及压力改变对低压射流形态变化的影响,通过试验分析了喷嘴出口形状、压力及入口角改变对射流形态变化的影响。周小引等[15]采用面积相同原则设计了多种异形喷嘴,通过试验讨论了异形喷嘴的喷灌均匀性,发现异形喷嘴的组合均匀性系数显著高于圆形喷嘴的。Jiang等[16]采用高速摄影(HSP)技术研究了异形喷嘴的破碎过程和流动特性,发现三角形射流具有最短的破裂长度和相同压力下射流的扩散角。由于异形喷嘴产生不同的射流形态,异形喷嘴喷头在低压下水力性能得到改善。与圆形喷嘴相比,异形喷嘴的射程降低了,但在低压下的喷灌均匀性更高、水滴分布更均匀。
【切入点】综上可知,异形喷嘴由于其特殊几何结构,具有多变的射流形状,能够降低喷头工作压力,改善喷头的水力性能。对不同喷头工作压力下异形喷嘴水滴分布特性的量化研究将有利于促进异形喷嘴的合理应用。【拟解决的关键问题】以异形喷嘴为研究对象,设计3种不同形状的喷嘴,采用视频雨滴谱仪测试不同工况下不同形状喷嘴的水滴直径分布、水滴速度分布及水滴动能分布规律,探究喷头水力性能对水滴分布特性的影响规律,为进一步提升喷洒性能,选取适宜的异形喷嘴工作压力参数提供理论依据。
1 材料与方法
1.1 异形喷嘴结构设计
异形喷嘴出口截面的尺寸设计可以根据以下2种方法确定:①面积相同原则,即喷嘴出口截面面积相同。以圆形喷嘴的出口截面面积为标准,确保异形喷嘴的出口截面积和圆形喷嘴的出口截面积相等。②流量相同原则,即流过喷嘴的流量相同。以圆形喷嘴的出口面积为标准,通过公式P3 600(g)1/2换算确定对应的异形喷嘴的面积,保证在同一工作压力下异形喷嘴的流量和圆形喷嘴一致。
以常见的圆形喷嘴为对照,采用流量相同原则,设计了椭圆和菱形2种形状的等流量异形喷嘴。圆形喷嘴结构如图1所示。其中,0为圆形喷嘴的出口直径,分别取4、5 mm和6 mm;为喷嘴进口锥角,选取45°;其余结构参数均相同。本文试验研究的9个喷嘴的出口形状和尺寸如表1所示。

图1 喷嘴结构示意(单位:mm)
采用线切割加工法加工出的各喷嘴材质为铝。考虑到误差,在加工完成后进行流量误差试验,发现相同进口锥角和出口直径的异形喷嘴在等压下的流量误差均小于4%(表2),故认为符合流量相同原则。
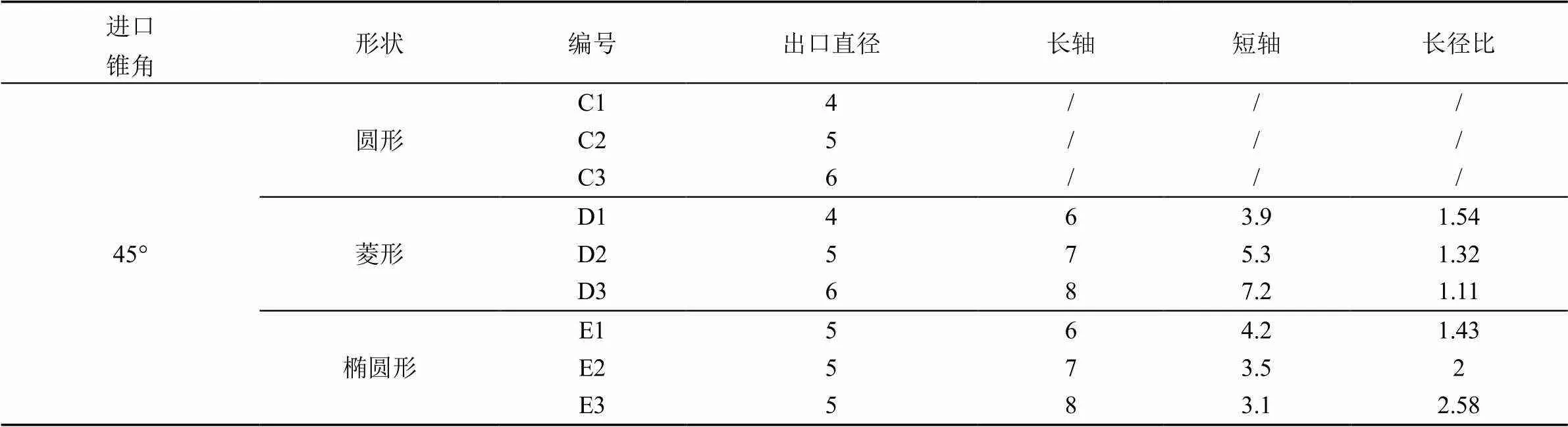
表1 异形喷嘴几何结构参数

图2 喷嘴实物
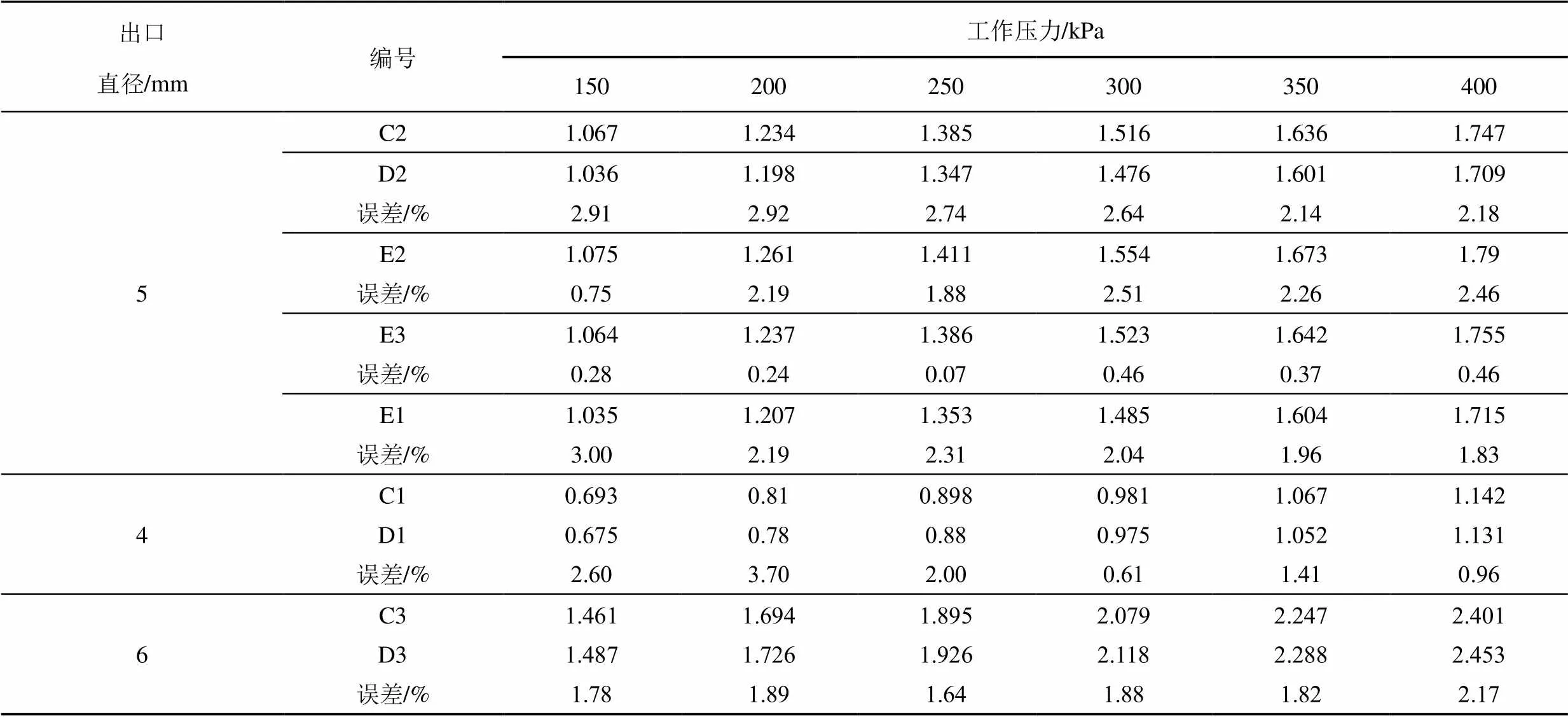
表2 不同压力下等流量喷嘴流量误差
1.2 试验方法
PY15摇臂式喷头水量分布及水滴动能分布试验在直径为44 m的室内无风喷灌实验大厅进行。喷头安装高度为1.4 m,工作压力分别设置为100、150、200、250 kPa和300 kPa。由于喷灌大厅内无风,因此可以用一条射线上的数据代替圆周内的各条射线。将视频雨滴谱仪(由欧洲太空局与欧洲空间技术中心(European Space Agency/European Space and Technology Centre)等机构研制,购买厂家为易科泰生态技术有限公司)在喷头稳定运转10 min后以2 m间距移动,依次测得各点上的水滴直径和水滴速度,雨滴谱仪在每点处的测试时长为喷头旋转经过雨滴谱仪3次。试验系统布置和现场照片见图3、图4。

图3 试验系统布置示意

图4 试验现场
1.3 数据处理方法
1.3.1 形状系数
水滴直径随着距喷头距离的增大而增大,在射程末端达到最大值[7]。因此,末端水滴直径可作为衡量喷头雾化状况的重要依据。
喷嘴形状对水滴直径的影响一般采用形状系数来表示,喷嘴形状越偏离圆形,形状系数越大,喷嘴形状对水滴直径影响越大。的关系式为:

式中:为喷嘴过水断面周长(mm);为喷嘴过水断面面积(mm2)。
1.3.2 水重加权水滴平均直径
国内外常用的计算水滴直径的方法有个数加权法、水重加权平均法和中数直径法[18]。本文计算每个测点处的水滴平均直径采用水重加权平均法。采用Origin进行Exp2PMod1指数拟合,方程式为:
d=ae, (2)
式中:、为拟合系数;为水滴直径;为距喷头初始位置距离。
1.3.3 水滴直径与速度分布规律
喷洒水滴速度是决定水滴打击动能重要因素,通过视频雨滴谱仪测出不同喷嘴不同直径水滴的速度。
水滴直径与速度间存在对数函数关系,关系式为:
ln()[18], (3)
其中:、、为拟合系数;为水滴速度;为水滴直径。
1.3.4 单位体积水滴打击动能[15]
单位体积水滴动能是指在不同测点处的单个水滴动能总和与总体积的比值,关系式为:

式中:ks为单位体积水滴动能(J/L);为水滴直径级名;为粒子直径级数。
2 结果与分析
2.1 形状系数与末端水滴直径
表3为PY15型喷头异形喷嘴不同压力下的射程。由表3可知,对于等流量喷嘴C2、D2、E1、E2、E3,圆形喷嘴的射程>菱形喷嘴的射程>椭圆形喷嘴的射程。出口直径越大,射程越远;长径比越大,射程越近。

表3 PY15型喷头异形喷嘴不同压力下的射程
表4为低压100、150 kPa和标准压力200 kPa下的末端水滴直径。形状系数随出口直径的增加而减小,随长径比的增加而增大。工作压力越大,末端水滴直径越小。形状系数越大,相同工作压力下的末端水滴直径越小。对于等流量喷嘴C2、D2、E1、E2、E3,在低压100、150 kPa下不同长径比椭圆形喷嘴的末端水滴直径均最小,圆形喷嘴末端水滴直径最大;随着压力增加到200 kPa,菱形喷嘴的末端水滴直径最大,圆形喷嘴的末端水滴直径随压力增加下降速度最快。由表3、表4可知,低压下的等流量喷嘴中,椭圆形喷嘴的射程和末端水滴直径都最小;圆形喷嘴的射程最远,末端水滴直径在低压100 kPa和150 kPa下最大,200 kPa时最小;菱形喷嘴射程适中,末端水滴直径在200 kPa最大。
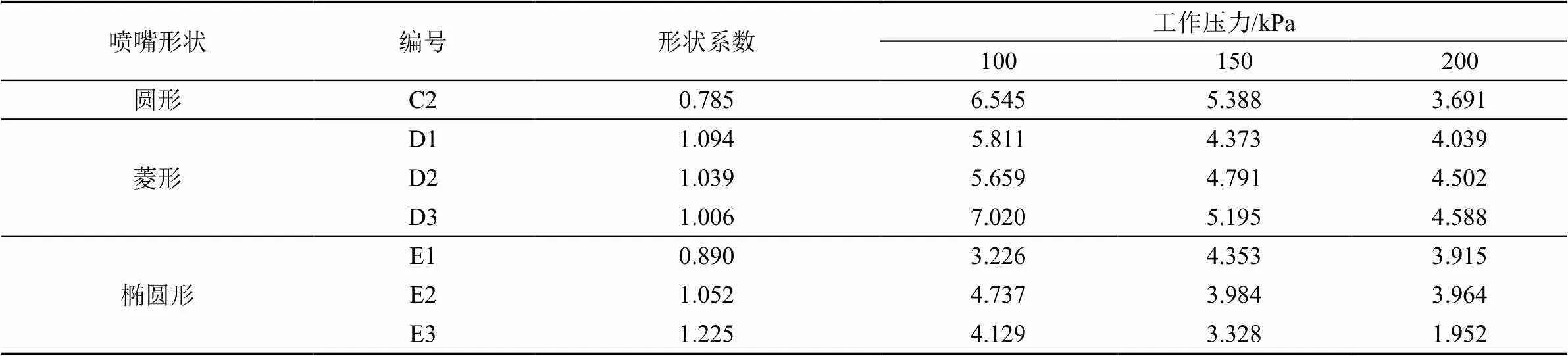
表4 异形喷嘴的形状系数及末端水滴直径
2.2 水滴直径分布
2.2.1 不同压力下水滴直径径向分布
对实测数据进行拟合可以发现,各工作压力下各形状喷嘴的拟合相关系数2都大于0.9,表明该指数函数的拟合精度都较高。
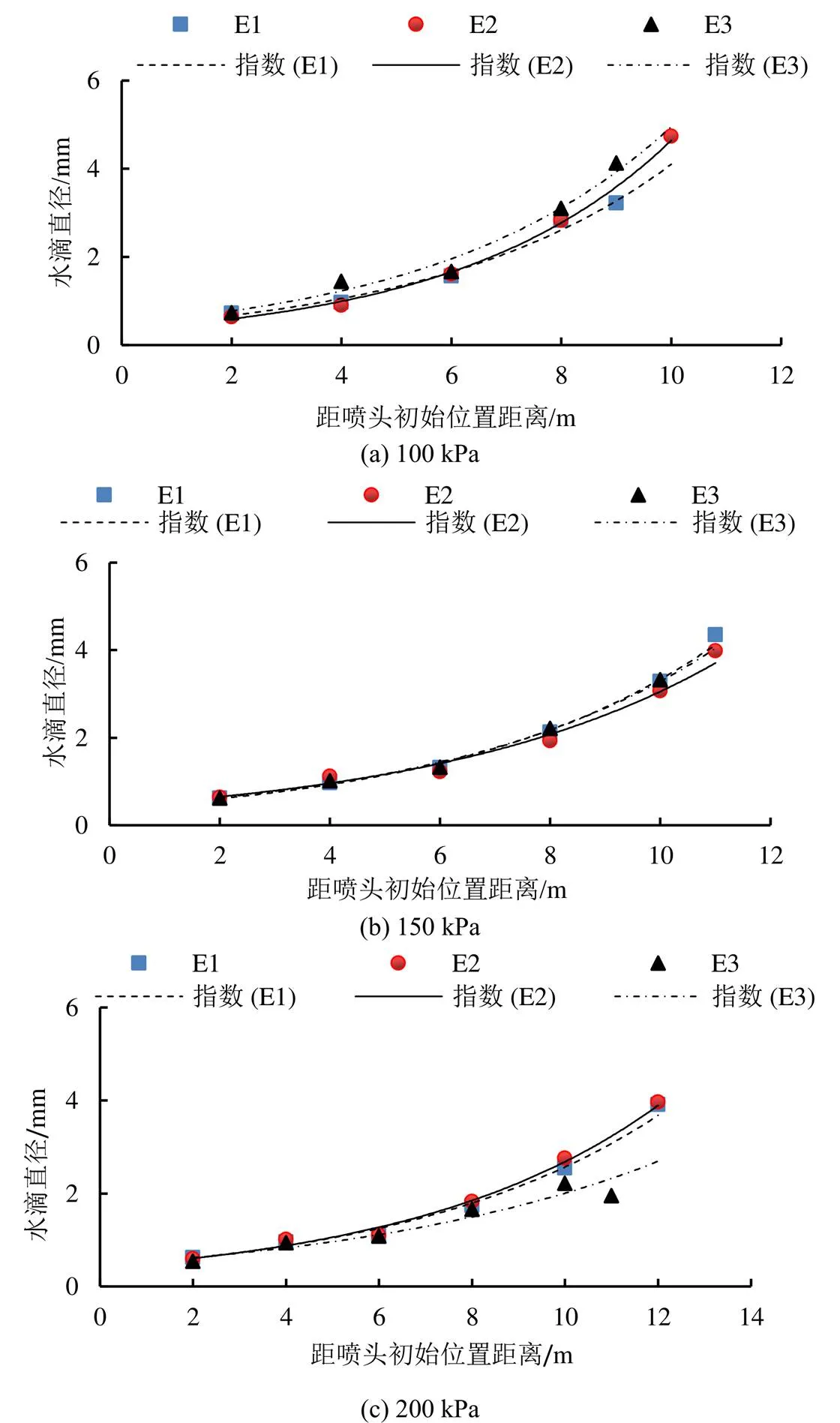
图5为不同工作压力水滴平均直径与距离关系曲线。从图5可以看出,对于同一形状喷嘴,压力越大,指数函数的曲线斜率越小,在相同测点处的水滴平均直径越小,这说明压力增大使得水滴直径沿距喷头初始位置距离增大的趋势减小,射流破碎程度越剧烈。其中圆形喷嘴C2曲线斜率减小的幅度最大。此外,相同压力下,3种形状喷嘴中,菱形喷嘴的曲线斜率最大,圆形最小,这说明菱形喷嘴水滴直径沿距喷头初始位置距离增大的趋势最大。
此外,水滴直径3 mm时,圆形喷嘴C2在100、150、200 kPa下的距喷头初始位置距离分别为7.9、11、12.4 m;菱形喷嘴D2在100、150、200、250 kPa下的距喷头初始位置距离分别为7.6、10、11.7、12.5 m;椭圆形喷嘴E1在100、150、200、250 kPa下的距喷头初始位置距离分别为8.5、9.5、10.7、12.3 m。300 kPa下菱形和椭圆形喷嘴的水滴直径均小于3 mm。由于直径较小的水滴易产生漂移现象和蒸发损失,直径较大的水滴对土壤表面结构的破坏性也较大,不利于水土保持及作物生长,因此适宜喷洒水滴直径范围在1~3 mm范围内,由此可知除100 kPa下椭圆形喷嘴E1的适宜喷洒范围最大,其余工作压力下圆形喷嘴C2的适宜喷洒范围最大。当距离大于8 m后,压力对水滴直径有明显的影响。

2.2.2 不同长径比水滴直径径向分布
对于同一长径比的喷嘴,水滴直径指数函数的斜率随着压力的增加而减小,也就是压力增大使得水滴直径沿径向增大的趋势减小。在相同压力下,同一形状、进口锥角和出口直径的不同长径比的等流量椭圆形喷嘴,距喷头初始位置6 m内,各测点处的水滴直径几乎一致。水滴平均直径沿径向的关系总体满足 E3>E2>E1的规律,即长径比越大,水滴平均直径越大。长径比最大的喷嘴E3射程最短且水滴直径总体最大。长径比最小的喷嘴E1沿径向的水滴直径最小,射程也相对较远。因此,在喷头喷洒中可选取长径比较小的喷嘴。

2.2.3 不同出口直径喷嘴水滴直径径向分布
菱形喷嘴D1、D2、D3进口锥角均为45°,出口直径分别为4、5、6 mm。水滴平均直径及曲线斜率总体上满足D3>D1>D2的关系,即出口直径6 mm>4 mm>5 mm。出口直径最大的喷嘴D3平均水滴直径最大,出口直径5 mm的喷嘴D2平均水滴直径最小,随着压力增加,曲线斜率降低,也就是水滴直径沿纵向增长的幅度下降,且出口直径5 mm的喷嘴D2下降幅度最大。因此,在喷头喷洒中可选取出口直径为5 mm的喷嘴。
2.3 水滴速度分布
2.3.1 不同形状喷嘴水滴速度分布
图8为不同形状喷嘴水滴平均直径与速度关系曲线。由图8可知,相同进口锥角和出口直径的喷嘴,圆形喷嘴速度曲线斜率最大,椭圆形喷嘴斜率最小,也就是随水滴直径的增大,椭圆形喷嘴的水滴速度增长幅度最小。水滴速度随水滴直径的增大而增大,增大的幅度逐渐变小,说明水滴直径是影响水滴速度的重要因素。总的看来,拟合出的3条等流量异形喷嘴的水滴速度与水滴直径的曲线几乎完全一致,说明在流量、进口锥角和出口直径都相同的前提下,喷嘴出口形状对水滴平均直径与速度的关系影响不大。

图8 不同形状喷嘴水滴平均直径与速度关系曲线
2.3.2 不同长径比水滴速度分布
不同长径比的椭圆形喷嘴的水滴直径与速度的关系见图9所示。由图9可知,相同进口锥角、出口直径,不同长径比的椭圆形喷嘴,速度曲线斜率E3>E2>E1,也就是速度曲线的斜率随着长径比的增大而增大,长径比增大使得水滴速度随水滴直径增大的幅度也增大了。相同水滴直径处,喷嘴E2的水滴速度始终最大;在水滴直径小于2.5 mm的范围内,椭圆形喷嘴水滴速度满足E1>E3;水滴直径大于2.5 mm的范围内,水滴速度表现为E3>E1。这说明在最大和最小长径比之间,存在一个中间长径比,在该长径比下,相同水滴直径时的水滴速度最大,水滴打击动能因此也最大。
2.3.3 不同出口直径水滴速度分布
不同出口直径的菱形喷嘴的水滴直径与速度的关系见图10。由图10可知,同一形状及进口锥角的喷嘴,速度曲线斜率表现为D3>D2>D1,也就是曲线斜率随出口直径的增加而增大,出口直径越大,水滴速度随水滴直径增大而增大的幅度越大。在水滴直径小于5 mm的范围内,表现为D1>D2>D3,说明水滴直径相同时,出口直径越大,水滴速度越小。

图9 不同长径比水滴平均直径与速度关系曲线

图10 不同出口直径水滴速度与距离关系曲线
2.4 单位体积水滴打击动能分布规律
图11为不同压力下单位水滴动能的径向分布图。压力越大,相同位置处的单位体积水滴打击动能越小,打击动能的增长幅度越小,对作物、土壤的破坏性越小。在近距离2 m处,各工作压力下各喷嘴的单位体积水滴打击动能相差不大。由图11(a)—图11(c)可知,在各工作压力下相同进口锥角和出口直径的等流量喷嘴中,椭圆形喷嘴的最大单位体积水滴打击动能最小。在100 kPa下,圆形喷嘴的最大单位体积水滴打击动能最大。由图11(c)—图11(e)可知,长径比越大,射程越短。在100 kPa下长径比最小的椭圆形喷嘴E1的最大单位体积水滴打击动能最小;在150~300 kPa下,长径比最大的喷嘴E3的最大单位体积水滴打击动能最小。由图11(b)、图11(f)、图11(g)可知,在100~200 kPa下,出口直径越小,单位体积水滴打击动能越小。
为了进一步研究异形喷嘴喷头的单位体积水滴动能径向分布规律,本文通过对各压力下各喷嘴的单位体积水滴动能进行回归分析,建立水滴动能与距喷头距离分布模型[13]:
ks=, (5)
式中:、为拟合系数;ks为单位体积水滴动能;为距喷头初始位置距离。

异形喷嘴喷头的单位体积水滴动能拟合系数均在0.9以上,拟合精度较高。
将3个不同长径比的椭圆形喷嘴在不同工作压力下的单位体积水滴动能数据进行统一回归,对单位体积动能进一步分析,建立异形喷嘴喷头单位体积水滴动能ks、距喷头距离、长径比与工作压力关系的数学模型,函数关系式为:
ks=2.775-0.318+0.0 926+0.932 (2=0.924),(6)
式中:、为拟合系数;ks为单位体积水滴动能;为距喷头初始位置距离。
不同长径比椭圆形喷嘴的单位体积水滴动能拟合系数在0.924,这说明拟合精度较高。
3 讨论
现有异形喷嘴喷头水滴分布特性的研究,多以形状及压力改变对射流形态变化的影响为重点[13-16],本研究使用视频雨滴谱仪,补充研究了异形喷嘴的形状及压力对水滴直径、速度、动能等水滴分布特性的影响。本研究表明,异形喷嘴的形状系数随出口直径的增加而减小,射程随出口直径的增加而增大。形状系数越大,相同工作压力下的末端水滴直径越小,与陈超等[13]研究异形喷嘴形状系数的试验结论一致。水滴直径沿径向增大的趋势随压力增大而减小。出口直径越大,水滴速度随水滴直径增大而增大的幅度越大。当水滴直径相同时,出口直径越大,水滴速度越小。相同位置处的单位体积水滴打击动能及其增长幅度随压力的增大而减小。与朱兴业等[12]研究全射流喷头喷洒规律结论接近。
除此之外,本文补充研究了异形喷嘴的长径比对喷洒水力性能和水滴分布特性的影响。异形喷嘴的形状系数随长径比的增加而增大,射程随长径比的增加而减小。在5种工作压力下,菱形喷嘴水滴直径沿径向增大的幅度最大。长径比越大,水滴速度随水滴直径增大而增大的幅度越大。随水滴直径的增大,椭圆形喷嘴的水滴速度增长幅度最小,圆形喷嘴增幅最大。出口直径5 mm的喷嘴平均水滴直径最小,且水滴直径沿纵向增长的下降幅度最大。
4 结论
1)采用视频雨滴谱仪测量技术对异形喷嘴喷头水滴直径、速度及动能分布进行试验,并建立能准确反映异形喷嘴喷头水滴直径、水滴速度、单位体积水滴动能分布规律的预测模型,5种工作压力下7个异形喷嘴的模型拟合相关系数都在0.9以上。喷嘴的长径比越大,最大单位体积水滴打击动能就越小。各工作压力下的等流量喷嘴中,椭圆形喷嘴的最大单位体积水滴打击动能最小。
2)在100、150、200、250、300 kPa工作压力下,异形喷嘴喷头的长径比越大,水滴平均直径越大。在相同工作压力下,不同长径比的等流量椭圆形喷嘴,在距喷头初始位置6 m内,各测点处的水滴直径几乎一致。
[1] 鲍亚, 刘俊萍, 刘兴发, 等. 压力对低压喷头水量分布模型影响的试验研究[J]. 排灌机械工程学报, 2016, 34(1): 81-85.
BAO Ya, LIU Junping, LIU Xingfa, et al. Experimental study on effects of pressure on water distribution model of low-pressure sprinkler[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34(1): 81-85.
[2] 李佳, 徐峥嵘. 设施园艺发展节水灌溉研究:评《节水灌溉技术》[J]. 灌溉排水学报, 2020, 39(1): 146.
[3] 朱兴业, 史永杰, 胡广, 等. 射流式喷头水量分布动态仿真及试验[J]. 灌溉排水学报, 2020, 39(4): 74-83.
ZHU Xingye, SHI Yongjie, HU Guang, et al. Dynamic simulation and test of water distribution of fluidic sprinkler[J]. Journal of Irrigation and Drainage, 2020, 39(4): 74-83.
[4] 袁寿其, 李红, 王新坤. 中国节水灌溉装备发展现状、问题、趋势与建议[J]. 排灌机械工程学报, 2015, 33(1): 78-92.
YUAN Shouqi, LI Hong, WANG Xinkun. Status, problems, trends and suggestions for water-saving irrigation equipment in China[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(1): 78-92.
[5] 吴普特, 朱德兰, 吕宏兴. 灌溉水力学引论[M]. 北京: 科学出版社, 2012.
[6] 涂琴, 李红, 王新坤, 等. 基于灰色关联法的多喷头轻小型喷灌机组比选[J]. 江苏大学学报(自然科学版), 2014, 35(6): 656-662.
TU Qin, LI Hong, WANG Xinkun, et al. Comparison and selection of small-scale irrigation machines with multiple sprinklers based on grey relational analysis[J]. Journal of Jiangsu University (Natural Science Edition), 2014, 35(6): 656-662.
[7] 徐红, 龚时宏, 贾瑞卿, 等. 新型ZY系列摇臂旋转式喷头水滴直径分布规律的试验研究[J]. 水利学报, 2010, 41(12): 1 416-1 422.
XU Hong, GONG Shihong, JIA Ruiqing, et al. Study on droplet size distribution of ZY sprinkler head[J]. Journal of Hydraulic Engineering, 2010, 41(12): 1 416-1 422.
[8] SÁNCHEZ BURILLO G, DELIRHASANNIA R, PLAYÁN E, et al. Initial drop velocity in a fixed spray plate sprinkler[J]. Journal of Irrigation and Drainage Engineering, 2013, 139(7): 521-531.
[9] 巩兴晖, 朱德兰, 张林, 等. 基于2DVD的非旋转折射式喷头水滴直径分布规律[J]. 农业机械学报, 2014, 45(8): 128-133, 148.
GONG Xinghui, ZHU Delan, ZHANG Lin, et al. Drop size distribution of fixed spray-plate sprinklers with two-dimensional video disdrometer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(8): 128-133, 148.
[10] LORENZINI G. Water droplet dynamics and evaporation in an irrigation spray[J]. Transactions of the ASABE, 2006, 49(2): 545-549.
[11] OUAZAA S, BURGUETE J, PANIAGUA M P, et al. Simulating water distribution patterns for fixed spray plate sprinkler using the ballistic theory[J]. Spanish Journal of Agricultural Research, 2014, 12(3): 850.
[12] 朱兴业, 刘兴发, 刘俊萍, 等. 全射流喷头喷洒水滴动能分布规律[J]. 农业工程学报, 2015, 31(15): 26-31.
ZHU Xingye, LIU Xingfa, LIU Junping, et al. Droplet kinetic energy distribution regulation of complete fluidic sprinkler[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(15): 26-31.
[13] 陈超, 袁寿其, 李红, 等. 异形喷嘴对变量喷头水力性能的影响[J]. 农业机械学报, 2011, 42(12): 111-115.
CHEN Chao, YUAN Shouqi, LI Hong, et al. Effect of non-circle nozzle on hydraulic performance of impact variable-rate sprinkler[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(12): 111-115.
[14] 李栋, 卢晓江, 赵欣. 异形喷嘴低压射流形态的实验研究[J]. 轻工机械, 2006, 24(3): 18-20.
LI Dong, LU Xiaojiang, ZHAO Xin. Experimental study on low pressure jet characteristic of the non-circle jet nozzle[J]. Light Industry Machinery, 2006, 24(3): 18-20.
[15] 周小引, 李红, 蒋跃. 低压喷头异形喷嘴水量分布均匀性试验研究[J]. 排灌机械工程学报, 2017, 35(5): 448-453.
ZHOU Xiaoyin, LI Hong, JIANG Yue. Study on water distribution uniformity of non-circular nozzles at low pressure[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(5): 448-453.
[16] JIANG Y, LI H, HUA L, et al. Experimental study on jet breakup morphologies and jet characteristic parameters of non-circular nozzles under low-intermediate pressures[J]. Applied Engineering in Agriculture, 2019, 35(4): 617-632.
[17] 朱兴业, 刘兴发, 刘俊萍, 等. 基于LPM的摇臂式喷头水滴分布试验研究[J]. 排灌机械工程学报, 2015, 33(10): 908-914.
ZHU Xingye, LIU Xingfa, LIU Junping, et al. Droplets distribution research of impact sprinkler based on Laser Precipitation Monitor[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(10): 908-914.
[18] 吴普特, 朱德兰, 吕宏兴, 等. 农田灌溉过程中的水力学问题[J]. 排灌机械工程学报, 2012, 30(6): 726-732.
WU Pute, ZHU Delan, LYU Hongxing, et al. Hydraulics problems in farmland irrigation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(6): 726-732.
Distribution of Water Droplets of Non-circular Sprinkler Nozzles
LIU Jialing1,2, WAN Jixiang3, LI Hao1*, JIANG Yue2
(1. Chinese Academy of Agricultural Sciences, Farmland Irrigation Research Institute/Henan Province Water-saving Agriculture Key Laboratory, Xinxiang 453002, China; 2. Jiangsu University the Research Center for Fluid Mechanical Engineering Technology, Zhenjiang 212013, China; 3. Suqian Water Resources Bureau, Suqian 223999, China)
【】The distribution of water droplet diameter of the sprinkler nozzle is an important parameter in designing sprinkler irrigation. The purpose of this paper is to study how non-circular nozzles affect this distribution.【】We studied two non-circular nozzles: an rhombic nozzle and an elliptical nozzle. By keeping the spraying rate the same, we compared the distribution of water droplet diameters of each nozzle using the PY15 rocker arm by keeping the working water pressures in the range of 100 to 300 kPa. For each test, we measured the distribution of the droplet diameters using a video raindrop spectrometer, with that measured from round circular nozzle taken as the control.【】The diameter of coverage of all nozzles was ranked in the order of round > rhombic > elliptical. Shape coefficient of the non-circular nozzle decreased as the outlet diameter of the nozzle increased while increased as the length-diameter ratio increased. The diameters of water droplets of the rhombus nozzle increased most quickly in the radial direction, compared to the other two nozzles. When working water pressure was the same, the diameter of the end-water droplet decreased as the shape coefficient of the nozzle increased; the diameter of the coverage increased with the diameter of the nozzle outlet. Increasing the outlet diameter can speed up the droplet velocity, while increasing the diameter-length ratio reduces the maximum distance that the droplets can reach due to the increased droplet diameter and velocity. The increase in droplet velocity of the elliptical nozzle with droplet diameters was the least. The kinetic energy and the increase in amplitude of unit volume of the droplets at the same location both decreased as the working water pressure increased. The diameter and kinetic energy of the droplets increased with the radial distance exponentially and linearly, respectively, while the relationship between velocity and diameter of the droplets was logarithmic.【】Geometrical shape of the sprinkler nozzle has a significant impact on the diameters of the water droplets and their spatial distributions.
Non-circular nozzle; water droplet diameter; kinetic energy; spatial distribution
刘佳玲, 万吉祥, 李浩, 等. 异形喷嘴喷头水滴分布特性试验研究[J]. 灌溉排水学报, 2021, 40(12): 85-92, 118.
LIU Jialing, WAN Jixiang, LI Hao, et al. Distribution of Water Droplets of Non-circular Sprinkler Nozzles[J]. Journal of Irrigation and Drainage, 2021, 40(12): 85-92, 118.
S277.9
A
10.13522/j.cnki.ggps.2021143
1672 - 3317(2021)12 - 0085 - 09
2021-04-12
国家自然科学基金项目(51809119);河南省节水农业重点实验室开放课题(FIRI202001-0101)
刘佳玲(1997-),女。硕士研究生,主要从事异形喷嘴喷灌优化与节水灌溉。E-mail: 17805015863@qq.com
李浩(1987-),男。副研究员,博士,主要从事节水灌溉技术与设备方面的研究。E-mail: lihao01@caas.cn
责任编辑:白芳芳

