地震作用下边坡台阶对均质公路路堑边坡的动力响应影响研究
李 波,方俊杰,冯志国
(国家林业和草原局昆明勘察设计院 昆明市 650216)
0 引言
我国是一个疆域辽阔、地质环境十分复杂的国家,特别是西南部地区,该区域多为山地、高原,地质作用强烈,山势陡峻、沟壑丛生,使得该区域的基础设施建设尤为困难。我国地质灾害种类繁多,对公路工程的建设危害也巨大。涉及山区公路工程安全的主要有边坡坍塌、崩塌、滑坡、泥石流等,其中公路路堑边坡的稳定性导致的灾害和次生灾害已经成为主要地质灾害之一。由于我国受太平洋板块、印度板块和菲律宾海板块的挤压,地震断裂带十分发育,特别是西部西南部地区,地震活动频发。随着我国近年来对西部地区投资的加大,大量公路工程将建设在西南部地震区,地震作用下公路工程的稳定性要求显得越来越重要。由于西南部特殊的地形条件,公路建设不可避免地会造就大量的路堑边坡,因此地震作用下的公路路堑边坡的稳定问题已经成为公路工程稳定性研究中的重点和难点问题[1-2]。
目前地震荷载作用下公路路堑边坡的动力响应分析方法主要:大型振动台模型试验分析法、滑块分析法、拟静力法、有限单元法、有限差分法、动力时程分析法[3]等,这些方法都有各自运用领域和优缺点。公路路堑边坡地震作用下的动力响应包括加速度、位移、速度、应力响应等。探讨各参数响应规律对地震荷载下边坡的稳定性分析和抗震治理有着极为重要的意义,这些不同参数的变化也直接或间接地反应了边坡在地震作用下的变化规律。
以西南地区某二级公路均质路堑边坡为例,对该边坡分不同台阶并建立相应的边坡模型,输入水平和竖直耦合的实测地震波,并对该路堑边坡在实测地震波作用的动力响应谱规律进行研究。总结加速度、速度、位移、应力等时程曲线的响应规律,为公路路堑边坡的抗震设计提供理论依据。
1 路堑边坡动力模型及参数选取
1.1 边坡模型简化
该公路路堑边坡位于澜沧江沿江二级公路K90+080~K90+300段右侧,右侧原为耕地,路线从耕地下方挖方经过,设计坡比为1∶1。据详勘报告,0~2m的耕植土、素填土,2~30m均为粉质黏土,土体重度为19.6kN/m3,弹性模量为8.6MPa,泊松比为0.365,黏聚力为31.5kPa,内摩擦角为17.2°。段落长度约220m,目前总体稳定,段内边坡最高处为20m左右,最低处为16m左右,全段平均坡高约18m左右。由于该段边坡沿路线方向较长、土质均匀,为简化模型,提高软件计算效率,可以将这样纵向很长且土质材料均匀的路堑边坡的三维变形简化为二位平面变形问题。简化后的计算模型坡比为1∶1,坡高取平均坡高约18m。根据《中国地震动峰值加速度区划图》(GB 18306—2015),该段路线所经区域的设计基本地震加速度值为 0.20g,根据《中国地震动反应谱特征周期区划图》(GB 18306—2015),该段路线所经区域的反应谱特征周期为 0.4s,抗震设防烈度为8度[4]。
为探寻边坡台阶对该路堑边坡的动力响应规律,在边坡高度、设计坡比不变的情况下,分别模拟设置了一个台阶的二级边坡和两个台阶的三级边坡,并与不设置台阶的单级边坡进行对比,希望由此探索边坡设立台阶后的动力响应规律和动力破坏模式,为多台阶边坡地震作用下锚固提供理论依据[5]。
采用有限元软件ANSYS对以上三种情况建立二维分析计算模型,对模型划分有限单元网格,如图1~图3所示,并在边坡坡面和坡体内部设置相应的监测点。
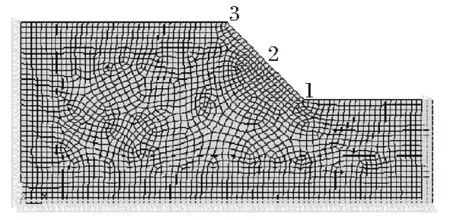
图1 一级边坡网格模型及监测点
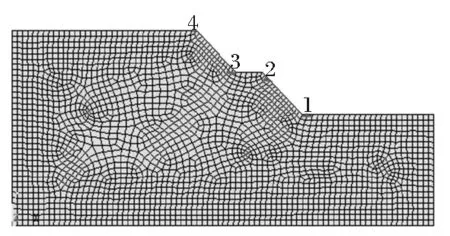
图2 二级边坡网格模型及监测点
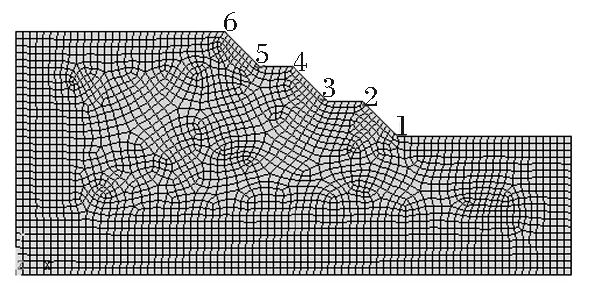
图3 三级边坡网格模型及监测点
1.2 边界条件
路堑边坡底部施加竖直和水平两个方向的约束,坡前和坡后施加竖直的单向约束,边坡坡顶和边坡临空面竖直和水平两个方向均不施加约束,用于模拟坡面和坡顶土体的变形和破坏。
1.3 地震荷载的选取和输入方式
选择世界上第一条成功记录全过程的地震波—1940年5月18日位于加州南部的EI-Centro地震波,该地震波完整记录时间为54s,计算截取前段最具代表性的20s,如图4。输入地震波时,采用竖直和水平的双向耦合输入,分别探讨输入地震波后不同台阶数均质公路路堑边坡的坡面方向动力响应参数的变化规律。
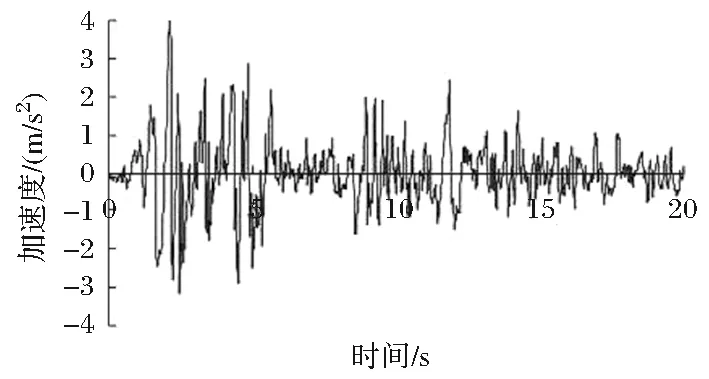
图4 EI波水平加速度时程曲线
2 EI-Centro地震波作用下路堑边坡的动力响应规律
2.1 均质公路路堑边坡坡面各监测点的动力响应规律
为研究路堑边坡在耦合输入地震波时坡面方向的动力响应规律,分别在不同台阶数边坡的坡面设置不同监测点,如图1~图3,研究其加速度、速度、位移的变化,总结其动力响应规律,由此为地震作用下多台阶边坡的治理提供理论依据。限于文章篇幅未列出监测点的参数时程曲线,仅将时程曲线上各分量最大值和最小值统计于表1~表3。
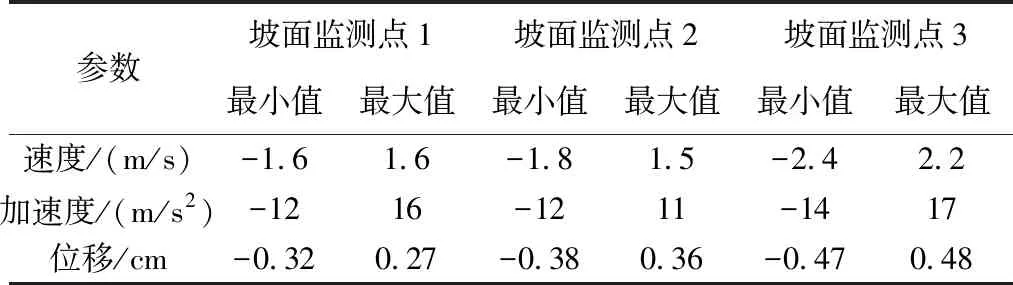
表1 无台阶边坡不同监测点的最值统计表

表2 一台阶边坡不同监测点的最值统计表
根据该公路路堑边坡坡面各监测点的速度、加速度、位移时程曲线,统计各曲线的极值,如表1~表3,分析对比数据,可得出以下结论:

表3 二台阶边坡不同监测点的最值统计表
(1)对于无台阶的一级边坡
边坡水平位移、速度、加速度分布大致呈现沿坡面向上逐渐增大的趋势,坡脚位置最小、坡中次之、坡顶点处最大,说明边坡对所输入的地震波有沿坡面向上放大的趋势,称之为边坡地震作用下的临空面放大效应。
(2)对于一台阶的二级边坡
①坡面上各突出点的位移、速度、加速度相对于坡脚点都有所增大,区别在于,各参数极值点不是出现在坡顶点,而是出现在第一级边坡顶2点处,这说明一台阶边坡最易破坏点为第一级边坡的顶点,在治理时应该重点治理第一级,所对应的锚杆锚索长度也应较长。
②第二级边坡坡脚3点有相反的趋势,此点的速度、加速度最小,说明振动反应最轻微,此点为边坡的安全点。
③计算边坡三量最大值和坡脚点的比值,也就是边坡各参数的放大系数,并与无台阶一级边坡进行对比。位移放大系数由1.816降到1.427,速度放大系数由1.295降到1.210,加速度放大系数由1.251降到1.231,由此证明分台阶处理后对控制边坡位移、速度和加速度是有利的。
(3)对于二台阶的三级边坡
①二台阶三级边坡每一级的顶点,即2、4、6点相对于坡脚点1,速度、加速度、位移三量都有放大趋势,但和一台阶边坡有所不同,最大的位移、速度、加速度均出现在坡顶点6,其次是2点,增量最小的是4点,说明第三级最危险,其次是第一级、第二级。锚固设计时可由此确定主次关系,并相对应的优化锚杆锚索设计长度,提高治理的效率和经济性。
②后缘点3和点5相对于坡脚点1,位移有增大趋势,但增大幅度较小,速度和加速度减弱,这是由此处应力集中导致的,滑动体可能由此出露。
③将无台阶边坡、一台阶边坡和二台阶边坡的各参数放大系数[6]进行比较可以发现,位移放大系数分别为1.816、1.427和1.285,速度放大系数分别为1.295、1.210和1.201,加速度放大系数分别为1.251、1.231和1.212。随着台阶数的增加,放大系数呈现逐步减小的趋势,由此可见增加台阶可以使边坡受力更加均匀,有利于控制边坡的位移。因此分台阶处理边坡可以降低边坡的地震动力反应,提高边坡动力稳定性。
2.2 均质公路路堑边坡的应力分布动力响应规律
为了更形象地观察耦合输入EI地震波后边坡内部应力的变化,给出了边坡最后一个计算子步的水平向应力云图和平均应力云图,如图5、图6,通过应力云图可以很好地验证上述结论。

图5 水平应力云图
通过分析边坡的各计算子步的水平向应力云图和平均应力云图的变化规律,可得出如下结论:
(1)对于应力的分布,各台阶边坡均发生了应力集中的现象,差别在于集中的位置和程度不一。无台阶的一级边坡应力首先集中在坡顶和坡脚以下,主要沿着坡体内部一倍坡高处集中,大体呈圆弧形趋势发展,这表明随着地震荷载的输入,边坡有可能沿着此应力带破坏,最终从负应力较为集中的坡脚出露。
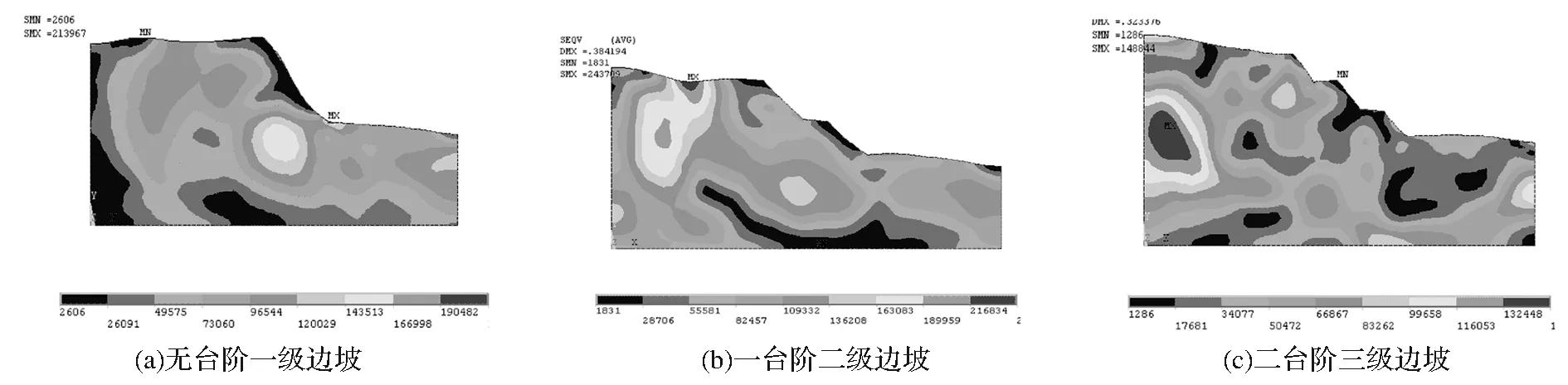
图6 平均应力云图
(2)对于一台阶的二级边坡:应力分布动力响应规律在坡体内部大致与无台阶边坡相同,应力均首先集中在坡顶和坡脚以下一倍坡高处,并由此沿坡体内部呈圆弧形发展。应力集中区别在于坡面处,其中1、2、4点应力集中明显,为坡面危险点。3点应力较小,为安全点。一级边坡坡面应力整体大于二级边坡坡面应力,边坡锚固设计时,应重点治理一级边坡,二级次之。
(3)对于二台阶的三级边坡:由于设置了两个台阶,在地震荷载作用下受力最为均匀,在输入地震波以后没有出现明显的塑性带,坡脚以下一倍坡高处应力最为集中,坡体内部塑性集中不明显,呈现多点分布的趋势。坡面应力分布也有不同,随着地震动荷载的增加,三级边坡坡顶处6点首先出现应力集中,其次是一级边坡坡顶处2点,最后是二级边坡坡顶处4点。由此进一步证明二台阶三级边坡在地震作用下的最危险位置依次为第三级、第一级和第二级坡,与2.1节结论一致,边坡锚固设计可由此确定主次关系并由此调整锚杆锚索设计长度。
3 结论
通过对竖直和水平双向耦合输入地震波时三种不同边坡模型各位置监测点的各参数时程曲线和应力分布的分析,可得出以下结论:
(1)对于一台阶的二级边坡:最易破坏点为第一级边坡的顶点,治理时应该重点治理第一级,第一级的锚杆锚索长度也应较长。应力分布规律在坡体内部大致与无台阶边坡相同,首先集中在坡顶和坡脚以下一倍坡高处,并由此沿坡体内部呈圆弧形发展。
(2)对于二台阶的三级边坡:坡面应力分布随着地震动荷载的增加,顶处6点首先出现应力集中,其次是2点,最后是4点。因此第三级最危险,其次是第一级、第二级。输入地震波以后没有出现明显的塑性带,坡体内部塑性集中不明显,呈现多点分布的趋势。二台阶边坡的锚固设计时可由此确定主次关系,并由此优化锚杆锚索的设计长度,提高治理的效率和经济性。
(3)将无台阶边坡、一台阶边坡和二台阶边坡的各参数放大系数进行比较可以发现,位移放大系数分别为1.816、1.427和1.285,速度放大系数分别为1.295、1.210和1.201,加速度放大系数分别为1.251、1.231和1.212。随着台阶数的增加,放大系数呈现逐步减小的趋势,由此可见增加台阶可以使边坡受力更加均匀,有利于控制边坡的位移。因此分台阶处理边坡可以降低边坡的地震动力反应,提高边坡动力稳定性。

