自动旋转式喷涂机喷涂轨迹优化

李三平，杜佳宝，杨春梅，任长清，张庆明，侯玉宁

自动旋转式喷涂机喷涂轨迹优化

李三平，杜佳宝，杨春梅，任长清，张庆明，侯玉宁

（东北林业大学，哈尔滨 150040）

实现包装生产线上的自动化高效涂装作业，建立待喷涂工件表面的漆膜厚度分布模型，优化喷涂轨迹，求解最佳的喷涂工件的进给速度和自动旋转式喷涂机的旋转速度，实现自动旋转式喷涂机的喷涂轨迹优化。通过自动旋转式喷涂机进行喷涂试验，获得漆膜厚度数据，通过分布模型表征试验数据，运用Matlab遗传算法工具箱拟合出分布模型的关键参数。根据自动旋转式喷涂机喷涂过程，确定喷涂轨迹方程，在此基础上建立漆膜厚度搭接模型，通过NSGA-Ⅱ算法求解出最佳的进给速度和喷涂机的旋转速度。根据NSGA-Ⅱ算法进行优化得出被喷涂工件的进给速度为428.849 mm/s，喷涂机的旋转速度为6.22 rad/s，工件的喷涂时间为6.995 s。被喷涂表面的漆膜厚度模型能够准确地反映被喷涂工件表面的实际喷涂情况，能够对自动旋转式喷涂机的喷涂轨迹进行合理优化，为实现包装领域内的自动化涂装作业奠定了基础。

漆膜厚度分布；分布模型；遗传算法；NSGA-Ⅱ算法

目前，喷涂机器人已广泛应用于包装行业，其作为一种包装机械是离线编程技术与机械技术相结合的自动化喷涂设备，可在包装、皮具、汽车外壳修饰、家具产业等领域广泛使用。我国木工包装机械起步较晚，但发展极为迅速，传统的人工喷涂方式被自动包装机械所取代。截至2016年我国木门产量超11 300万套，产值超过1400亿元，产量和产值均居世界第1位，成为名副其实的木工机械生产大国[1]。这也给我国木制产品喷涂的包装机械带来了更大的挑战，因此，我国喷涂的包装机械应该朝着智能化、自动化方向全面发展[2]。为此文中提出一种高效的自动旋转式喷涂机，并对其喷涂轨迹进行优化，对漆膜厚度均匀性进行研究。

在包装领域内，涂装作业是包装喷涂生产中关键的程序，它不仅能够保证被喷涂工件表面的防护性能还极大地提高了被喷涂工件的美感。目前，机器人喷涂在包装工业生产的流水线上已经广泛应用，离线编程技术也成为包装喷涂产业最常用的编程方式[3]。离线编程技术能够对机器人的喷涂轨迹进行优化使包装中的喷涂表面漆膜厚度均匀性更好，因此，机器人喷涂的离线编程技术成为了研究热点[4]。近年来，国内外学者对喷涂机器人的离线编程技术进行了许多研究，且取得了一定成果。Zhou等[5]利用微分几何原理建立了倾角喷雾模型。提出了3种情况下的圆柱表面倾角喷涂路径优化模型，并对其进行了比较，确定了获得最佳喷涂质量的最佳方案。Li C等[6]通过定点喷涂实验，检测膜厚，建立喷枪的三维模型，分别对膜厚和曲面累积率进行建模。对漆膜厚度均匀性进行优化，找到喷枪的最佳速度和最佳喷枪间距，实现了喷枪轨迹的优化。Guan L等[7]提出了一种新的轨迹生成方法，以优化相邻交界处的过渡段，根据patch法向量的不同角度，实现直线、凸弧和凹弧组合。马淑梅等[8]利用B样条技术拟合曲面，对船舶工业机器人曲面喷涂轨迹进行了合理规划。陈雁等[9]利用欧拉拉格朗日法建立球形面漆膜模型，对球形面成膜特性进行了研究。Teng K等[10]在现有的将复杂曲面划分成满足约束的小块的方法的基础上，提出了2种路径模式的路径优化算法。通过修改喷枪路径的规划方向，提出了2种算法对螺旋路径和锯齿路径进行优化。Giulio T等[11]提出了一种工业机器人喷涂轨迹规划的新方法。该方法以操作空间中末端执行器路径的任意参数描述作为输入，提供可行的运动轮廓。此外，朱由锋等[12]对喷涂机的悬臂梁进行参数振动分析，研究了振动特性对喷涂机喷涂效率和稳定性的影响。

目前针对自动旋转式喷涂机喷涂轨迹优化的研究较少，文中主要通过对被喷涂工件表面的漆膜厚度数据，采用遗传算法拟合出其表面的漆膜厚度分布模型，并运用NSGA-Ⅱ算法对工件的进给速度和自动旋转式喷涂机的旋转速度进行了优化，实现对自动旋转式喷涂机的轨迹优化，最后通过Matlab软件进行漆膜厚度仿真，验证方法的有效性。

1 喷涂试验设计

为了获得各点的喷涂厚度，文中采用了自动旋转式喷涂机（以下简称喷涂机）进行喷涂试验。该机配置了旋转的喷枪架，旋转的喷枪架安装6支喷枪，6支喷枪协同工作极大地提高了包装产业中的喷涂作业效率。其结构见图1。此次试验以木门为喷涂对象，木门的长度=2000 mm，宽度=800 mm。喷枪与被喷涂工件的距离=200 mm，木门以恒定的速度向前进给。喷涂过程中采取单支喷枪喷涂轨迹进行喷涂试验。当木门完全离开喷枪范围后，喷涂完毕，关闭自动旋转式喷涂机。试验喷涂后木门表面的喷涂情况见图2。待漆膜完全干燥后，取木门中心建立坐标轴。采用DeFelsko PosiTector 200系列超声波涂层测厚仪（美国狄夫斯高公司）。对漆膜厚度进行测量，每点测量3次取平均值作为漆膜厚度。测点位置（在垂直轴的位置上均匀地选取截面）见图3。喷涂过程中木门做匀速直线运动，自动旋转式喷涂机以恒定的速度转动，在垂直于轴方向上的不同断面上漆膜厚度分布基本一致。为消除试验测量时产生的误差，在多个断面上对漆膜的厚度进行测量，以同一值下的测量数据取平均数作为测量数据，见表1（列出部分数据）。

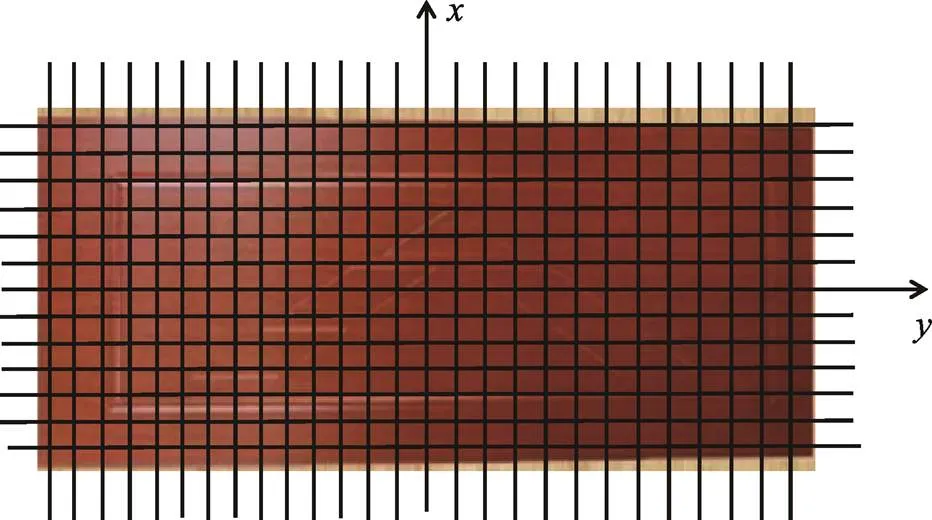
图3 木门表面漆膜测点位置

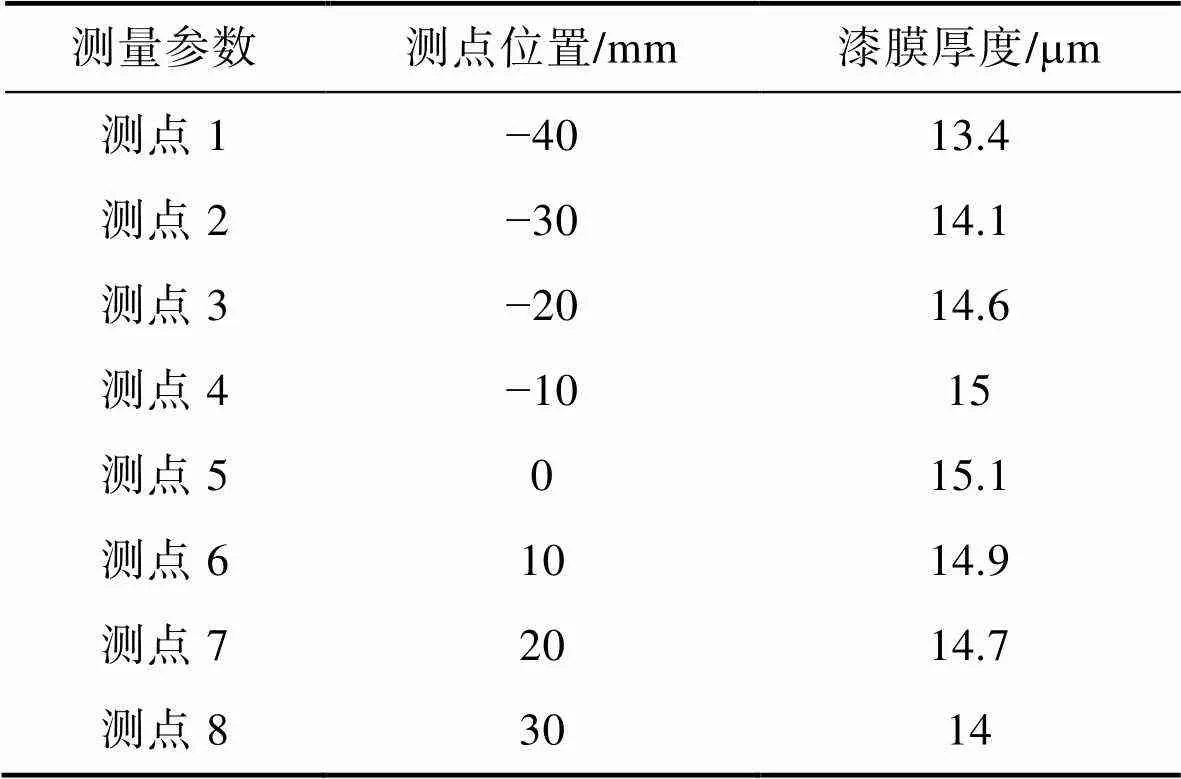
表1 单支旋转喷枪喷涂后漆膜厚度测量数据

2 喷枪轨迹模型的建立

2.1 β分布模型的建立

目前有许多的漆膜厚度生长模型，如无限范围模型里的高斯分布模型[13]和柯西分布模型[14]、有限范围模型[15]和分布模型[16]等。对于平面喷涂来说，分布模型的涂层厚度变化量比其他分布模型的变化量小，因此文中选取分布模型作为漆膜厚度速率累积模型的基础。

分布模型可以抽象为分布函数。假设喷枪在喷涂过程中的喷幅区域为椭圆形，设椭圆的长轴为，短轴为，取椭圆内点为坐标原点建立直角坐标系。假设平行于轴和轴的各断面上漆膜的厚度分布均服从指数为1和2的分布函数，并且在同一截面上的值是相同的。假设喷涂区域内任意一点A(,)到轴的距离是，到轴的距离是，过该点分别做轴轴的垂线，与椭圆的交点分别为12和12，与轴轴的交点分别为，，见图4。

根据分布模型的喷枪椭圆形喷幅示意图进行理论推导可得漆膜厚度模型为：

(1)

图4 β分布模型的喷枪椭圆形喷幅示意

Fig.4 Schematic diagram of elliptical spray amplitude distribution of β distribution

自动旋转式喷涂机在工作过程中喷枪以恒定的角速度旋转，木门以恒定的速度进给，那么每个截面的漆膜厚度分布基本不变，因此根据椭圆双分布模型的推导公式可得到木门表面漆膜速率累积的分布模型。

(2)

式中：qmax为最大漆膜厚度(μm)；w为喷幅宽度(mm)；β为β分布函数中的一个待定参数；x为喷涂区域内任意一点到喷枪在喷涂平面上投影点的水平距离(mm)。β分布模型漆膜厚度分布见图5。

希腊人的雕塑，如果用美感来评价，已经失于肤浅，因为古希腊的雕塑作品里展现的是人类精神的高贵。“掷铁饼者”向后抡起的手臂和曲膝扭转的态势永远让人感到一股势不可当的强力，维纳斯优美的“S”型的站姿和残缺的手臂令人遐想无穷。权力可以更迭，但希腊人所创造的文明却永不磨灭。

图5 漆膜累积速率 Fig.5 Diagram of film accumulation rate

2.2 喷涂厚度模型参数求取

基于漆膜喷涂厚度试验建立的β分布模型，可根据最小二乘法选取适应度函数，即以实际的喷涂厚度和对应点的模型计算出的值差的平方最小建立优化模型。

(3)

式中：qi为xi处的试验数据(μm)；q(xi)为根据式（2）计算得到的数据(μm)。

采用Matlab遗传算法工具箱对优化模型进行求解。将试验数据（部分数据见表1）进行计算，得到qmax=15.102，w=346.165，β=3.226。

漆膜的理论模型为：

(4) 将得到的β分布模型的参数代入式（2），即得到漆膜表面的喷涂理论模型。将得到的喷涂模型与实际的测量数据进行比较，结果见图6。 图6 漆膜厚度拟合 Fig.6 Fitting diagram of film thickness 从图6中可以看出，通过β分布模型得到的漆膜厚度与实际漆膜的测量厚度基本一致，因此该模型可以表示木门表面的漆膜厚度分布情况。 2.3 喷枪喷涂轨迹确定 文中喷涂以木门喷涂为例，喷涂机在喷涂过程中，木门在传送带的作用下做直线进给运动，喷枪在旋转架上做顺时针的旋转运动。假设木门静止，由此可知，单支喷枪的喷涂轨迹由木门水平方向的运动和旋转架的旋转运动合成。喷涂机的旋转半径R=500 mm。自动旋转式喷涂机喷涂过程见图7。 喷枪的运动速度： (5) 图7 自动旋转式喷涂机喷涂 Fig.7 Spraying diagram of automatic rotary sprayer 由此可以得出喷枪的运动轨迹： (6) 求解可以得出： Escalator system length Ls and split section length A1, A2(including manual input split section length A1, A2) are calculated from SAP system. (7) 由t=0时刻喷枪的初始位置可以得出： (8) 最终喷枪的运动轨迹为： (9) 式中：vt为木门的进给速度(mm/s)；vr为旋转架的旋转速度(r/min)；R为旋转架的旋转半径；ω为旋转架的角速度(rad/s)。 使用Matlab软件对喷枪的喷涂轨迹进行编程，可得到初始位置喷枪的喷涂轨迹见图8，双支喷枪的喷涂轨迹见图9。 2.2 下载频次 54篇高被引论文的总下载频次为45 839次，单篇最高下载频次为4 194次（对应的被引频次为104次），单篇最低下载频次为81次（对应的被引频次为20次），平均下载频次为849次∕篇。其中，下载频次＞2 000次的论文有3篇，500次＜下载频次≤2 000次的论文有26篇，100次＜下载频次≤500次的论文有23篇，下载频次≤100次的论文有2篇。 随着乞讨合法化政策在伦敦这座城市的执行，麦克尤恩为读者展示了一种违背社会伦理的城市空间的荒原镜像：人们对乞讨时产生的道德羞耻感逐渐消失了，施舍不再是一种道德高尚的绅士行为，乞讨变成了一种正式的社会职业。这样的社会犹如丛林法则盛行的荒蛮世界，没有公认规则，没有统一标准，没有伦理善恶，人们做的一切活动，就只是为了一个简单的目的——生存下去。在这样的社会中，麦克尤恩用细腻的笔触为读者描绘了一个少女乞丐形象，再次借用“他者”的视角来对这种社会空间的荒原镜像进行尖锐的批评。 由图8可知，喷枪的喷涂轨迹为螺旋线，为保证喷涂表面厚度的均匀性，应该合理地规划出下一支喷枪的进入待喷涂工件的位置，即合理地规划出2条喷枪轨迹间的距离。 图8 初始位置喷枪喷涂轨迹 Fig.8 Diagram of spray gun spraying trajectory in initial position 图9 双支喷枪喷涂轨迹 Fig.9 Diagram of dual spray gun spraying trajectory 3 喷涂轨迹模型的优化 文中运用木门表面漆膜的生长速率模型来确定喷涂间距。自动旋转式喷涂机的喷涂轨迹见图8。根据实际情况可知，喷涂机的旋转直径大于待喷涂的工件的宽度，因此可以忽略待喷涂工件外轨迹交叉的部分。喷枪在工件范围外时不喷涂，避免了涂料的浪费。根据图9所示的喷枪喷涂轨迹分析可知，木门表面上漆膜厚度的形成可看认为是单支喷枪进行多次螺旋线轨迹喷涂形成的，为了保证漆膜厚度的均匀性，要合理规划出2条喷涂轨迹间的距离，因此需要建立喷涂轨迹间距搭接的漆膜厚度优化模型。可将喷枪的喷涂轨迹简化成图10—11，即单支喷枪沿着2种旋向进行了多次喷涂完成了整个木门表面的喷涂过程。喷涂机的螺旋线型喷涂轨迹简化为了2次圆弧型的轨迹喷涂，因此只需对其中的单次喷涂轨迹间距进行合理的规划就能保证漆膜厚度的均匀性。于是以木门表面漆膜厚度最均匀和喷涂时间最短为优化目标，基于喷涂轨迹间距d建立优化模型，以木门的进给速度v和喷涂机的旋转速度为优化变量，以木门的长度L、喷涂机的旋转半径R、喷涂机的角速度为设计变量。以搭接优化模型上每个点的漆膜厚度与期望厚度q(d)之差小于最大允许偏差作为约束条件，建立喷涂轨迹间距离为d的优化模型进行求解。 图10 下侧进入喷枪轨迹 Fig.10 Diagram of lower entry gun track 图11 上侧进入喷枪轨迹 Fig.11 Diagram of upper entry gun track 3.1 喷涂轨迹间距搭接的优化模型 合理的规划喷涂间距能够保证喷涂漆膜厚度的均匀性和最大的喷涂效率。选择木门表面上的某一点的漆膜厚度作为分析。该点的漆膜搭接厚度分布见图12。 图12 漆膜重叠区域厚度分布 Fig.12 Thickness distribution in overlapping area of paint film 木门上任一点处的漆膜厚度为： 2017年，诸暨市出台《行政机关行政调解权力义务清单》，厘清了行政机关的行政调解职责，落实行政调解责任。清单共梳理出各行政机关的行政调解权力义务52条，涉及20个行政管理部门。与此同时，该市力推人民调解与行政调解的联动，在公安派出所、交警队等机构，都设置了人民调解工作室，受委托从事相关民事纠纷的调处。 (10) 根据漆膜重叠区域厚度分布，可知要想保证木门表面漆膜厚度的均匀性，就要使漆膜在处的累积厚度和,处的厚度差最小。 男人放肆地笑了笑说：“好好，不说这个！不说这个了！我就喜欢你这样懂事的女人，从不和我家里的那个黄脸婆争风吃醋。宝贝儿，我不会亏待你的。” (11) 根据自动旋转式喷涂机的喷涂轨迹关系可得： (12) (13) 因此一扇木门喷涂的时间为： (14) 为了保证木门表面漆膜厚度的均匀性，叠加模型的漆膜厚度应该与期望的厚度之差小于最大允许偏差，即： 在本次设计中，把室温标准值与当前室温值的差值e和差值变化率ec作为输入值，输出值取PID控制器的三个参数Kp、Ki、Kd的偏移量，其中Kp控制器的比例系数，Ki为控制器的积分系数，Kd为控制器的微分系数。系统模糊PID控制图如图3所示。 (15) 求解漆膜搭接模型的多目标表示式为： (16) 3.2 基于NSGA-Ⅱ算法对喷涂轨迹搭接模型求解 目前，多目标优化问题求解的算法众多，主要有多目标蚁群算法、多目标粒子群算法、NSGA-Ⅱ算 法[17]等。其中NSGA-Ⅱ算法是采用精英策略的快速非支配排序算法，在求解多目标优化的问题中是比较有效的。NSGA-Ⅱ算法优化求解流程见图13，其具体求解方法如下所述。 1）生成初始种群。随机生成染色体序列，并判断是否满足式（16）的约束条件，若不满足，则重新生成染色体。 从形式上来讲，会计监督体系可以分为企业内部的会计监督和企业外部的会计监督。为进一步完善现代化企业制度的会计监督体系，需要从以下两个层面入手。 2）适应度函数与快速非支配排序。将目标函数作为适应度函数，进行非支配个体分层排序。比较个体间的支配与非支配关系，找到所有支配个体，将其作为第1级非支配层。对于剩下的个体重复上面的操作，找到第2层非支配层。依此类推，直至所有个体均被分层。 经过隋朝两代帝王的相继开凿,广通渠、永济渠、通济渠、邗沟、江南河等运河,形成了完备的沟通关中与魏、齐旧地和梁、陈旧地的水上交通体系。 3）拥挤度计算。在个体在完成非支配排序和拥挤度计算后，对个体的非支配排序序号进行比较。若2个个体非支配排序序号不同，则取非支配排序序号小的个体，若2个个体在同一级，则取周围拥挤程度小的个体。 4）拥挤度比较。任选2个个体，若非支配排序序号不同，则选取序号小的个体；若序号相同，则选取周围较不拥挤的个体。 图13 NSGA-Ⅱ算法求解流程 Fig.13 Solution flow chart of the NSGA-Ⅱ algorithm 5）设置参数。种群规模800，最大遗传代数为200，变异概率为0.1，杂交概率为0.8。 本文综述了瘦素对水生动物代谢、生长发育和繁殖的影响及其机理研究进展，旨在深入理解和研究之，以便更好地利用瘦素，调控水生动物代谢、生长发育和繁殖，促进养殖渔业的健康快速发展，提高经济效益和社会效益。 运行Matlab程序后得到16组非劣解，其结果见表2。 3.3 结果分析 从表2中可以得出，优化目标4的漆膜厚度差为0.138 μm，需要的喷涂时间为6.995 s，此时的漆膜厚度差值最小，喷涂的效果是最均匀的。与其他组非劣解相比，这一优化目标的漆膜厚度最均匀，喷涂效率也相对较高，因此优化目标4的优先级更高。最终确定木门的进给速度为428.849 mm/s，喷涂机的旋转速度为6.22 rad/s。 根据优化出的木门进给速度和喷涂机的旋转速度，实现了对自动旋转式喷涂机喷涂轨迹规划。通过Matlab软件进行漆膜厚度仿真，得到的漆膜厚度见图14。从图14中可以看出漆膜厚度较为均匀，说明计算结果可靠。 表2 优化后的非劣解 Tab.2 Non-inferior solution after optimization 序号目标1 k1/μm目标2 T/s最佳速度v/(mm·s−1)最佳转速/(rad·s−1) 19.3345.021428.8496.228 28.4685.226574.0276.106 35.9195.643531.666.244 40.1386.995428.8496.22 57.0875.487546.7166.092 61.0826.802441.0596.104 75.3725.797517.5496.146 83.5066.182485.2756.166 92.6596.409468.0596.101 1026.623452.9696.002 114.755.97502.5546.053 122.1426.497463.0546.206 136.8145.529542.5476.114 140.6396.912434.0536.122 155.3595.799517.2996.146 167.7235.296566.4486.26 图14 漆膜厚度仿真 Fig.14 Simulation of film thickness 4 结语 文中建立的木门表面漆膜厚度分布模型，能够较好地反映木门表面的实际喷涂厚度。根据相对运动关系确定了自动旋转式喷涂机喷涂轨迹，根据喷涂轨迹建立了漆膜搭接的优化模型。通过NSGA-Ⅱ算法对漆膜搭接模型进行优化，确定了木门的进给速度为428.849 mm/s，喷涂机的旋转速度为6.22 rad/s。通过Matlab仿真验证了漆膜厚度的均匀性。为实现包装领域内木门生产线的自动化喷涂作业做好了前期准备。 参考文献： [1] 李博, 张占宽. 木门旋杯式静电喷涂漆膜厚度的理论分析[J]. 林业科学, 2018, 54(5): 109-115. LI Bo, ZHANG Zhan-kuan. Theoretical Analysis of Film Thickness of Rotary Cup Electrostatic Spraying for Wooden Door[J]. Scientia Silvae Sinicae, 2018, 54(5): 109-115. [2] 刘慧, 杨炙坤. 四自由度包装搬运机械手控制系统设计[J]. 包装工程, 2017, 38(5): 30-33. LIU Hui, YANG Zhi-kun. Control System Design of 4-DOF Packaging Handling Manipulator[J]. Packaging Engineering, 2017, 38(5): 30-33. [3] 郑悠, 方丹丹, 曾春年. 基于离线编程技术的喷涂机器人第七轴开发[J]. 电子技术应用, 2017, 43(5): 15-20. ZHENG You, FANG Dan-dan, ZENG Chun-nian. Development of Seventh Axis of Spraying Robot Based on Offline Programming Technology[J]. Application of Electronic Technique, 2017, 43(5): 15-20. [4] 李翠明, 龚俊, 牛万才, 等. 基于改进隶属云模型蚁群算法的喷涂机器人喷枪轨迹组合优化[J]. 上海交通大学学报, 2015(3): 99-103. LI Cui-ming, GONG Jun, NIU Wan-cai, et al. Combination Optimization of Spray Gun Trajectory of Spray Robot Based on Improved Ant Colony Algorithm of Subjection Cloud Model[J]. Journal of Shanghai Jiaotong University, 2015(3): 99-103. [5] ZHONG Yun, ZHOU Shu-mei. Path Planning for Spray Painting Robot of Horns Surfaces in Ship Manufacturing[J]. IOP Conference Series: Materials Science and Engineering, 2019, 521(1): 12015. [6] LI C, ZHANG Y. Trajectory Optimization of Spraying Manipulator for Large HullSection[C]// IEEE International Conference on Information & Automation, IEEE, 2017: 1438-1443. [7] GUAN L, CHEN L. Trajectory Planning Method Based on Transitional Segment Optimization of Spray Painting Robot on Complex-Free Surface[J]. Industrial Robot, 2019(13): 31-43. [8] 马淑梅, 罗曦, 李爱平, 等. 船舶工业机器人曲面喷涂喷枪轨迹离线规划[J]. 同济大学学报(自然科学版), 2017(2): 289-295. MA Shu-mei, LUO Xi, LI Ai-ping, et al. Off-Line Planning of Spray Gun Trajectory for Curve Spraying of Shipbuilding Industrial Robot[J]. Journal of Tongji University(Natural Science), 2017(2): 289-295. [9] 陈雁, 胡俊, 张钢, 等. 球形面喷涂成膜特性研究[J]. 湖南大学学报(自然科学版), 2019, 46(6): 42-51. CHEN Yan, HU Jun, ZHANG Gang, et al. Study on Film Forming Characteristics of Spherical Surface Spraying[J]. Journal of Hunan University (Natural Science Edition), 2019, 46(6): 42-51. [10] TENG K, ZENG Y. The Path Optimization of Spray Painting Robot for Two Path Pattern[J]. Advanced Materials Research, 2012, 605-607: 1563-1567. [11] GIULIO T, PAOLO B, LORENZO S, et al. A New Path-Constrained Trajectory Planning Strategy for Spray Painting Robots-rev.1[J]. International Journal of Advanced Manufacturing Technology, 2018, 98: 2287-296. [12] 朱由锋, 刘新华, 王强, 等. 喷涂机悬臂梁的正弦激励参数振动分析[J]. 包装工程, 2020, 41(13): 223-230. ZHU You-feng, LIU Xin-hua, WANG Qiang, et al. Vibration Analysis of Sine Excitation Parameter of Sprayer Cantilever Beam[J]. Packaging Engineering, 2020, 41(13): 223-230. [13] ARYA V, TAHERI E, JUNKINS J L. A Composite Framework for Co-Optimization of Spacecraft Trajectory and Propulsion System[J]. Acta Astronautica, 2021, 178(6): 773-782. [14] ARNOLD B C, HECTOR W, GOMEZ, et al. Univariate and Bivariate Models Related to the Generalized Epsilon-Skew-Cauchy Distribution[J]. Symmetry, 2019, 11(6): 794-794. [15] 王国磊, 陈恳, 陈雁. 变参数下的空气喷枪涂层厚度分布建模[J]. 吉林大学学报(工学版), 2012, 42(1): 188-192. WANG Guo-lei, CHEN Ken, CHEN Yan. Modeling of Coating Thickness Distribution in Air Spray Gun with Variable Parameters[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(1): 188-192. [16] ARIKAN T B A S. Modeling of Paint Flow Rate Flux for Circular Paint Sprays by Using Experimental Paint Thickness Distribution[J]. Mechanics Research Communications, 1999: 609-617. [17] DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. Optimization of Spraying Trajectory of Automatic Rotary Sprayer LI San-ping, DU Jia-bao, YANG Chun-mei, REN Chang-qing, ZHANG Qing-ming, HOU Yu-ning (Northeast Forestry University, Harbin 150040, China) ABSTRACT: The work aims to realize automatic and efficient coating operation on the packaging production line, establish a paint film thickness distribution model on the surface of the workpiece to be sprayed, optimize the spraying trajectory, solve the best feed speed of the workpiece to be sprayed and the rotation speed of the automatic rotary sprayer, and realize the optimization of the spraying trajectory of the automatic rotary sprayer. Firstly, the experimental data on the thickness of the paint film were obtained by the automatic rotary sprayer. The experimental data were characterized by the β-distribution model. Key parameters of the β-distribution model were fitted by the Matlab genetic algorithm toolbox. The spraying trajectory equation was determined according to automatic rotary sprayer spraying process. On this basis, the film thickness lap model was established. The best feed speed and the rotation speed of the sprayer were solved through the NSGA-Ⅱ algorithm. According to optimization with the NSGA-Ⅱ algorithm, the feed speed of the workpiece to be sprayed was 428.849 mm/s, the rotation speed of the sprayer was 6.22 rad/s, the spraying time was 6.995 s. The film thickness model of the sprayed surface can accurately reflect the actual spraying situation of the sprayed surface of the workpiece, and can reasonably optimize the spraying trajectory of the automatic rotary sprayer. It lays a foundation for realizing automatic spraying operations in packaging. KEY WORDS: film thickness distribution; β distribution model; genetic algorithm; NSGA-Ⅱalgorithm 中图分类号：TB486 文献标识码：A 文章编号：1001-3563(2022)01-0228-08 DOI：10.19554/j.cnki.1001-3563.2022.01.029 收稿日期：2021-06-05 基金项目：黑龙江省应用技术研究与开发计划（GA19A402）；中央高校基本科研业务费专项资金（2572020DR12）；中央高校基本科研业务费专项资金（2572014BB06） 作者简介：李三平（1981—），女，博士，东北林业大学副教授，主要研究方向为机械系统仿真技术。