无伞空投储液罐的高空跌落仿真分析
张宇婷,耿小凯,任春华,计宏伟
无伞空投储液罐的高空跌落仿真分析
张宇婷1,耿小凯2,任春华1,计宏伟1
(1.天津商业大学,天津 300134;2.河北金后盾塑胶有限公司,河北 邢台 054000)
为提高液体类空投物资补给效率,研究椭球型结构的无伞空投储液罐跌落冲击地面过程的力学响应。基于欧拉-拉格朗日耦合算法,建立含有内盛物的椭球形储液罐有限元模型,通过Abaqus CAE仿真跌落得到罐壁材料层为聚乙烯-发泡-聚乙烯在不同厚度比条件下含内盛物跌落的最大等效塑性应变(简称最大塑性应变)云图、应力-时间曲线。不同层间厚度比与储液罐的最大塑性应变、塑性应变的时间和应变集中区域有密切联系,当厚度比为1∶2∶1时,罐体达到最大塑性应变的时间短,把手部位出现应变集中现象的概率增大;厚度比为1∶1∶2时,罐体的塑性应变相对降低,抗冲击能力没有达到理想优化效果;厚度比为1∶1∶2时,罐体的塑性应变最小,在此情况下能承受的冲击地面的瞬时速度最大,罐体的结构性能最好。基于此提出了一种结构优化思路,在添加中间发泡层以减轻配重的基础上,适当增加外层聚乙烯材料的厚度或者使用缓冲性能更好的材料,增加罐壁的缓冲吸能,改善材料结构强度。
无伞空投;储液罐;有限元模拟;力学响应;等效塑性应变
空投是通过直升机等航空装置将指定运输的装备物资从空中投送到预定地点的过程,是一种方便、快捷、高效的物资运输方式。空投技术不仅是作战过程中输送武器装备和物资器材的主要方式,也是应对自然灾害过程中物资投送的重要保障手段[1—3]。2008年汶川大地震的抗震救灾行动中,为迅速实现救援任务,中国军队派出大量运输机和直升机采用空降空投的方式来向灾区运送救灾物资,保障灾区人民的生活和医疗卫生的需求。目前,有伞空投是进行物资装备运输的主要投送形式,其具有前期准备工作繁杂、降落伞使用成本高等缺点,造成资源的大量浪费,同时受气候、地面环境等因素影响,在应对某些自然灾害时有伞空投不能及时有效地投送应急物资装备。随着包装防护技术和缓冲材料技术的发展,以及在实际作业中对安全高效的需求不断提高,无伞空投技术因其包装简单、资源利用率高、受环境因素影响小、实施迅捷等特点逐渐受到学者们的重视,成为国内外学者的研究热点[2—4]。目前,无伞空投的研究主要集中在两大方面:空投装备的结构优化[5—6]和研制更加可靠耐用的缓冲装置[7—12]。
在无伞空投中,椭球形储液罐广泛用于液体类应急物资的运输,文中选用的储液罐主要材质为高密度聚乙烯,罐壁为3层材料结构,中间材料为发泡结构,用以减轻配重和吸收冲击能量,罐体表面具有均匀分布的加强肋结构,能够增加整体的抗冲击性能。为了验证无伞空投储液罐的实用性、有效性和可靠性,需要进行大量的试验验证,而进行空投试验往往需要耗费大量的人力物力,且每次试验跌落对储液罐具有一定的破坏性,导致试验所需的研究成本较高。随着有限元技术的发展和完善,计算机仿真模拟因其方便可靠的优点逐渐成为研究空投跌落动力学响应的重要研究手段[13—15]。模拟过程采用以下假设进行建模。
1)空投装备的缓冲完全靠罐体产生,不考虑降落的气动阻力,没有附加其他的缓冲装置。
2)罐体内部各处压力相同且罐体壁厚均匀。模拟过程中罐体等效为理想化模型,不考虑由于制作工艺带来的误差。
3)罐体主要由3层材料组成,且均假设厚度均匀,3层材料总厚度为0.02 m。跌落时视作1个整体,即跌落过程中各部分连接紧密,忽略材料层与层之间连接力的影响。
建模时默认罐体为塑性材料,具有理想塑性行为。文中以椭球形无伞空投储液罐为研究对象,基于欧拉-拉格朗日耦合方法进行建模,结合Abaqus CAE软件,在保证总厚度固定的条件下,改变储液罐3层材料结构的层间厚度比,模拟其跌落力学响应,并进行深入研究,对比分析不同层间厚度比对罐体性能的影响,根据应变分布特征进行弹塑性分析,为有效进行液体类应急物资无伞空投的缓冲包装设计提供理论参考。
1 有限元模型
1.1 储液罐结构和材料参数测量
在空投着陆瞬间,罐体受极大的冲击载荷作用,容易造成较大的变形和塑性硬化,对于结构的强度、缓冲性能、抗冲击性能等提出来很大的要求。文中对3种层间厚度比的椭球型储液罐冲击地面过程进行模拟,并将模拟结果进行对比分析,评价罐体的结构性能。
罐体材质为高密度聚乙烯,采用一体成型的椭球形结构;所有棱角均圆角化,缓解罐体与地面接触产生的应力集中现象;跌落时罐体的3层结构材料缓冲吸能,无其他缓冲装置。
罐体包括3层材料[4],其结构见图1,3层材料结构见图2。罐壁最外层原料与最内层原料均为高密度聚乙烯(密度为950 kg/m3),内外层聚乙烯材料的基本力学参数见表1。中间缓冲层为发泡材料(密度为166 kg/m3),用来降低罐体总质量并吸收冲击。在Abaqus模拟前,为保证模拟结果的准确性,在进行中间发泡层的材料定义时,中间层材料的性能依据塑料拉伸性能试验标准(GB/T 1040.1—2018),通过万能试验机进行单轴拉伸试验测得,直接将处理得到的名义应力应变数据输入Abaqus材料库中进行仿真分析,具体参数见表2。
模拟过程中,采用饮用水为主要内盛物,其密度为996 kg/m3,粘度为0.01 Pa·s,体积模量为2.094 GPa。
1.2 流固耦合方法
无伞空投储液罐跌落模拟采用流固耦合方法,将罐体作为固体域与罐内饮用水作为流体域进行物理场耦合,并利用分离解法求取控制方程,完成流固耦合交界面的数据传递。
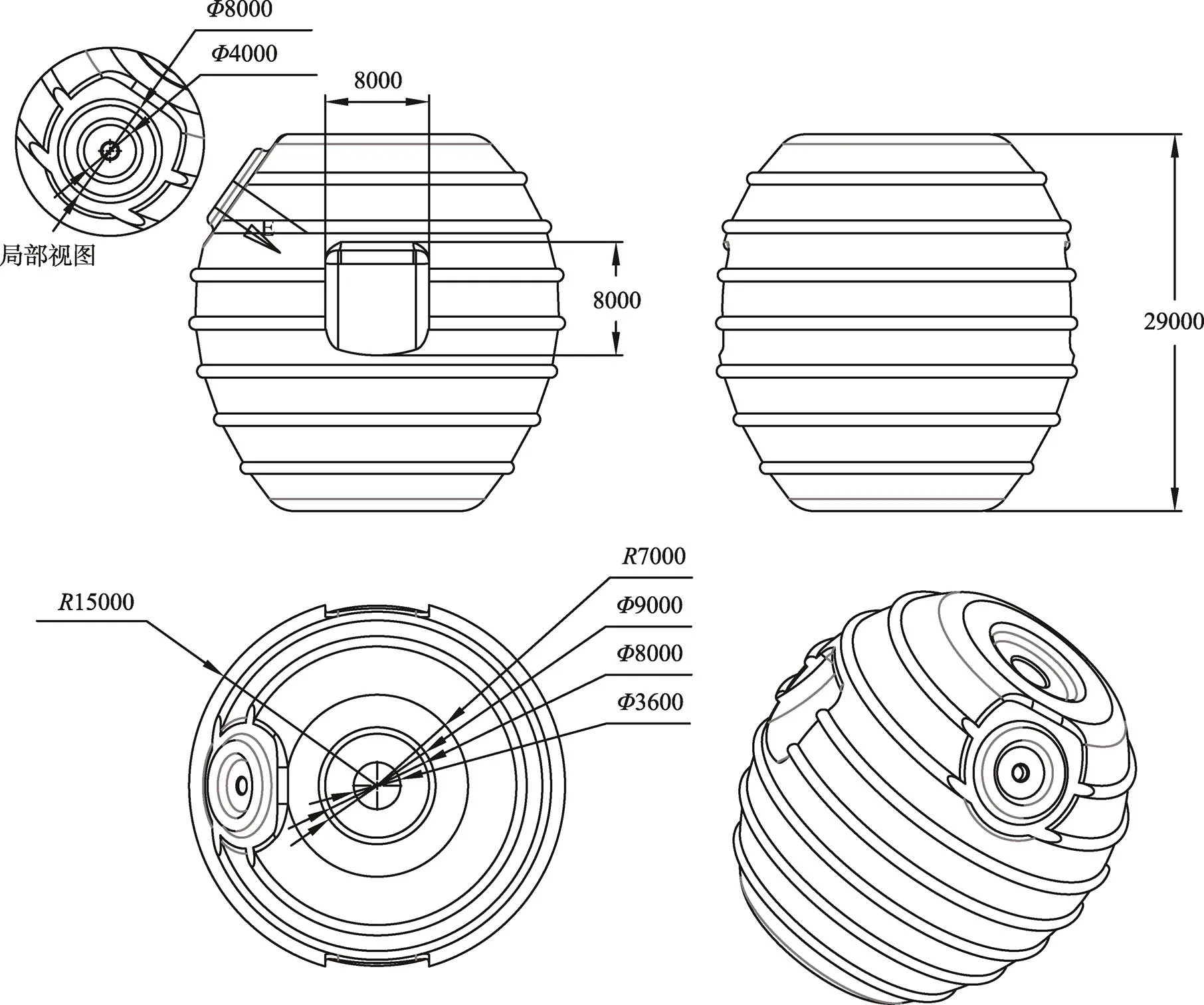
图1 空投储液罐结构
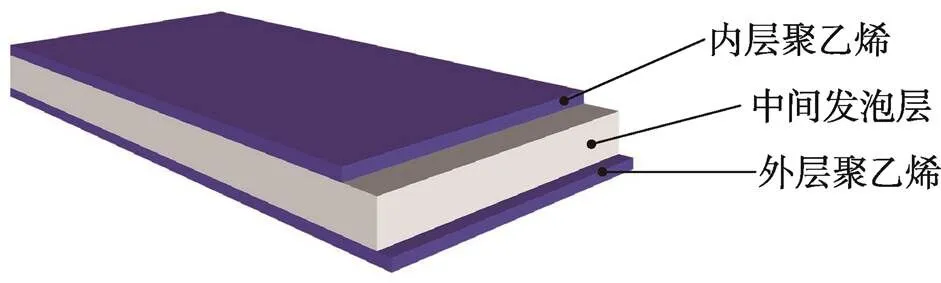
图2 3层材料结构

表1 聚乙烯材料参数
连续性方程见式(1):
(1)
式中:为流体密度;U为质点的速度矢量;x为空间坐标矢量。
动量方程(N-S方程)见式(2):
(2)
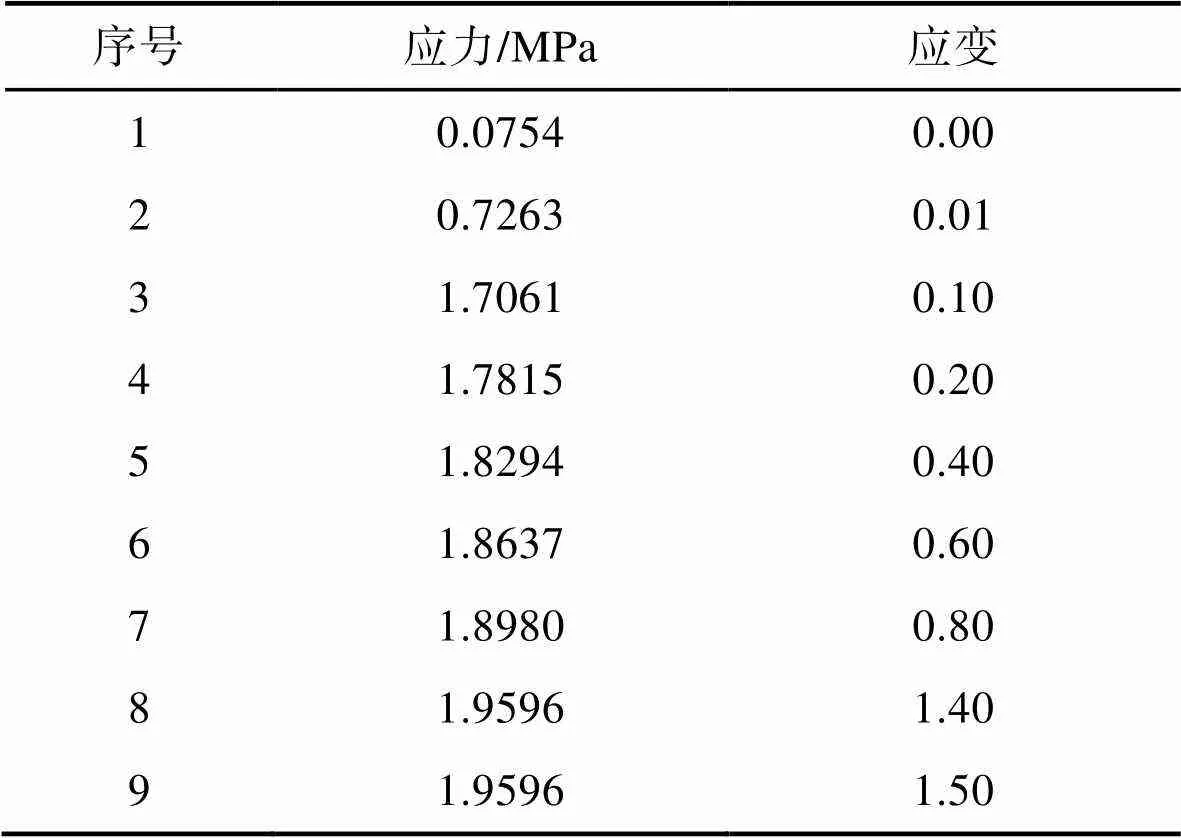
表2 中间发泡层材料非线性应力-应变参数值
式中:和为质点的速度矢量;和为空间坐标矢量;M为变形速率张量。
能量方程:
(3)
式中:为热传导系数;为流体温度。
固体控制方程:
(4)
式中:s为固体介质密度;s为固体厚度。流固耦合遵循守恒原则。
为保证计算精度和效率,选用CEL方法进行跌落运动的流固耦合分析。文中所述罐体整体为六面体结构化网格,按照实体内外层的厚度将罐体模型分为3层,均采用拉格朗日单元建模,3层结构的单元类型均为C3D8R,分别进行每层材料的参数定义;液体内盛物采用欧拉单元建模(3D,Eulerian),单元类型为EC3D8R。
流固耦合过程中建立罐体内液体的初始形状,通过体积分数工具(Volume Fraction Tool)定义欧拉体的初始流域,同时将流体材料赋予给欧拉网格。欧拉体的尺寸设置为500 mm×500 mm×500 mm正方体空间,包围整个跌落系统,与地面的接触为显示通用行为接触(General contact,Explicit),整体装配见图3。整个仿真过程采用显式动力学(Dynamic Explicit)模块进行,包括35 937个欧拉单元和115 056个拉格朗日单元。

图3 流固耦合模型
1.3 跌落工况模拟
无伞空投技术属于中高空物体跌落,跌落过程近似于自由落体。借助Abaqus CAE有限元分析软件,按照接触地面不同的瞬时速度值进行储液罐的跌落仿真分析。跌落过程的模拟需要创建刚性地面部件,地面材质为混凝土,部件类型为均质壳体表面(Deformable Shell Planar),弹性模量为20 GPa,泊松比为0.15,密度为2500 kg/m3。为了分析材料层对储液罐性能的影响,保持总厚度值不变,改变3层结构厚度值进行模拟,建立内层聚乙烯-中间发泡层-外层聚乙烯厚度比为1∶2∶1(Ⅰ类)、2∶1∶1(Ⅱ类)和1∶1∶2(Ⅲ类)的3种分析工况。
参考弹塑性失效设计准则,以应力下降至强度极限的10%之前最后记录的数据点对应的应变为材料断裂标称应变,罐体等效塑性应变(PEEQ,简称最大塑性应变)为:
(5)
罐体材料最大等效塑性应变必须满足条件:
(6)
式中:ε为材料的最大等效塑性应变;tb为材料的断裂标称应变。经计算得到,该类聚乙烯材料断裂标称应变为0.1929,对应应力为32.0367 MPa,对应的总应变为0.2141。
2 结果与讨论
2.1 Ⅰ类储液罐跌落的仿真分析
现有的储液罐材料结构的层间厚度比近似为1∶2∶1,首先通过Abaqus CAE软件对储液罐的空投过程进行模拟仿真试验,并提取出储液罐以不同瞬时速度(9.9,14.0,17.1,19.8,22.1,24.2 m/s)冲击地面的最大塑性应变和所用时间,详细结果见表3,储液罐危险点位置达到最大等效塑性应变时刻云图见图4。由表3可知,该时间规律呈线性变化且逐渐降低;同时瞬时冲击速度与最大塑性应变具有直接联系,最大塑性应变随瞬时速度的增加呈递增关系。同时由等效塑性应变云图可知,罐体在跌落时,主要变形位置均在罐体底部,整体未发生较大变形或破坏;当冲击速度为24.2 m/s时,只有局部位置有较大的等效塑性应变,难以出现明显破损现象,这符合聚乙烯材料的高弹塑性[17]。

表3 Ⅰ类储液罐的塑性应变参数
在储液罐冲击地面过程中,罐体底面将率先接触地面,应变区域主要集中在底部倒角处。由图5a可知,为了便于分析3层材料结构的受力情况,在罐体中间截面上作法线′,使其与倒角处曲率半径重合且过倒角中心点。在直线′上选取位于罐体壁上外层、中层、内层这3个位置的单元节点(单元节点1、单元节点2、单元节点3),在模拟结果中提取各个单元节点以瞬时速度为24.2 m/s冲击地面情况下的节点应力随时间的变化情况。罐壁上外、中、内3层材料单元的应力-时间曲线见图5b。由曲线图可知,罐体该部位单元节点应力值均未超过屈服极限,内壁单元节点的应力值最高,外壁次之,中间发泡层的应力值最低。这是由于内壁同时受到跌落造成外部冲击和内部液体流动产生的耦合作用,使得跌落过程中罐体内壁单元的应力值普遍大于外壁单元的应力值。
2.2 Ⅱ类储液罐跌落的仿真分析
在不改变总厚度的条件下,为了研究缓冲层厚度对冲击性能的影响,加大内层厚度,减小中间缓冲层厚度,使其厚度比为2∶1∶1进行跌落模拟。Ⅱ类储液罐以不同瞬时速度冲击地面的等效塑性应变云图见图6,储液罐等效塑性应变的详细参数见表4,其变化规律与2.1节工况下基本相同。塑性应变主要分布在罐体底部与地面接触位置周围,随着冲击速度增加,等效塑性应变逐渐增大,塑性应变区域增大。相较于2.1节Ⅰ类储液罐,应变集中现象改善,最大塑性应变增加趋势减缓,最大塑性应变出现的时间延迟,相同瞬时速度跌落产生的最大塑性应变增大,即允许的跌高降低。

图4 Ⅰ类储液罐的等效塑性应变云图

图5 Ⅰ类储液罐的单元节点选取与应力-时间曲线
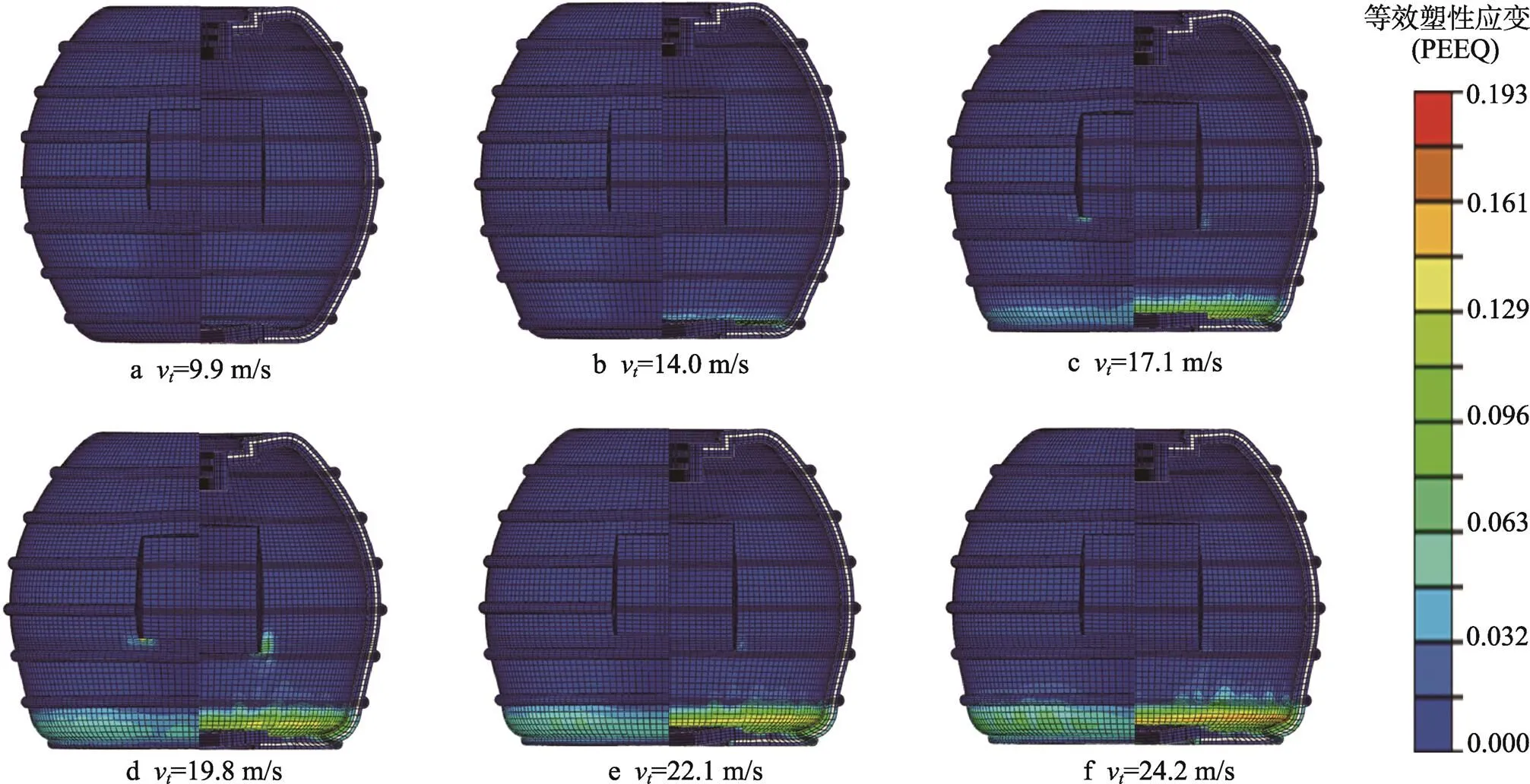
图6 Ⅱ类储液罐的等效塑性应变云图

表4 Ⅱ类储液罐的塑性应变参数
分析倒角位置的应力变化,见图7a,在直线′上选取位于罐体壁上外层、中层、内层等3个位置的单元节点(单元节点1、单元节点2、单元节点3)。储液罐以24.2 m/s冲击地面时3个单元节点的应力-时间曲线见图7b。罐体内壁单元节点的应力值最高,外壁次之,中间发泡层的应力值最低。同一位置内层单元应力仍然最大,同时最大应力在2.2 μs时超过材料强度极限。虽然该种材料结构能改善应变集中,但由于中间缓冲层厚度减小,发泡材料的吸能作用降低,使得罐体内壁所受冲击增大。
2.3 Ⅲ类储液罐跌落的仿真分析
在不改变总厚度的前提下,增大内层厚度,减小中间缓冲层厚度,使其厚度比为1∶1∶2进行跌落模拟,所得的等效塑性应变云图见图8,并提取出储液罐以不同瞬时速度冲击地面的详细参数,见表5。相较于前2种材料结构罐体的最大塑性应变明显降低,且均小于断裂标称应变。为找出该材料结构下储液罐塑性应变在弹塑性设计准则范围内的最大冲击速度,进一步改变速度值,计算塑性应变和损伤演变分析,当最大塑性应变小于断裂标称应变时,所对应的最大冲击速度值为26.2 m/s。
为了便于分析3层材料结构的受力情况,见图9a,在直线′上选取位于罐体壁上外层、中层、内层等3个位置的单元节点(单元节点1、单元节点2、单元节点3)。罐体以24.2 m/s速度冲击地面时3个单元节点的应力-时间曲线见图9b。由曲线图可知,当材料层厚度比为1∶1∶2时,同样是外部节点首先达到应力最大值,内部节点的应力值最大(31.16 MPa),未超过材料屈服极限,且达到最大值的时间明显延迟。
2.4 3种材料结构对比
对比3种材料结构以24.2 m/s速度冲击地面时的应力相关参数可知,液体空投罐的最大应力、应力变化和应变集中区域与材料层的厚度比有明显联系。由图10可知,从罐体单元达到最大应力值的时间上看,Ⅰ类储液罐应力在1.0 μs达到最大值,Ⅱ类储液罐应力在0.9 μs时刻达到最大值,Ⅲ类储液罐应力在2.5 μs时刻达到最大值;从最大应力值上看,Ⅰ类储液罐的最大应力为28.99 MPa,Ⅱ类储液罐的最大应力为36.21 MPa,Ⅲ类储液罐的最大应力为31.16 MPa,罐体的最大应力值较高。
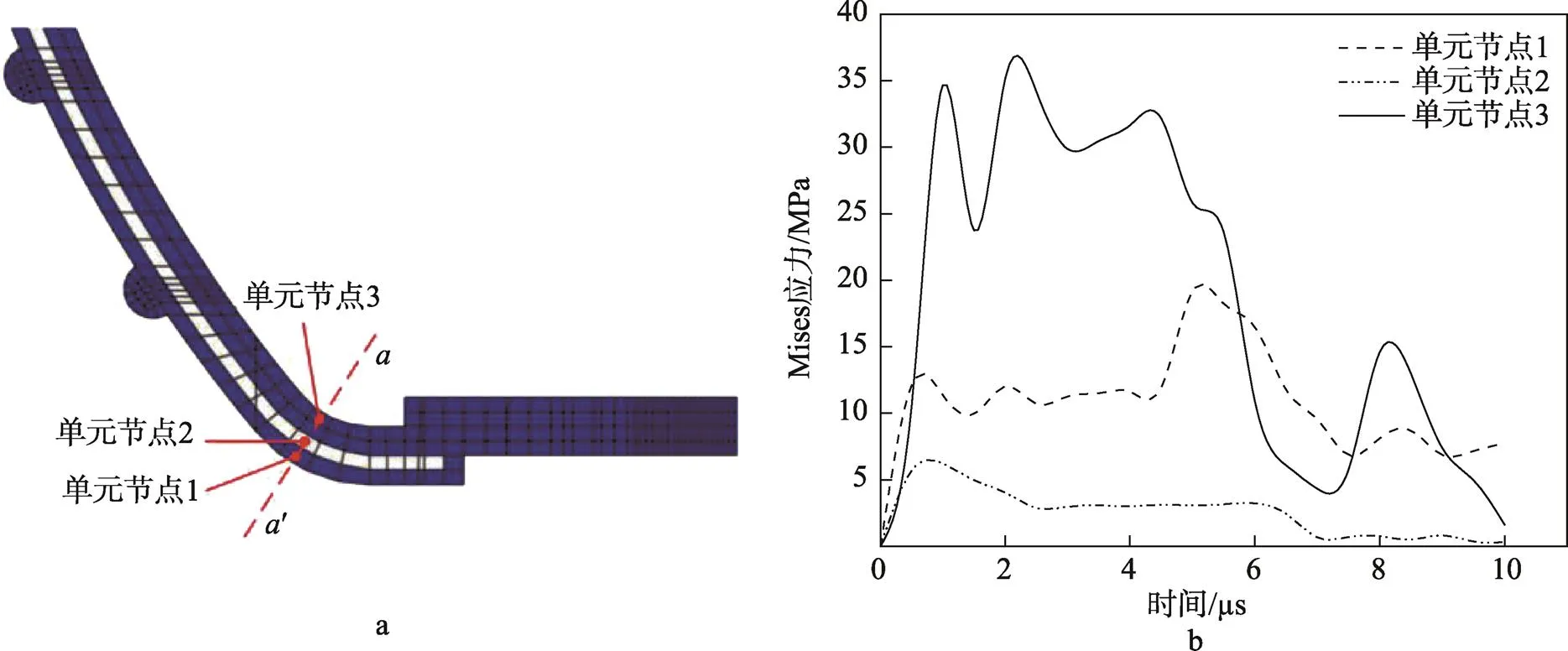
图7 Ⅱ类储液罐的单元节点选取与应力-时间曲线

图8 Ⅲ类材料结构储液罐的等效塑性应变云图

表5 Ⅲ类储液罐的塑性应变参数
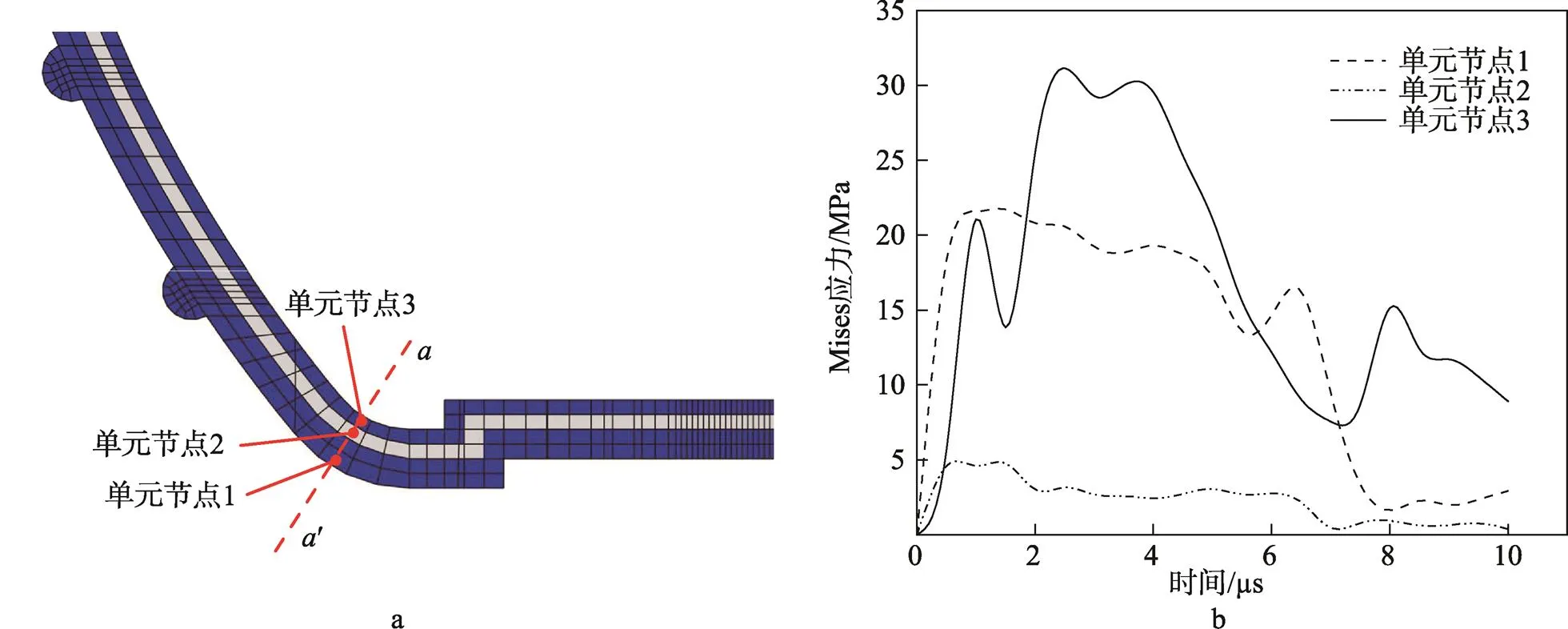
图9 Ⅲ类储液罐的单元节点选取与应力-时间曲线
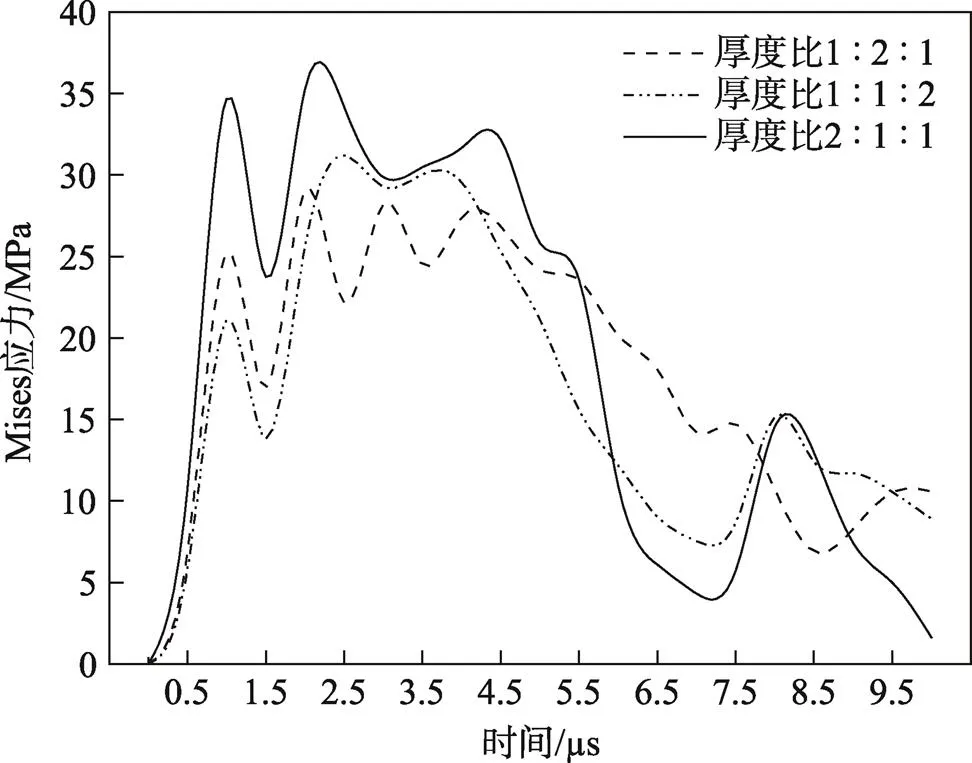
图10 3种材料结构的内层单元Mises应力
对比3种储液罐最大塑性应变达到断裂标称应变的跌落高度,Ⅰ类储液罐所能承受的最大冲击速度为23.2 m/s;Ⅱ类储液罐所能承受的最大冲击速度为22.6 m/s;Ⅲ类储液罐所能承受的最大冲击速度为26.2 m/s,很明显Ⅲ类储液罐在弹塑性理论范围内的承载能力和抗冲击强度最高。
对比3种储液罐在不同高度跌落的塑性应变数据,可以发现不同层间厚度比与罐体的最大塑性应变、塑性应变时刻和应变集中区域有明显联系。从最大塑性应变上看,Ⅰ类储液罐的最大塑性应变总体上小于其他2种材料结构的最大塑性应变;从达到最大塑性应变时间和应变区域上看,Ⅰ类储液罐达到最大塑性应变的时间较短,特殊部位容易出现明显的应变集中现象,Ⅲ类储液罐达到最大塑性应变的时间最长,其材料结构更好,可利用性更高。综上所述,适当增加中间缓冲层的厚度能够在一定程度上吸收跌落产生的冲击,减小内层应力;适当增加外层聚乙烯的厚度能有效降低罐体塑性应变,提高空投质量。由于把手部位的结构因素,在跌落时容易出现应力集中现象,尤其是当瞬时速度大于24.2 m/s时,此影响较为明显,因此将把手部位进行面倒圆处理能够在一定程度上改善结构强度,提高承载能力。
3 结构优化思路
参考上述模拟结果,文中提出从以下几方面提出结构优化的设计。
1)加纵向肋结构。为减缓罐体变形和内部液体流动造成的局部压力变大现象,避免液体空投罐在跌落瞬间产生较大变形发生破坏,最直接的方法是采取圆角化过渡、增加局部厚度等措施改良罐体结构。同时由结果云图显示,罐体肋部应变值明显小于其他部位,说明在罐体表面增加圆肋能有效增加罐体结构强度,提高抗冲击性能,可以考虑在罐体外壁增加纵向肋结构,进一步增强罐体的结构强度。
2)改变3层材料厚度比例。在添加中间发泡层以减轻配重的基础上,适当增加外层聚乙烯材料的厚度或者使用缓冲性能更好的材料,增加罐壁的缓冲吸能,改善材料结构强度。
4 结语
利用有限元分析技术对椭球形无伞空投橡胶液体空投罐进行了跌落模拟,通过Abaqus CAE软件建立了液体空投罐有限元模型,通过设置载荷和边界条件进行跌落分析,计算出全场的塑性应变分量和特殊节点的Mises应力-时间曲线,首先对现有的储液罐材料结构进行模拟计算,随后在保证总厚度不变的条件下改变3层材料厚度进一步模拟,得出以下结论。
1)对模拟结果进行对比分析发现,液体空投罐的3层材料厚度与其塑性应变和应变集中区域有明显联系,为液体类物资的无伞空投提供了有效的数据参考。
2)3层材料厚度比为1∶1∶2时罐体的塑性应变最小,在弹塑性理论范围内能承受的瞬时冲击速度最大,罐体的结构性能最好。
3)根据模拟结果提出了优化思路,适当增加中间发泡层与外层聚乙烯材料的厚度或者使用缓冲性能更好的材料,增加罐壁的缓冲吸能,改善材料结构强度。
[1] 邵朝俊. 我国重装空投系统现状和发展[C]//中国科协2002年学术年会, 2002: 1.
SHAO Zhao-jun.Current Status and Development of China's Heavy Equipment Airdrop System[C]//China Association for Science and Technology Annual Conference 2002,2002: 1.
[2] 赵西友, 王宏, 许涛, 等. 无伞空投缓冲包装材料及技术研究[J]. 包装工程, 2016, 37(3): 54-57.
ZHAO Xi-you, WANG Hong, XU Tao, et al. Free Drop Buffering Packing Material and Technology[J]. Packaging Engineering, 2016, 37(3): 54-57.
[3] 王铁宁, 刘磊. 陆军装备物资无伞空投系统设计[J]. 装甲兵工程学院学报, 2019, 33(2): 5-9.
WANG Tie-ning, LIU Lei. Design of the Army Equipment and Materials Airdrop without Parachute System[J]. Journal of Academy of Armored Force Engineering, 2019, 33(2): 5-9.
[4] 赵西友, 李彦平, 王静伟, 等. 滚塑无伞空投储水罐的设计与分析[J]. 中国塑料, 2019, 33(1): 111-115.
ZHAO Xi-you, LI Yan-ping, WANG Jing-wei, et al. A Design and Analysis of Rotationally Molded Water Storage Tank in Free Drop[J]. China Plastics, 2019, 33(1): 111-115.
[5] 易方, 孟浩龙. 新型空投橡胶油囊的设计[J]. 橡胶工业, 2018, 65(10): 1146-1149.
YI Fang, MENG Hao-long. Design of a New Type of Airdrop Rubber Fuel Drum[J]. China Rubber Industry, 2018, 65(10): 1146-1149.
[6] 刘胜祥, 王兴业, 徐丽丽, 等. 蜂窝纸板在空投包装中的应用[J]. 包装工程, 2016, 37(17): 25-29.
LIU Sheng-xiang, WANG Xing-ye, XU Li-li, et al. Application of Honeycomb Cardboard in Airdrop Packaging[J]. Packaging Engineering, 2016, 37(17): 25-29.
[7] 王新春, 马大为, 庄文许, 等. 某空投装备在不同缓冲装置下的冲击响应分析[J]. 包装工程, 2013, 34(13): 47-51.
WANG Xin-chun, MA Da-wei, ZHUANG Wen-xu, et al. Impact Response Analysis of Airdrop Equipment with Different Buffer Device[J]. Packaging Engineering, 2013, 34(13): 47-51.
[8] 许鑫. 冲压式快速空投缓冲气囊着陆过程仿真研究[J]. 机械工程与自动化, 2017(2): 59-60.
XU Xin. Simulation Research on Stamping Type Quick Airdrop Airbag Landing Process[J]. Mechanical Engineering & Automation, 2017(2): 59-60.
[9] TUTT B, SANDERS J, MYNENI S. Application of Optimization Software to Aid the Design of an Airbag Decelerator System[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, California, 2003: 1-8.
[10] 周默涵, 狄长春, 杨玉良, 等. 圆柱筒式空投气囊缓冲模拟[J]. 包装工程, 2017, 38(17): 128-132.
ZHOU Mo-han, DI Chang-chun, YANG Yu-liang, et al. Simulation of Cushion Characteristic of Cylindrical Airdrop Airbag[J]. Packaging Engineering, 2017, 38(17): 128-132.
[11] 孙宁国, 李良春. 空投着陆缓冲气囊研究现状[J]. 包装工程, 2017, 38(11): 97-101.
SUN Ning-guo, LI Liang-chun. Research Status of Airdrop Landing Buffer Airbag[J]. Packaging Engineering, 2017, 38(11): 97-101.
[12] XU Xin. Design and Analysis of Auto-Inflatable Air-Drop Cushion Airbag[J]. Mechanical Engineering & Automation, 2015, 6: 87-88.
[13] 杨佳, 赵春玲, 计宏伟, 等. 塑料和钢塑复合包装桶高温堆码强度模拟[J]. 包装工程, 2015, 36(15): 87-90.
YANG Jia, ZHAO Chun-ling, JI Hong-wei, et al. Simulation Analysis of High Temperature Stacking Strength for Palstic and Steel-Plastic Bucket[J]. Packaging Engineering, 2015, 36(15): 87-90.
[14] 刘永辉, 张银. 基于有限元分析的洗衣机跌落冲击仿真及改进设计[J]. 振动与冲击, 2011, 30(2): 164-166.
LIU Yong-hui, ZHANG Yin. Dropping Simulation and Design Improvement of a Washing Machine Based on FE Analysis[J]. Journal of Vibration and Shock, 2011, 30(2): 164-166.
[15] 张晓川, 任春华, 计宏伟, 等. 危险品包装用桶的跌落仿真分析[J]. 包装工程, 2016, 37(19): 116-120.
ZHANG Xiao-chuan, REN Chun-hua, JI Hong-wei, et al. Dropping Simulation Analysis of Dangerous Goods Packaging Buckets[J]. Packaging Engineering, 2016, 37(19): 116-120.
[16] 李亚飞, 孙小杰, 任月庆, 等. 滚塑用V-0级阻燃交联聚乙烯的制备及其性能研究[J]. 塑料工业, 2020, 48(8): 30-33.
LI Ya-fei, SUN Xiao-jie, REN Yue-qing, et al. Preparation and Properties of V-0 Grade Flame Retardant Crosslinked Polyethylene for Rotational Molding[J]. China Plastics Industry, 2020, 48(8): 30-33.
Simulation Analysis of Liquid Storage Tank for Free Drop
ZHANG Yu-ting1, GENG Xiao-kai2, REN Chun-hua1, JI Hong-wei1
(1.Tianjin University of Commerce, Tianjin 300134, China; 2.Hebei Jinhoudun Plastic Cement Co., Ltd., Xingtai 054000, China)
The work aims to study the mechanical response of the liquid storage tank with ellipsoidal structure for free drop during the process of falling and hitting the ground, in order to improve the replenishment efficiency of liquid airdrop supplies. Based on the coupling Euler-Lagrange algorithm, a finite element model of ellipsoid liquid storage tank was established. The drop process of the tank with different thickness ratios of polyethylene-foam-polyethylene was simulated by ABAQUS CAE to obtain the maximum equivalent plastic strain cloud diagram and stress-time curve. The thickness ratio between different layers is closely related to the maximum plastic strain, the time of plastic strain and the strain concentration area of the storage tank. When the thickness ratio is 1∶2∶1, the time to reach the maximum plastic strain is the shortest and the probability of strain concentration at the region for handle is increased. When the thickness ratio is 1∶1∶2, the plastic strain of the tank body is relatively reduced, but the impact resistance does not reach the ideal optimized situation. When the thickness ratio is 1∶1∶2, the plastic strain is the smallest, the maximum instantaneous speed is the highest, and the property of the tank structure is the best. Based on these, a structural optimization idea is proposed. On the basis of adding a middle foam layer to reduce the weight, appropriately increasing the thickness of the outer polyethylene material or using a material with better cushioning performance can increase the buffer energy absorption of the tank wall and improve the strength of the material structure.
free drop; liquid storage tank; finite element simulation; mechanical response; equivalent plastic strain
TB485.1
A
1001-3563(2022)01-0066-09
10.19554/j.cnki.1001-3563.2022.01.009
2021-08-18
天津市应用基础与前沿技术研究计划重点项目(14JCZDJC34600)
张宇婷(1997—),女,天津商业大学硕士生,主攻无伞空投包装防护设计及有限元模拟。
计宏伟(1964—),男,天津商业大学教授、博导,主要研究方向为运输包装。

