构建物理模型 培养科学思维
——变质量气体问题解题策略探讨
(安徽省砀山中学,安徽 砀山 235300)
1 引言
物理建模是指在研究物体结构、物体相互作用、物体运动规律的过程中忽略次要因素,抓住主要因素,建立理想化物体模型、物理过程模型等,如质点、弹簧振子、人船模型、理想气体等都是高中物理中常见的物理模型。建构物理模型的过程是一个做“减法”的过程,忽略了次要因素,展现清晰、简明的物理情景,揭示隐藏在现象背后的规律。在“气体的性质”问题解决中,变质量气体问题的处理可以运用建模的方法进行处理与分析,从而方便地解决问题。
2 变质量气体问题的类型
2.1 气体散失
例1:一个开口的玻璃瓶,当瓶内空气温度由27℃升高到127℃时,瓶内剩下的空气质量是原来的几分之几?
模型建构:瓶内气体温度升高时,气体将从瓶口扩散到周围空气中去,可以假想在瓶口处套上一只塑料袋,收集从瓶内扩散的气体。将瓶内气体升温、塑料袋缓慢膨胀的过程视作一个等压膨胀的过程,建构“口袋”模型。
方法1:模型法
设玻璃瓶容积V1,气体升温平衡后玻璃瓶容积与塑料袋容积之和为V2。
研究对象:瓶内和塑料袋内的气体。
初态为:温度T1=300K、体积为V1,末态为:温度T2=400K、体积为V2。
方法2:运用理想气体状态方程等
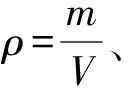
2.2 气体混合问题
例2:两个不同的容器中装有质量、温度均相同的同种气体,甲容器内气体压强为P1,乙容器中气体压强为P2,将两容器连通后,保持温度不变,求容器内气体的压强P。
模型建构:设甲容器容积为V1,乙容器容积为V2,且有V1>V2。由于两个不同的容器中装有质量、温度均相同的同种气体,则:P1 方法1:模型法 设乙容器气体膨胀了ΔV,则甲容器气体的体积被压缩为V1-ΔV,研究对象及状态参量如表1所示。 表1 方法2:运用道尔顿分压定律 混合气体的压强等于各组气体的分压强之和,用P表示混合气体的压强,P1、P2、P3……表示各组气体的分压强,P=P1+P2+P3+……。 从微观角度来看,理想气体的压强大小跟两个因素有关,一个是气体分子的平均动能,一个是气体分子的密集程度,而温度是气体分子的平均动能的标志。由于两容器是同种气体且质量和温度都相同,故气体分子数相同,设为N。 例3:一只两用活塞气筒,其筒内容积为V0,现将它与另一个容积为V的容器相连接。开始时气筒和容器内压强为P0,已知气体和容器导热性能良好。当分别用作打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器中气体压强分别是多少? 模型建构:充气时,将被充气体与容器内气体视为一个系统,缓慢充气过程为等温压缩过程。抽气时,将被抽气体与剩余气体视为一个系统,缓慢抽气过程为等温膨胀过程,然后将被抽气体再分割出去,从而可建构“整体”模型。 解析:(1)充气问题 方法1:分过程逐次分析 方法2:模型法 方法3:运用道尔顿分压定律 (2) 抽气问题 例4:一氧气瓶容积为0.08m3,开始时瓶中氧气压强为20atm。某实验室每天消耗1atm的氧气体积为0.36m3。当氧气瓶中的压强降低到2atm时,需要重新充气。若氧气的温度保持不变,求这瓶氧气重新充气前可供实验室使用的时间。 模型建构如图1所示,等温膨胀过程一为:20atm的氧气等温膨胀到2atm,等温膨胀过程二为:2atm的氧气等温膨胀到1atm。 图1 方法1:对于气体等温膨胀过程,气体状态及参量如表2所示。 表2 方法2:运用混合气体道尔顿分压定律有:P1V1=P2V1+NP3ΔV,代入数据得:N=4天。 例5:某容积为20L的氧气瓶装有30atm的氧气,现把氧气分装到容积为5L的小钢瓶中,使每个小钢瓶中的氧气压强为5atm,若每个小钢瓶中原有氧气压强为1atm,设分装过程中无漏气,且氧气温度不变,问:能分装多少瓶? 建构模型:运用混合气体道尔顿分压定律或气体密度公式结合质量守恒解决问题,建构相关物理模型。 方法1:运用道尔顿分压定律 设最多能分装n个小钢瓶,分装前气体状态P1=30atm,V1=20L,P2=1atm,V2=5nL;分装后气体状态P′=5atm,V′=(20+5n)L。据混合气体道尔顿分压定律有:P1V1+nP2V2=P′V′,代入数据解得:n=25瓶。 方法2:运用理想气体密度公式 物理问题解决的过程就是一个建模、推理、论证、质疑创新、提升思维能力的过程,为有效提高学生的科学思维能力,教师在教学中应精心设计问题,提高问题的科学性和有效性,在习题教学中注重一题多解、多题归一的训练,这样可有效培养学生思维的发散性、拓展性。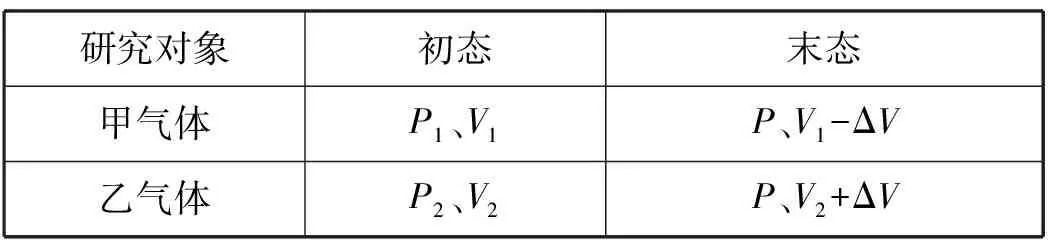

2.3 充气、抽气问题




2.4 漏气问题


2.5 灌气问题
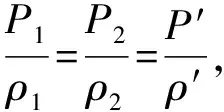
3 教学启示

