基于Boussinesq型方程的钱塘江涌潮数值模拟
黄婷,张怀,2*,石耀霖
1 中国科学院大学地球与行星科学学院,计算地球动力学重点实验室,北京 100049 2 南方海洋科学与工程广东省实验室 (珠海),广东珠海 519080
0 引言
涌潮是一种发生在涨潮期间的潮汐现象,来潮沿着河流或狭窄海湾逆流而上,形成波长和频率不断变换的潮波.涌潮的形成基于来潮、河流条件以及河道地形之间的微妙平衡,并非所有的河口都会发生涌潮.据估计,全世界发生涌潮的河口有四百多个,分布在除南极洲以外的所有大陆,河口附近的环境、生态以及文化都将受到涌潮所带来的影响(Chanson,2009).杭州湾是著名的涌潮地,而自澉浦以上的钱塘江出口段(图1)是世界闻名的强涌潮河口(谭维炎等,1995),因钱塘江河床泥沙易冲易淤,为治理钱塘江河口环境,20 世纪60 年代以来,治江缩窄工程不断推进(尤爱菊等,2010),河流边界内移,使得钱塘江河口处形成形态复杂多样的涌潮.最具代表性的潮景是大缺口的“交叉潮”、盐官的“一线潮”以及老盐仓的“回头潮”,每年都会吸引无数中外游客慕名而来,是我国独特的自然旅游资源.对钱塘江涌潮的研究,不仅具有学术意义,也具有重要的实际应用价值.

图1 钱塘江河口地形示意图黑色轮廓线是20世纪初钱塘江河流边界,蓝色线是江底地形等高线.Fig.1 Schematic diagram of the Qiantang EstuaryThe black outline indicates the boundary of the Qiantang River in the early 20th century.The blue line indicates the contour line of the topography of the river bottom.
几个世纪以来,国内外的学者一直致力研究涌潮现象.Saint-Venant(1871)对一维渠道内的水流进行观测,提出了著名的圣维南方程,并将其应用于法国塞纳河的涌潮,通过计算来潮的Froude数,判断涌潮的发生.一维模型基于理想假设,适用于流速方向易于评估,并且在整个涌潮持续时间内固定的河道(Clamond and Dutykh,2013).赵雪华(1985)应用一维圣维南方程,有机地结合特征线法和特征差分格式,计算了钱塘江自杭州闸口至下游澉浦之间河段涌潮时的水位和流量情况.于普兵和潘存鸿(2010)应用迎风格式有限体积法求解一维圣维南方程,建立了钱塘江涌潮一维数值模型,并模拟计算从上游富春江电站至下游澉浦河段的潮位情况.

钱塘江涌潮存在形状良好的波状涌潮和潮头破碎的强涌潮等多种形态,且波状涌潮的频散作用较大,需要在控制方程中添加频散项(潘存鸿等,2008),以往的模拟大多针对的是涌潮的传播过程并不考虑频散效应.综上所述,本文在前人研究的基础上建立了新的二维高阶Boussinesq型方程,采用有限体积法,考虑移动的干湿边界,对钱塘江涌潮进行数值模拟研究,探讨了在考虑频散作用下钱塘江涌潮的形成与传播特征.
1 模型与数值方法
1.1 控制方程
1.1.1 Boussinesq型方程
Madsen和Sørensen(1992)从经典Boussinesq 方程出发,提出了缓坡地形上的一种Boussinesq型方程,并通过理论分析和应用验证该方程比经典Boussinesq方程适用的水深范围更广.经典Boussinesq方程适用于水深与波长比值h0/λ0<1/5的水深区域,而Madsen和Sørensen的方程在调节适当的频散系数后可将应用水深扩展到h0/λ0<1/2的区域.Beji和Nadaoka(1996)同样从经典Boussinesq方程出发,通过对非线性项和频散项的数学关系代换,修正了Madsen和Sørensen的方程,提出了一种考虑地形变化的二维高阶Boussinesq型方程.我们在Beji和Nadaoka工作的基础上,导出在考虑河道弯曲变化和强烈地形起伏情形下不可压缩流体的二维高阶Boussinesq型方程,表示为
(1)
(2)

(3)
其中n为曼宁系数,F=F(fx,fy)为科氏力,有
fx=fv,fy=-fu,
(4)
其中f=2Ωsinφ为Coriolis参数,Ω为地球自转角速度,φ为纬度值.A=A(Ax,Ay)表示水平动量扩散
(5)
其中Am为水平涡流黏度系数,可以简单地采用涡流黏性去模拟湍流混合和波破碎时的能量耗散(Chen et al.,2000;Kennedy et al.,2000).B=(Bx,By)称为Boussinesq项或是频散项,是关于时间和空间的混合高阶导数,是在静水压力平衡基础上的一个附加项
(6)
其中h为静水深,参数β调节着方程的频散程度.
1.1.2 方程的线性频散性
长波假设意味着,波的特征振幅η0与特征水深h0相比较小,即系数ε=η0/h0≪1,波的传播体现为波的相位传播,且波的相速度与stokes一阶理论(即Airy线性波理论)表述的一致,于是可以在长波假设下对控制方程进行线性频散性分析.
线性频散关系表示为:
(7)
式中ω为波的频率,k=2π/λ为波数,h为静水深.进而得到波速c与水深的线性频散关系
(8)
将式(8)在kh=0处进行泰勒展开有
(9)
截取到O(k4h4)项,即方程的精度达到O(σ4)阶.
如前所述的控制方程(1)的频散关系表示为(Beji and Nadaoka,1996)
(10)
于是系统的相速度可以表示为
(11)



图2 非静水压力梯度的影响虚线表示初始波的形态,实线表示当前波的形态,空心箭头表示额外水平压力梯度方向.Fig.2 The influence of non-hydrostatic pressure gradientThe dashed line represents the shape of the initial wave,the solid line represents the shape of the current wave,and the hollow arrow represents the direction of the different horizontal pressure gradients.
1.2 数值方法
1.2.1 网格划分
在二维空间,采用节点中心格式设置空间交错的均匀网格,变量η、u和v分别在三套网格中进行求解,如图3所示.
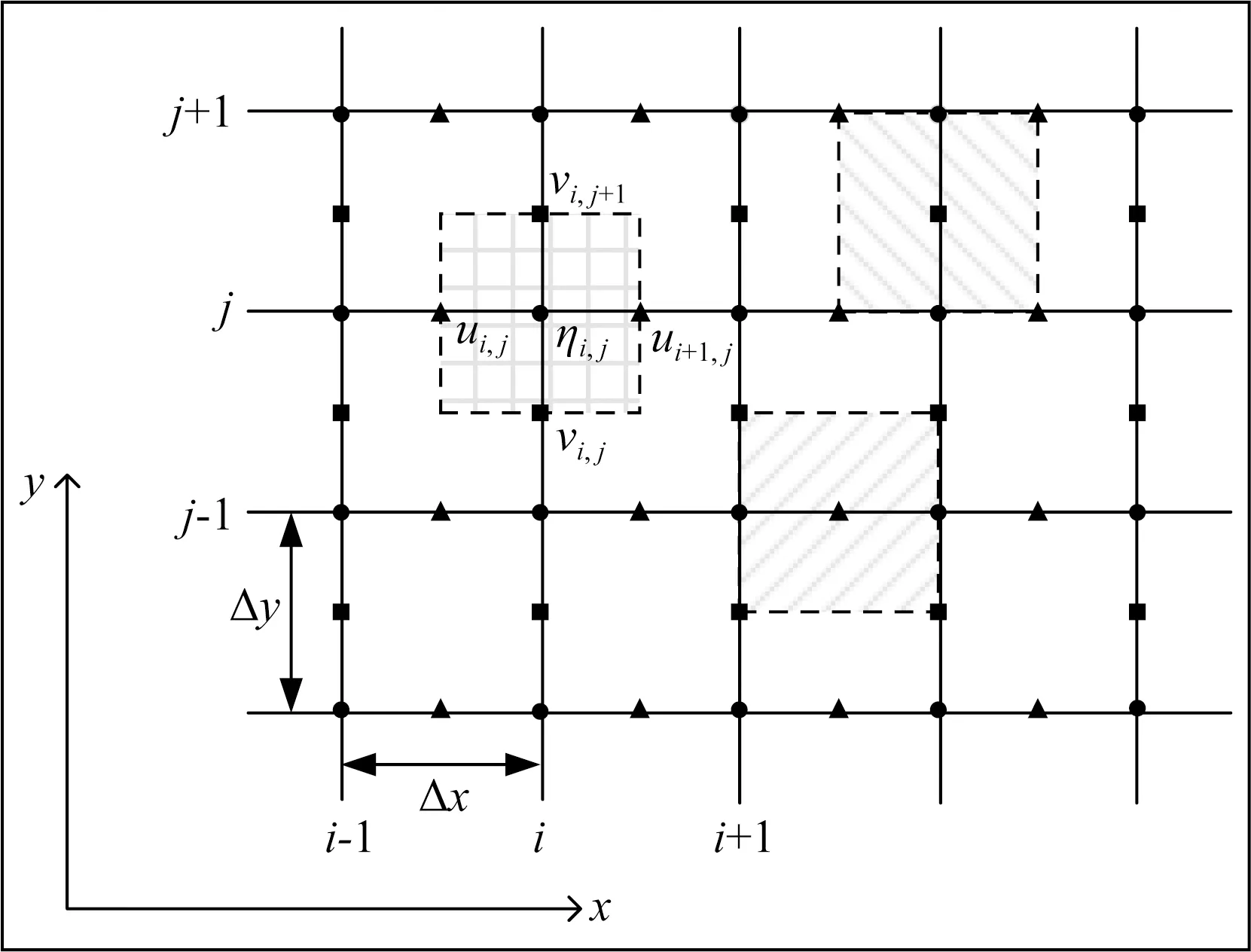
图3 交错网格节点与控制体积示意图三个物理量η,u和v所在计算节点分别表示为圆形、三角形和正方形,所在控制体积分别填充正交线、左斜杠和右斜杠表示.Fig.3 Schematic diagram of node and control volume of the computational gridThe nodes of three independent variables η,u,and v are expressed as circular,triangular,and square respectively.An orthogonal line,left slash,and right slash represents the corresponding control volume.
1.2.2 连续性方程
对连续性方程(1),在时间上采用向前欧拉格式,在空间上使用有限体积法.于ηi,j节点处,在以节点为中心的控制体积ΔVi,j内对连续性方程进行积分,引用高斯定理得
+Δx[(Dv)n-(Dv)s]=0,
(12)
式中S为控制体积ΔVi,j的外边界,n为边界S外法线的单位向量,下标e、w、n、s分别指示边界S的东、西、北、南四条边界.Δx和Δy分别为在x和y方向上的空间步长,控制体积ΔVi,j=Δx×Δy.边界处的水深使用相邻节点的水深平均值,得到
(13)
式中Δt为时间步长,k为当前时间步.
1.2.3 动量守恒方程

形如上述动量守恒方程的保守部分可以表示为关于变量φ的形式
(14)
式中ν为扩散系数.于φi,j节点处,在以节点为中心的控制体积ΔVi,j内对方程进行积分得到
(15)
再在时间上采用向前欧拉格式得到:

(16)
式中m为S的各个边界组分(e、w、n、s),Δm为边界长度,φm为边界处的变量值,整理后得
(17)
l表示边界处的切线方向单位向量.
对流项中C表示Courant数,展开有
上标“+”表示边界处速度方向与边界法线方向相同,上标“-”表示边界处速度方向与边界法线方向相反,即可以概括为
(19)
对于扩散项展开则有
(20)
对于控制体积边界处的值可以由其上下游处的节点值插值得到,如东边界处的值φe可以表示为如下形式:
(21)
式中函数Ψ称为通量限制器,与迎风侧的梯度与逆风侧的梯度比值r有关,r表示为
(22)
式中φu表示当前边界处的上游节点值,φu u表示φu的上游节点值,φd表示当前边界处的下游节点值,φd d表示φd的下游节点值,如图4所示.

图4 插值示意图黑色实心圆和空心圆分别表示节点位置和相应节点处物理量的值,黑色实心三角和空心三角分别表示边界位置和相对应的物理量的值.Fig.4 Schematic diagram of interpolationThe black solid circle and the hollow circle represent the position of the node and the value of the corresponding physical variables.The black solid triangle and the hollow triangle represent the position of the boundary and the value of the corresponding physical variables,respectively.
根据不同的使用需要,通量限制器函数Ψ具有不同的形式,最常被使用的格式见表1(Versteeg and Malalasekera,2007).

表1 常见的通量限制器函数表达形式(Versteeg and Malalasekera,2007)Table 1 Most popular limiter functions found in the literature (Versteeg and Malalasekera,2007)
Sweby(1984)根据r-Ψ关系给出了格式符合TVD方案的充要条件,还提出了对达到二阶以上高阶精度格式的要求.本文采用的QUICK格式可以保证TVD特性,且至少具有二阶精度.在均匀正交网格下,对于扩散项,使用TVD-QUICK格式有
(23)
于是得到方程保守部分的最终形式
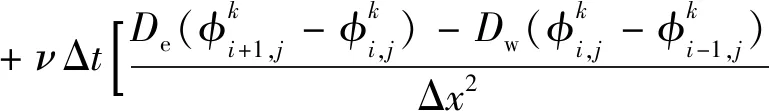
(24)
对于控制方程中的Boussinesq项在空间上采用有限差分法,我们将在算法测试中对一维方程的Boussinesq项进行具体离散.
1.2.4 稳定性分析
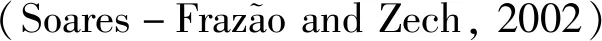
(25)

1.3 涌潮的生长

初始速度场分布与初始波形为
(26)
式中u0和a均为常数.
为简便操作,取初始静水深h=1,得到控制方程
(27)
η,u,x,t均为无量纲变换之后的变量,其中频散项有
(28)
对方程(27)使用数值格式中介绍的方法进行数值离散,将Boussinesq项离散之后得到

(29)
我们分别计算频散系数β=0和β=1/5的情况,并参照不考虑频散项的静水压力模型,测试中选择u0=0.1,dx=0.6,dt=0.25,a=6(Peregrine,1966),计算结果见图5.

图5 波状涌潮的生长过程.从下往上的曲线簇分别表示时间从0开始,以5增长直至20的计算结果灰色实线、红色实线分别表示使用Peregrine 1966年浅水模型和Boussinesq模型的数值计算结果,黑色虚线、黑色实线分别表示使用文中所述方程及算法在β=0和β=1/5时所得的计算结果.Fig.5 Growth of an undular bore.The curves from bottom to top represent the calculation results of time from 0 to 20 with 5 as the interval The gray solid lines and the red solid lines represent the computation results by Peregrine 1966 using the shallow water model and the Boussinesq model respectively,while the black dashed lines and the black solid lines represent the computation results using the equation and algorithm described above when β=0 and β=1/5 respectively.
从图5中可以看到,在模拟时间内,仅考虑静水压力的数值模型计算结果(灰色实线),波前缘逐渐变陡,但波后方仍旧保持平滑,波前缘涨幅保持在0.1;使用Boussinesq型方程的计算结果在初始一段时间内和静水压力理论的结果重合,而后波前缘逐渐隆起形成波峰,在波后方出现波谷,再现了波的频散(二次自由面起伏)特征,形成了波状涌潮.当频散系数β=0时,使用如前所述的算法计算结果(黑色虚线)与Peregrine 1966年的测试结果(红色实线)相当吻合,波前缘涨幅在0.15左右.而当频散系数β=1/5时考虑了更高阶的垂直压力分布改变对水平压力梯度变化的影响,因此计算得出的涨幅也会更大(黑色实线),波前缘涨幅在0.17左右.由测试结果可见,在涌潮模拟中对静水压力的校正是非常重要的,方程需要考虑频散项的影响.
1.4 模拟区域与初边值设置
海面的潮汐变化可以分解为许多简单的、规则的简谐振动,每个振动称为一个分潮,大多数地区的潮汐主要成分是由月球引起的主太阴半日潮.钱塘江河口潮汐现象即为一种半日潮.2000年,浙江省钱塘江管理局与浙江省河口海岸研究所对钱塘江河口进行了一次大规模考察性涌潮观测,钱塘江河口在地形上有两个显著的特点(林炳尧等,2002),一是杭州湾河口呈喇叭形;二是自乍浦往上至仓前、七堡之间,存在宏大的沙坎,其顶部比乍浦河床高出10 m左右.钱塘江潮波的变化、涌潮的形成和发展与这两种地形特点密切相关.澉浦是我国潮差最大的海域之一,但是当潮波通过杭州湾时,变形的程度并不明显,澉浦下游的潮位变化过程仍然接近简谐曲线.一般情况下涌潮自大缺口至盐官之间形成、发展,最终在七堡附近湮灭,大潮时期涌潮最远可到达杭州以上的闻家堰至富阳河段(Pan and Lu,2011).
根据实际涌潮的特点,我们的模型区域上游边界设置在闸口处,下游边界设置在乍浦下游,计算区域范围取值为120.15°E—121.25°E/30.0°N—30.7°N(图1),地形数据水平分辨率精度约90 m.河流东边界给定水面高度变化,使用与实际记录相近的正弦波形函数来模拟潮汐引起的强迫场(林炳尧等,2002),根据杭州湾的潮差分布(Fan et al.,2015)以及实测资料中的钱塘江涌潮的特性(林炳尧,2008),选择振幅amp=2 m,周期period=12 h.河流西边界在模拟的时间内假定为水深恒定速度自由,即水位边界条件为给定的恒定水深,速度边界设置为自由传输边界.模型考虑水波的上岸淹没情况,因此网格的干湿情况是时刻变化的,形成移动的干湿边界,网格干湿判断条件如下,取最小水深Dmin=0.01 m,即有
(30)
经各式模型的测试与实测校对表明,钱塘江河口底部的曼宁系数较小,约为0.01(潘存鸿等,2008),或者更小,取曼宁系数n=0.01,频散系数β=1/5,初始时间步长Δt=0.5 s.
2 模拟结果与分析
我们模拟了潮波进入钱塘江河口,上行直至上游闸口处,形成涌潮的整个发展过程.结果主要展示涌潮经过不同河段时的波高场以及速度场的变化,旨在从涌潮高度、涌潮传播速度、潮景等涌潮传播表征进行分析,探究在不同区域河段涌潮的特征.将陆地区域的名称,作为其所对应相邻的钱塘江河段的暂代名称,用于对涌潮经过此河段区域的定性分析.对钱塘江涌潮的观测资料显示,涌潮的形成基本在尖山一带,自大缺口至盐官河段发展达到最大,再往上行,涌潮高度逐渐减小,直至消失,其上界一般在七堡附近,最远也可到达杭州以上(谭维炎等,1995;林炳尧等,2002;潘存鸿等,2008).
因关注的重点在涌潮本身,我们将湿单元的数据进行提取并绘制成波高场图和速度场图.在我们的模型计算结果中,涌潮进入形成、发展和消亡三个阶段的位置和实际记录结果吻合.涌潮形成于尖山河段,该河段下游的水深在40 m左右,相对较深,此时的涌潮高度较小,潮头并不明显,潮波因江底沙洲和沿岸地形的影响分成两股波,在尖山和大缺口河段间形成“交叉潮”(图6a).随后涌潮从大缺口进入了较为平直狭窄的盐官甬道,大量水体涌入,表现出“一线潮”(图6b),且强度随着深入不断增大(图6c).在老盐仓拐角处,因转折角度较大,涌潮被反射形成“回头潮”(图6d).盐官上游之后的河段水深较浅,基本处于10 m以下,江底摩擦产生的能量耗散作用明显,再加上弯曲地形与涌潮之间的碰撞,涌潮强度开始减弱.涌潮后续经过几个拐角上溯至七堡河段(图6e),之后进入闸口河段走向消亡阶段(图6f).2.2小节将会对三处典型潮景的涌潮特征进行具体分析.
2.1 涌潮特征的沿程变化
涌潮高度、涌潮速度以及Froude数是表征涌潮特性的三个重要指标.涌潮高度ΔH一般指涌潮引起的平均水面上涨高度,ΔH=hd-hu,hu、hd分别表示涌潮潮头前方(即波前缘的上游方向)水深和潮头后方(即波前缘的下游方向)水深,如图7所示,相对涨幅表示为ΔH/hu.
使用涌潮潮头传播的速度描述涌潮速度,涌潮速度c的流量守恒方程和动量守恒方程可以表示为(以指向上游方向为流速的正方向)
c(hd-hu)=udhd-uuhu,
(31)
(32)
其中uu、ud分别表示潮前流速和潮后流速(图7).

图7 涌潮传播示意图uu、ud分别表示潮前流速和潮后流速,hu、hd表示潮前水深和潮后水深,c表示涌潮流速.Fig.7 Definition sketch of a bore propagationuu and ud are respectively the flow velocity before and after the tidal bore,hu and hd indicate the flow depths before and after the tidal bore respectively,c is the bore celerity.
由式(31)、(32)可以分别得到
(33)
(34)
联合整理式(33)、(34)之后得到由潮前、潮后流速表示的涌潮传播速度c为
(35)
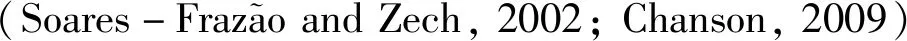
(36)
由式(36)可以看到,Froude数与潮前水深和潮后水深的比值相关,Fr越大,涌潮引起的前后水面涨幅落差也就越大.而c同时可以由Fr表示为
(37)
可见涌潮速度c与Froude数Fr、流速以及水深有关.我们选取靠近河道中心位置处的涌潮剖面,计算涌潮上述三个特征以及涨幅的沿程变化情况,具体计算结果见表 2.

表2 涌潮特征沿程变化Table 2 Variation of bore characteristics along the river

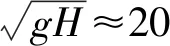
在不考虑老盐仓处的“回头潮”的情况下,我们将表中的数据按照钱塘江涌潮上溯的传播方向绘制了涌潮特征沿程变化,见图8.涌潮的Fr随ΔH自涌潮的形成阶段、发展阶段直至消亡阶段,整体呈现出先增大再减小的规律.自盐官以上河段的水深相差不大,在10 m左右,因此c也整体呈现先增大再减小的规律.涌潮于盐官河段处上溯,强度一直增大,于外五工段区域河道处规模达到最大,ΔH约为3.5 m,Fr约为1.54,c约为9 m·s-1,此时段的涌潮潮头陡立,自由表面可能失稳,波开始破碎.

图8 涌潮特征沿程变化曲线方块、三角、圆分别表示涌潮速度c、涌潮高度ΔH和涌潮的Froud数Fr.Fig.8 Curves of variation of bore characteristics along the riverThe celerity c,bore height ΔH,and Froude number Fr are expressed as square,triangular,and circular.
涌潮经过老盐仓处的急转弯,在反射和推挤作用下形成“回头潮”,“回头潮”的强度并不大,ΔH在0.7 m左右,Fr接近1.继续上溯的涌潮强度开始减弱但规模依旧较大,三工段至仓前的整个河段涌潮变化不大,ΔH约为2.5 m,Fr接近1.4,c约为8 m·s-1.在经过七堡至闸口河段,涌潮规模和强度都在减弱,Fr减小到近1.2,ΔH也仅有1 m左右,涌潮处在消亡阶段.闸口河段处的水深较七堡处要大,于是出现在闸口河段处的涌潮速度要稍微大于七堡河段处的涌潮速度,约为6 m·s-1.
从实测资料分析中发现,涌潮高度一般于盐官河段达到极值,最大可达3 m以上,涌潮传播速度在3~10 m·s-1之间,此后涌潮开始衰减,涌潮高度也逐渐减小,沿程的涌潮速度也呈现从小到大,再从大到小的变化规律,最大流速出现在盐官河段(林炳尧,2008;潘存鸿等,2008),可见我们的模拟结果和实际观测现象所得的特点是吻合的.
2.2 涌潮的发展与潮景的形成
潮景的形成是涌潮不同发展阶段的标志,我们复演并选取了最具代表性的三个河段位置处的潮景,分别是大缺口处的“交叉潮”,盐官处的“一线潮”以及老盐仓处的“回头潮”.
2.2.1 交叉潮
尖山河段是钱塘江河口的一个转折处,河口近似呈“之”字形,从此处潮波由较为深广的水域经大缺口进入浅窄且平直的盐官河段.大缺口附近河口呈平躺的“U”字形,因泥沙淤积,钱塘江河口下游发育一巨大江中沙洲(图1),在大缺口下方尖山河段分汊河势以及江中沙洲的影响下,此处常常发育“交叉潮”(潘存鸿等,2008).
潮波在通过沙洲时被分成了两股波,一股沿着北岸向西北传播,另一股沿着南岸向西南方向传播(图9a),潮波带来整个尖山河段水面的上涨,并未形成明显的涌潮现象.两股暗潮相互作用,使得西北向潮波得到加强,于尖山河段下游形成较为清晰整齐的波,涌潮形成(图9b),涌潮的方向指向河流的上游.事实上,涌潮的形成并不是瞬时的,而是一个连续的过程,因此无法具体准确地判断涌潮形成的精确位置与时间,当肉眼可分辨涌潮形态时,我们即认为涌潮形成.在模拟时间的80 min左右,从图9c的涌潮剖面中可以看到,尖山河段潮头涨幅可以达到1.5 m,涌潮高度仅约0.3 m,计算出Froude数在1左右,涌潮形成初期波形平缓,波列整齐.
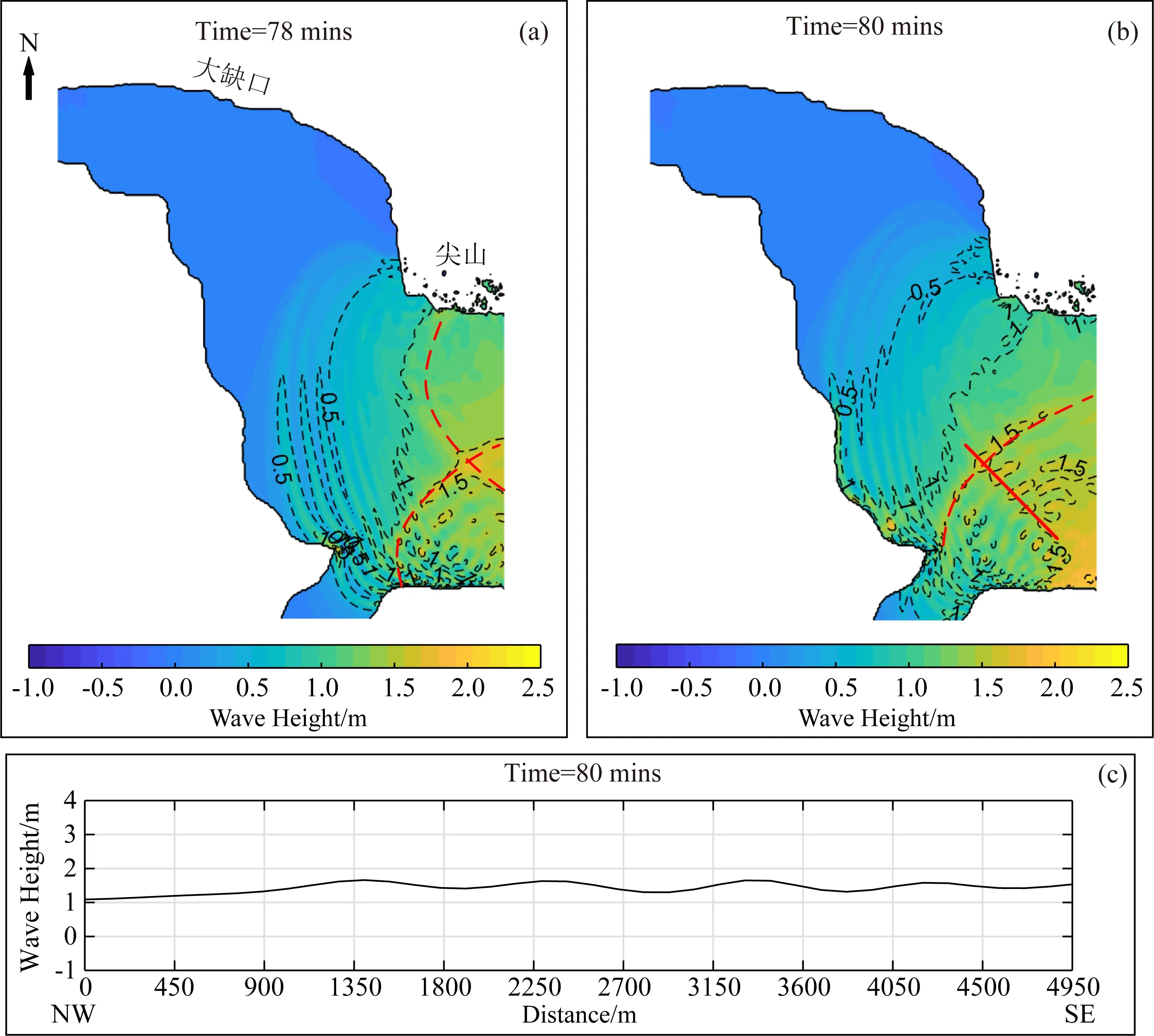
图9 尖山河段涌潮图(a—b)展示了不同时刻潮波引起的尖山河段的水面变化.红色虚线表示涌潮的波前缘,红色实线表示截取的涌潮剖面.图(c)展示了图(b)中的涌潮西北-东南方向的剖面形态.Fig.9 Tidal bore in JianshanFigures (a—b)show the variation of water surface at Jianshan at different times respectively.The red dashed line indicates the wavefront of the tidal bore wave,and the red solid line indicates the selected tidal bore profile.Figure (c)shows the bore profile in figure (b)from NW to SE.
在波状涌潮上溯的过程中于尖山至大缺口河段形成“交叉潮”(图10).尖山至大缺口河段是一个近似由西向北的转弯,在潮波与南岸边发生反射推挤作用的影响下,南岸形成了一股近似由南向北传播的涌潮(图10a),另一股涌潮沿着东南向西北行进,两股涌潮的潮头波高皆约为1.5 m,两股波前形成一个钝角的“人”字形.此时涌潮高度较小,波形完好,显示出良好的波的特征.两股涌潮继续上行,进入大缺口河段入口,两组波列相互干涉,波前形成了一个近似交叉的“十”字,即所谓的“交叉潮”(图10b),波前缘的夹角依然是钝角.在“交叉潮”后方清晰可见由干涉产生交错排列的明暗纹,波峰处涨幅在1.5 m左右,波谷处涨幅在1~1.5 m之间,波后的水面上涨约为2 m.“交叉潮”向大缺口行进,波前缘夹角逐渐减小(图10c),向北传播的涌潮接近北岸,涌潮的形态也重新呈现“人”字形.

图10 “交叉潮”波高场图(a—d)展示了不同时刻尖山河段的水面变化,红色虚线表示涌潮的波前缘,涌潮从尖山河段上溯至大缺口河段的过程中形成“交叉潮”.Fig.10 Wave height field of cross-shaped tidal boreFigures (a—d)show the variation of water surface at Jianshan at different times respectively.The red dashed line indicates the wavefront of the tidal bore wave.The cross-shape tidal bore is formed when the bore goes upstream from Jianshan to Daquekou.
“交叉潮”形成时,涌潮波的传播速度虽然接近20 m·s-1,但流场的速度较小,约为1 m·s-1,波的传播速度比流体速度大得多.速度方向的分布和两股潮的行进方向一致,波峰的位置处流场速度较大,而波谷位置处的流场速度较小,流场也呈现出与波场类似的明暗条纹分布,如图11所示.

图11 “交叉潮”速度场箭头方向表示速度方向,箭头长度表示速度大小,红色虚线表示涌潮的波前缘位置,速度场因速度方向和大小的变化呈现出与波纹类似的明暗条纹.Fig.11 Velocity field of crossed tidal boreThe direction of the arrow indicates the direction of velocity while the magnitude indicates the strength,and the red dashed line indicates thewavefront of the tidal bore wave.Due to the variation of strength and direction,the velocity field presents light and dark fringes.
2.2.2 一线潮
盐官以上的上游河段水深较浅,在10 m以下,因此涌潮在进入浅窄且平直的盐官河段后,水面高度迅速上涨,潮头走向几乎垂直于岸边,且波列以近乎平行的姿态上溯,于盐官河段附近形成较为理想的“一线潮”潮景(图12).“一线潮”是涌潮的发展阶段,涌潮强度开始增大.盐官河段处形成强度较大的“一线潮”,涌潮高度约为3 m.之后“一线潮”保持着相似的形态,强度继续变大,通过整个盐官河段到达外五工段河道区域.
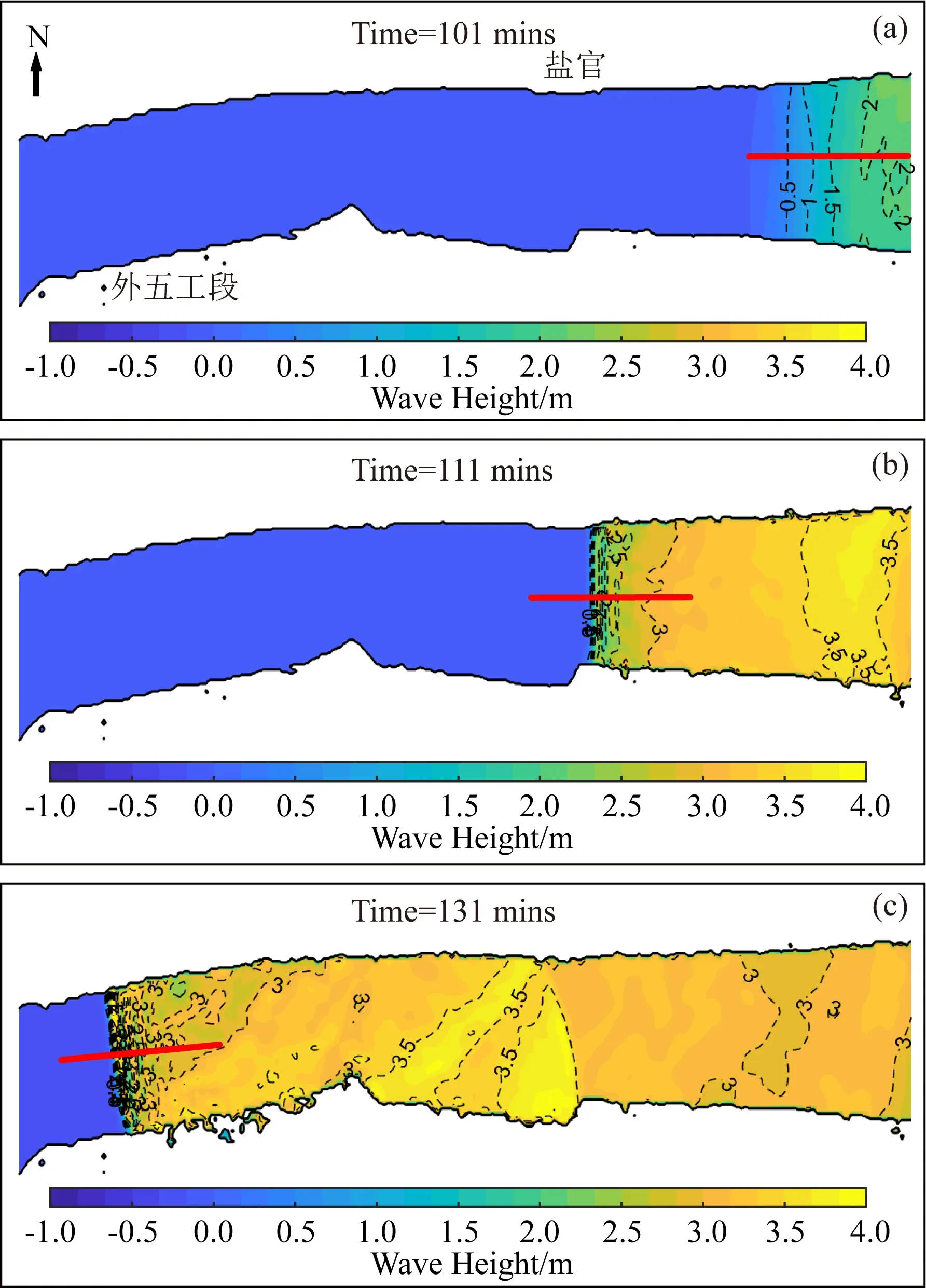
图12 “一线潮”波高场图(a—c)展示了不同时刻潮波引起的盐官河段的水面变化,涌潮通过盐官河段时,潮头处波高等值线变密,潮头急速抬升,形成“一线潮”,红线表示截取的涌潮剖面.Fig.12 Wave height field of thread-shape tidal boreFigures (a—c)show the variation of water surface at Yanguan at different times respectively.When the tidal bore reaches the Yanguan outlet,the wave height contour at the bore head becomes denser and the bore head rises steeply,then the thread-shape tidal bore forms.The red line indicates the selected tidal bore profile.
从波形剖面可以清楚地看到涌潮强度不断增大的过程.涌潮在进入盐官河道入口时,依然可见波前缘后方一系列形态良好的波(图13a).较为平缓的波前缘成长为陡立的潮头,且潮头前的水面会出现略微下降,在盐官处形成明显的间断面(图13b),计算得到涌潮的Froude数约为1.45.直至在盐官河段的出口处,外五工段的附近,涌潮的潮头一直在上涨,达到将近4 m(图13c),Froude数达到1.54.

图13 “一线潮”涌潮剖面展示了图12中选取的涌潮剖面,涌潮自东向西通过盐官河段,潮头逐渐陡立,涌潮强度增强,二次面起伏现象明显,具有强频散作用.Fig.13 Profile of thread-shape tidal boreThis figure shows the tidal bore profile selected in Fig.12.The tidal bore passes through the Yanguan outlet from east to west,the tidal head becomes steep,the intensity of the tidal bore increases,secondary free-surface undulations are reproduced,and the bore has a strong dispersion effect
涌潮经过盐官河段的速度场分布近乎与岸边平行,涌潮的波前缘存在明显的速度分界.在盐官河段入口附近,两股流场交汇处的速度相近,速度大小约为1 m·s-1,波前缘处流体速度接近为零(图14a).随着涌潮深入,潮波进入甬道,潮后速度逐渐增大,于盐官处形成“一线潮”时潮后的下游流场速度约为3 m·s-1(图14b).“一线潮”上溯速度继续增大,盐官河段的出口处连接老盐仓拐角,因此在外五工段附近,南岸的速度略微大于北岸(图14c),靠近南岸的流场速度在3 m·s-1左右.经计算的盐官河段涌潮速度在6~9 m·s-1,与流体速度仅相差几倍,可见涌潮已不再是简单的浅水模式,具有很强的频散效应.

图14 “一线潮”速度场图(a—c)展示了不同时刻盐官河段的速度分布,箭头方向表示速度方向,箭头长度表示速度大小,红色虚线表示涌潮的波前缘位置.Fig.14 Velocity field of thread-shape boreFigures (a—c)show the velocity distribution at Yanguan at different times respectively.The direction of the arrow indicates the direction of velocity while the magnitude indicates the strength. The red dashed line indicates the wavefront of the tidal bore wave.
2.2.3 回头潮
老盐仓拐角处夹角接近130°,“一线潮”于拐角处发生反射,在老盐仓形成了“回头潮”的潮景.弯道处造成的碰撞和反射使得涌潮波与岸边作用加强,且较浅的水深使得江底摩擦作用显著,涌潮能量被耗散,于是在“回头潮”出现之后,涌潮强度开始减弱.涌潮发生反射时,整个流场由下游来潮、反射波以及上游河流三个部分的流场组成(图15b),外拐角处水面上涨最大可达4 m.沿着河道上行的涌潮叠加部分反射波继续上溯,进入三工段区域河道.三工段河道与盐官河段相似,狭长且河面宽度较为均匀,涌潮进入河道后,以“一线潮”的形态前进,其规模较盐官河段的“一线潮”要小,涌潮强度开始减弱,涌潮高度减小到约为2 m(图15c).反向往下游传播的 “回头潮”,潮头涨幅在3 m左右,涌潮高度约为0.7 m(图15d).涌潮经过老盐仓所带来的水面上涨在3 m左右,老盐仓内拐角内侧岸边处的一些洼地被水填满.“回头潮”发生后,上溯涌潮的强度开始减弱,在经过七堡河段的拐角之后,涌潮进入消亡阶段.

图15 “回头潮”波高场图(a—d)展示了不同时刻潮波引起的老盐仓河段的水面变化,红色虚线表示涌潮的波前缘,涌潮在老盐仓处发生反射,形成自西向东传播的“回头潮”.Fig.15 Wave height field of returned tidal boreFigures (a—d)show the variation of water surface at Laoyancang at different times respectively.The red dashed line indicates the wavefront of the tidal bore wave.The tidal bore is reflected at Laoyancang,returned tidal bore forms and spreads from west to east.
老盐仓拐角处,上下两股流场交汇,速度场的分布情况和波高场分布相似(图16),由来潮、上游河流以及反射波三个速度场组成,涌潮的波前缘存在明显的速度分界.反射波的速度方向仍然是总体指向上游的,拐角处的速度最小,仅在1 m·s-1左右(图16b).指向上游的老盐仓反射波和上溯的涌潮相叠加,以约为3 m·s-1的速度进入三工段区域河道,与上游的速度流场的交界处呈“一”字形态(图16c).部分反射波形成“回头潮”反向向东传播,减慢了上溯流场的速度,“回头潮”的强度也不断减弱,涌潮同样具有很强的频散效应.
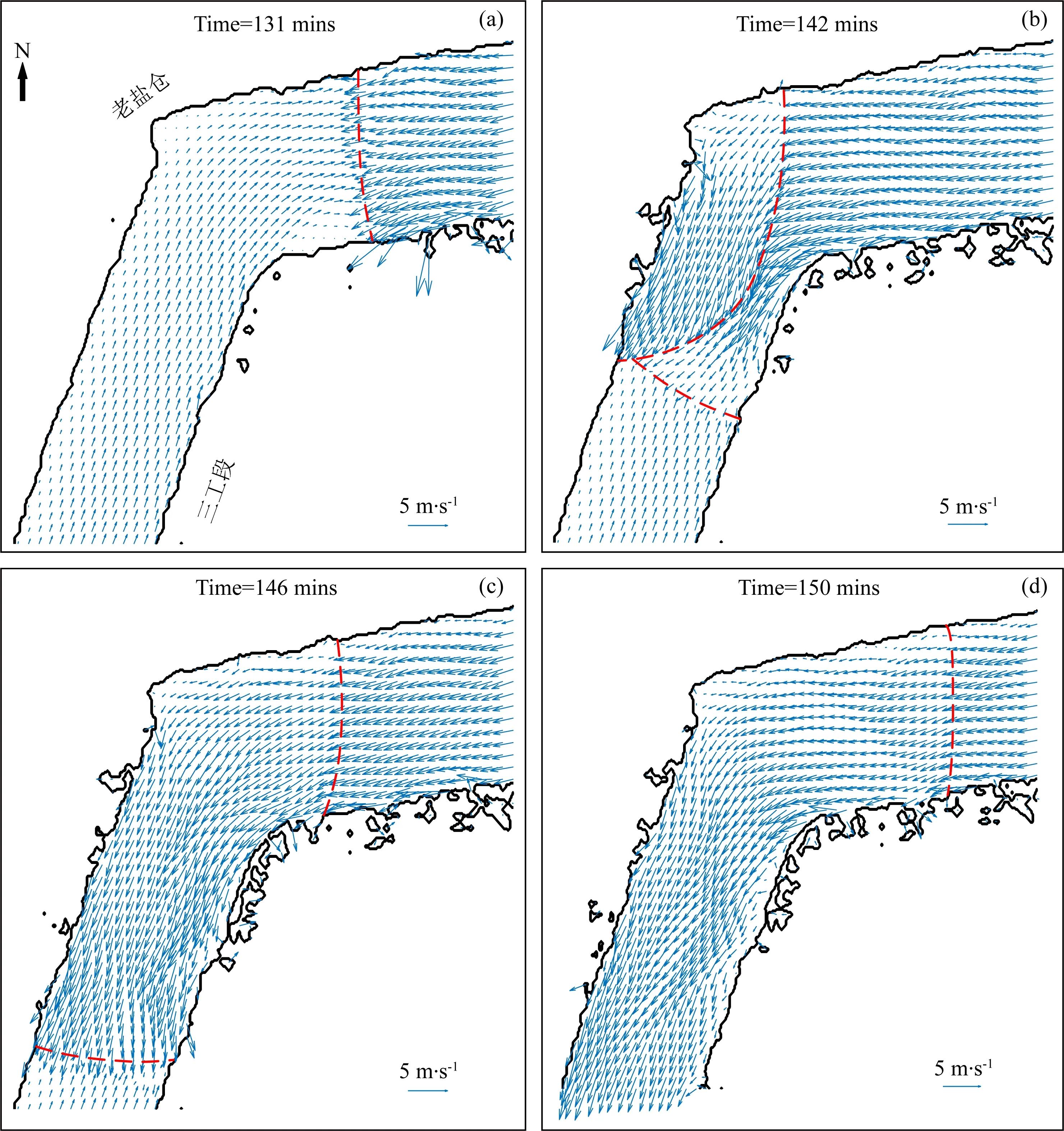
图16 “回头潮”速度场图(a—d)展示了不同时刻老盐仓河段的水流速度分布,箭头方向表示速度方向,箭头长度表示速度大小,红色虚线表示涌潮的波前缘位置.Fig.16 Velocity field of the returned tidal boreFigures (a—d)show the velocity distribution at Laoyancang at different times respectively.The direction of the arrow indicates the direction of velocity while the magnitude indicates the strength.The red dashed line indicates the wavefront of the tidal bore wave.
3 结论与展望
通过对钱塘江河口涌潮的数值模拟研究,我们得到以下结论:
(1)钱塘江河口涌潮的形成和发展以及潮景的产生和钱塘江的地形特征密切相关,模拟结果与实际观测中得到的结果可以很好吻合.潮波自钱塘江河口经过江底沙洲的作用以及与江岸间的相互作用,在尖山至大缺口河段发育形成“交叉潮”;在盐官河段,地形较为平坦,两岸长直且近似平行,涌潮由较为深广的水域进入浅窄的甬道时,波列逐渐均匀,形成“一线潮”;在老盐仓拐角处,涌潮发生反射,形成“回头潮”;“一线潮”潮景不仅发生在盐官河段,三工段附近也出现了波动形态良好的波状涌潮,同样呈“一”字形.
(2)本次模拟复演了最具代表性的“交叉潮”、“一线潮”以及“回头潮”三大潮景,盐官河段“一线潮”表现的频散效应最强.潮景的形成标志着涌潮进入不同发展阶段,“交叉潮”出现在涌潮初期,Froude数接近1,涌潮高度在0.5 m左右;涌潮由大缺口进入盐官河段之后形成“一线潮”,进入涌潮发展阶段,并达到最大规模,“一线潮”的Froude保持在1.45以上,涌潮高度最大可达3 m,且涌潮的频散作用较强;随后涌潮到达老盐仓形成“回头潮”,同时涌潮强度被减弱,继续上溯的涌潮进入三工段河道区域形成规模较小的“一线潮”,Froude数在1.3~1.4之间,涌潮高度约为2 m;七堡之后,上溯的涌潮进入消亡阶段,Froude数减小至1.3以下,涌潮高度约为1 m.
(3)钱塘江涌潮过程中,Froude数和涌潮高度呈正相关,涌潮形成至进入消亡阶段,Froude数随涌潮高度呈现逐渐增大再逐渐减小的规律.尖山河段处涌潮Froude数接近1,盐官河段涌潮的Froude数最大可达1.54,老盐仓之后,涌潮的Froude数逐渐减小.
(4)Boussinesq型方程可以很好地再现钱塘江河口涌潮的形成、发展和消亡阶段,对于盐官河段处这类具有较强频散效应的涌潮,展现了涌潮中的二次自由面起伏现象.
我们在前人工作的基础上,进一步发展了钱塘江涌潮数值模型,使用考虑非线性、频散以及耗散作用的Boussinesq型方程对钱塘江河口涌潮进行模拟,模拟结果与实际观测中体现的特征相吻合.
在后续的工作中,考虑使用Boussinesq型方程结合更高精度的地形数据以及实时的涌潮观测资料,可以运用在巩固堤防、维护河道、保护涌潮等数值模拟方面的工作,推进日后对钱塘江涌潮的保护和深入研究探索.同时在强烈风暴作用下,风浪过程对水位的影响也十分重要(张舒羽和潘存鸿,2013;Luettich and Westerink,2015),进一步工作中可以在本文使用的数值模式基础上考虑风浪与潮流的相互作用,增强涌潮防灾减灾的实用性价值.
致谢感谢中国科学院大学计算地球动力学重点实验室提供的计算平台.

