基于ARIMA 的城市交叉路口交通流预测建模
徐翠翠
(陕西交通职业技术学院基础学科部,陕西西安 710018)
伴随着城市规模的迅速发展、道路网络的不断完善及汽车保有量的迅速增加,交通问题已经成为城市发展和管理的重要问题之一[1]。公路容量与交通总需求的差距越来越大,交通供需矛盾日益突出[2]。虽然很多城市都建立了城市轨道交通系统,但乘客在早晚高峰期间的拥挤状况仍令人十分担忧。传统的交通预测统计方法主要有历史平均模型和数理统计理论[3]。尽管历史平均模型能在一定程度上解决不同时期交通流量变化的问题,但是静态预测方法存在着固有的缺陷。利用数理统计理论进行预测的方法比较简单,但其缺点是基于线性基础[4]。随着预测区间变小,交通流变化的随机性、非线性增强,模型性能变差。因此,提出了基于ARIMA 的城市交通流量预测方法。ARIMA 模型是时间序列建模的一种方法,ARIMA 模型的基本思想是将非平稳时间序列经过多个差值转换成平稳时间序列,再根据差值确定城市交叉口的交通流量。
1 交通流预测建模原理
针对城市交叉口时间随机性,提出了基于ARIMA的交叉口交通流预测模型。交通流量预测建模原理如图1 所示[5]。
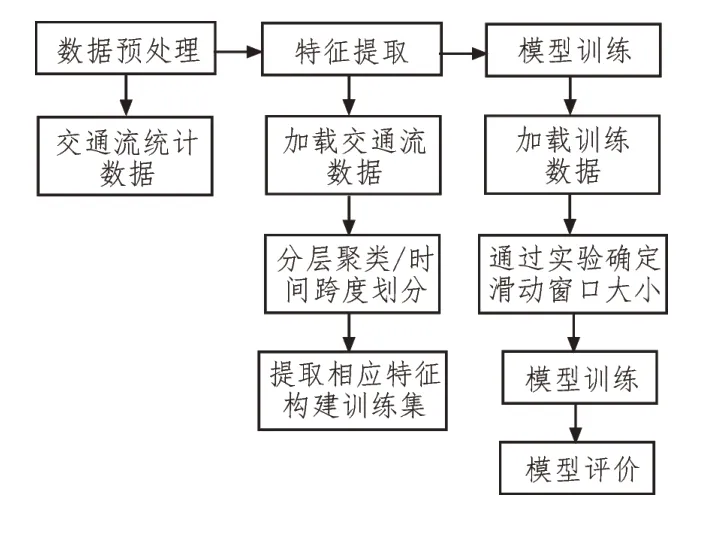
图1 交通流预测建模原理
模型分为如下3 个步骤:
第一步:数据预处理。由于原始数据信息复杂庞大,需要对其进行筛选提取,并对每天或每月的客流分布特征进行可视化分析;
第二步:特征提取。游客流量具有明显的潮流特征。游客流量的差异不仅表现在高峰时段,还表现在工作日和周末。为发现周期差异,首先对提取的数据进行聚类,识别周期差异,与此同时,可以降低数据维度,最终确定时间间隔,并选择客流特征明显的站点作为研究对象;
第三步:模型训练。在处理后,滑动窗口的大小会决定数据集中的数据[6]。滑动窗是指由前n个周期的数据预测当前的数据,视窗尺寸是每个输入资料的尺寸,不同的视窗尺寸会直接影响最终的预测结果,因此需要选择合适的视窗尺寸[7]。在此基础上,确定算法的参数,建立适合的客流预测模型,并利用不同的评价指标对模型进行评价[8-10]。
2 基于ARIMA交通流预测建模流程
2.1 不同时间序列交通流特征
从城市路网来看,交通拥挤的原因多发生在交叉口。作为城市道路交通的瓶颈,交叉口交通流的特点具有一定的代表性[11]。文中对不同时间尺度交叉口的交通流特征进行了分析,为了方便描述,以主干道段(西行单向段)为主要研究对象[12]。
设时间序列的平均相关系数为θ,该系数以d为单位,确定每k个交通量时间序列数据,作为一个列向量fi,并选择所有数据向量构成矩阵,如式(1)所示:
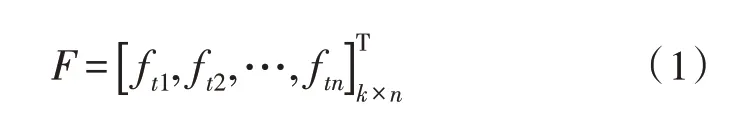
计算该矩阵的平均相关系数,如式(2)所示:

式(2)中,R为向量矩阵的相关系数矩阵;R(i,j)表示两个数据向量间的协方差[13]。
提取现场每天24 h 交通流数据,从2019 年7 月8号到8 月4 号共28 天的数据作为研究对象[14-15]。分别以5 min、10 min、15 min 和45 min 为时间序列,选择4 个周期组成相关矩阵,并计算矩阵平均相似系数,对比结果如表1 所示。
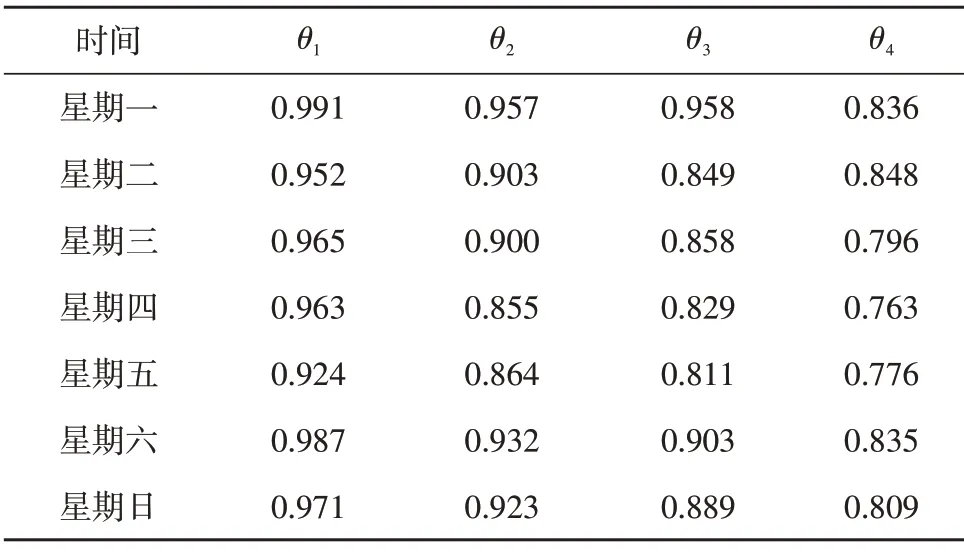
表1 平均相关系数
由表1 可知,随着时间缩短,时间序列相关性减弱[16]。短序列交通流流量数据相关性较弱,数据分布离散性强。
2.2 时间序列预测误差控制
该模型是一种随机时间序列模型,能识别出时间序列的结构,并通过协方差矩阵极小化来求得最佳预测值。设时间序列为Xt,函数由相邻数据和随机项决定,如式(3)所示:
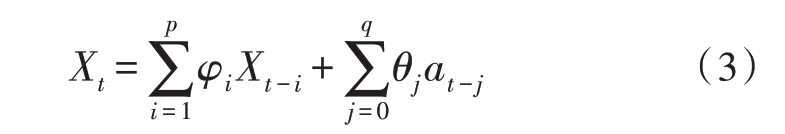
式(3)中,p、q均表示ARMA 模型阶数;at-j表示随机误差项;φi、θj分别表示模型自回归参数和平均系数,如式(4)、式(5)所示:
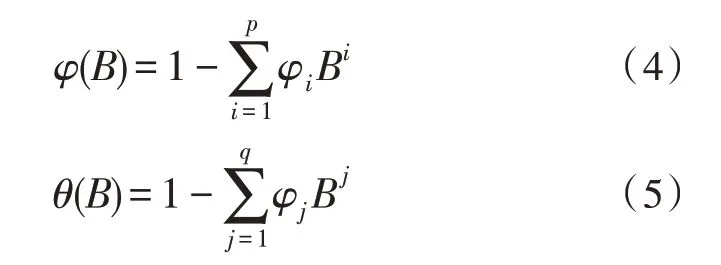
式(4)、式(5)中的B表示滞后算子。
如果时间序列残差表现出一定差异性,那么为了处理时间序列的异方差性,需要对残差进行分析。对残差下的非平稳时间序列进行预测,如式(6)所示:

式(6)中,d表示平稳化过程差分阶段。
ARRIMA 阶数是通过自相关系数和单位根来估计和检验的,阶数q和P是通过自相关系数和偏自相关系数来确定的。偏自相关系数描述了当前时间序列和不含中间变量的历史经验时间之间的关联,也就是在一个时间序列中不存在中间变量。
为了更好地描述时间序列的分布特征,假设误差项εt,一般误差分布的概率密度函数为随机变量值,数值为常数,因此可以设定期望为0,方差为1,其形式如式(7)、式(8)所示:
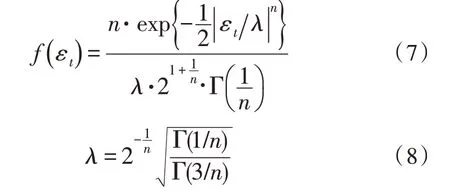
式(7)、(8)中,Γ(·)表示伽马函数;n表示时间序列分布重复特征参数;εt表示标准正态分布;当n≥2 时,标准正态分布比正态重复特征参数多。当n<2 时,标准正态分布比正态重复特征参数少,说明误差小。
2.3 交通流预测建模
根据上述误差控制,设存在n个hi(t)时间序列正常客流量,该交通量实时预测模型为:
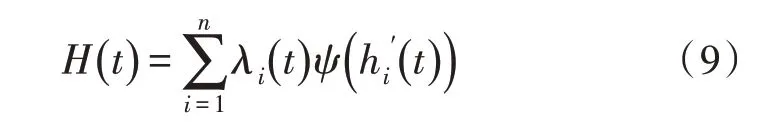
如图2 所示,在简明信息的支持下,不断深入分析交通大数据。对有关的重要数据进行分析,对生产操作进行优化指导,为用户提供新的信息需求,持续改进和更新系统结构、业务模块和功能域,为城市交通管理提供更加实时准确的信息。

图2 交通流预测实现流程
以约简信息的属性为基础,采用状态转移方程和观测方程来估计离散控制系统的实际状态,并用连续测量信息来修正预测值。用ARIMA 建立交通流预测模型,如图3 所示。
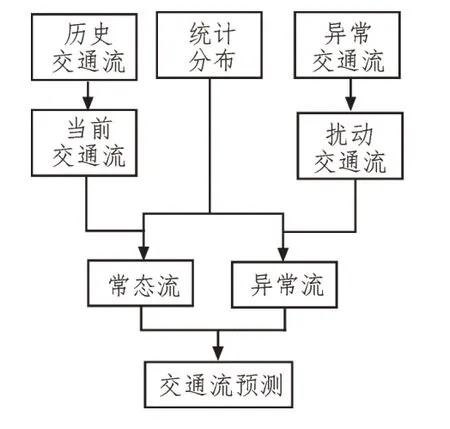
图3 交通流预测模型
由图3可知,对于历史交通流、当前交通流的时序特征、环境变化数据、常规交通流、干扰交通流、正常交通流和异常交通流,所构建的预测模型充分考虑了上述因素,对各条件值进行过滤和量化,生成二维决策表。然后,对属性约简结果进行再组合,作为训练样本输入模型进行学习训练,由此完成交通流预测。
3 实 验
3.1 实验环境
到2018 年底,A 市围绕景区开通了16 条地铁线路,其中地铁站点413 个,运营里程676 km。尽管每天的客流在一千万人次以上,但是节假日的客流却比平时多3~4 倍。服务时间大多在早上5 点到晚上11 点之间。当客流超过最大流量时,交叉口将采取相应的交通控制措施。
3.2 实验结果与分析
分别使用历史平均模型、基于数理统计理论方法和基于ARIMA 预测建模方法对交通早高峰和晚高峰时段交通流预测精准度进行对比分析,结果如图4 所示。

图4 不同方法早高峰和晚高峰时段交通流预测精准度对比
由图4(a)可知,使用历史平均模型预测交通流最高值为760 pcu/h,最低值为398 pcu/h;使用基于数理统计理论方法最高值为910 pcu/h,最低值为250 pcu/h;使用基于ARIMA 预测建模方法最高值为950 pcu/h,最低值为310 pcu/h,与实际值一致。
由图4(b)可知,使用历史平均模型预测交通流最高值为680 pcu/h,最低值为198 pcu/h;使用基于数理统计理论方法最高值为880 pcu/h,最低值为100 pcu/h;使用基于ARIMA 预测建模方法最高值为520 pcu/h,最低值为270 pcu/h,与实际值一致。
4 结束语
针对城市交通列车调度问题,提出了基于ARIMA 的城市交叉路口交通流预测建模方法,使用时间序列方法构建模型,该方法计算简单、预测精度可靠,适合城市交叉口信号控制,是一种值得推广的短时交通流量预测方法。

