基于水化进程的硬化水泥浆体电导率动态计算模型

何 丽，陈 庆，蒋正武，*

（1.同济大学材料科学与工程学院，上海 201804；2.同济大学 先进土木工程材料教育部重点实验室，上海 201804）

水泥基材料的电导率受孔隙率、孔隙溶液饱和度、孔隙溶液电导率等多因素的影响［1-9］.国内外学者提出了许多电导率模型［10-12］，如：Neithalath等［8，13］基于非均相混合物导电特性与单个组分导电特性，建立了非均匀混合物导电特性的Hanai-Bruggeman方程；Liang等［10］根据水泥基材料的孔径分布，建立了水泥基材料的电导率模型.这些模型尽管考虑了多种因素对水泥基材料电导率的影响，但孔隙溶液离子浓度和孔隙率是动态演变的，与此相关的孔隙溶液电导率和硬化水泥浆体电导率亦是时变的［14-16］.现有电导率模型鲜有考虑溶液电导率和水泥基体电导率的时变性，在评价水泥基材料电学性能的动态演变过程方面有一定的局限性.

本文基于水泥水化进程，利用水化动力学、质量守恒定律和电解质溶液导电理论，建立硬化水泥浆体电导率的动态计算模型.该模型能反应水泥水化过程中孔隙溶液离子浓度、孔隙溶液电导率、孔隙率以及硬化水泥浆体电导率的动态变化，同时也能指导水泥基材料电学性能调控设计，为水泥材料的电测技术提供理论基础.

1 基于水化进程的硬化水泥浆体电导率模型

1.1 硬化水泥浆体电导率基本模型

水泥水化过程中会发生可溶性盐溶解和硅酸盐水化2种反应，均会导致水中出现大量游离的导电离子，如Na+、K+、OH－、、Ca2+等，同时生成大量水化硅酸钙（C-S-H）凝胶等水化产物，且随着水化反应的持续进行，水泥浆体逐渐失去可塑性，并最终形成由水化产物、孔隙溶液和空气组成的三相复合硬化水泥浆体结构［17-18］.

复合材料电导率理论认为硬化水泥浆体的电导率σt是由固相、液相、气相电导率组成，其计算式［11，19-20］为：

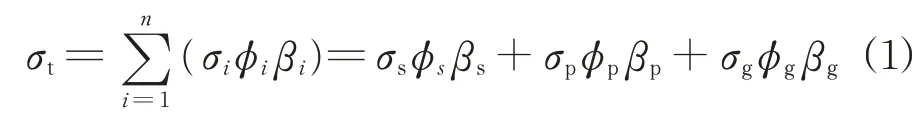
式中：n为硬化水泥浆体的组成相数；σi、ϕi、βi分别为第i相的电导率、孔隙率、连通性系数；下标s、p、g分别表示固相、液相、气相.

Rajabipour［19］研究表明，水泥基材料的液相电导率为1～20 S/m，固相和气相电导率分别为10－9、10－15S/m.由于固相和气相电导率远小于液相电导率，因此可近似忽略固相和气相电导率对硬化水泥浆体电导率的影响，从而得到σt＝σp［19］.

硬化水泥浆体的电导率由其孔隙溶液的电导率和孔隙率决定，而孔隙溶液的电导率和孔隙率都与水泥水化息息相关［16］.根据电解质导电理论，孔隙溶液电导率σp可表示为每种离子等效电导率的加权和［21］：

式中：zi为离子的价态；ci为离子浓度，mol/L；λi为离子等效电导率，S·m2/mol.

由式（2）可知，孔隙溶液电导率与离子种类和浓度相关.水泥水化反应过程中产生的离子会受到水泥化学组分、水化程度、水胶比（mw/mB）的影响.史才军等［22］研究表明，水化后期水泥浆体孔隙溶液主要是由K+、Na+、OH－和组成，Ca2+可忽略不计，其中浓度可以通过K+、Na+的浓度（c（K+）、c（Na+））进行估算［23］：

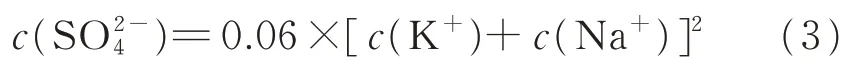
由电荷守恒可知OH－的离子浓度c（OH－）为［23］：

综上，可得水化后期硬化水泥浆体的电导率σt为：

式中：λ（K+）、λ（Na+）、、λ（OH－）分别为K+、Na+、、OH－的等效电导率.

忽略溶质对溶液体积的影响，孔隙溶液的孔隙率ϕp与水胶比、水化程度相关［24］；离子等效电导率λ与离子浓度有关；离子浓度与材料的组成和水化程度相关［16］.因此，基于水泥水化进程，通过原材料组成计算水化后期的水化程度以及离子浓度即可计算出硬化水泥浆浆体水化后期的电导率.

1.2 基于水化进程的孔隙率和孔隙溶液离子浓度计算

采用Tomosawa模型模拟水泥的水化进程，假定水泥颗粒呈球形，水泥水化过程可分为诱导期阶段、相界面反应过程和扩散反应过程.纯水泥的水化动力学方程用式（6）表示［25-26］：

式中：α为水泥水化度；t为水泥水化龄期，h；Sw为水泥与水接触的有效表面积，g/cm2；S0为无约束下的总表面积，g/cm2；ρw为水的密度，g/cm3；Cw-free为C-S-H凝胶外的自由水量；ρc为水泥的密度，g/cm3；r0为未水化水泥的半径，cm；ϑ为水与水泥质量的化学计量比；wg为C-S-H凝胶结合水量；kd为诱导期反应系数，cm/h；kr为相界面反应系数，与温度有关，遵循Arrhenius定律［27-28］，cm/h；De为水通过凝胶的有效扩散系数，cm2/h.

1.2.1 孔隙率的计算

忽略溶质对溶液体积的影响，基于水泥水化进程，孔隙溶液的体积分数（即液相填充的孔隙率ϕp）可由水的体积减去水化产物中结合水的体积Vb得 到［24］：

1.2.2 孔隙溶液离子浓度计算

硬化水泥浆体中Na+、K+除分布在孔隙溶液，还有部分与水化产物（C-S-H凝胶和水化硫铝酸钙AFm）相结合.根据文献［24］，溶液中Na+、K+的质量为md，水化产物中Na+、K+的质量为mp，md与mp的和即为硬化水泥浆体Na+、K+的总质量mr［24］；假设水泥基材料孔隙溶液是均质的，Na+、K+的浓度为c、体积为V；假设mp与溶液的浓度成正比.可得Na+和K+的浓度c为：

式中：b为“结合因子”，Na+的结合因子为31.0 cm3，K+的结合因子为20.0 cm3［24］.

假设所有水溶性碱都是以硫酸盐的形式存在［24］，不同的水泥可溶性碱与总碱比例不同，根据文献［16］对6种水泥的研究，得到水溶性碱占Na2O、K2O的平均质量分数分别为53%、97%，那么水化产物中非水溶性碱占Na2O、K2O的平均质量分数分别为47%、3%，由此可得Na+和K+的浓度为：

式中：m（Na2O）、m（K2O）分别为水泥中Na2O、K2O的质量，g.

由式（9）、（10）可知，Na+、K+的浓度与水泥组分中Na2O和K2O的含量、水胶比、水化程度密切相关.

1.3 硬化水泥浆体电导率动态计算模型

硬化水泥浆体电导率的计算步骤为：首先，根据水胶比、水泥密度和比表面积，通过式（6）计算出硬化水泥浆体的水化程度；其次，根据水泥组成、水化程度，通过式（3）、（4）、（7）、（9）和（10）计算孔隙溶液离子浓度和液相填充的孔隙率；再利用孔隙溶液离子浓度，通过式（2）计算出孔隙溶液电导率；最后，根据孔隙溶液电导率和液相填充的孔隙率，通过式（5）计算出硬化水泥浆体电导率，实现从原材料到硬化水泥浆体电导率的动态计算.

2 硬化水泥浆体电导率动态计算模型的验证

为检验硬化水泥浆体电导率动态计算模型的可行性，本文对上述步骤进行逐一验证，验证结果及分析见下文.

2.1 硬化水泥浆体水化程度

水泥的密度为3.16 g/cm3，勃氏比表面积为3 450 cm2/g［29］，通过计算可得硬化水泥浆体的水化程度，其试验结果［29］与计算结果见图1.由图1可见：水化龄期相同时，硬化水泥浆体的水化程度随着水胶比的增大而增大；水胶比相同时，水化程度随着龄期的增长而不断地增大，水化前24 h水化速率最快；水泥的水化速率与时间成负相关关系，龄期越大水化速率越小，到500 h时水化速率更为缓慢；与试验结果相比，水化模型能较好地模拟水化程度随时间的演化关系，但24 h内的水化程度计算结果与试验结果差异较大；水胶比为0.30、0.40、0.50、0.60的硬化水泥浆体的水化程度模拟误差分别为26%、23%、25%、27%；对龄期为3、7 d的水泥硬化浆体的水化程度拟合误差在15%以内，而对龄期28、91 d的拟合误差在5%以内.由此可见，随着硬化水泥浆体水化龄期的增长，该模型的计算误差越小.

图1 硬化水泥浆体水化程度的试验结果与计算结果Fig.1 Test and calculated results of hydration degree of hardened cement pastes

2.2 硬化水泥浆体孔隙溶液离子浓度

普通硅酸盐水泥的化学组成（质量分数）见表1［29］，不同水胶比下硬化水泥浆体孔隙溶液的离子浓度见图2.由图2可知：孔隙溶液中离子浓度排 序 为c（OH－）＞c（K+）＞c（Na+）＞，各离子浓度均随着水化龄期的增长而增大，且水化7 d后基本稳定；OH－的浓度约为Na+、K+浓度的总和（见图2（a），c（Na+）、c（K+）、c（OH－）分 别 为0.115 5、0.256 8、0.355 4 mol/L，c（OH－）≈c（Na+）+c（K+））；在相同水化龄期下，随着水胶比的增大，孔隙溶液中各离子浓度均呈下降趋势，这是因为硬化水泥浆体水化龄期相同时，水化程度随着水胶比的增大而增大，导致其所含离子物质的量增加，而水胶比的增大也使溶剂水的体积增大，二者耦合作用使孔隙溶液中K+、Na+、OH－、浓度降低.

图2 不同水胶比下硬化水泥浆体孔隙溶液的离子浓度Fig.2 Ion concentration of pore solution of hardened cement paste under different mw/mB

表1 普通硅酸盐水泥的化学组成Table 1 Chemical composition of ordinary Portland cement

2.3 硬化水泥浆体孔隙溶液的电导率

不同水胶比下硬化水泥浆体孔隙溶液的电导率（σp）见图3.由图3可见：随着水化龄期的增长，硬化水泥浆体孔隙溶液的电导率逐渐增大，但其增速减缓；水化3 d内，σp的增速较快，龄期达到28 d时孔隙溶液的电导率几乎保持不变；当水化龄期为28 d时，水胶比为0.30、0.40、0.50、0.60的硬化水泥浆体孔隙溶液电导率分别为8.25、6.10、4.82、3.97 S/m，随着水胶比的增大，孔隙溶液的电导率呈下降趋势，与孔隙溶液离子浓度变化趋势一致.

图3 不同水胶比下硬化水泥浆体孔隙溶液的电导率Fig.3 Electric conductivity of pore solution of hardened cement paste under different mw/mB

2.4 硬化水泥浆体的电导率

硬化水泥浆体的孔隙率ϕp、电导率σt及其计算误差见表2，其中σt的试验值来自文献［29］.由表2可见：硬化水泥浆体的电导率随着水化龄期的增长而减小，这是因为在水化进行7 d之后，硬化水泥浆体孔隙溶液的离子浓度几乎不发生改变，孔隙溶液电导率变化较小，而随着水化龄期的增长，硬化水泥浆体的孔隙率逐渐降低［30］，这导致了硬化水泥浆体整体电导率的降低；硬化水泥浆体的电导率随着水胶比的增大而增大，这是因为水胶比增大，一方面使载流子的浓度降低，溶液的电导率下降，另一方面传输介质水和传输通道孔隙增加，有利于载流子的传输，导致其电导率增大，综合两者作用，其电导率随水胶比的增大而增大［31-33］.

由表2还可见：水胶比为0.40，龄期为91 d时，计算误差最大为10.00%；水胶比为0.60，龄期为28 d时，计算误差最小为0.63%；当龄期为28 d或水胶比为0.50时，计算误差均在5%以内.综上，硬化水泥浆体电导率演化计算模型能较为准确地计算水化后期（7 d之后）硬化水泥浆体电导率的动态变化，其计算误差在10%及以下.

表2 硬化水泥浆体孔隙率、电导率及其计算误差Table 2 Electric conductivity，porosity and its simulation errors of hardened cement pastes

为进一步验证模型的准确性，对文献［34-35］的试验数据进行了验证，结果见表3.由表3可见，该模型能准确计算出水化后期（7 d之后）硬化水泥浆体的电导率，其计算误差亦在10%以内.

表3 硬化水泥浆体电导率Table 3 Electric conductivity of hardened cement pastes

3 结论

（1）基于水泥水化进程，明确了硬化水泥浆体电导率与水胶比、水泥组分、水化程度的关系，建立了硬化水泥浆体电导率动态计算模型，该模型整体计算误差在10%以内，其中对龄期为28 d的硬化水泥浆体电导率的计算误差小于5%.

（2）该模型能定量表征硬化水泥浆体孔隙溶液离子浓度、孔隙溶液电导率、孔隙率以及硬化水泥浆体电导率随水化龄期的动态变化.随着水化龄期的增长，硬化水泥浆体孔隙溶液离子浓度增大，孔隙溶液电导率也增大，孔隙率和硬化水泥浆体电导率减小.

（3）该模型能定量表征水胶比对硬化水泥浆体电导率的影响.随着水胶比增大，硬化水泥浆体孔隙溶液离子浓度降低、电导率降低，同时液相填充的孔隙率增大，导电传输介质水增加，有利于导电离子的传输，硬化水泥浆体电导率增大.