管子弯曲回弹切线数学模型研究

邵国庆，孟秀文，宫丽彦，周庆林

应用研究

管子弯曲回弹切线数学模型研究

邵国庆，孟秀文，宫丽彦，周庆林

（大连船舶重工集团舾装有限公司，辽宁大连 116013）

为了实现管子弯曲加工精确无余量计算，需要解决管子弯曲后在两个方向上不对称的切线值的精确计算难题。本文通过管子弯曲实验研究，分析计算得出管子弯曲回弹切线数学模型，然后将管子弯曲回弹切线数学模型应用到实际弯管加工中进行验证。为管子无余量弯曲加工、先焊后弯加工奠定了基础，对推进高效的管子弯曲加工应用有一定的指导作用。

管子弯曲 回弹 切线 数学模型

0 引言

弯管的工艺过程是一个复杂的弹性、塑性变形过程[1]。由于无法解决管子弯曲后的延伸长度、回弹角度的精确计算和管子弯曲后在两个方向上不对称的切线值的精确计算，所以国内管件加工企业目前都使用管子弯曲等比近似有余量下料计算方法。这种管子加工工艺方法，在管子下料长度上留有余量，待管子弯曲后再上平台进行测量并调整管件封闭尺寸，切除管子两端的余量。此工艺方法既浪费管子材料，又降低生产效率。若能采用无余量弯管、先焊后弯新工艺，则对实现管材加工的自动化及提高生产效率、节省材料将具有重要的意义[2]。

1 管子弯曲回弹切线数学模型研究

选用同一炉批号中相同规格管子（Φ114×6，炉批号：11-200842）进行了设定弯曲角度的弯曲试验，记录了相应的试验参数，具体如表1所示。将所有参数在坐标系中标识后，分析其显现的曲线发现管子弯曲尾增、首减值均趋于抛物线形状,如图2所示。

图1 管子弯曲首减、尾增示意图

表1 管子弯曲尾增、首减实测数据表（单位mm）

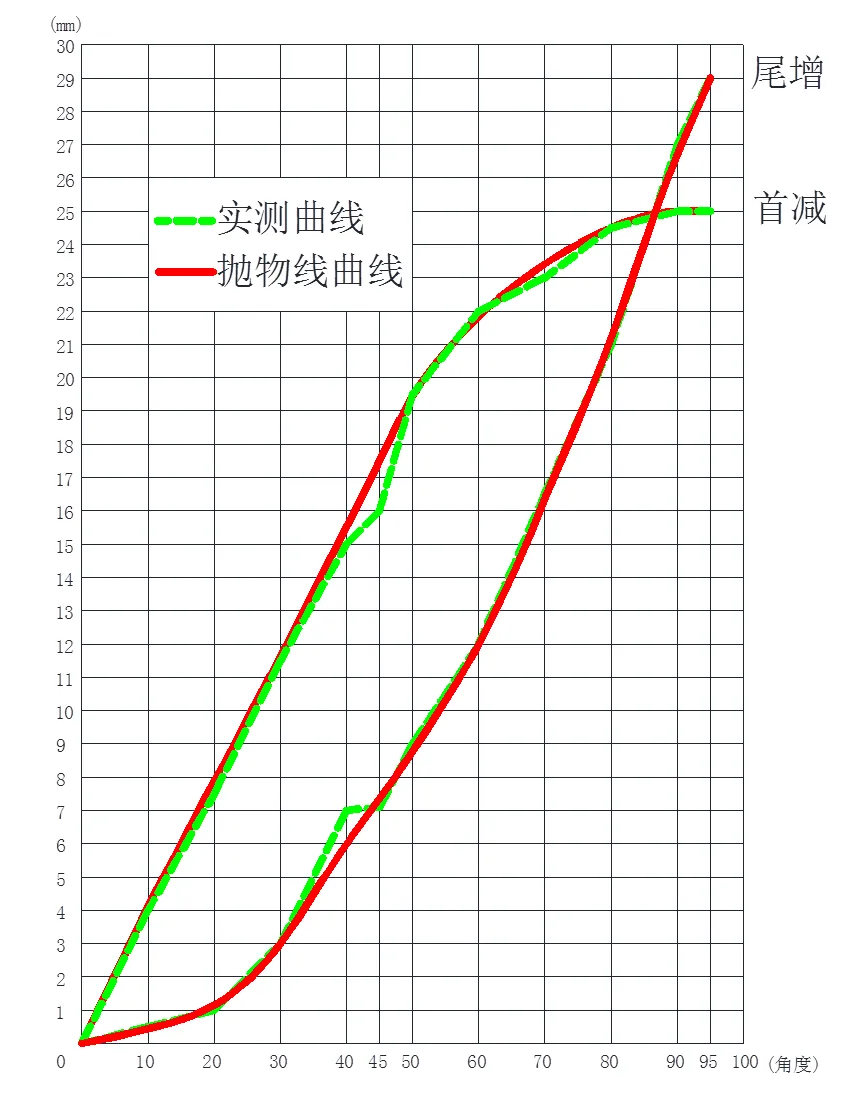
图2 管子弯曲尾增、首减实测数据曲线表

根据图1所示，首部切线长度和尾部切线长度计算公式如下：

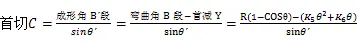
2 管子弯曲回弹切线数学模型验证

应用Φ76×5管子（炉批号：13-200210）试验验证管子弯曲回弹切线数学模型。首先进行两组弯曲试验，实测相应数据参数。弯曲角为30°，尾增为0.5 mm，首减为0.5 mm；弯曲角为92.1°，尾增为5 mm，首减为4 mm。

1）推导尾增数学模型

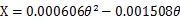
2）推导首减数学模型

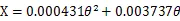
3）首减、尾增的理论计算与试验实测数据对比：

根据以上公式求出弯曲角度对应首减、尾增的理论公式计算数值，与试验实测数据对比，具体如表2所示。

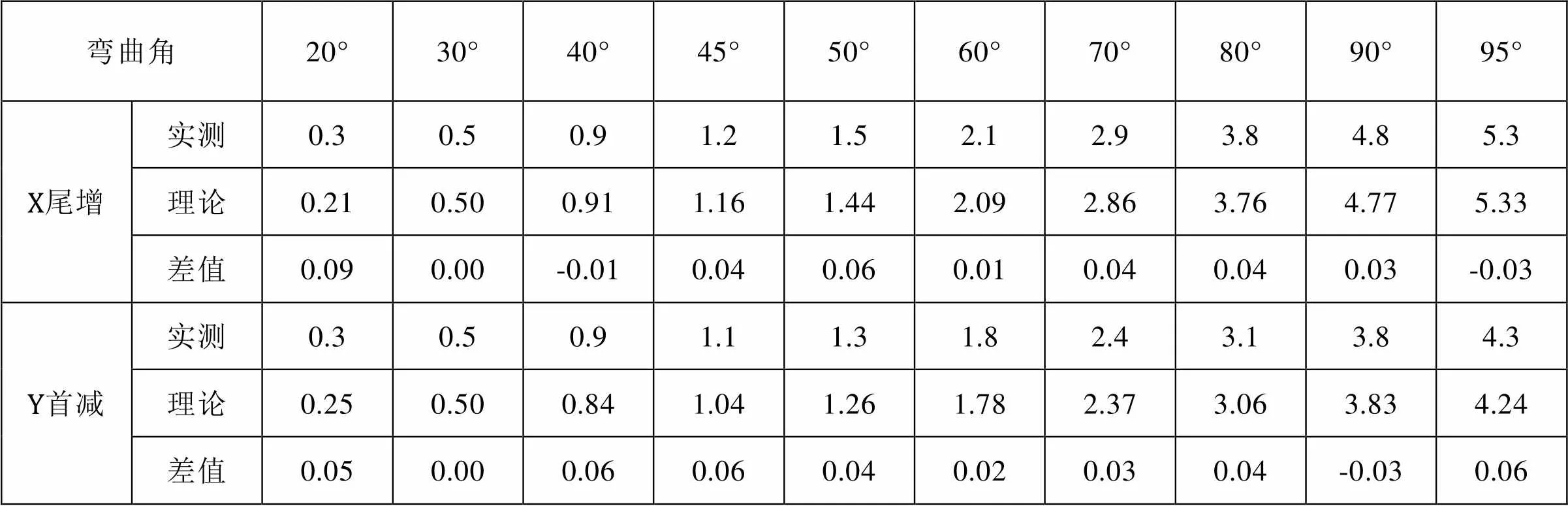
表2 管子弯曲首减、尾增实测数据与理论计算对比表（单位mm）

理论计算数值与试验实测数据对比，两者差值均小于等于±1 mm。

4）首切、尾切的理论计算与试验实测数据对比

应用该口径、炉批号管子弯曲加工成形角45º的管子，应用数学模型和公式计算理论首切、尾切值，同时实测具体首切、尾切值。

记录试验实测参数：弯曲角45.5º、成形角45º、首切97 mm、尾切97 mm。

将弯曲角45.5º，成形角45º代入公式1、公式（2）中，首切=95.78 mm、尾切=97.50 mm。

《中国造船质量标准GB/T 34000-2016》中对管子弯曲后封闭尺寸标准范围是±3 mm。应用数学模型计算的首切、尾切值和试验实测数据相比的误差在-0.5 mm至+1.22 mm之间，低于标准范围要求，验证了尾增、首减数学模型和首切、尾切公式的准确性。

3 结语

本文通过研究回弹前后起弯点在两个切线方向的位移量，即尾增、首减量，找出其中的数学规律并建立数学模型。应用理论计算结果与试验结果对比，确定所研究的管子弯曲回弹切线数学模型的正确性。

结合成熟的管子弯曲回弹角度、延伸值数学模型，就可以完成管子弯曲加工精确无余量下料计算。进而实现无余量弯管、先焊后弯新工艺，能够有效节约管子材料并大幅提高管子加工生产效率。

[1] 董胜利. 弯管工艺过程的受力分析及工艺分析[J].中国西部科技, 2017, 12: 08-11

[2] 胡勇, 王呈方. 智能弯管回弹伸长测量仪的研制及应用[J]. 船舶工程, 1996, (02): 57-60.

[3] 胡勇, 王呈方. 弯管工艺中回弹、伸长和成形半径的确定方法[J]. 锻压技术, 1997, (01): 35-37.

Research on mathematical model of pipe bending springback tangent

Shao Guoqing, Meng Xiuwen, Gong Liyan, Zhou Qinglin

(Dalian Shipbuilding Industry Outfitting Co., Ltd. Dalian 116013, Liaoning, China)

TM611

A

1003-4862（2022）01-0005-03

2021-06-15

国家工信部高技术船舶科研项目：船舶分段智能制造装备解决方案及关键共性技术研究。

项目编号：MC-201906-Z01

邵国庆（1982-），男，高级工程师，主要从事从事船舶舾装件生产技术及管理。Email：13478444642@163.com。