一种新型的樽海鞘群算法及其应用*

谢 聪，郑洪清

(1.广西大学行健文理学院，广西 南宁 530005；2.广西外国语学院信息工程学院，广西 南宁 530222)

1 引言

近年来，随着群智能算法的发展和应用，一系列新的算法被提出，如蜻蜓算法DA(Dragonfly Algorithm)[1]、水循环算法WCA(Water Cycle Algorithm)[2]、布谷鸟搜索CS(Cuckoo Search)算法[3]、灰狼优化GWO(Grey Wolf Optimizer)算法[4]、Jaya算法[5]和鲸鱼优化算法WOA(Whale Optimization Algorithm)[6]等。2017年，Mirjalili等[7]提出樽海鞘群算法SSA(Salp Swarm Algorithm)，它与其他群智能算法一样存在后期收敛速度慢和易陷入局部最优等缺陷。一些学者对其进行了改进，文献[8,9]通过Tent混沌序列生成初始种群并对最优个体采用精英质心拉伸机制，在食物源位置上引入疯狂算子，并且在追随者位置更新公式中引入自适应惯性权重来增强全局搜索能力；文献[10]分别在领导者阶段和跟随者阶段添加衰减因子和动态学习策略来提高算法的全局搜索能力；文献[11]在领导者位置引入上一代樽海鞘群位置并加入了惯性权重策略，提高了算法的寻优精度和稳定性；文献[12]将PSO(Particle Swarm Optimization)算法的随机惯性权重引入SSA的追随者位置更新公式中，其次用差分进化 DE(Differential Evolution)算法的变异操作替代SSA的领导者位置更新操作来提高收敛速度和计算精度；文献[13]通过引入天体运动更新机制来提高算法的收敛速度和计算精度。上述算法虽然在一定程度上提高了算法性能，但仍有提升的空间。

针对以上问题，本文提出一种新型的樽海鞘群算法NSSA(a Novel Salp Swarm Algorithm)，借鉴灰狼优化算法追随α狼的思想，在SSA的追随者位置更新公式中引入GWO算法的追随机制，通过23个基准函数和2个图像匹配问题对算法性能进行评测，验证了NSSA的有效性。

2 樽海鞘群算法

樽海鞘群算法是Mirjalili等根据海洋中的樽海鞘的觅食行为而提出的一种群智能算法，其依靠领导者和追随者的位置更新来完成问题优化。领导者的位置更新公式如式(1)所示：

(1)

c1=2e-(4*l/lmax)2

(2)

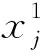
追随者的位置更新利用式 (3)进行(牛顿运动定律)：

(3)

其中,t是时间，a是加速度，v0是初始速度，a=(vfinal-v0)/t,v=(x-x0)/t，追随者的位置更新公式如式(4)所示：

(4)

3 新型樽海鞘群算法

在基本樽海鞘群算法中，追随者的新位置为当前追随者与上一个追随者位置的平均值，在迭代过程中形成链式结构，最终追随至领导者位置，这一追随方式是造成算法收敛速度慢和计算精度差的主要原因。针对基本樽海鞘群算法存在的不足，本文借鉴灰狼算法的ω狼追随α狼的思想替换樽海鞘的追随方式。因此，追随者的位置更新公式如式(5)所示：

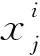
(5)

A1=2*a/r1-a

(6)

a=2-2*l/lmax

(7)

C1=2*r2

(8)

其中，r1,r2∈[0,1]为随机数，其他符号含义与式(1)～式(3)相同。

新型樽海鞘群算法步骤如算法1所示：

算法1新型樽海鞘群算法

步骤1设置种群规模、初始迭代值、最大迭代次数和问题边界等参数。

步骤2在边界范围内随机初始化樽海鞘种群，求出领导者位置和相应值。

步骤3判断是否达到最大迭代次数，如果是，输出领导者和相应值，结束算法，否则进入步骤4。

步骤4首先执行式(2)，然后对每一个樽海鞘执行式(1)；再执行式(5)～式(8)。

步骤5对种群中每一个樽海鞘进行越界处理，求出领导者位置和相应值并判断此时樽海鞘的值是否优于之前领导者值，如果是则用较优值替换较差值。

步骤6迭代次数加1，进入步骤3。

4 图像匹配

基于灰度图像匹配的数学描述：给定2幅灰度图像S和T的大小分别为m1×n1和m2×n2,S和T分别表示原图像和目标图像，T(m,n)表示目标图像上坐标(m,n)处的像素。令m2≤m1,n2≤n1，以S为原图像，T为目标图像，所求解的问题就是在S中搜索T的最优位置，采用归一化积的最大相似度作为目标函数如式(9)所示：

(9)

其中,1≤i≤m1-m2+1,1≤j≤n1-n2+1。

算法2利用新型樽海鞘群算法求解图像匹配

步骤1设置种群规模、初始迭代值、最大迭代次数和问题边界等参数，导入图像数据。

步骤2在边界范围内随机初始化樽海鞘种群，利用式(9)求出领导者位置和相应值。

步骤3判断是否达到最大迭代次数，如果是，输出领导者和相应值，结束算法，否则进入步骤4。

步骤4首先执行式(2)，然后对每一个樽海鞘执行式(1)；再执行式(5)～式(8)。

步骤5对种群中每一个樽海鞘进行越界处理，利用式(9)求出领导者位置和相应值，并判断此时樽海鞘的值是否优于之前领导者值，如果是则用较优值替换较差值。

步骤6迭代次数加1，进入步骤3。

5 仿真实验与结果分析

为了验证NSSA的性能和图像匹配的效果，分别进行实验1和实验2。实验1采用23个基准函数，并与其他算法进行性能比较；实验2采用2个图像匹配案例，并与其他算法进行性能比较。所有实验均运行在处理器为Intel Celeron(R)双核CPU T3200,2.90 GHz、内存为4 GB的Windows PC机上，以Matlab R2010a编写代码。

5.1 实验1

用NSSA来求解全局优化问题，并与LECUSSA(LEvy flight-based Conditional Updating Salp Swarm Algorithm)[14]、SSA、WCA、CS、GWO和Jaya算法进行性能比较。所有算法的种群规模为30，最大迭代次数为500，23个基准函数如表1所示，其中Dim,Range和fmin分别表示维度、取值范围和理论最小值；f1～f7为单峰值函数；f8～f23为多峰值函数。

Table 1 Benchmark functions

7种算法求解23个基准函数的结果如表2所示，每种算法独立运行30次，结果均为30次实验结果的平均值和标准差，加粗字体表示与其他算法比较时求解的最小值和标准差。从表2可知，对函数f6、f15和f20而言，NSSA求解的最优值比WCA、LECUSSA和CS算法求解的效果稍差。对其余20个函数中的5个函数：函数f14，NSSA求解效果与CS算法的一致；函数f16和f18，NSSA求解效果与LECUSSA、SSA、WCA和CS算法的一致；函数f17和f19，NSSA求解效果与SSA、WCA和CS算法的一致。对其他15个函数，NSSA求解效果均优于其他算法，尤其是对函数f3、f8、f9、f11、f21、f22和f23而言，NSSA求解的最优值均达到了理论最优值，而未达到理论最优值的结果也比其他算法的求解精度提高了几到几百个数量级。另外，从标准差可知，NSSA算法的鲁棒性亦优于其他算法。

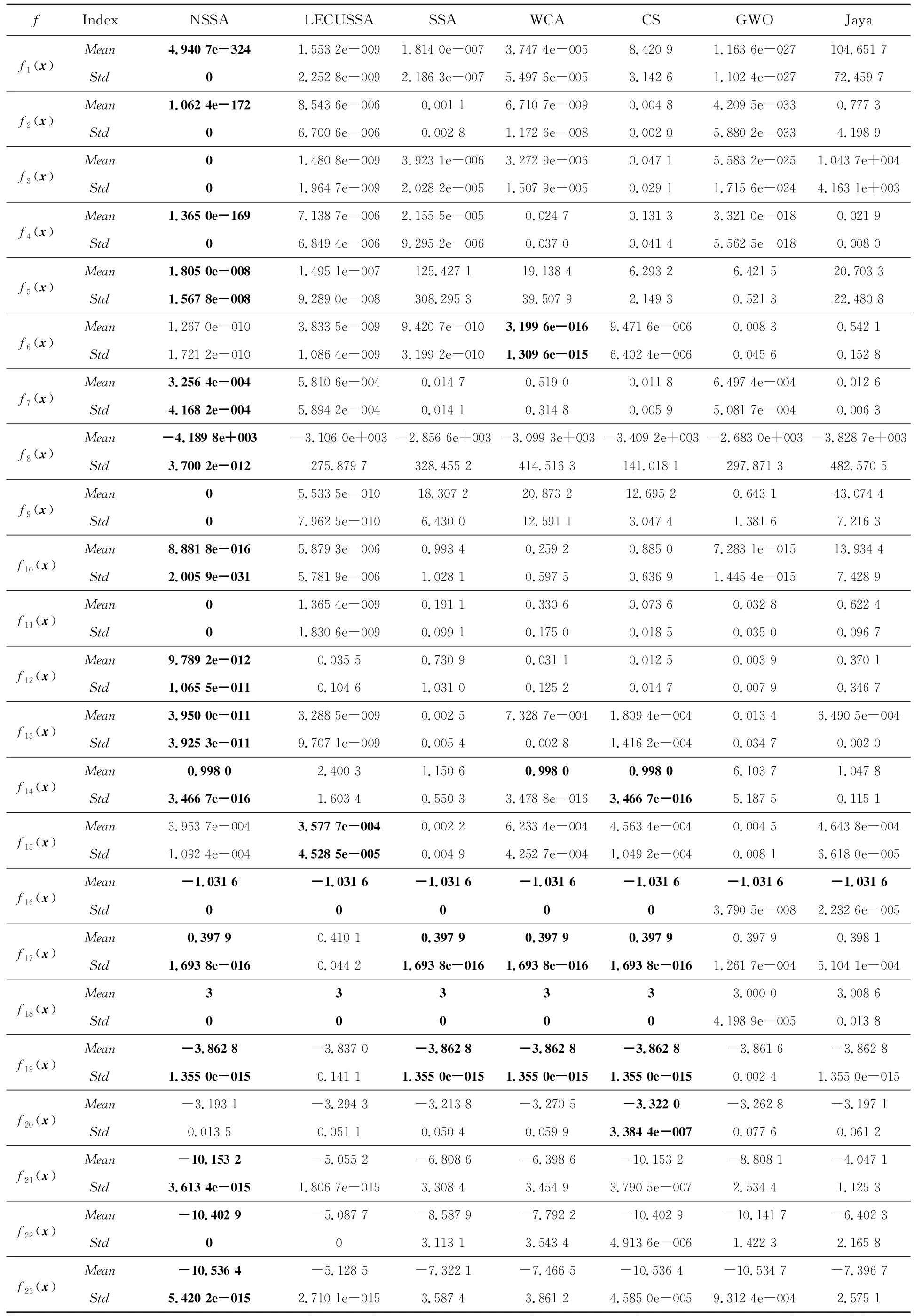
Table 2 Optimization results on benchmark functions

图1～图4给出了NSSA与其他6种算法在部分基准函数上的平均适应度曲线，从图1和图2可知，虽然NSSA初值收敛速度不是最快，但中后期进化明显(由于线条重叠难以分辨，但从表1的函数值可知)；从图3～图4可知，在初期和中后期NSSA收敛速度均为最快。

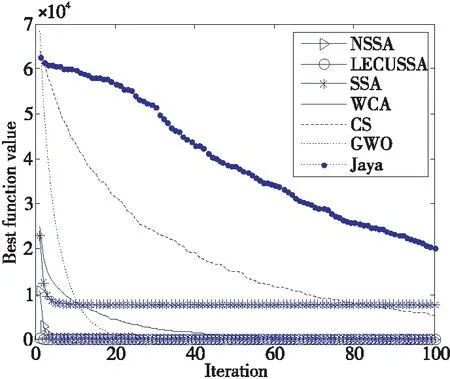
Figure 1 Average optimization curve on f1图1 f1函数上的平均优化曲线

Figure 2 Average optimization curve on f2图2 f2函数上的平均优化曲线

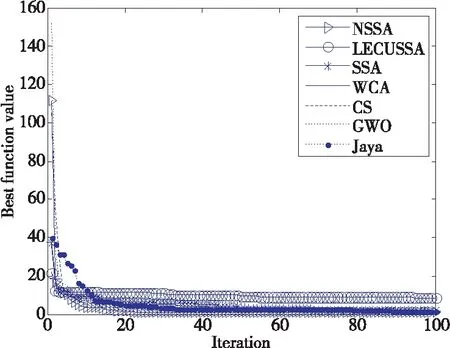
Figure 3 Average optimization curve on f14 图3 f14函数上的平均优化曲线

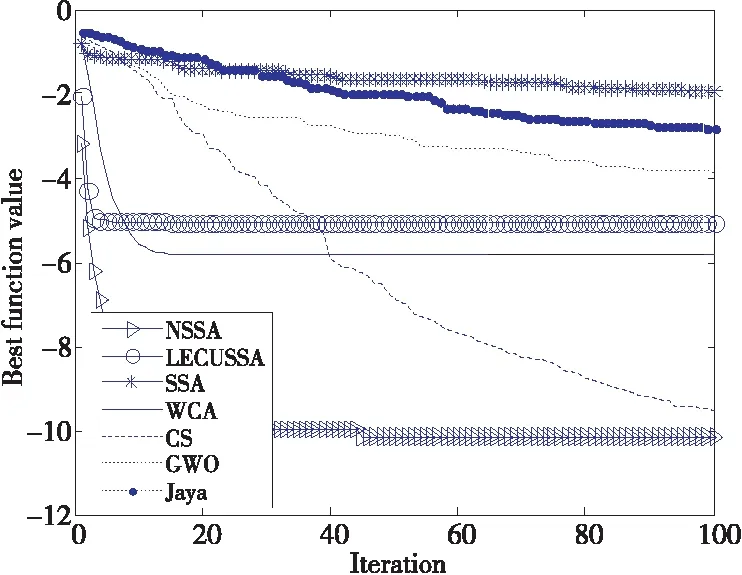
Figure 4 Average optimization curve on f21 图4 f21函数上的平均优化曲线

5.2 实验2

将NSSA应用于图像匹配，并与其他4种算法进行比较，所有算法种群规模为30，最大迭代次数为100。

首先验证NSSA在无噪声环境中的有效性，以分辨率为512×512的Lena图像为原图像，取该图坐标(220，220)为左上角，截取分辨率为100×100的子图作为目标图像，理想适应度值为1。

原图像和目标图像分别如图5a和图5b所示，利用NSSA进行图像匹配的结果如图5c所示，图中的黑色框线表示匹配到的实验结果。

Figure 5 Result of matching Lena image with NSSA 图5 NSSA匹配Lena图像的结果

为了展示NSSA的有效性，将其迭代次数与平均适应度值关系的仿真结果与其他算法比较，如图6所示。由图6可知，NSSA在30次迭代过程中，大约在30代左右达到理论最优值1，而此时其他算法平均适应度值均未达到最优。另外，30次实验的平均运行时间(平均运行时间为达到理论值1所需时间，即为匹配成功的时间)及匹配率如表3所示。由表3可知，本文NSSA的平均运行时间仅为0.093 s，匹配率为100%，可见NSSA的匹配速度和匹配精度远优于其他算法。

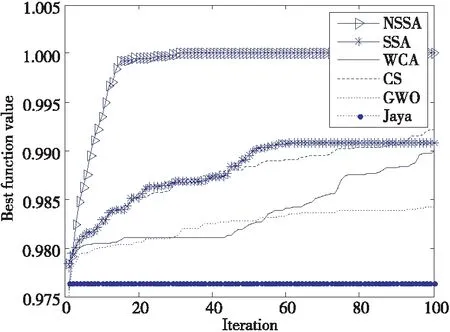
Figure 6 Comparison of average convergence curve of 6 algorithms图6 6种算法平均收敛曲线比较

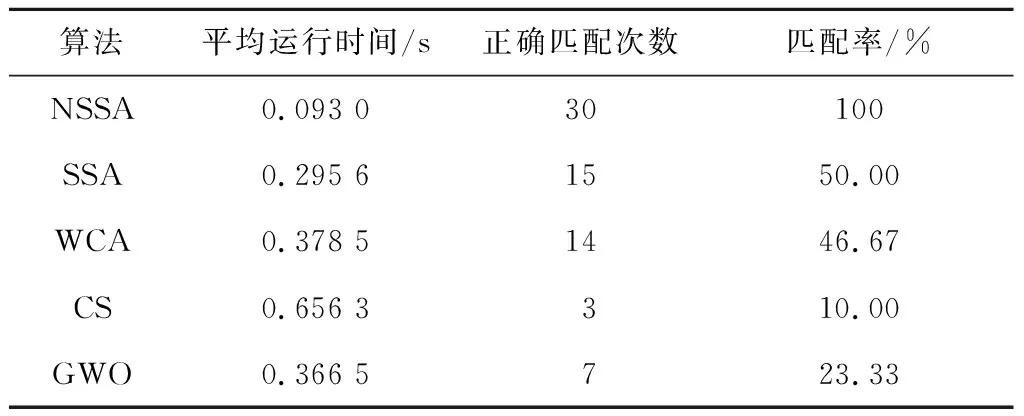
Table 3 Comparison results of each algorithm on Lena

再验证NSSA在有噪声环境中的有效性，选取分辨率为512×512的Couple图像进行测试，取该图坐标(123,131)为左上角，截取分辨率为100×100的子图作为目标图像，理想适应度值为1。给原图像和目标图像添加均值为0、方差为0.05的高斯噪声，分别如图7a和图7b所示，利用NSSA进行图像匹配的结果如图7c所示，图中的黑色框线表示匹配到的实验结果。另外，30次实验的平均运行时间(平均运行时间为达到最大迭代次数所需时间，因为此时无法达到理论最优值1)及匹配率如表4所示。由表4可知，在高斯噪声下的Couple图像，NSSA的匹配成功率依然最高，为93.33%，且耗时在0.45 s左右。虽然所有的算法都能成功匹配，但目标函数值均不能达到理论最优值1。综上所述，所有的实验均表明了NSSA具有更好的收敛速度、匹配精度和鲁棒性。

Figure 7 Result of matching Couple image with NSSA 图7 NSSA匹配Couple上图像的结果

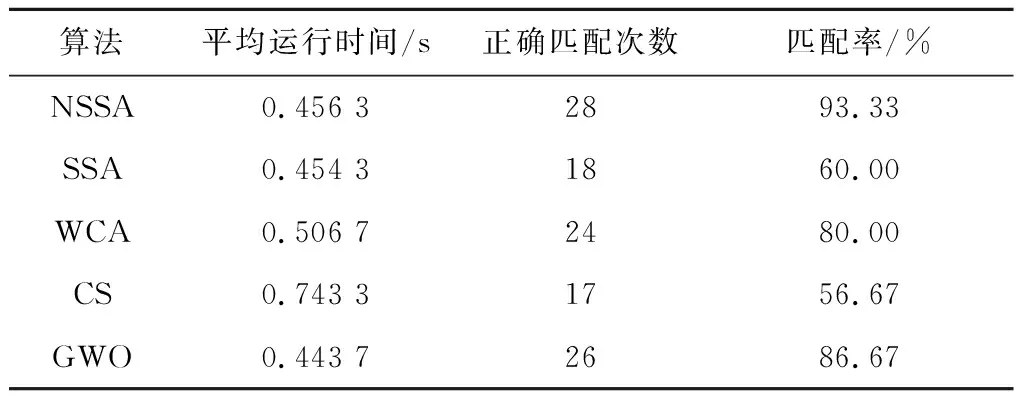
Table 4 Comparison results of each algorithm on Couple

6 结束语

本文针对基本樽海鞘群算法在后期收敛速度慢和易陷入局部最优等缺陷，分析了樽海鞘的追随领导者方式是造成其缺陷的主要原因，借鉴灰狼优化算法中ω狼追随头狼的思想替换樽海鞘追随领导者的方式，提出一种新型的樽海鞘群算法NSSA。通过23个基准函数和无噪声及有噪声图像匹配的仿真实验表明，所提算法具有更好的收敛速度、计算精度和鲁棒性。