基于并行的区块链异常交易检测随机森林模型研究

赵永斌，陈 苗，李 涛，尤军考

(1.石家庄铁道大学信息科学与技术学院，河北 石家庄 050043;2.中国铁路北京局集团有限公司石家庄电务段，河北 石家庄 050000;3.中国移动通信集团河北有限公司，河北 石家庄 050000)

0 引言

比特币作为区块链的首个广泛应用，伴随着区块链技术发展逐渐成为区块链研究的重点。作为第一个公开使用的私人数字货币，其具有去中心化、匿名性、转账成本低、全球流通便捷等特性，降低了人们踏入金融行业的门槛[1]。但是，由于加密货币不受政府控制，允许个人和组织绕过法律及监管部门的监管，由此导致洗钱等一些非法交易逐渐猖獗。根据美国联邦调查局(FBI)的报告称，从2015年到2017年，与虚拟货币相关的案件增长了近6倍，仅在2018年上半年中，加密货币犯罪就在2017年全年数量的基础上增长了3倍。2020年，Mirror Trading International在南非实施了世界上最大的加密货币骗局，数十万受害者被骗走了价值5.88亿美元的比特币。2021年4月，南非再次出现了更大一起的加密货币案件，一家名为Africrypt公司的两位创始人，在几个小时内从投资者那里窃取了36亿美元。Chainalysis发布的最新加密犯罪报告指出，俄罗斯、中国、美国、英国、法国、乌克兰、韩国、越南、土耳其和南非是从非法地址接收加密货币数量最多的国家[2]。因此，对以比特币为代表的区块链异常交易行为检测刻不容缓。

异常交易检测方法主要分为无监督、有监督两类。无监督学习技术包括自组织映射[3]和Peer Group Analysis[4]；监督学习技术有决策树[5]、逻辑回归[6]、贝叶斯信念网络(贝叶斯网络)[7]、关联规则[8]、支持向量机[6]、遗传算法[9]。近年来，发展起来的基于多学习器组合的集成学习方法，在欺诈检测领域取得良好的效果。2018年，Navanushu Khare等人在高度倾斜的欺诈数据集上进行了逻辑回归、随机森林、决策树、SVM对比实验，指出随机森林效果明显优于其他算法[10]。同年，Massimo Bartoletti等人进行了多组对比实验，实验同样表明随机森林方法是检测庞氏骗局最为有效且通用的方法[11]。2019年，Mark Weber等人指出：逻辑回归具有较强的可解释性，随机森林具有较强的准确性，能有效用于比特币反洗钱检测[12]。随机森林准确性较高但训练时间较长，逻辑回归虽然训练时间较短但准确性较差，因此本文提出了一种并行随机森林训练模型的方法，通过创建多个进程并行处理计算任务，提升数据计算的效率，有效解决了随机森林训练时间较长的问题。

1 相关技术与研究

1.1 逻辑回归

目前逻辑回归主要用于解决二分类问题，其内容主要包含假设函数、决策边界、代价函数和参数优化[13]。

(1)假设函数。构造假设函数以多变量线性回归为基础，综合考虑多个变量得到其线性组合。二分类采用非线性函数 Sigmoid将线性回归计算的结果映射到[0,1]区间。计算逻辑回归的假设函数为式(1)所示。

(1)

其中x为多维输入变量，θ为多维输入变量对应的权值。

(2)决策边界。经过sigmoid非线性函数可以将任意连续值映射为 [0,1] 区间内的值，但并不是二值映射，为得到二分类问题的最终结果，可以通过设定决策边界来将连续值转化为离散的二值。例如设定的边界为0.5，函数的输出大于0.5时，即将该结果视为1，否则视为0。

(3)代价函数。代价函数用于评判对实际问题拟合效果的好坏。代价函数越小代表模型在实际问题上的适应性越好，反之则越差。逻辑回归的代价函数计算训练集中每一个样本的偏差值并取平均，为更好地适应二分类问题会对每个样本的偏差进行对数运算，代价函数的计算如公式(2)所示，代价函数的向量化表示见公式(3)。

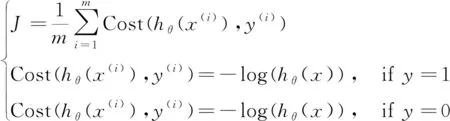
(2)

(3)

其中x为多维输入变量，θ为多维输入变量对应的权值，h为样本对应的实际输出。

(4)参数优化方法。不断修改权值使代价函数减小的过程即为参数优化。采用梯度下降算法更新逻辑回归参数[14]，通过不断计算代价函数关于权值的梯度，并利用梯度负方向为函数下降速度最快的方向这一准则更新权值，使代价函数能随梯度的更新不断下降。对式(2)所示代价函数的构造形式，可得到其相对于各个权值的梯度，从而得出权值的更新规则，如公式(4)所示，权值更新规则的向量化表达公式(5)所示。

(4)

(5)

其中α为学习率，其大小代表了参数更新的速度。

1.2 随机森林

随机森林由多棵决策树组成，决策树是一种非常典型的分类方法，其形状像一棵树，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点则代表一种类别。目前经典的决策树算法有ID3、C4.5和CART[15]。决策树中的相关概念如下：

(1)信息。香农指出信息是事物运动状态或存在方式的不确定的描述[16]。在决策树中，集合分类后，某类中事件xi的信息量定义为：

I(X=xi)=-log2(p(xi))

(6)

其中I(x)用来表示随机变量的信息量，p(xi)为随机事件xi发生时的概率。

(2)信息熵。信息熵用于衡量事件集合的不确定性，当熵越大，集合的不确定性越大，反之则越小。事件集合X熵的定义如下：

(7)

对于机器学习中的分类问题，熵越大表示该类别的不确定性越大，反之则越小。

(3)信息增益。ID3决策树算法中使用信息增益作为选择特征的指标，增益越大，则代表这个特征的选择性越好。信息增益的具体定义如下：

Gain(X,A)=H(X)-H(X|A)

(8)

其中H(X)是事件集的熵，H(X|A)是按照属性A划分后的条件熵。

(4)信息增益率。在C4.5决策树算法中使用信息增益率作为选择特征的指标，优化了信息增益偏向值个数多的属性的缺陷。具体公式如下：

(9)

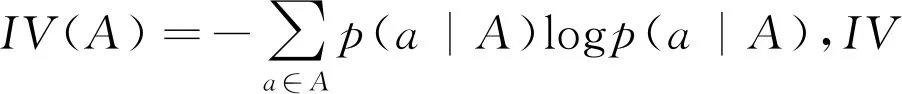
(5)基尼指数。CART决策树算法中基尼指数作为选择特征的指标，代表数据的纯度。基尼指数越大，则代表数据越不纯，也就说明不确定性越大，进行分类也就越困难。

(10)

其中p(x)表示样本属于某个类别的概率。

随机森林属于集成算法中的Bagging类型，训练多个弱分类器，各自独立做出预测，将弱分类器的结果进行投票得到最后结果，使模型得到的最终结果拥有较高的泛化能力和精确度。随机森林之所以能具有较好的效果，是因为“随机”使模型具有抗过拟合能力，“森林”使模型更加准确。

1.3 区块链异常交易检测数据集

Elliptic数据集[17]进行区块链异常交易检测，数据集包含合法的真实实体和非法实体。合法实体有矿工、钱包提供商、交易所等。非法实体有恐怖组织、诈骗、庞氏骗局、恶意软件、勒索软件等，共计203769个节点交易以及234355条边，其中4545笔交易被标记为非法，42019笔交易被标记为合法，其余未被标记，其中合法与非法标记过程是由基于启发式的推理过程决定。根据时间戳，此数据集将交易划分为49个时间步长。每笔交易具有166个交易相关特征，其中有原生特征94个，如时间步长、手续费等；聚合特征72个，如从中心节点向前/向后一跳聚合事务信息计算得出的最小值、最大值、相关系数和标准差等[12]。

本文采用Elliptic数据集中的前26个特征，随机选取21000条已标记数据，按照7∶3划分训练集，测试集。实验数据集各类别数量如表1所示。

表1 样本数量分布

1.4 基于逻辑回归的区块链异常交易检测

Mark Weber等人曾采用逻辑回归进行区块链异常交易检测，其采用Elliptic数据集中带标签的全部数据按照7∶3划分训练集，测试集[12]。首先对Elliptic数据集进行预处理，然后训练得到逻辑回归模型，最后通过模型检测异常交易。使用逻辑回归进行区块链异常交易检测流程如图1所示。

图1 基于逻辑回归的区块链异常交易检测

1.5 基于随机森林的区块链异常交易检测

Mark Weber等人曾采用随机森林进行区块链异常交易检测，其采用Elliptic数据集中带标签的全部数据按照7∶3划分训练集，测试集[12]。过程中采用Bootstrap抽样的方法得到各棵决策树的训练集，通过各棵决策树得出测试结果，最终再通过投票得出区块链异常交易检测的结果。训练测试m棵决策树的随机森林异常交易检测过程如图2所示。

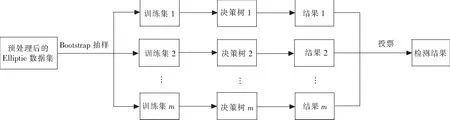
图2 随机森林模型

此方法没有利用好每棵决策树都相互独立的特点，导致训练时间过长，所以完全可以开启多个进程，让每个进程并行生成决策树进行异常交易检测，优化训练耗时较长的弊端。

2 基于并行随机森林的区块链异常交易检测

2.1 并行随机森林检测模型

并行随机森林进行区块链异常交易检测的过程中采用预处理后的Elliptic数据集，生成多个进程，由各个进程共同承担建树的任务，运用Bootstrap抽样的方法得到各棵决策树的训练集，生成决策树后预测结果，各进程检测结果通过投票得出，最后再通过各进程检测结果投票得出最终结果，n个进程并行训练m棵决策树的随机森林异常交易检测过程如图3所示。训练多进程随机森林模型的具体过程为：

Step1计算每个进程应生成决策树的个数， tree_nums←随机森林中决策树的数量(n_estimators)/进程数(n_processes)。

Step2生成n_processes个进程，再分别将训练集、标签集、决策树参数等信息传入单进程训练函数进行训练。

进程代码如下：

#detree_queue，决策树队列；i, 进程号；tree_nums，进程中需生成决策树的个数；Tr，训练集；Te，标签集；detr_args，决策树参数；processes，进程列表

for i in range(self. n_processes):

p =Process(target=signal_train, args=(self.detree_queue, i, tree_nums , Tr, Te, detr_args))

p.start()

processes.append(p)

for p in processes:

p.join()

Step3单进程训练函数(signal_train)训练tree_nums棵树，每棵树用bootstrap方法生成的训练集训练决策树，最后将决策树存入队列(随机森林)。

图3 并行随机森林模型

2.2 实验环境

实验采用联想LiCO智能超算平台，单节点16核进行训练，本地计算机配置为Intel(R) Core(TM) i5-4210M CPU @ 2.60GHz，8.00 GB内存。编程语言为python3.6.8，编程中采用scikit-learn库，随机森林与并行随机森林实验中参数n_estimators设置为500，其他参数选取为默认值。

2.3 实验结果分析

2.3.1 评价指标

区块链异常交易检测采用precision，recall和F1三个指标衡量实验效果，具体定义如下：

(11)

(12)

(13)

实验中异常交易为正例(positive)，正常交易为负例(negative)。TN代表实际与检测结果皆为异常交易的个数。FP代表实际为异常交易，但检测结果为正常交易的个数。FN代表实际为正常交易，但检测结果为异常交易的个数。TP代表实际与检测结果皆为正常交易的个数。

2.3.2 逻辑回归实验

表2列出了基于逻辑回归的区块链异常交易检测结果。虽然训练时间仅为0.163s，但其较低的precision、recall、F1表明逻辑回归不适合成为检测区块链异常交易的方法。

表2 逻辑回归异常交易检测结果

2.3.3 并行随机森林实验

表3列出了随机森林与2-8进程并行随机森林模型的异常交易检测结果。在采用同样环境和数据集的情况下，结果表明随机森林和不同进程数并行训练出的随机森林模型在precision,recall,F1上保持一致，且具有较高的分类准确性。

表3 随机森林及多进程并行随机森林的异常交易检测结果比较

为了进一步验证实验结论，分别进行了14000条和7000条样本的对比实验，并行随机森林模型的训练时间均明显下降，如图4、图5所示。

图4 不同样本量数据集进程数与训练时长的关系图

图5 不同样本量数据集训练时间下降率图

从实验结果看，不同样本量数据集的并行随机森林在训练时间下降率上并没有明显差异。随着进程数取值越大，训练时长下降的效果也越来越好，当八进程并行训练随机森林时，时间下降率可达到85%左右，但整体并不是呈线性趋势，时间下降先快后慢，当进程数逐渐增多时，出现时间下降不明显的现象。因此如何能更好地平衡运算时间和通信时间极为重要。当运算时间所占比例越多，通信时间所占比例越少的时候并行运算效率达到最大。仿真实验表明基于多进程并行随机森林的区块链异常交易检测在不降低准确性的同时，节省了大量训练时间。

3 结论

针对以比特币为代表的区块链异常交易检测，在分析随机森林与逻辑回归训练模型的特点基础上，提出了并行随机森林训练模型，此模型在不降低准确性的前提下，大幅减少了训练时间，为区块链异常交易检测技术提供了新的解决方案。在今后的研究工作中，将深入优化基于并行随机森林的异常交易检测算法，提高检测的效率与准确性。