山东省Ångström-Prescott日照辐射模型的参数优化

田晓旭,田辉,张鹏,刘福胜,张倩*

山东省Ångström-Prescott日照辐射模型的参数优化

田晓旭1,2,田辉2,张鹏2,刘福胜2,张倩1,2*

1. 中国农业科学院农田灌溉研究所/农业部节水灌溉工程重点实验室, 河南 新乡 453002 2. 山东农业大学水利土木工程学院, 山东 泰安 271018

Ångström-Prescott模型是基于日照的最佳太阳辐射(R)模型，但由于缺乏模型参数，其应用往往受到限制。为了获得山东省准确的模型参数，本文采用FAO推荐值和根据地理位置、多年平均温度等数据拟合的四种参数化方程，在山东省有实测太阳辐射数据的3个站点（福山、济南和莒县）应用Ångström-Prescott公式计算太阳辐射值，并与实测值和校正参数预测值进行比较。结果表明：（1）3个站点中，福山参数模型估算效果最好，莒县次之，济南最差。福山、莒县和济南的决定系数2分别在在0.9559～0.9661、0.9358～0.9397及0.9083～0.9115之间，但决定系数2都在0.9以上，不同参数化方法预测的R与实测值相关性较高；（2）公式1参数模型估算太阳辐射值效果最好。该公式的平均偏差（）、均方根误差（）及相对均方根误差（）分别在-4.54×10-5～1.23×10-3MJ/(m2/d)、0.021～0.078 MJ/(m2/d)及15.23%～55.40%之间，和校正值比较接近，FAO推荐值估算精度较低，其估算精度远低于公式1。因此，在山东省可以用公式1（=5.43742×10-4+0.149=0.00964×-0.62367）即用海拔和经度较为精确的预测太阳辐射。

太阳辐射; 模型; 参数优化

太阳辐射（R）作为一种重要的气象因子，在地理学科、水利学科、水文与水资源学科等都有着重要的意义，尤其在参考作物增发蒸腾量（0）的估算中发挥着重要的作用，因此获得准确的太阳辐射数据就显得尤为重要。

尽管太阳辐射在诸多学科中都有重要应用，但是由于观测成本、维护和校正的要求，使得我国有太阳辐射实测数据的气象站点并不多。即使在有太阳辐射观测数据的站点，也有很多天由于设备故障和其他问题导致R值丢失或数据质量有问题[1]，为了解决这一问题，提出一种参数化的方法来解决这一问题显得尤为重要。

太阳辐射测量的缺乏导致了间接方法的发展，如经验模型、机器学习方法以及卫星遥感方法。由于经验模型结构相对简单，使用方便，投入也容易获得，因此最常被采用。1998年，FAO56 Penman-Monteith公式中[1]推荐了基于日照时间法的太阳辐射估算模型，也是目前广为应用的一种模型。近年来，国内外学者在基于Å-P公式估算太阳辐射量方面开展了大量的研究Liu X[2]等，Yin YH[3]等、胡庆芳[4]等、贺兴宏[5]等、Liu XY[6]等、李曼曼[7]等和彭世彰[8]等基于中国辐射观测站资料评估FAO56推荐的太阳辐射参数在中国、黄河流域、云南省和江苏射阳等一系列地区的适用情况。

尽管国内外学者对太阳辐射与日照时数关系进行了大量的研究，但在中国各地区Å-P公式模型的、系数修正研究较少。由于缺乏A-P校正参数，国内直接使用FAO推荐值的做法相当普遍，特别是在参照作物腾发量的计算中。

由于不同地区气候、地理位置的差异，Ångström- Prescott公式在不同地区应用有一定差异性，为提高估算精度，本研究以山东省济南、福山、莒县三个站点的多年实测太阳辐射资料为基础，对A-P公式的参数进行校正，与FAO推荐值进行对比，提出4种基于高程、经度、纬度、多年平均气温的参数化公式，并对A-P公式参数对辐射估算的影响进行评价，以期为山东省太阳辐射的准确估算提供参考。

1 材料与方法

1.1 站点数据选择与分析方法

本文选取福山、济南、莒县3个站点进行分析评价，3个站点的基本资料见表1。

表 1 站点基本信息

用评价指标进行评价时，需要将,和R的日实测数据带入公式（1）估算R值，本文所用的日实测数据全部由中国气象局信息中心提供，尽管这些数据已经经过了初步的数据质量控制，但为了进一步提高结果的可靠性，本文采用和前人一致的数据质量控制标准：1）若某日实测资料其中之一缺测，或都缺测，则删除该日数据；2）若R/R或/大于1，则删除该日数据；3）若一个月内缺测数据超过10个，则删除该月数据。

本文先选取3个站点共25年的日实测资料（表1），按照年份先后顺序对数据进行分割，其中，前4/5的数据作为训练数据集进行数据拟合，后1/5数据作为测试数据集用于验证公式，采用平均偏差（MJ/(m2/d)）、均方根误差（MJ/(m2/d)）、相对均方根误差（%）、决定系数2对A-P公式进行评价。

1.2 A-P计算公式

Angstrom-Prescott 公式的表达式为：

R=(+×/)a(1)

式中R、R分别为太阳总辐射和大气顶层辐射MJ/(m2/d)；、为A–P模型参数，二者之和为晴空条件下辐射传输率；、分别为实际与理论日照时间，h。

公式（1）中的R和参照Allen RG[9]等和Liu XY[6]等中所给，计算公式如下：

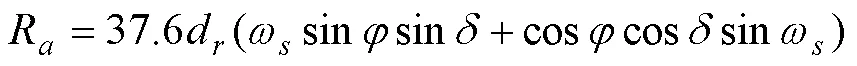
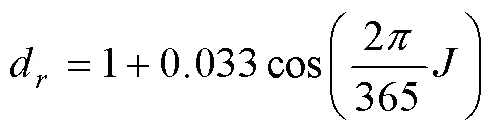
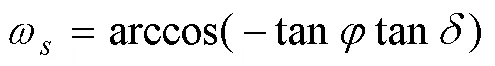
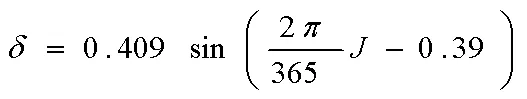
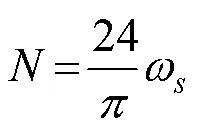
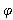
表 2 A-P参数相关性分析

注：**在0.01级别（双尾），相关性显著。下同。

Note: ** showed that there was significant difference at 0.05 level. The same as follows.

尽管有研究[7,10]表明，A-P参数,随着时间的变化而变化，但是根据Liu XY[11]等在中国20个温带气候观测点研究发现，在R预测中，时变的A-P系数并不优于固定的A-P系数，也就是说，时变的A-P系数与固定的A-P系数的预测效果在统计意义上是大致相同的，因此，本文仅讨论固定的A-P参数的参数化方法，本文所评价的5种参数化方法中，前四种是根据A-P参数与站点的基本资料之间的相关性建立，第五种取自FAO[9]的推荐值，具体的参数化公式为：

公式1：=5.43742×10-4+0.149(7)

=0.00964×-0.62367 (7)

公式2：=5.43742×10-4+0.149 (8)

+=-0.0172×T+0.86716

公式3：=-0.02262×+1.00035 (9)

+=-0.0172×T+0.86716

公式4：=0.00964×-0.62367 (10)

+=-0.0172×T+0.86716

FAO:0.250.50 (11)

根据参数化公式（7）～（10），首先计算参数或，然后再计算参数或+，最后通过相加或者相减得到另外一个参数，采用这样的方法，主要是因为不同系数与不同站点基本资料常规因子相关性不同（表1），本文采用系数与站点基本资料常规因子相关性显著的方法，确保得出来的数据准确可靠。指标计算如下：

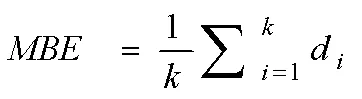
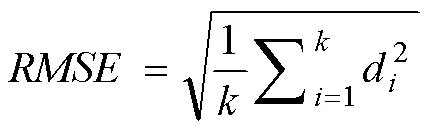
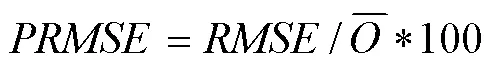
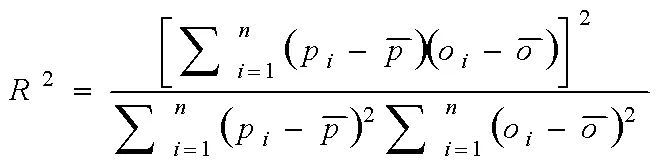
、及的值越小，模型的预测效果越好。统计值用于辨识参数化预测结果与实测值以及校正参数预测结果之间是否存在显著差异，统计值越小，差异越不显著。决定系数2反映了站点和参数化方程的拟合优度，决定系数2越大（越接近1），表明站点和参数化方程拟合效果越好。

2 结果与分析

2.1 a,b参数化结果与校正值的比较

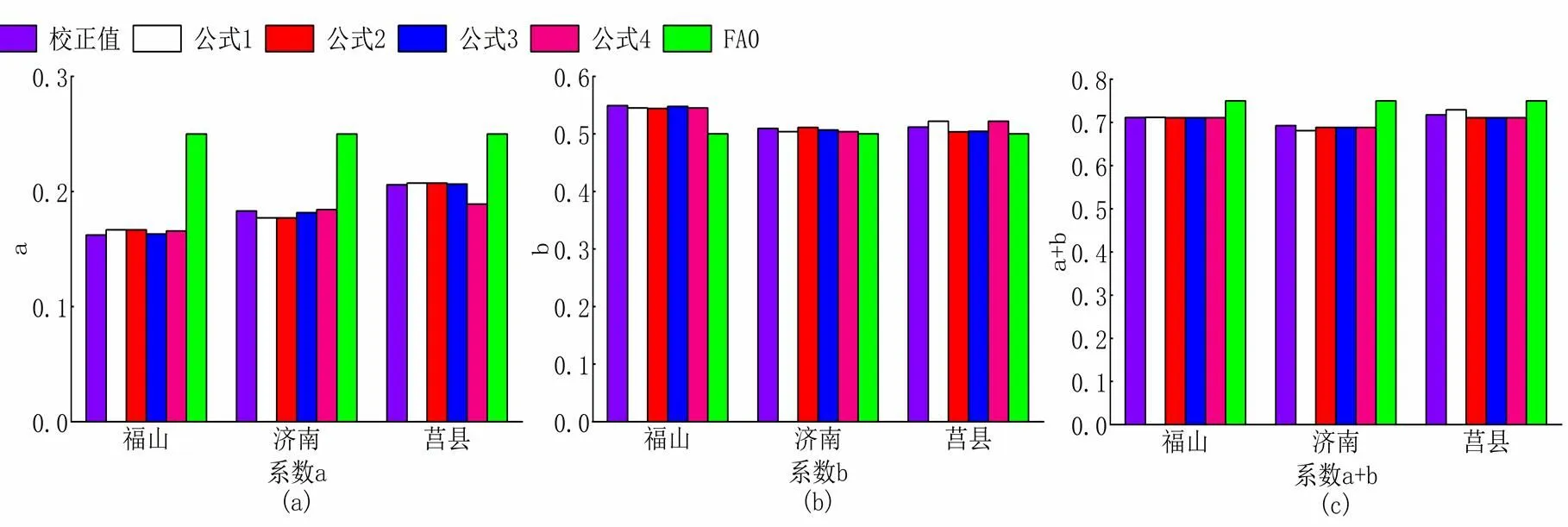
图 1 三个站点a、b参数化结果与校正值的比较

图1是福山、济南、莒县三个站点、、+参数化结果与校正值的比较图，由图（a）可以看出，由公式1、2、3预测得到的系数数值在三个站点相差不大，公式4在福山、济南两个站点预测得到的系数与公式1、2、3得到的结果类似，公式4预测得到系数与校正值相比，在莒县站点较其他站点相差较大，较公式1、2、3平均低估1.8%。公式1、2、3得到的系数a的预测值与校正值最接近，二者平均相差仅为0.001%公式4得到的系数的预测值与校正值平均相差-0.402%，FAO的推荐值与校正值偏差最大，平均高估6.627%，特别是在福山，更是高估8.779%。就站点而言，系数的预测公式在济南的预测效果最好，预测值与校正值的差异在-0.601%～0.119%，平均-0.308%；在福山的预测效果次之，预测值与校正值的差异在0.089%～0.449%，平均0.334%。在莒县的预测效果最差，预测值与校正值的差异在-1.676%～0.154%，平均-0.326%；

由图（b）可以看出，由公式1、2、3、4预测得到的系数数值在三个站点相差不大，其中公式1和公式4在莒县的预测结果类似。公式1、公式4系数预测值与校正值最为接近，二者平均相差仅为0.021%，公式2和公式3的系数预测值较校正值平均低估0.381%，FAO推荐值与校正值相差最大，平均低估计2.384%，特别是在福山，更是低估4.921%。就单个站点而言，福山和济南的系数预测结果较好，福山的系数预测值与校正值的差异在-0.501%～-0.141%，济南的系数预测值与校正值的差异在-0.536%～0.184%。莒县的系数预测效果较差，系数预测值与校正值的差异在-0.827%～1.003%。

由图（c）可以看出，由公式2、公式3和公式4预测得到的系数+在福山、济南和莒县的预测效果相类似；公式1在福山、济南与其他三个公式的预测结果类似，但公式1在莒县明显高于其他三个公式的预测值，平均高估0.6730%。公式1预测得到的系数+与校正值最为接近，二者的平均相差仅为0.022%，公式2、公式3和公式4的预测得到的系数+与校正值平均相差-0.381%，FAO推荐值与校正值相差最大，平均高估计4.279%，特别是在济南，更是高估计5.753%。就单个站点而言，各预测公式在福山的预测效果最好，预测值与校正值的差异在-0.052%～0.046%，平均-0.027%，在济南的预测值与校正值的差异在-1.137%～-0.417%，在莒县的预测值和校正值的差异在-0.673%～1.157%。

总的来看，FAO推荐值与校正值差异最大，系数以高估为主，系数以低估为主，系数+和校正值的差异最小，无论参数还是，都以济南和福山的预测效果最好，莒县预测效果最差。

2.2 Rs预测值与实测值比较

表 3 不同参数化方法预测的Rs与实测值的决定系数R2

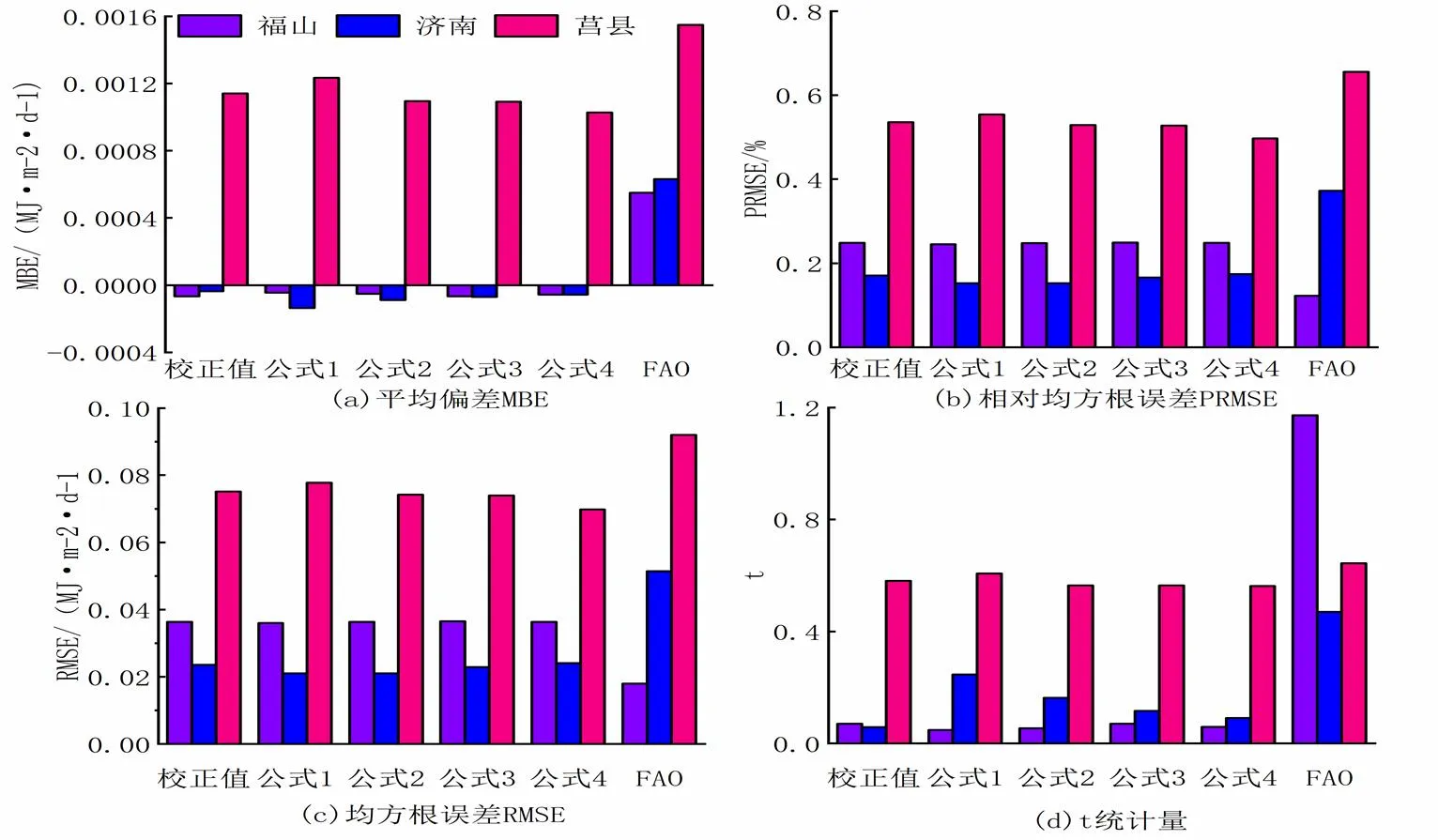
图 2 不同参数化方法预测的Rs与实测值比较的评价指标

表2是不同参数化方法预测的R与实测值的决定系数表，从表中可以看出，FAO的推荐值在三个站点的预测值与实测值的决定系数最小，精度最低。就单个站点而言，在福山五种参数化方法预测的2在0.9491～0.9561之间（表2），其中公式1、公式2、公式3和公式4的2与校正参数2几乎相同，FAO推荐值的2最小，精度最低。根据预测R与实测值计算的图2（a）,在福山以公式1最低，为-4.5×10-5MJ/(m2/d) ,其次是公式2和公式3，分别为-6.7×10-5和-5.2×10-5MJ/(m2/d)，且除了FAO推荐值为高估外，其他四个参数化公式均为低估。根据的结果分析图2（c），以FAO推荐值的最小，最小值为0.017937 MJ/(m2/d)，其他四个参数化公式几乎相同，并且与校正值的数值相当，公式1为0.036 MJ/(m2/d)，公式2为0.036 MJ/(m2/d)，公式3为0.037 MJ/(m2/d)，公式4为0.036 MJ/(m2/d)。根据的结果分析图2（b），公式1是24.54%，公式2是24.77%，公式3是24.92%，公式4是24.81%，四个参数化公式数值几乎相同，并且和校正值的也几乎相同。统计参量公式，四个参数化公式和校正值的数据大致相同，均远低于FAO的推荐值。

可见对于福山站点而言，虽然不同的评价指标得出的结论略有差异，但是以校正值为依据，公式1、公式2、公式3、公式4均与校正值接近，FAO推荐值与校正值的偏差较大，精度较低。总的来看公式1对于福山站2较大，较小，与校正值的数据相差不大，精度较高，表明福山站利用海拔和经度就能很好的估算A-P参数。

对于济南站点，各种参数化方法预测的2在0.9112～0.9116之间（表2），可以看出，各种参数化方法的2与校正参数的2几乎相同，而FAO推荐值预测的2最小。根据预测的R值与实测值计算的(图2a),公式1精度最低，为-1.4×10-4MJ/(m2/d)，其次是公式2和公式3，分别为-9.0×10-5、-7.0×10-5MJ/(m2/d)。从图中可以看出，济南的均小于0，说明不同参数化方法的预测结果均低于实测值。根据结果（图2c）,不同参数化方法的结果均非常接近，其中，以公式1预测的最小，为0.021 MJ/(m2/d)，与校正参数预测的较为接近的是公式4，均为0.024 MJ/(m2/d)，FAO的精度最低，其为0.051 MJ/(m2/d)。从上来看（图2b），公式1和公式2最低，其值均为15.23%，不同的参数化方法预测的与校正参数的相差不大，其中，校正参数的为17.05%，最高的为公式4，其值为17.41%，FAO的精度最低，其值达37.27%，远远高于其他参数化方法与校正参数。图2d的检验显示，在济南站不同的参数化方法包括FAO对应的值均不大，表明预测值与实测值的差异均不显著，其中，校正参数对应的值最小，为0.058，与校正参数最为接近的是公式4，其对应的值为0.091。

总体来看，不同的评价指标在济南站表现趋势大体一致，即公式1在该站点预测的精度最高，可见，在济南站用海拔和经度可以很好的估算A-P参数。

莒县站点各种参数化方法预测的2在0.9358～0.9397之间（表2），其中公式1、公式2、公式3和公式4的2与校正参数2几乎相同，FAO推荐值预测的2最小，为0.9358，精度最低。根据，在莒县公式4的最小，为0.001026885 MJ/(m2/d)，其次是公式3和公式2，分别是0.001091239 MJ/(m2/d)，0.001094568 MJ/(m2/d)，FAO推荐值的E最大，为0.001550169 MJ/(m2/d)，且参数化公式预测的结果都是高估。根据RMSE的结果分析图2（c），公式4的RMSE最小，为0.069779021 MJ/(m2/d)，其次是公式3和公式2，分别是0.073976317 MJ/(m2/d)，0.074193418 MJ/(m2/d)，FAO推荐值的最大。就而言，仍是公式4最小，为49.73%，其次是公式3和公式2，分别为52.72%、52.87%，以FAO推荐值最大，比公式1偏大15.85%。就统计参量而言，仍然是公式4最小，预测值与实测值无显著差异，其次是公式3和公式2，FAO推荐值最大。

总的来说、、、统计参量在莒县得出的结论完全一致，以公式1预测效果最好、精度最高，其次是公式3和公式2，FAO推荐值的预测效果偏差较大，精度较低。因此在莒县站点用经度和海拔来估算A-P参数效果最好。

3 讨论

基于日照的太阳辐射（A-P）模型的应用经常受参数校正的限制，在没有太阳辐射实测数据的站点，增加其参数的可用性是克服这一问题的主要方法。国内外很多研究者对A-P模型的参数进行校正[6,12-17]，但是利用容易获取的变量进行参数的预测研究较少，本研究利用容易获取的站点信息（海拔、经纬度、平均温度）等作为自变量建立参数预测模型。前人研究中建立的参数模型很少使用单一变量[18]，大多使用两个或两个以上的变量或者较多变量进行组合来构建参数模型，这无疑增加了模型的复杂性，其精度提高不多。本研究利用这些站点的地理位置信息作为自变量构建参数模型，其结构形式简单，预测结果精度较高，可以为山东省太阳辐射的准确估算提供参考依据。

本研究依据A-P公式参数与地理位置和平均温度的相关关系构建了参数预测模型，其结构形式简单，模型自变量容易获取，山东省三个站点FAO推荐值与校正值差异最大，系数以高估为主，系数以低估为主，系数+和校正值的差异最小。

参数，参数化预测结果和R的预测结果并不完全一致，这一结果与李曼曼等人的研究结果类似，参数，参数化预测结果表明：福山参数化预测的效果最好，预测值与校正值的差异在0.089%～0.449%，平均0.334%；济南的参数化预测效果其次，预测值与校正值的差异在-0.601%～0.119%，平均-0.308%；莒163邮箱县的预测化效果最差，预测值与校正值的差异在-1.676%～0.154%，平均-0.326%。但根据R预测值和实测值的比较后，却是莒县居中，济南最差，福山最好的这一结论保持不变，这可能是因为R的预测精度对A-P公式参数的估算公式要求不高导致的。

尽管不同的参数化方法在不同的站点估算R的精度有所差异，但是参数化方法的预测结果远好于FAO推荐值预测效果，且与校正参数预测效果相当，因此，本文所使用的参数化方法在山东省具有较好的适用性，可以在无实测资料的地区直接使用。

4 结论

本研究基于山东省3个站点（福州、济南、莒县）1992-2016年的气象和辐射观测资料，得到了站点多年的校正参数并构建了多种参数化方法，其结构形式简单，预测结果精度较高，可以为山东省太阳辐射的准确估算提供参考依据。本研究得出以下结论：

（1）不同参数化方法的预测精度随站点的不同而有所差异，总体上是以公式1（=5.43742×10-4+0.149=0.00964×-0.62367）效果最好。而FAO推荐值的预测总体来看无论是与校正值的接近程度，还是预测的评价指标的数值大小都是效果最差的。因此，在山东省可以用海拔和经度来估算A-P公式参数，从而进行太阳辐射的准确估算；

（2）参数、的预测结果好坏并没有完全体现在评价指标的好坏上，因此，在评价参数或者以及参数化公式的好坏时应以与校正值相比较为主，以评价指标为辅。

[1] Allen RG, Perreira LS, Raes D,. Crop evapotranspiration: guidelines for computing crop water requirements [M]. Rome: FAO,1998:56

[2] Liu XY, Xu YL, Zhong XL,. Assessing models for parameters of the Ångström–Prescott formula in China [J]. Applied Energy, 2012,96:327-338

[3] Yin YH,Wu SH, Du Z,. Radiation calibration of FAO56 Penman- Monteith model to estimate reference crop evapotranspiration in China [J]. Agricultural Water Management, 2008,95:77-84

[4] 胡庆芳,杨大文,王银堂,等.Angstrom公式参数对ET0的影响及FAO建议值适用性评价[J].水科学进展,2010,21(5):644-652

[5] 贺兴宏,管瑶.ET0计算中Angstrom –Prescott系数的取值[J].人民黄河,2012,34(9):91-94

[6] Liu XY, Mei XR, Li YZ,. Variation in reference crop evapotranspiration caused by the Ångström- Prescott coefficient: Locally calibrated versus the FAO recommended [J]. Agricultural Water Management, 2009,96:1137-1145

[7] 李曼曼,梅旭荣,钟秀丽,等.云南省Ångström-Prescott辐射模型的参数化研究[J].农业工程学报,2012,28(6):100-105

[8] 彭世彰,徐俊增,丁加丽,等.as和bs取值对参考作物蒸发蒸腾量计算结果的影响[J].灌溉排水学报,2006,25(3):5-8

[9] Allen RG, Pereira LS, Raes D,. Crop evapotranspiration –Guidelines for computing crop water requirements–FAO Irrigation and drainage paper 56 [R]. Rome: Food and Agriculture Organization of the United Nations, 1998

[10] Podestá GP, Núñez L, Villanueva CA,. Estimating daily solar radiation in the Argentine Pampas [J]. Agr Forest Meteorol, 2004,123(1/2):41-53

[11] Liu XY, Mei XR, Li YZ,. Choice of the Ångström-Prescott coefficients: Are time-dependent ones better than fixed ones in modeling global solar irradiance [J]. Energ Convers Manage, 2010,51(12):2565-2574

[12] Liu XY, Li YZ, Zhong XL,. Towards increasing availability of the Ångström–Prescott radiation parameters across China: Spatial trend and modeling [J]. Energy Conversion and Management, 2014,87:975-989

[13] Rietveld MR. A new method for estimating the regression coefficients in the formula relating solar radiation to sunshine [J]. Agric Meteorol, 1978,19:243-252

[14] Frére M, Rijks JQ, Rea J. Estudio agroclimatologico de la zona andina, Informetecnico [M]. Rome: FAO, 1978.

[15] Gopinathan KK. A general formula for computing the coefficients of the correlation connecting global solar radiation to sunshine duration [J]. Solar Energy, 1988,41:499-502

[16] Gopinathan KK. A simple method for predicting global solar radiation on a horizontal surface [J]. Solar Wind Technol 1988,5:581-583

[17] Zhou J, Wu Y, Yan G. General formula for estimation of monthly average daily global solar radiation in China [J]. Energy Convers Manage, 2005,46:257-268

[18] Liu XY, Mei XR, Li YZ,Calibration of the Ångström–Prescott coefficients (a, b) under different time-scales and their impacts in estimating global solar radiation in the Yellow River basin [J]. Agric.For. Meteorol., 2009,149:697-710

The Parametric Optimization of the Ångström-Prescott Solar Radiation Model in Shandong Province

TIAN Xiao-xu1,2, TIAN Hui2, ZHANG Peng2, LIU Fu-sheng2, ZHANG Qian1,2*

1.453000,2.271018,

The Ångström- Prescott model is an optimal solar radiation (R) model based on sunlight, but its application is often limited due to the lack of model parameters. In order to obtain the accurate model parameters of Shandong Province, the angstron-Prescott formula was used to calculate the solar radiation values at three stations (Fushan, Jinan and Juxian) in Shandong Province, using the recommended FAO values and four parameterized equations fitted according to the data of geographical location and annual average temperature. The results were compared with the measured values and the predicted values of the correction parameters. The results show that: (1) Among the three stations, the estimation effect of fushan parameter model is the best, Ju County is the second, and Ji 'nan is the worst. The coefficient of determination (2) of Fushan, Juxian and Jinan are in the range of 0.9559 ～ 0.9661, 0.9358 ～ 0.9397 and 0.9083 ～ 0.9115, respectively. However, the coefficient of determination (2) are all above 0.9. The correlation betweenRpredicted by different parameterization methods and measured values is high. (2) Formula 1 has the best effect in estimating the solar radiation value. The mean deviation (), the root mean square error () and the relative root mean square error () of the formula are between -4.54×10-5～ 1.23×10-3MJ/(m2·d), 0.021 ～ 0.078 MJ/(m2·d) and 15.23% ～ 55.40%, respectively. And the correction value are close, and the estimation accuracy of FAO recommended value is low, which is far lower than formula 1. Therefore, formula 1 (=5.43742×10-4+ 0.149=0.00964×-0.62367) by altitude and longitude can be used to accurately predict the solar radiation in Shandong Province.

Sun radition;model; parametric optimization

S161.1

1000-2324(2021)06-0942-07

2021-08-26

2021-09-12

中国农业科学院基本科研业务费项目(FIRI2016-25-01);国家重点研发计划课题(2018YFC0407703);山东省重大科技创新工程项目(2019JZZY010727);山东省重点研发计划重大科技创新工程项目(2019JZZY010710);山东省2017年度农业重大应用技术创新项目

田晓旭(2000-),男,本科在读,主要从事节水灌溉理论与技术研究. E-mail:tianxiaoxu2021@163.com

通讯作者:Author for correspondence. E-mail:zhangqian864@163.com