病态加权总体最小二乘的广义岭估计解法

翁烨，邵德盛

（ 1. 云南省地震局, 昆明 650200；2. 昆明理工大学 国土资源与工程学院, 昆明 650093 ）

0 引 言

最小二乘估计[1]理论和经典平差模型在大地测量数据解算以及工程领域中应用非常广泛，其中高斯-赫尔默特模型(GHM)为经典平差模型的常用形式[2]. 在实际应用中，坐标转换、大地测量反演、控制网平差、精密单点定位(PPP)等平差模型中的系数矩阵也含有随机误差，经典的GHM模型扩展为带有随机系数矩阵的变量误差模型[3]. 基于这种模型的解算，ADCOCK[4]首次提出了观测向量和系数矩阵具有随机误差的整体最小二乘估计解法，也叫总体最小二乘法[4].

处理病态总体最小二乘法问题的常用方法有截断奇异值法[5]、岭估计法[6-7]、正则化法[8]以及c-K法[9]等. 对于总体最小二乘法岭估计的解算方法主要在于岭参数的选取，其中岭参数的选取方法有：岭迹法[10]、L-曲线法[11]、U-曲线法[12]以及广义交叉检核法[13]等.在等权条件下总体最小二乘法的解算通常采用正则化方法研究的迭代式，迭代方法较为复杂，计算量偏大. 针对这种问题，王乐洋等[14]推导了病态加权总体最小二乘法平差的岭估计解式以及精度评定方法，对多种选取岭参数方法进行了对比分析. 基于此，本文考虑将病态加权总体最小二乘法中的岭估计解换成广义岭估计解，通过传统平差模型推导了未知参数的求解公式，利用协方差传播率导出参数解的方差-协方差矩阵、广义岭参数矩阵K中对角线元素ki(i=1,2,···,m)的迭代解式和均方误差.

1 加权总体最小二乘的广义岭估计模型

经典线性模型为

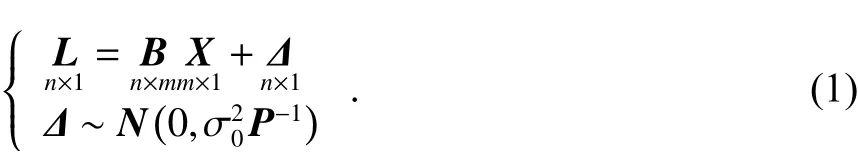
式中：L为观测向量；B为设计矩阵且R(B)=m；X为未 知参 数向 量； Δ 是 随 机 向 量 误 差；P是 权 矩 阵；Σ=σ2P-1是 协方差矩阵； σ2为单位权方差. 设参数的估值为观测值误差Δ的估计值为观测值的个数为n个，未知参数估计值的个数为m个，总体最小二乘在考虑观测向量的误差之外还要考虑系数矩阵的误差，设EB为系数矩阵B的误差向量矩阵，即B=B0+EB，因此经典线性模型扩展为变量误差(EIV)模型[1]

式中：eL∈Rn×1、EB∈Rn×m是观测向量L0和设计矩阵B0的误差矩阵，随机模型为

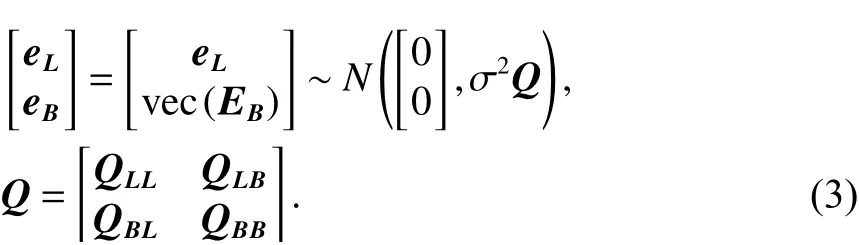
式中：Q为 (nm+n)×(nm+n) 阶 分块对角矩阵；vec(·)为矩阵的拉直运算，这里表示矩阵按行拉直得到的列向量；Q为观测值和系数矩阵元素之间的协因数矩阵为n×n阶 方阵，为nm×nm阶方阵. 将式(2)展开并且舍去二次项，得

令

加权总体最小二乘准则为

由于eB是EB通过行拉直所得到的列向量，排列顺序由左至右，根据式(5)的模型即有准则

在系数矩阵B病态时，矩阵存在的复共线性导致法矩阵的求逆变得极不稳定，王乐洋等[14]引入岭参数k，利用岭估计的优点来处理加权总体最小二乘的病态性问题. 但是岭估计的改进方法对于所有的参数无区别统一添加岭参数影响，对一部分参数估计的改进效果不明显. 在考虑广义岭估计的基础上，根据Tikhonov正则化原理[15]，得到式(5)的总体最小二乘广义岭估计准则为

tr(*) 表示求矩阵的迹，K=diag{k1,k2,···,km} ，结合式(5)和式(7)的模型准则，通过建立拉格朗日目标函数，分别对其求一阶偏导数，可以得到加权总体最小二乘的广义岭估计解为

下面借鉴文献[14]中求协因数矩阵的方法求Q¯ ，方法如下，由V=eL-EBX0，e=L0+B0X0可以得

D和G的表达式为

G矩阵是由eL矩阵和EB矩阵组成的增广矩阵，列向量 v ec(G) 中的所有元素eL1,···,eLn,EB1,1,···,EBn,m之间的互协因数及协因数组成的矩阵为：

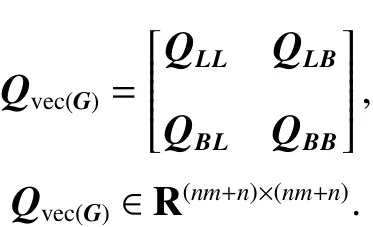
从(3)式中协因数Q得 到有Qvec(G)=Q，因此根据协因数传播率可以得到

2 广义岭参数ki的确定

2.1 岭参数的确定——L-曲线法

在1970年Mille首先采用L-曲线法求解病态方程，其后Hansen[16]又对该方法作了深入研究，L-曲线法是一种在均方误差有意义下的有偏估计算法，根据Tikhonov正则化原理，依据岭估计的估计准则可以表示为

式中： ‖ *‖ 为欧式2-范数； Ω (X) 是稳定泛函；式(11)在最小二乘估计准则基础上添加了kXTX项，由于这一项的参与，法方程的病态性得到了抑制，(BTB+kXTX)求逆变得正常起来，所以相比较最小二乘估计可以得到更加可靠的估计值. 岭估计结果优于最小二乘估计的原因就在于岭参数k，若选择不同的岭参数，得到的估计结果就会有所不同，所以岭参数的选取也至关重要，接下来介绍关于岭参数的选取方法之一L-曲线法.都是岭参数k的函数，选择不同的岭参数，以为 横坐标，以为纵坐标画图，得到许多点再利用多点曲线拟合的方式拟合出一条曲线，因为该曲线通常形状都像“L”，所以称为L-曲线.L-曲线的关键就在于选择曲线上曲率最大的那个点，其对应的岭参数即为所求. 接下来以对数形式推导式如下[11]：

令

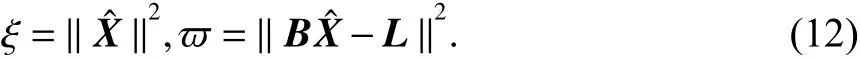
两边取其对数形式，得出

则L-曲线是由许多点 ( ξ/2,ϖ/2) 拟合成的曲线，用 ξ′,ξ′′,ϖ′,ϖ′′分别代表 ξ 和 ϖ 的一阶和二阶导数，所以 ξ ,ϖ,ξ′,ξ′′,ϖ′,ϖ′′均是岭参数k的函数，那么，在L-曲线上的点的曲率 η 的计算式为

关于 ξ′、ξ′′、ϖ′、ϖ′′的计算式可以参考文献[4-5]，对式(14)求取最大值，得到最大曲率 ηmax， ηmax所对应的点的岭参数即为所求，这样就定位出L-曲线上曲率最大的点.

从式(11)可以看出，在应用L-曲线法选择岭参数的合理性在于平衡数据拟合度部分和解部分这种平衡是通过岭参数来实现的，需要指出的是，用L-曲线法求得的岭参数不是最优选择，只是近似最优. 以上的推导过程是在权矩阵为单位阵的时候推导的，如果权矩阵不是单位矩阵，由于其都是正定型矩阵，可以先将权矩阵进行单位化，同理可以计算出L-曲线方法.

2.2 广义岭参数 ki 的确定

式中：J为正交方阵，是特征向量矩阵； Λ 是特征值对角方阵， Λ =diag{λ1,λ2,···,λm} ， 按照λ1≥λ2≥···≥λm降序排列；Z=B0J， α =JTx为典则参数. 式(5)模型的典则形式为

再根据协方差传播率，式(8)可以得到其协因数矩阵为

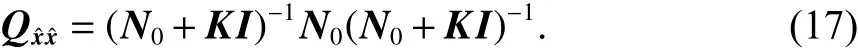
均方误差的定义为

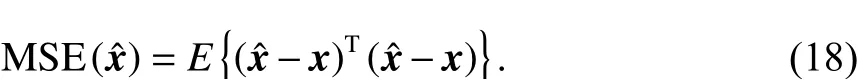
将式(8)带入到式(18)中，得到参数改正数估计值的均方误差为

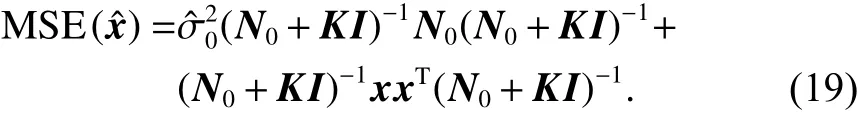
可由驻点求得满足均方误差最小化情况下，广义岭估计的岭参数为

根据式(22)确定的ki可 使 M SE(xˆ)=min ，但由于未知，因此无法由式(22)直接得到K中的每一个岭参数值，可用迭代法求得：

3)最后按照式

由式(22)可知，当m个广义岭参数相等且为一常数，即k1=k2=···=km=k时，就退化成岭估计，广义岭估计相比较岭估计的不同之处在于通过对法方程系数阵的主对角元素增加不同的k值来改善其病态性，而岭估计是在于法方程系数矩阵的主对角线元素上加上相同的常数k来达到改善病态性的目的. 广义岭估计是有偏的最小二乘的线性组合估计值，其主要作用在于使得引入的偏差值小于最小二乘估计的方差值，从而达到提高参数的估计精度. 岭估计是对最小二乘估计的改进，而广义岭估计是对岭估计的改进，不过广义岭估计与岭估计有着相同的性质.

3 算例及分析

采用文献[17-18]中的数值算例，在文献[14]算例的基础上进行改化，含有5个未知数，病态设计矩阵和观测向量的真值如下所示[16-17]：

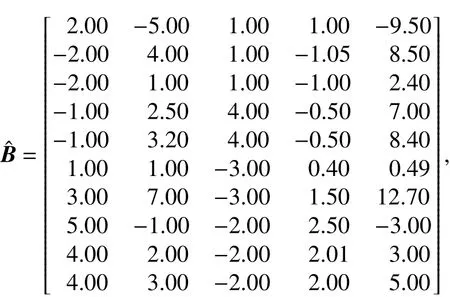
0=[0.8，0.8，0.8，0.8，0.8]T. 分别对观测值真值和设计矩阵真值添加模拟误差eL和eB，其是 设计矩阵B中的误差向量矩阵按行拉直后得到的列向量元素矩阵. 法矩阵N=B0TB0的条件数为cond(N)=2.084 × 104，严重病态性. 这里假设Pvec(EB)矩阵是一个对角线元素为0.5，其他元素为0.2的方阵，且Pvec(EB)∈R50×50. 为了显示本文解法的可行性和优越性，设计了多个方案.

方案一：不考虑设计矩阵B误差的最小二乘解法；

方案二：考虑设计矩阵B误差的总体最小二乘解法；

方案三：不考虑设计矩阵B误差的岭估计解法；岭参数采用L-曲线法求得；

方案四：考虑设计矩阵B误差的总体最小二乘岭估计解法；岭参数采用L-曲线法求得；

方案五：不考虑设计矩阵B误差的总体最小二乘广义岭估计解法；

方案六：考虑设计矩阵B误差的总体最小二乘广义岭估计解法.

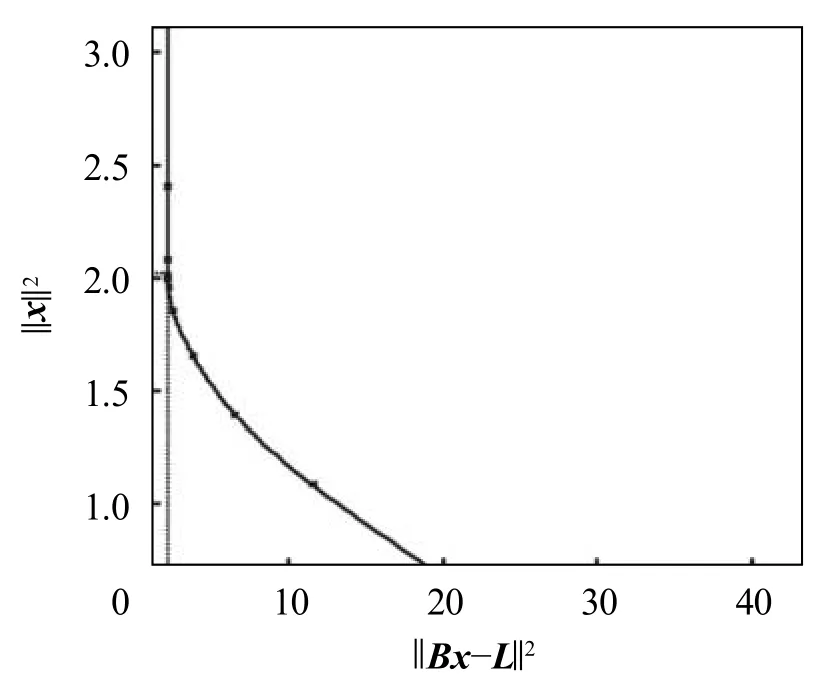
图1 方案三岭参数（L-曲线）

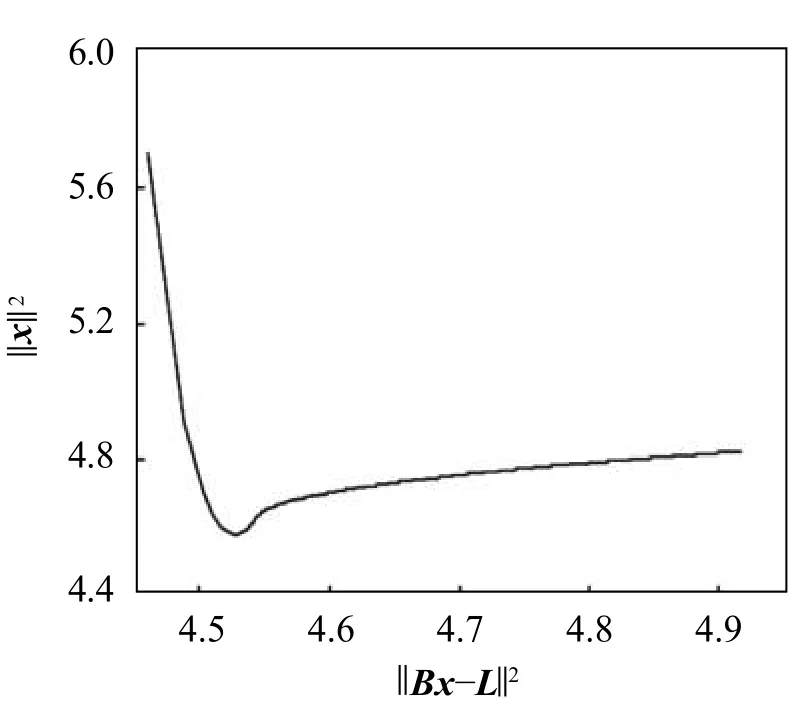
图2 方案四岭参数（L-曲线）

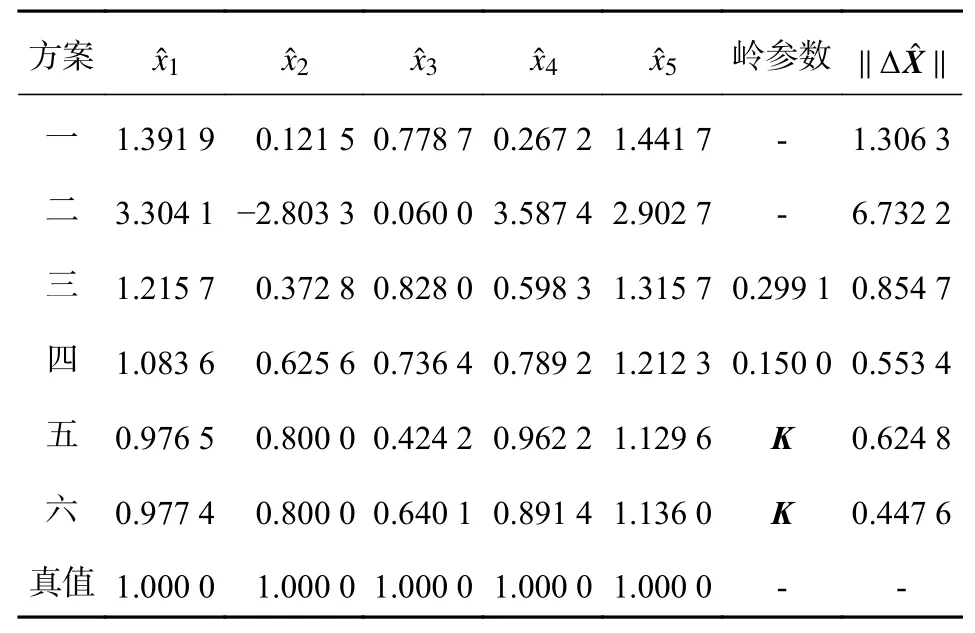
表1 不同方法的解算结果

通过计算对比分析，可以得出以下结论：

1)模型参数计算中，最小二乘的岭估计解优于普通的最小二乘解，更加贴近于真值，计算得到方案一和方案三的范数值分 别为1 .3063 和 0 .8547 .可见岭估计可以改善最小二乘估计.

2)总体最小二乘岭估计估计相比较总体最小二乘估计，差值范数更小，由表1可知方案二和方案四的值 分别为 6 .7322 和 0 .5534 .

总体最小二乘广义岭估计优于总体最小二乘岭估计，其差值范数更小，原因在于广义岭估计的岭参数选取更加全面，更能削弱系数矩阵的病态性. 但是在不考虑设计矩阵误差的情况下，考虑设计矩阵误差的岭估计解优于普通最小二乘的广义岭估计解. 可以看出，设计矩阵自身的误差对参数估计影响较大，因此，考虑设计矩阵的误差项不可避免.

3)根据式(17)得出本文方法的协因数矩阵如表2所示. 方案六在考虑设计矩阵误差的情况比方案五得出的参数估计值更加贴近于真值，方案五和方案六的差值范数分 别为 0 .6248 和 0 .4476 .

表2 方案六的协因数矩阵

4 结 语

EIV模型同时顾及了设计矩阵的误差项和观测向量的误差项，适用解法为总体最小二乘估计，总体最小二乘估计优于最小二乘估计. 但是系数矩阵存在复共线性时，一般的总体最小二乘估计也难以得到稳定的估计值，且估计值的均方误差也不理想，因此必须要针对设计矩阵的病态性进行处理. 在考虑设计矩阵自身误差项的基础上，对法方程系数矩阵添加改正项，借鉴广义岭估计的优势，推导出在病态加权下总体最小二乘的广义岭估计直接解法，广义岭参数采取迭代求解法，优于总体最小二乘的岭估计解，在处理病态加权的变量含误差模型有一定的借鉴作用.