高校智能快递柜选址研究及应用
雷鸿霞,范雯雯,刘娜翠
(福建农林大学 交通与土木工程学院,福建 福州 350108)
0 引言
近年来,电子商务行业发展迅速,高校学生逐渐成为网络购物的主力军,其消费规模逐年加大。我国大部分高校学生都是在校园内外一些固定站点进行快递取件,在“双十一”等网购高峰期,取件点处经常会出现排长队现象,且伴随着快递件取错、丢失等情况发生,此种现象催生了智能快递柜。智能快递柜是一柜一物个人制快递存取,并配备有监控设备,能够具有针对性地解决快递件的丢失、错领问题,提高快递件存放的安全性。同时,快递柜提供24h自助服务,可以随时取件,对于大学生来说,能够在下课之余有充足的时间灵活取件。智能快递柜的合理布设能够有效地解决高校末端物流环节中存在的问题。
智能快递柜近几年主要应用于小区住所和企事业单位等场地,而高校内的智能快递柜数量不多,有很大的发展空间。智能快递柜的选址问题也引起了学者们的关注,李淑芳,等通过建立集合覆盖模型为供应点设定最大服务距离,在尽量满足需求的同时建设最少的快递网点;施书彪,等将租金、配送和惩罚三个方面的成本最小化作为优化目标,提出了校园智能快递柜选址模型;刘程程,等利用K-mean法对选址区域进行分区,建立了智能快递柜备选址评估指标模型,通过层次分析法和模糊综合评价法确定备选址的位置。目前的选址研究已取得一定的成果,但将定量和定性方法相结合,考虑高校自身因素进行选址的研究还不够完善。因此,本文综合AHP法、古林法和集合覆盖法的优势,以福建农林大学旗山校区为例,进行智能快递柜选址研究,对智能快递柜进行最佳选址,使学生取件的需求得以最大程度的满足。
1 高校智能快递柜选址问题
在高校内,已知有M块空地可用于建设智能快递柜,选取其中m块为备选快递柜点。学校共有n个快递柜需求点,拟从m个备选点中选出p个点安置智能快递柜。根据快递柜选址的影响因素对M块空地进行评价并排序,确定m个备选快递柜点。已知快递柜的存储量和需求点的需求量是固定的,考虑智能快递柜建设总成本最小和客户满意度最大来确定最终智能快递柜选址位置。
问题假设:(1)不考虑区域内交通影响因素,设定所有网点的最大服务半经上限一致;(2)需求点的位置和需求量固定不变;(3)智能快递柜的建设固定成本相同;(4)备选快递柜点和需求点的距离采用两点间最短直线距离表示。
智能快递柜的建立,最重要的是让用户满意,取件花费的时间越短,客户的满意度越高。用户到快递柜的距离越短,取件就越方便。因此,在智能快递柜固定的服务半径内,以设立最少的覆盖点为目标,使所有的需求点都能够有至少一个设施点为其提供服务。因此,建立如下优化模型:


式中:x与y均为0-1变量,x=1表示在i点建立智能快递柜,x=0表示在i点不建立智能快递柜;y=1表示备选网点i到需求点j的折线距离在L内,y=0表示备选网点i到需求点j的折线距离在L外。q为需求点j的需求量;R为一组智能快递柜的存储量。d表示设施点i到需求点j的距离,L表示服务对象可接受的智能快递柜的投放距离,即设施点最大覆盖半径。
式(1)为模型的目标函数,表示快递柜的总数量最少。式(2)表示每一个需求点只能由一个快递柜网点提供服务。式(3)表示智能快递柜容量不能小于需求点的需求量。
2 问题的求解方法及步骤
智能快递柜选址较为复杂,难以完全采用定量的方法把问题简单归结为费用、效益或有效度进行研究。AHP法通过两两比较的方式确定层次中诸多因素的相对重要性,能够使复杂的问题简单化。智能快递柜选址点和影响因素多,且各个因素的度量单位不统一,因此利用AHP法计算快递柜选址各评价指标的权重(W),在此基础上,古林法可以对被评价的M块空地的相对重要性做出定量分析,从而得到备选快递柜点,使结果更加合理化。具体求解流程如图1所示。

图1 高校智能柜选址问题求解流程图
3 实例应用
福建农林大学旗山校区是近几年开始建设的新校区,学校周边两个快递驿站分别设置在校门外和校内的图书馆,校门外的快递驿站所存快递数量比图书馆多,学生主要从校外的取件点进行取件,但有时由于快递数量多,快递公司不同,学生们需要从校内外驿站分别取件后才能完成全部快递的取件任务,整个快递取件流程路线较长,过程较繁琐,所耗费的取件时间也较长。受新冠疫情影响,福建农林大学旗山校区实行半封闭制管理,给校区学生的快递取件带来了更多不便。为了最大程度地提高学生们的取件方便程度,改变现有传统取件模式,因此根据福建农林大学旗山校区的实际情况进行智能快递柜的最佳选址研究具有重要意义。
3.1 影响因素权重计算
对实地情况充分了解后,选取4个影响智能快递柜选址的主要因素:选址区域可用面积、选址区域日常人流量、选址区域成本、选址区域周边日快递平均需求量。
利用AHP法计算4个因素间的重要程度,即权重。选址区域可用面积、选址区域日常人流量、选址区域成本、选址区域周边日快递平均需求量分别对应编号B1、B2、B3、B4。根据专家评估,对各影响因素之间的重要性比较建立判断矩阵,见表1。
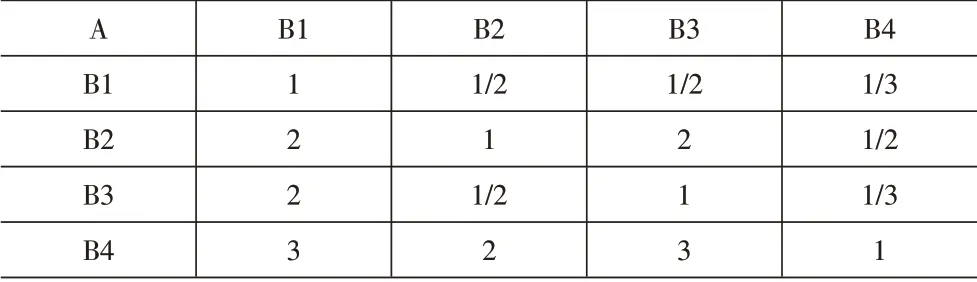
表1 判断矩阵
经过计算得到该判断矩阵的C.R.值为0.027,通过一致性检验。计算相对重要度W可得各评价指标的权重,见表2。

表2 各评价指标权重
3.2 备选点确定
选取福建农林大学旗山校区的南门、宿舍楼、操场、食堂、东门广场、图书馆、教学楼、北门8个地点为研究对象,分别记为P1、P2、P3、P4、P5、P6、P7、P8,地理位置如图2所示。
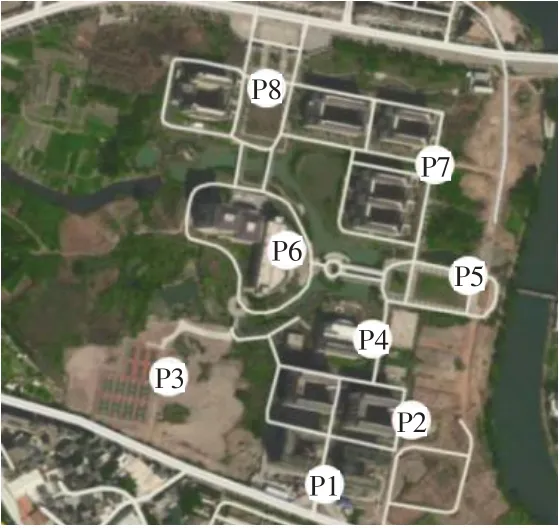
图2 快递柜候选点
据智能柜市场运作情况调研,对以上各候选点相关指标进行数据收集和预估,见表3。
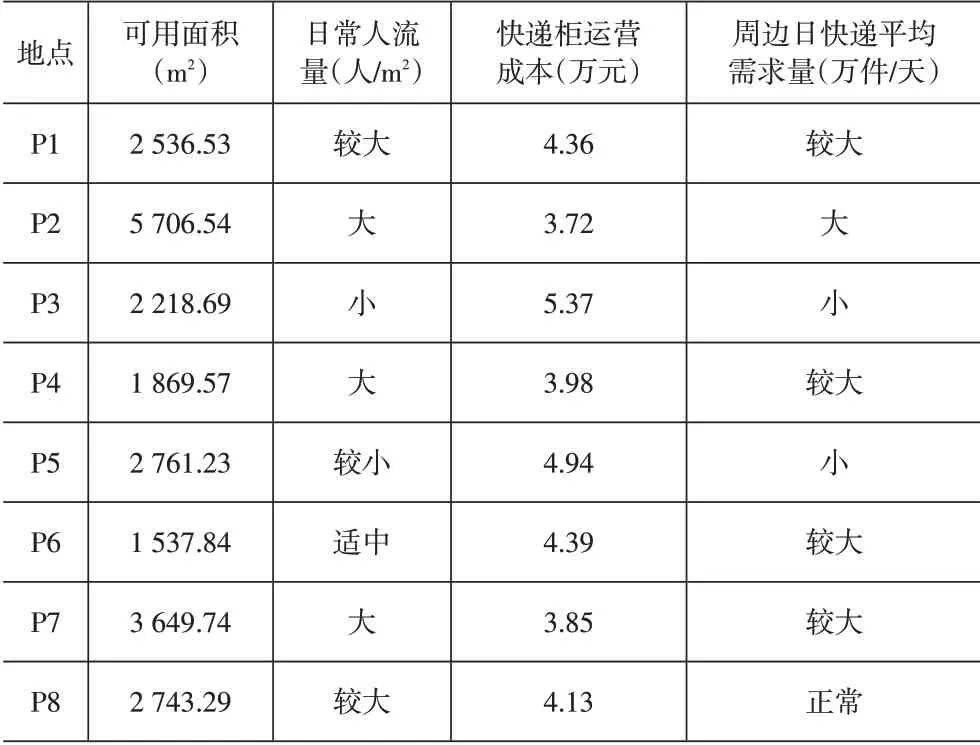
表3 选址区域各候选点指标数据
由于无法获取日常人流量与周边日快递平均需求量这两个指标的准确数据,故对此建立标度,以便后续计算,标度见表4。
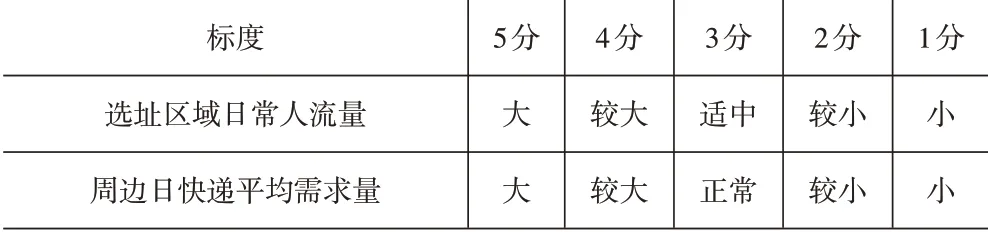
表4 评价标度
使用Python数据处理软件进行计算,计算所得关联矩阵见表5。
由表5可知,各候选点的综合评定值排序依次为P2、P7、P4、P1、P6、P8、P5、P3。点P5、P3评定值太低不予以考虑,因此确定点P2、P7、P4、P1、P6、P8为备选点。
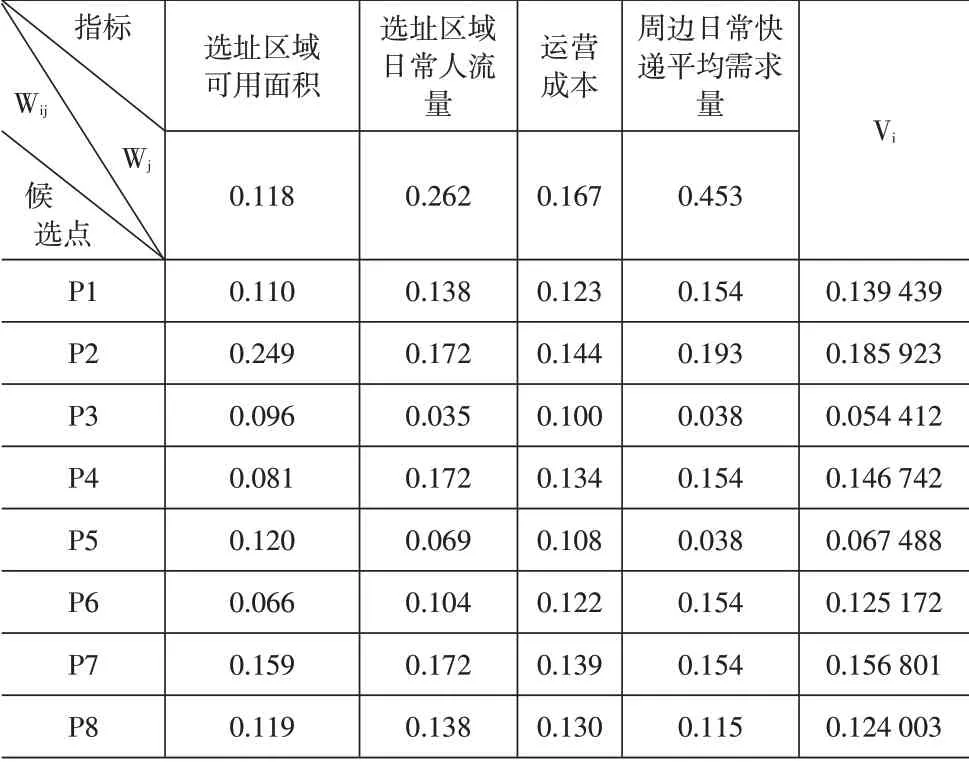
表5 关联矩阵表
3.3 快递柜位置确定
根据古林法计算结果可得,智能快递柜安置备选点为P1、P2、P4、P6、P7、P8。旗山校区内对智能快递柜的需求点有学生宿舍1、2、3、4号楼(分别用#1、#2、#3、#4表示),图书馆,实验1、2号楼,教学楼。根据学生问卷调查显示,80%的学生可接受智能快递柜的最大服务半径为300m左右,故将300m设置为集合覆盖模型中设施点的最大服务半径。假设一个智能快递柜的存储量为640件,快递柜备选点至需求点的距离见表6。

表6 快递柜备选点至需求点的距离
调查得知各需求点快递日需求量见表7。

表7 各需求点快递日需求量
结合式(1)-式(6),运用lingo 11.0计算得出智能快递柜的最终选址为P2、P6、P7。即在福建农林旗山校区内,设定辐射半径为300m的情况下,只需在点P2、P6、P7这三个地点分别安置数量为3组、1组、2组的智能快递柜,即可满足该校区内所有的智能快递柜取件需求。最终选址方案见表8。

表8 选址方案
3.4 结果分析
通过计算得到的智能快递柜最终选址点是在校区的宿舍楼、图书馆、教学楼这3处,并分别安置3组、1组、2组的智能快递柜即可满足整个校区学生的取件需求。宿舍区的取件需求最高,其次是教学区、图书馆,各个选址点处的快递柜数量能够适应所服务需求范围的取件需求密度,最大程度地满足对整个校区取件需求点的覆盖,能提高整体的取件效率和取件方便程度。
4 结语
为了有效提高高校快递取件的方便程度,解决传统取件模式带来的快递件错领、丢失及排队现象严重等问题,提出用层次分析法、古林法和集合覆盖理论相结合的方法对高校智能快递柜进行选址优化,结合福建农林大学旗山校区进行实例计算,结果证实研究所提出的方法能够实现高校内智能快递柜布局的最优化,提高高校“最后一公里”的服务质量。

