异质能量约束的集群学习节点选择机制

张富春，朱孔林,2

(1.北京邮电大学 人工智能学院，北京 100876；2.紫金山实验室，江苏 南京 211111)

0 引言

群体智能(Swarm Intelligence,SI)起源于对社会性昆虫，如蚂蚁、蜜蜂等的群体行为的研究，具有分布式和自组织性等特征[1]。群体中的个体基于环境状态而动，通过与环境的智能交互形成整个群体的智能。在机器学习领域，人们通过相关的机器学习算法让群体中的个体采取不同的行为，并根据从环境中获得的反馈来优化其个体行为，使得个体获得智能进而实现群体智能。未来的各种智能节点可能广泛分布于端边云各处，通过无线网络连接在一起，并通过一定的群体智能算法来实现群体智能。

集群学习[2](Swarm Learning,SL)作为一种分布式的机器学习具有群体智能的部分特征，它通过无线网络连接若干智能节点，以去中心化的方式来训练深度神经网络。典型的SL系统由各种智能节点以及连接各节点的无线网络组成。在实际的系统中，各个智能节点自主完成模型训练，并通过无线网络来共享模型参数。

本文主要关注这种分布式机器学习系统中的节点选择问题，即如何决定每一轮由哪些节点参与模型的训练才能使整体训练效率最高，同时还要保证每个节点的能量消耗不超过对应上限。之所以每一轮要选择部分节点参与训练，是因为这种分布式的机器学习系统中参与训练的节点数量达到一定规模后，再增加节点数量带来的整体收益增幅越来越小[3]。

SL系统的节点选择并非一个简单的问题。首先，系统中的节点受到能量限制，每个节点都有一个长期的能量上限。其次，由于SL系统中的节点所持有的数据集、物理硬件各不相同，不恰当的节点选择可能会对训练效果产生负面影响[4]。最后，SL系统中的各个节点通常是通过无线网络相互连接，而无线网络状态通常是时变的，因此需要考虑无线网络质量对模型参数传输的影响。

本文采用李雅普诺夫优化[5](Lyapunov Optimization)管理各节点的能量消耗以使总能耗不超过长期的能量上限，并结合组合多臂赌博机[6-12](Combinatorial Multi-Armed Bandit,CMAB)动态感知各节点的性能状况与无线网络状态，综合多种信息选择合适的节点组合参与模型训练。

1 相关工作

本节对相关工作进行分类和讨论，然后指出本文工作与它们的不同之处。与SL系统中的节点选择问题直接相关的文献极少，而与之高度相关的问题是联邦学习中的客户端节点选择问题，相关文献总结如下：

文献[13]使用节点反馈的信息(例如无线信道状态、算力资源以及与当前训练任务相关的数据资源的大小)来估计模型下载、更新和上传所需的时间，并设计了一种基于上述时间的算法，以在规定的时间内使尽可能多的节点参与模型训练，并将问题建模为0～1背包问题使用贪婪(greedy)算法求解。类似的文献[14]以CPU、内存和能量等的“资源效用函数”为约束，并基于线性回归对其进行预测。通过证明，其问题可以简化为经典的背包问题，并使用贪婪算法在每一轮中尽可能多地选择满足资源效用约束的节点来求解。

文献[15]考虑了节点的能量上限和无线信道条件。该工作采用了李雅普诺夫优化，定义虚拟能量队列来管理节点的能量消耗，并定义了基于节点的数据集大小和虚拟能量队列的效用函数。该工作定义的问题是在带宽限制的约束下最大化效用函数的优化。通过基于队列长度和信道增益的“选择优先级”来确定每一轮选择哪些节点。文献[16]也考虑了带宽限制的问题，并且更加关注无线资源分配问题，定义了节点的“经验损失函数”，并将其问题建模为带宽受限的随机优化问题。通过引入李雅普诺夫优化，将原问题转化为在线问题并在每一轮求解随机优化问题。

文献[17]考虑了训练时延、节点可用性和选择的公平性，设计了基于训练时延的奖励函数，在CMAB的理论框架下对问题进行转化并使用经典CMAB算法—UCB1[18]求解。文献[19]研究了节点选择的公平性对模型训练性能的影响，并定义了一个名为“模型交换时间”(Model Exchange Time)的指标，包含模型下载时间、训练时间和模型上传时间。最后设计了基于上下文CMAB的算法，以保证选择公平性为约束最小化“模型交换时间”。

本文的研究工作不同于上述文献。文献[15-16]主要关注无线资源分配问题，而这在SL系统中是不切实际的，因为无线资源相关的信息在实际SL系统中无法获取。文献[13-14]定义了类基于线性回归预测的指标来选择节点，而类似线性回归方法无法很好地反映相关指标的真实状态。与本文工作最相近的是文献[17-19]，虽然考虑了训练时延和选择的公平性，但忽略了节点的能量消耗。综上所述，现有的研究都没有考虑长期的异构能量约束下的节点选择问题。

2 系统描述与问题建模

2.1 系统描述

图1 集群学习系统Fig.1 Swarm learning system

在实际的SL系统整个训练过程前的初始化阶段中，所有节点均会参与一次模型训练以获取各个节点的初始性能信息。在之后的每一轮训练开始前，领导者节点基于各个节点的网络状态、历史训练时延以及能耗表现综合选择合适的节点组合参与本轮训练。

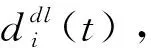
SL系统分为中间件和应用层[2]，中间件负责管理无线网络通信相关问题。然而，由于无线网络的时变特性，参数传输过程可能出现错误进而影响整体训练的效率。为解决这一问题，将Di(t)设置为一个上限Dmax。如果某节点因为网络问题导致模型传输失败，则将其对应的Di(t)设置为Dmax，同时在参数合并时忽略该节点，Dmax的值根据训练模型的不同由实际需要确定。

2.2 问题建模

(1)

(2)

式中，Ⅱ{·}为指示函数，即条件为真其值取1否则取0。约束条件(1)为长期的能耗约束，其含义为各个节点的总能耗不能超过其先验上限。约束条件(2)表示参与每个全局模型训练的节点数量均为k。

问题(P1)可以简化为一个标准的背包问题，其中各个节点的能量上限对应于背包的容量；节点每一轮的能耗对应于物品的重量，uj(t)是物品的价值，因此问题(P1)是一个NP难问题。此外，质量函数的具体值只有在节点实际进行模型训练后才能观察到。然而，领导者节点需要在实际的训练开始之前进行节点选择，而此时质量函数的实际值尚不可获取。因此，问题(P1)无法离线求得最优解。为了求解问题(P1)，本文在 CMAB 理论框架下将该离线问题转化为逐轮在线问题并求得次优解。

2.3 问题转化

采用CMAB理论的思路，将问题(P1)转化为在线形式。定义质量函数的“置信上界”如下：

(3)

式中，

(4)

s.t.(1),(2)

。

根据文献[21]，CMAB算法在经过数轮迭代后会倾向于选择某些特定的节点组合，使这些节点的能量快速耗尽而无法继续参与训练。因此，本文引入李雅普诺夫优化机制来平衡节点被选中的频率。定义节点i的能量赤字队列如下：

(5)

式中，[·]+=max{·,0}，Ⅱi,j(t)=Ⅱ{i∈Sj(t)}。T0为训练轮数的上界，实际系统中可将其设置为历史训练的最大轮数。初始的能量赤字队列Θi(t)为0，当某节点被频繁选中时，其对应的Θi(t)将快速增大，反之则Θi(t)将保持较小值。通过最小化被选中节点的总能量赤字队列，可间接控制各个节点被选中的频率。同时，通过最小化被选中节点的能量赤字队列也可以控制节点的能量消耗，使其不超过能量上限。根据文献[5]，约束条件(1)自然得到满足只需能量赤字队列保持稳定，即：

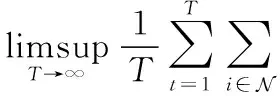
(6)

本文给出定理1证明上述陈述。

定理1若整个集群学习过程中的所有节点的能量赤字队列保持稳定，则长期能量约束(1)始终满足。

证：根据文献[5]中的定理2.5，若整个集群学习过程中的所有能量赤字队列Θi(t)保持稳定，则有：

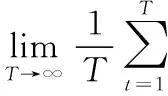
(7)

将CMAB与李雅普诺夫优化结合，重新定义节点的质量函数如下：

qi(t)=V·Di(t)+Θi(t)ci(t)。

(8)

qi(t)的估计值为：

(9)

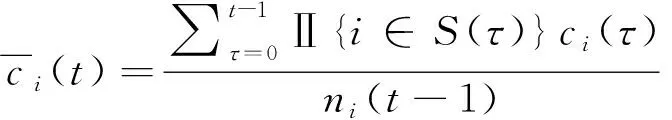
(10)

基于上述定义，给出问题的最终形式：

s.t.(6),(2)

。

问题(P3)可以通过对所有节点的质量函数值排序并选择其中最小的K个求解出相应的节点集合。

3 能量感知的节点选择算法

3.1 详细算法

为了求解问题(P3)，提出了能量感知的节点选择算法(Energy Aware Node Selection,EANS)。将问题建模为异质能量约束的 CMAB 问题，其中节点对应多臂赌博机的“臂(arm)”，训练时延对应“奖励(reward)”，选择节点对应选择arm。为了处理异质能量约束，将李雅普诺夫优化与 CMAB 算法结合，通过最小化本文定义的虚拟能量赤字队列并确保其保持稳定，使得各个节点的总能耗不超过其能量上限。

EANS算法由初始化和主循环2个阶段构成。在第1行所示的初始化阶段中，领导者节点选择所有节点进行一次模型训练并收集各节点反馈的时延Di(t)和能量消耗ci(t)，用以初始化算法。如第 3 行所示，此后的每一轮领导者节点对所有节点上一轮的质量函数值进行排序，选择上一轮质量函数值最小的K个节点参与本轮的模型训练。这K个节点按照质量函数值升序分成每k个一组，如图2所示。

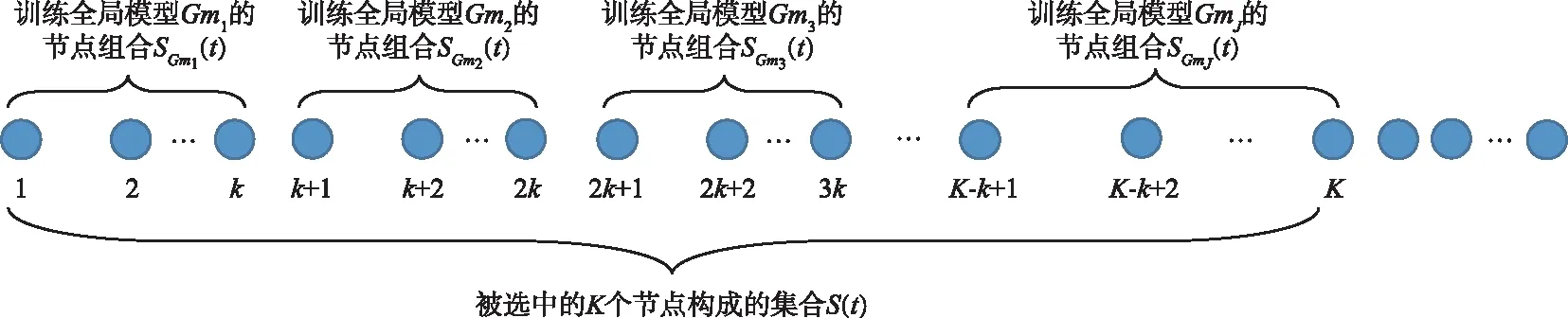
图2 节点组合的划分方式Fig.2 Assignment of node groups

完成节点选择后，第4行调用算法2分配节点组合至每个全局模型。之后各个被选中的节点在本地进行模型训练，并上传训练后的模型(第5行)。节点完成训练后领导者节点会对本轮被选中的节点的训练时延和能耗进行收集，并更新对应的质量函数(第6，7行)。

由于每个节点所持的数据不同，每个全局模型所需的数据也可能不同。因此，需要设计一个算法，尽可能将持有全局模型所需数据的节点分配给对应的模型。本文提出算法2来确定全局模型和节点组合之间的对应关系。

3.2 理论分析

证明图2所示的划分方式是问题(P3)的可行解，同时给出虚拟能量赤字队列的上界以证明虚拟能量赤字队列的稳定性。

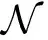
证：设任意一种将K个被选节点分为k个一组的序列为S′j(t),j=1,2,…,J。为描述方便，不妨设任意S′j(t)中的节点按其质量函数值升序排列，则有：

由于SGmj(t)序列按质量函数值升序得到，因此显然存在以下关系：

由S′j(t)序列的任意性可得出SGmj(t)序列是问题(P3)的一种可行解。定理2证毕。

在证明虚拟能量赤字队列的稳定性之前，需要介绍一个假设：

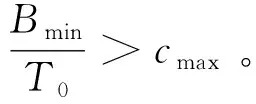
假设 1 的含义为节点有足够的能量参与全程SL的训练过程。有了上面的假设，给出式(6)的严格上界，如下所示：

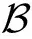
(11)

式中，

证：

首先，定义如下符号：

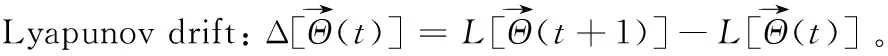
求解Lyapunov drift的上界：

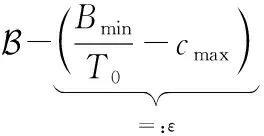
(12)

对式(12)两端从t=1,2,…,T求和，除以T再放缩可得：

(13)

对式(13)中的T取极限，两端除以ε即可得定理3。定理3证毕。

4 实验验证

4.1 实验设置

本文实验在一台搭载Intel Xeon E5 CPU、32 GB RAM、2 TB HDD、512 GB SSD和Ubuntu 16.04.1 LTS 操作系统的桌面服务器上进行。使用Flower[23]平台构建SL框架。采用Docker容器模拟了20个节点，各节点的能量上限1 300～1 600 J随机变化。使用扩展的手写数字分类数据集 EMNIST[24]进行模型训练。EMNIST 的数字部分包含10个类别的28 pixel×28 pixel灰度图像，训练集包含240 000条数据，测试集包含40 000条数据。本文将训练集中的240 000条数据和测试集中的 32 000条数据组合在一起，并将其分成 20 组作为20个节点的训练集。剩余的8 000条数据用作所有节点的测试集。

通过实验评估了EANS的能量赤字队列、总能量消耗、训练时延等指标。由于本文算法采用了CMAB框架，则对比算法也应该在CMAB的框架下，否则不具有可比性。因此本文与以下2种常见算法比较以评估EANS算法的性能。

(1) 随机算法Random：随机选择每一轮由哪K个节点参与训练；

(2) 文献[17]提出的用于联邦学习中客户端节点选择的CS-UCB-Q算法：中心服务器在fairness约束下选择延迟最小的节点(参见文献[17]中的不等式6)。

4.2 实验结果

图3 展示了能量赤字队列随轮次t的趋势。由图3可见，能量赤字队列先增加后减小，最后趋于稳定。此外，随着参数V的增加，能量赤字队列的上界也增加，这证明定理3是正确的。

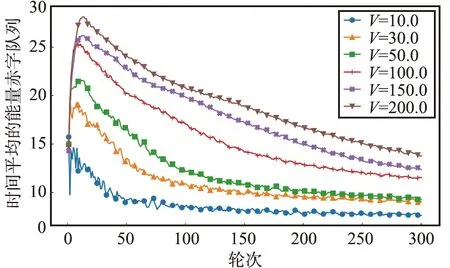
图3 能量赤字队列在不同V值下的趋势Fig.3 Trend of energy deficit queue vs round under different V

本文评估了EANS算法在不同情况下能量消耗的表现，并与CS-UCB-Q和Random进行了比较，如图4所示。由于CS-UCB-Q没有考虑能量的影响[17]，在不同的参数V设置下，其能量消耗接近随机算法Random，并且明显高于EANS算法。

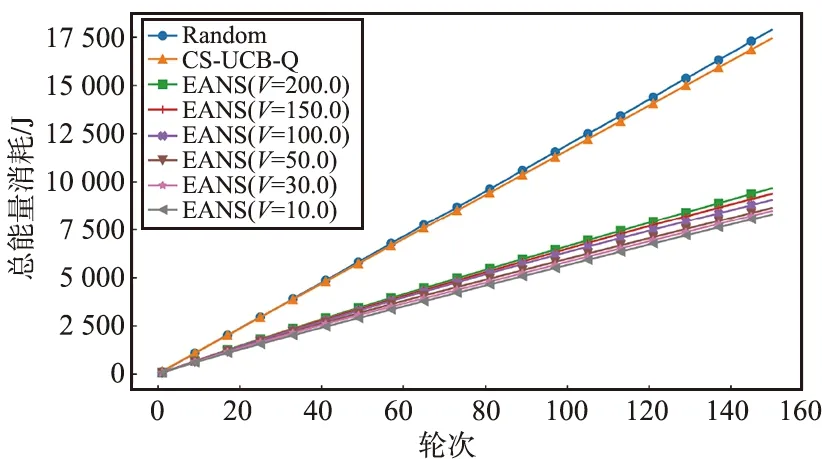
图4 几种算法的能量消耗趋势Fig.4 Trend of energy consumption of different algorithms vs round

由图4可以看出，当V=200时，EANS算法的能耗为CS-UCB-Q算法能耗的54.6%，而当V=10时，能耗仅为CS-UCB-Q的45.5%。与随机算法Random相比，EANS算法在V=200时能耗仅为Random能耗的54.0%，在V=10时为45.0%。

图5展示了EANS算法在不同情况下训练时延的表现，以及与CS-UCB-Q和Random的对比。由于 CS-UCB-Q更关注训练时延而EANS不仅考虑了训练时延还考虑了能量消耗，需要在二者中做出权衡，因此CS-UCB-Q的总训练时延比EANS的要小。

图5 几种算法的训练时延在不同V值下的趋势Fig.5 Trend of training delay of different algorithms vs round under different V

由图5可以看出，EANS算法的总训练时延比参数V=10时的CS-UCB-Q多44%，而当参数V=200时，EANS算法的总训练时延仅比CS-UCB-Q多19%。同样地，由于EANS算法在参数V较小时更关注能量消耗的影响，因此EANS的训练时延比随机算法Random大，而当参数V变大时，EANS算法的训练时延表现则优于随机算法Random。

5 结束语

本文提出一种新的用于集群学习的节点选择算法——EANS算法，该算法考虑了无线网络质量对集群学习系统整体训练效率的影响，着重关注了模型训练时延和能量消耗。采用CMAB理论结合李雅普诺夫优化的方法在无需节点详细性能信息的情况下为模型训练选择次优的节点组合，在保证整体训练效率的同时控制节点能量消耗不超过其能量上限。

从实验结果可以看出，EANS算法可达到接近最优解的性能。在能耗方面，当V=200时，EANS的能耗为CS-UCB-Q的54.6%，而当V=10时仅为CS-UCB-Q的45.5%。与随机算法Random相比，EANS算法的能耗是随机算法的54.0%而V=10时仅为其45.0%。

未来的工作，将考虑在节点选择的目标函数中引入模型的准确度，更加真实地反映节点的性能。同时，考虑对节点的能耗进行更加精确的建模，以使目标函数能更加全面地反映节点的真实状态。