看似寻常最奇崛， 成如容易却艰辛

倪钰皓

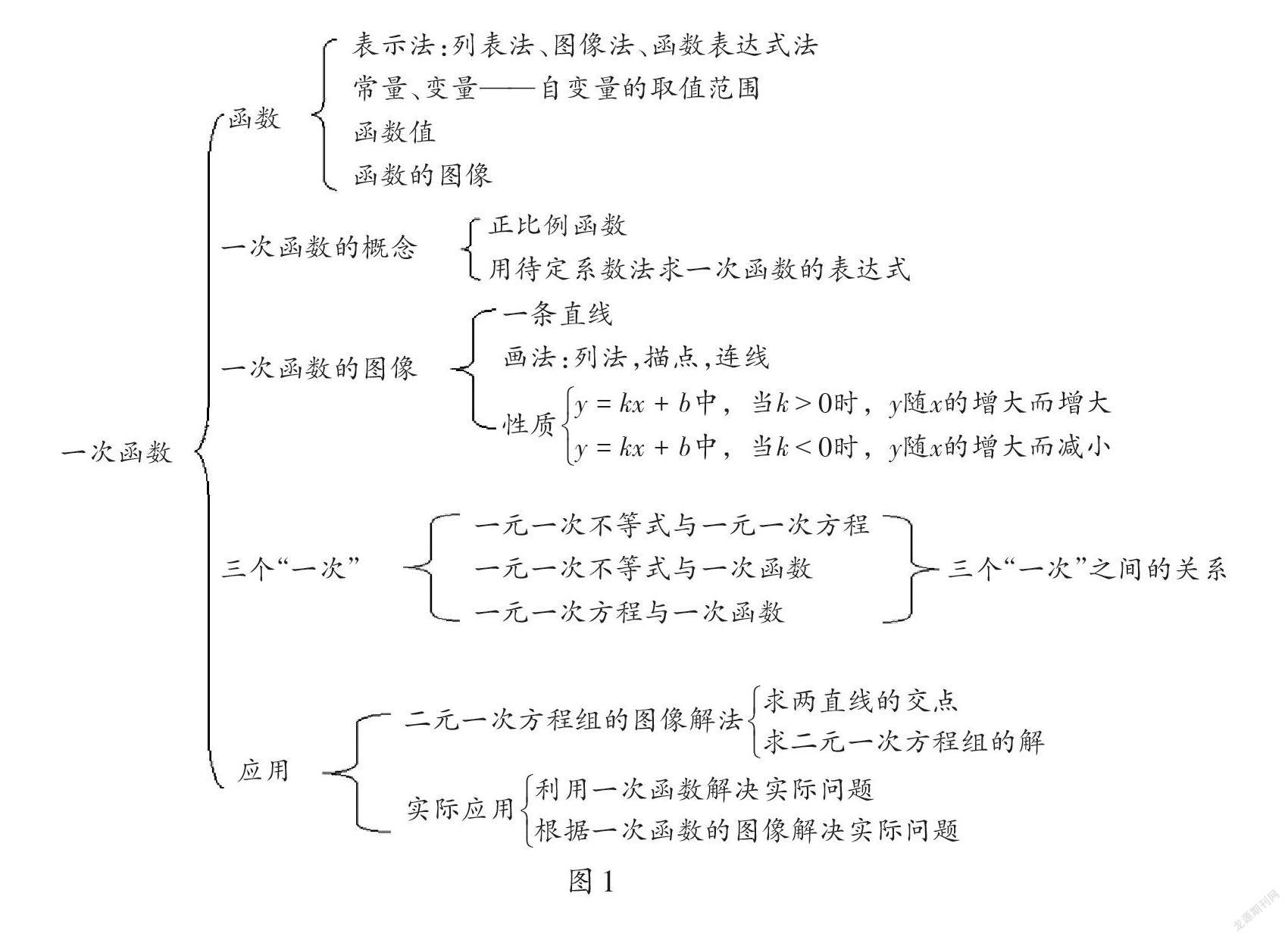
在今天的自习课上，老师让我们阅读教材并自学第六章 “一次函数”，要求我们尝试列出思维导图，了解本章有哪些知识点，自己发现了哪些问题，如何去解决这些问题。带着老师的要求，我仔细阅读了数学教材第136—167页，并进行了细致的梳理，感受到了与往常不一样的乐趣，也有了新的收获。

根据“一次函数”中的概念、图像及其性质和应用三大部分，我整理出了关于这章知识点的思维导图（如图1）。整理出这个图后，我能较以前更为清楚地知道一次函数相关知识的构成和知识之间的联系。

通过对教材的阅读和理解，我发现，一次函数的图像问题是一个新的知识。这是我第一次把一个数学式子和一个图像联系起来，类似于把我的名字和我的照片对应起来。我还发现，一次函数表达式中的k和b更加精确地决定了图像经过的象限和坐标轴的交点坐标;k值的正负性还决定了函数的增减性;直线与y轴的交点是（0，b）。我想这就是我们平时在数学学习中经常提到的“数形结合”思想。

我在梳理教材中的典型例题和练习时，发现大多数简单题型自己能解答，而一部分综合性、开放性题目却无从下手，这也透露出我的思维不灵活、应变能力弱等问题。在以前的数学学习中，我们跟着老师的脚步轻松地完成了学习，但当我们独立解决问题时，却发现一切都不那么简单，每一步的探究都很艰难。这就是“看似寻常最奇崛，成如容易却艰辛”。

我必须对每个环节、每种题型进行充分、细致的研究。通过研究，我总结出了图像的性质，借助图像的性质进一步得到一次函数的性质。因此，我明白了知识真正的形成往往来源于自主探究。只有放手探究，我们的潜力与智慧才会充分发挥，才会展现真实的自我。我也明白了学习目标都是围绕着我们的成长与发展而制定的，让我们真正地理解和掌握知识，而不是盲目地陷入“题海”。

在研究一次函数的应用时，我发现，其本质就是一次函数与行程应用题的结合，一次函数与一元一次方程的结合，不等式以及实际问题的结合。它也是刻画现实世界中数量关系的一种数学模型。当函数中一个变量的值确定时，可由相应的方程和不等式确定另一个变量的值或取值范围。这一部分的知识还渗透了转化的数学思想、数形结合思想、运动变化思想以及特殊与一般思想，让我意识到在利用一次函数及其图像解决实际问题的过程中，要充分发挥我们的数学应用能力。

通过这一次的自主学习，我明白了真正的知识不全是从教材和老师那里获得的，我们可以和老师共同探究协作，培养自学能力和探究能力，寻觅真知。

教师点评

该同学能够通过自主阅读教材、自学教材，尝试梳理知识，形成知识网络，了解知识的内在联系，感受其中的数学思想，养成自学和探究能力，不断提升自己的数学素养，值得同学們学习。

（指导教师：倪文娟）