纵横联系，数学更有趣

朱月红

数学世界浩瀚如海，数学知识千差万别，但不同知识之间却存在“亲缘”关系、相似之处。只有学会有联系地思考，我们才能获得更有益的知识。下面，我们以苏科版八年级上册第五章“平面直角坐标系”为例，共同体会其中的奥妙。

一、类比学习，形成完整的知识结构

数学的概念与概念之间具有联系性。当知识与知识联系在一起时，新知识因为有了“根”才“成活”，进而成为“活”的知识，最终转化为“力量”。

请同学们思考一下：“平面直角坐标系”的“上一代”是什么？研究了什么内容？怎么研究的？后续将研究什么问题？

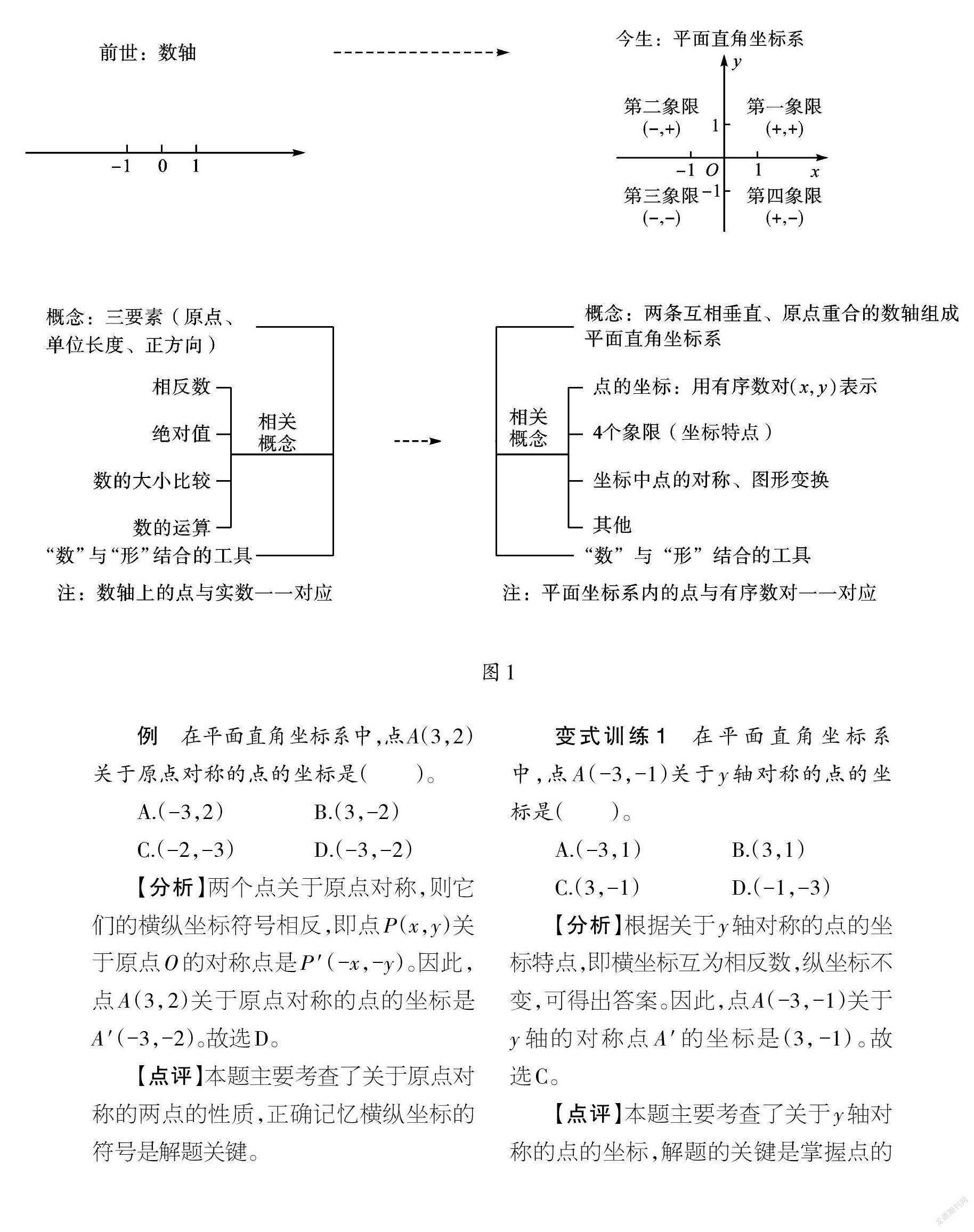
如果类比数轴（一维）研究的对象和路径，来研究两条数轴（二维），建立平面直角坐标系，对比“前世”（数轴）和“今生”（平面直角坐标系）（如图1），同学们是不是有种豁然开朗的感觉？

二、有逻辑地思考，让思维更灵活

有的同学每攻克一道难题，就志得意满，其实这还远远不够。同学们要学会从多个角度思考：这道题还有没有其他解法？如果遇到同类问题，自己还能快速地做出来吗？

例 在平面直角坐标系中，点A（3，2）关于原点对称的点的坐标是（ ）。

A.（-3，2）    B.（3，-2）

C.（-2，-3）  D.（-3，-2）

【分析】两个点关于原点对称，则它们的横纵坐标符号相反，即点P（x，y）关于原点O的对称点是P′（-x，-y）。因此，点A（3，2）关于原点对称的点的坐标是A′（-3，-2）。故选D。

【点评】本题主要考查了关于原点对称的两点的性质，正确记忆横纵坐标的符号是解题关键。

变式训练1 在平面直角坐标系中，点A（-3，-1）关于y轴对称的点的坐标是（ ）。

A.（-3，1） B.（3，1）

C.（3，-1）  D.（-1，-3）

【分析】根据关于y轴对称的点的坐标特点，即横坐标互为相反数，纵坐标不变，可得出答案。因此，点A（-3，-1）关于y轴的对称点A′的坐标是（3，-1）。故选C。

【点评】本题主要考查了关于y轴对称的点的坐标，解题的关键是掌握点的坐标特点。

变式训练2 若点P（x，y）在第三象限，则点M（y-1，-x+1）在第     象限。

【分析】首先，根据各象限内的点的横、纵坐标的特征，判断出x、y的正负情况;再根据对横、纵坐标的理解，判断出点M的横、纵坐标的正负情况;最后，根据各象限内的点的坐标特征进行解答。

方法一（特殊值法，解决填空、选择题最快捷的方法）：

令x=-1，y=-1，則y-1=-2，-x+1=2，

∴M（-2，2）。

故点M在第二象限。

方法二（根据各象限内的点的坐标特点）：

∵点P（x，y）在第三象限，

∴x<0，y<0，

∴y-1<0，-x+1>0。

故点M（y-1，-x+1）在第二象限。

方法三（数形结合，如图2）：

∵点P（x，y）在第三象限，

∴x<0，y<0，

∴-x>0，y<0，

∴点（y，-x）在第二象限，

∴点（y-1，-x+1）为点（y，-x）向左平移1个单位，向上平移1个单位，平移后的点仍在第二象限。

故点M（y-1，-x+1）在第二象限。

【点评】一道例题有多种变法，一个问题有多种解法，同学们只有做到触类旁通，才能真正弄懂、弄透一类题，才能以不变应万变，享受学习数学的乐趣。下面我们再变一变，请同学们试一试。

变式训练3 在平面直角坐标系中，若点P（a-3，1）与点Q（2，b+1）关于x轴对称，则a+b的值是（ ）。

A.1 B.2 C.3 D.4

变式训练4 在平面直角坐标系中，过不同的两点 P（2a，6）与 Q（4+b，3-b）的直线 PQ //x 轴，则 a，b满足的条件是             。

同学们要学会从不同角度、不同思想、不同方法和不同的运算过程进行联想，这样可以将一些繁琐的甚至枯燥无味的习题变得充满趣味。

[参考答案]

变式训练3.C;变式训练4.a≠[12]，

b=-3。

（作者单位：江苏省泰州市高港区教师发展中心）