不同结构体系独塔斜拉桥地震响应分析
吴凤民
(湖南省怀化市农村公路建设办公室, 湖南 怀化 418000)
0 引言
近年来,随着国内桥梁建设的飞速发展,跨河跨海大桥日益增多,桥梁跨径也逐渐增大。斜拉桥以其梁体尺寸小、跨越能力大、受桥下净空限制小等优势,成为了桥梁设计比选时的首选桥型之一。斜拉桥发展至今,已出现了多种结构体系,不同结构体系之间动力特性差异较大,对于地震响应也表现出不同的特点[1]。独塔斜拉桥最常见的体系为刚构体系与漂浮体系,为探究这2种体系下独塔斜拉桥的地震响应差异,本文以某独塔斜拉桥为研究对象,采用反应谱法进行了计算分析,相关研究结果可供独塔斜拉桥抗震设计时参考。
1 工程概况
湖南某斜拉桥主桥设计为独塔双索面预应力混凝土箱梁结构,全长359 m,其中主跨196 m、边跨为(101+62)m=163 m。斜拉索呈扇形布置,主塔两侧各设26对。斜拉索在主梁上的基本索距为7.5 m,边跨尾索区为5 m,塔上索距为2.5 m。主塔结构形式为钻石型,边跨设一个辅助墩。主梁为预应力混凝土结构,截面形式为单箱3室箱形截面。其总体布置见图1。
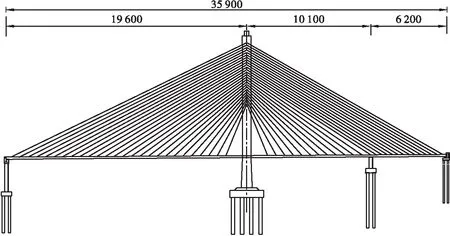
图1 独塔斜拉桥立面布置(单位: cm)
该桥主塔由塔柱与下横梁组成,总高130.586 m,采用C50混凝土。主梁横断面全宽为29.5 m,主梁梁高3 m,采用C55混凝土,主梁横断面见图2。
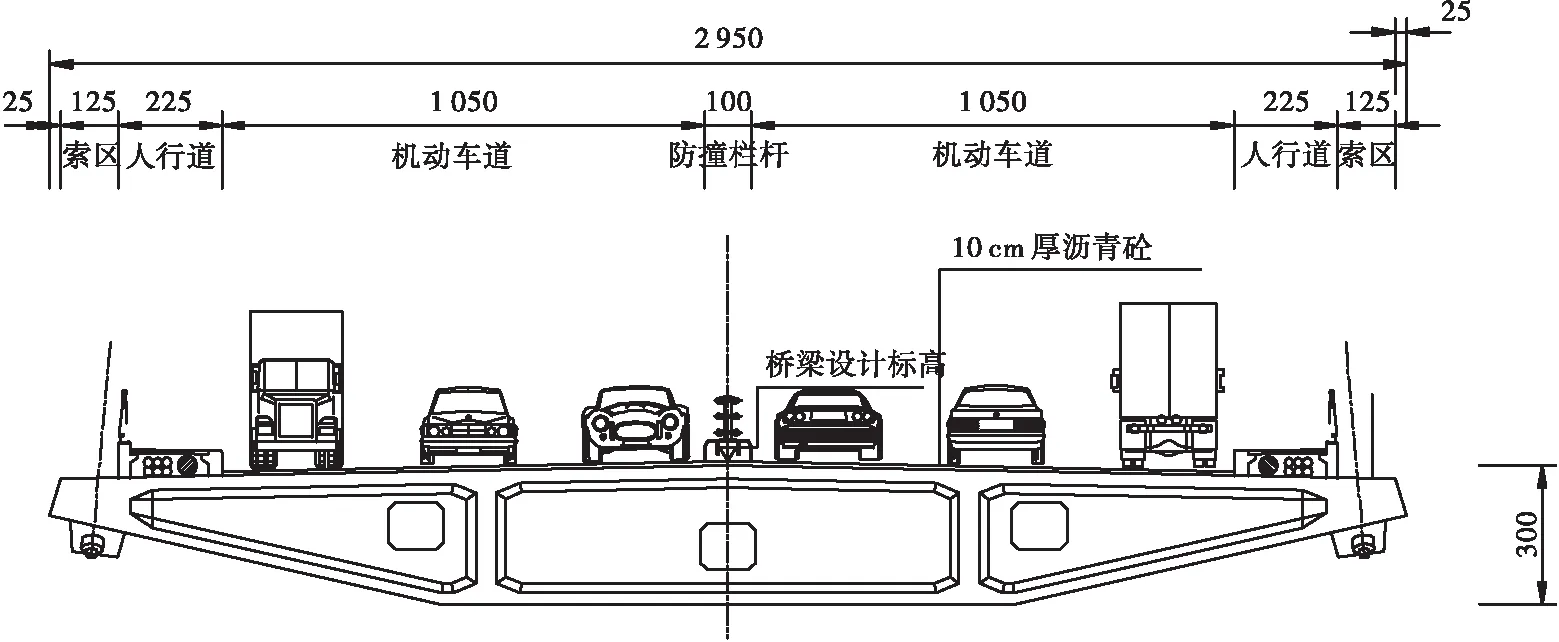
图2 主梁横断面(单位: cm)
2 有限元模型的建立
使用Midas/Civil建立该桥刚构体系(模型A)与漂浮体系(模型B)有限元模型,全桥采用空间梁单元建模,模型共402个节点、295个单元。主梁采用脊梁模式建立,与斜拉索之间采用刚性连接;主塔单元尽可能细分以避免影响其堆聚质量的分布、振型的形状和地震力的分布;拉索采用桁架单元,不考虑垂度效应;主塔塔底采用固结约束,辅助墩与桥台采用一般连接,约束Dy、Dz。由于刚构体系与其主要差别为主塔与主梁的连接方式,漂浮体系主梁纵向未进行约束,刚构体系则为塔墩梁固结,因此,此处仅示出漂浮体系(模型B)有限元模型(见图3)。
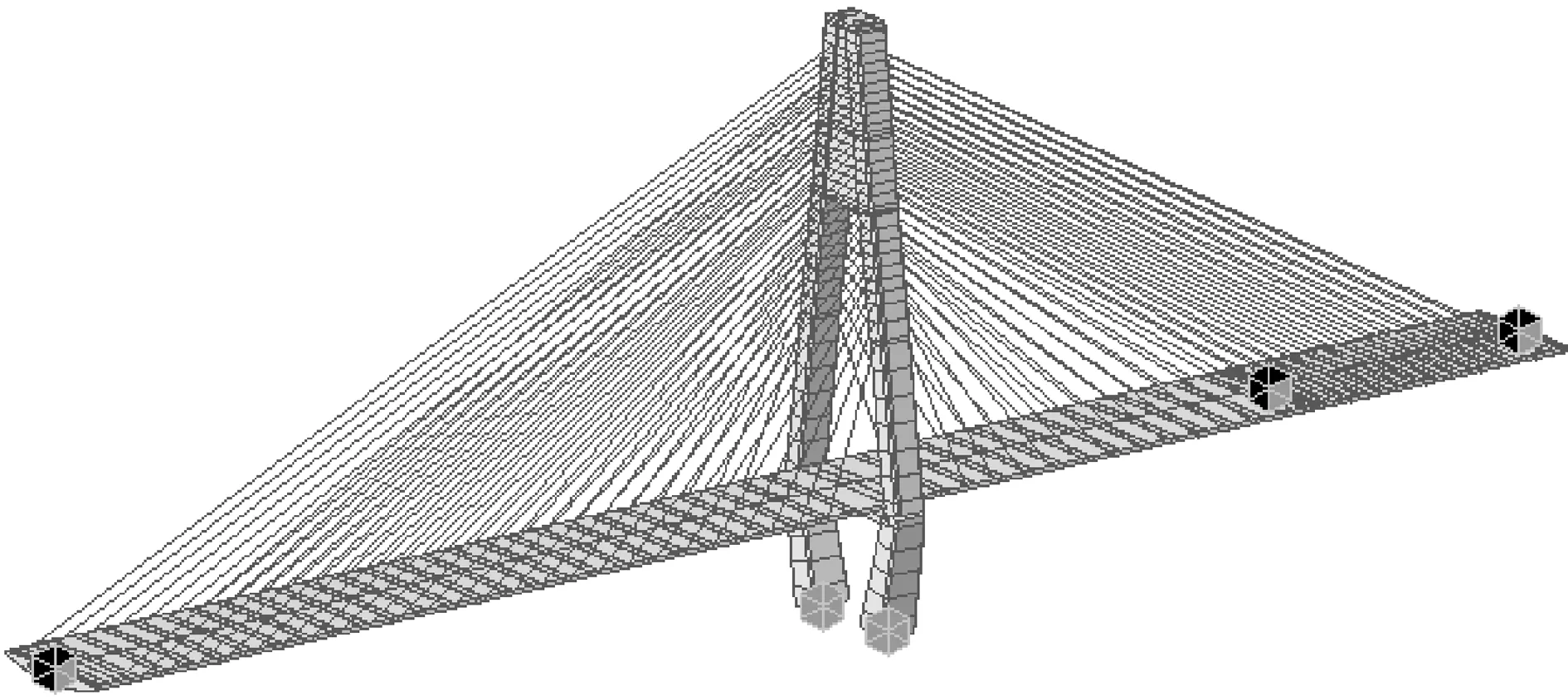
图3 独塔斜拉桥漂浮体系有限元模型示意
3 反应谱法参数选取
根据《公路桥梁抗震设计细则》(JTC/T B02-01—2008)中5.2.1与5.2.4要求,结合设计文件与桥址处的地理环境,确定该桥抗震设防烈度为7度,结构阻尼比为0.02,阻尼调整系数Cd为1.32,水平向设计加速度反应谱中特征周期Tg为0.35 s,场地类型为Ⅱ类,场地系数Cs为1.0,抗震重要性系数取1.7。
综上所述,该桥水平向设计加速度反应谱中的各种系数取值见表1。

表1 水平设计加速度反应谱系数取值表TgCiCsCdA0.351.71.01.320.05 g
由表1可求得Smax=0.252 45 g。水平设计加速度反应谱见图4。

图4 水平设计加速度反应谱
根据《公路桥梁抗震设计细则》(JTC/T B02-01—2008)与该桥的设计文件可知,本桥桩基处于基岩上,因此竖向/水平向谱比函数R取0.65,竖向设计加速度反应谱见图5。
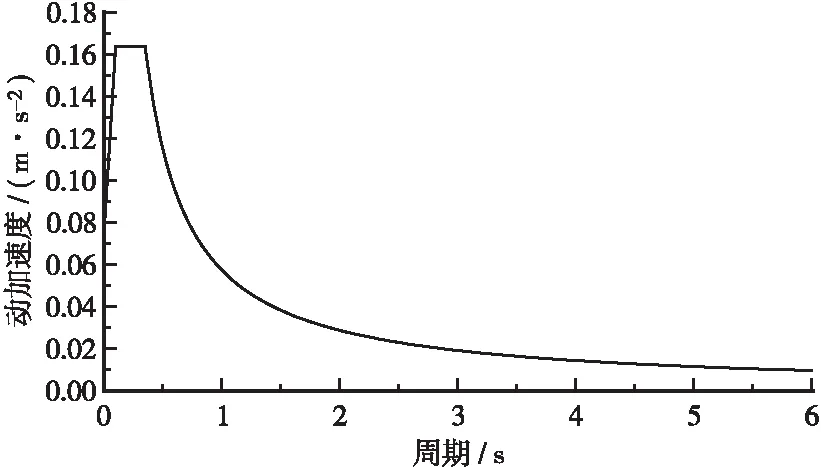
图5 竖向设计加速度反应谱
对于结构振型的二次组合,相较于SRSS法,CQC法可考虑振型之间的相互影响[2],因此,该桥结构的各阶振型采用CQC法进行组合。该桥主跨196 m,根据抗震规范的规定,在计算地震作用时除了考虑横桥向与纵桥向地震作用以外,还需考虑竖向地震作用[3-6],因此,该桥计算以下2种工况,并采用SRSS法对地震作用方向进行组合:① 工况1:纵桥向+竖桥向;② 工况2:横桥向+竖桥向。
4 反应谱法计算结果
对于独塔斜拉桥,其主梁地震响应峰值一般产生于跨中或端部位置;主塔地震响应峰值一般产生于塔顶、塔底或塔梁连接处[7],因此选取该独塔斜拉桥关键截面,具体位置如图6、图7所示。
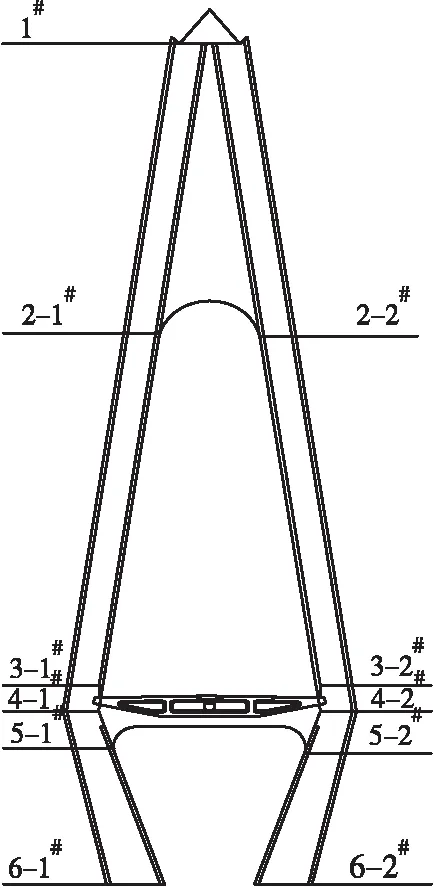
图6 主塔关键截面位置示意
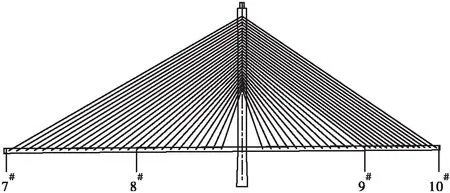
图7 主梁关键截面位置示意
4.1 位移计算结果
在纵向+竖向地震动组合作用下,两模型主塔下部3-1#截面至6-2#截面位移较小,最大值为模型B的纵向位移9.57 mm。模型B主塔中上部与主梁各关键截面均有较大位移,最大值为156.37 mm,最小值为86.92 mm。模型A对应截面位移明显较小,最大值为28.02 mm,最小值为15.30 mm。考虑因该桥主塔上部发生纵向位移后,漂浮体系塔梁之间未进行约束,导致主梁发生纵向摆动,并反作用于主塔;而刚构体系塔梁固结,使得主梁难以自由摆动,由于主梁位移受限制使得主塔的位移也有所限制,所以,模型B的主塔中上部与主梁各关键截面纵向位移明显大于模型A。在横向+竖向地震动组合作用下,两模型主塔下部以及主梁除中跨跨中位置外的各向位移均较小,最大值为模型B横向位移11.70 mm。而模型B主塔中上部与主梁跨中截面处横向位移略大于模型A,模型B最大值为主塔中横梁横向位移45.58 mm,最小值为主梁横向位移38.06 mm,模型A相应截面最大值为36.01 mm,最小值为18.94 mm。
图8、图9为工况1与工况2纵向位移对比图。模型A与模型B在地震作用下,由于组合了竖向震动,该桥的主梁跨中截面均产生了较大的竖向位移,模型B最大值为58.02 mm,模型A最大值为39.84 mm,所以,在抗震设计时应该重视主梁中跨跨中截面的受力破坏。
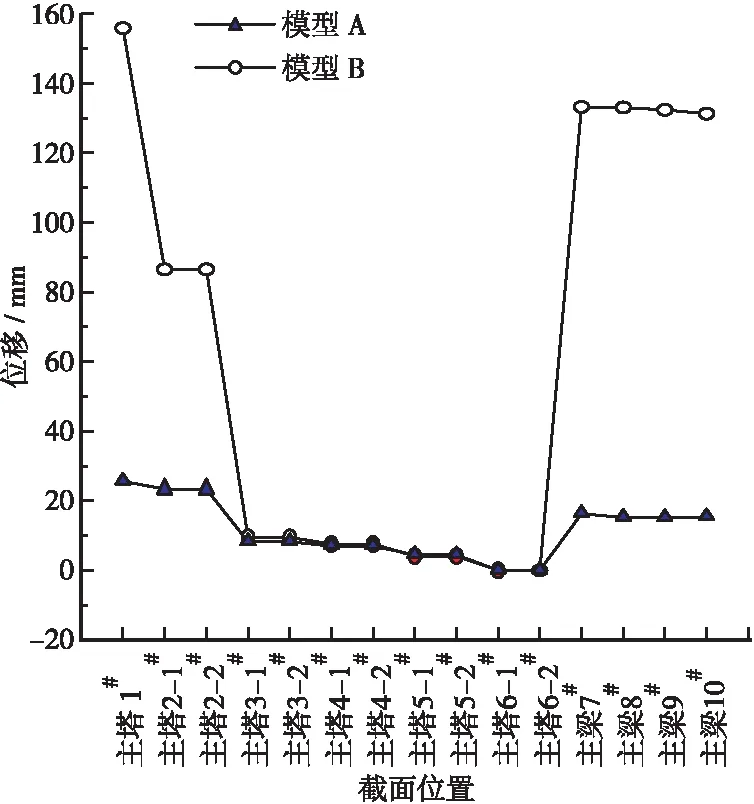
图8 工况1纵向位移对比图

图9 工况2横向位移对比图
通过2种工况的对比可发现,采用刚构体系可以更好地约束结构三向位移,该桥设计时也应特别注意主塔中上部截面纵向抗劈裂能力与横向抗弯能力。
4.2 内力分析
模型A与模型B在纵向+竖向地震动组合作用下,除轴力外,模型A与模型B主塔弯矩、剪力均显著大于主梁,且内力峰值均位于主塔底部,模型A 主塔底部轴力为9 538.24 kN,纵桥向弯矩为278 833.48 kN,纵桥向剪力为12 312.31 kN;模型B主塔底部轴力为9 223.57 kN,纵桥向弯矩为226 180.82 kN,纵桥向剪力为4 507.16 kN,说明主要受力部位为主塔,设计时应注意增强主塔底部截面的抗力。图10~图15为工况1与工况2的轴力、剪力、弯矩对比图。

图10 工况1轴力Fx对比图
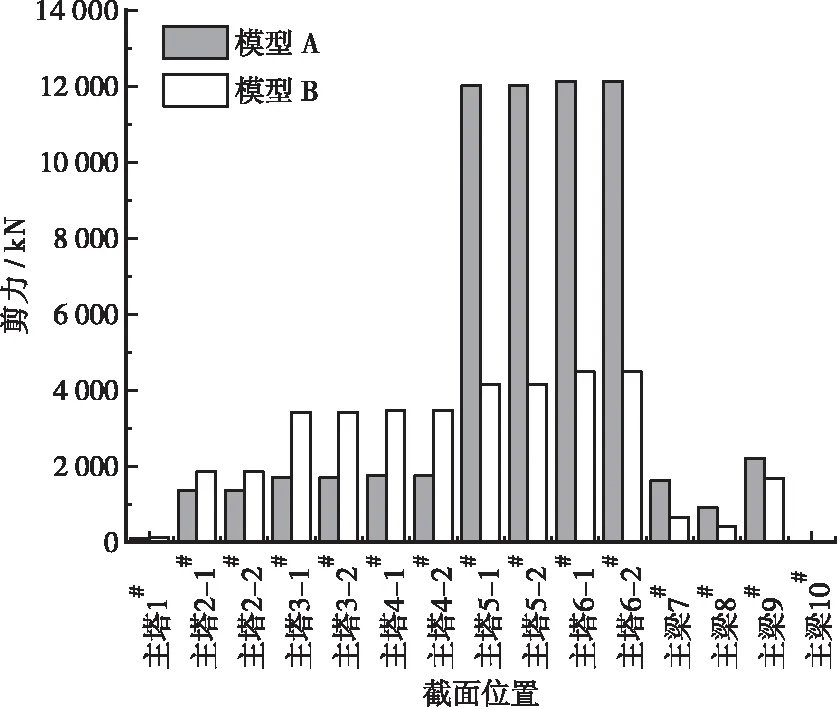
图11 工况1剪力Qz对比图
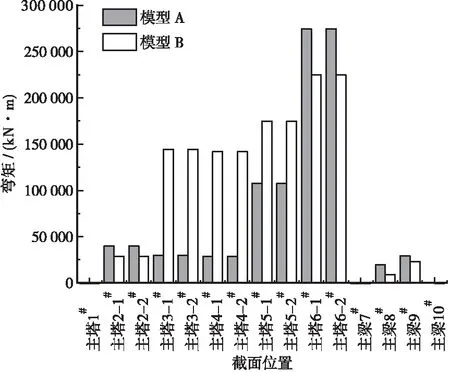
图12 工况1弯矩My对比图
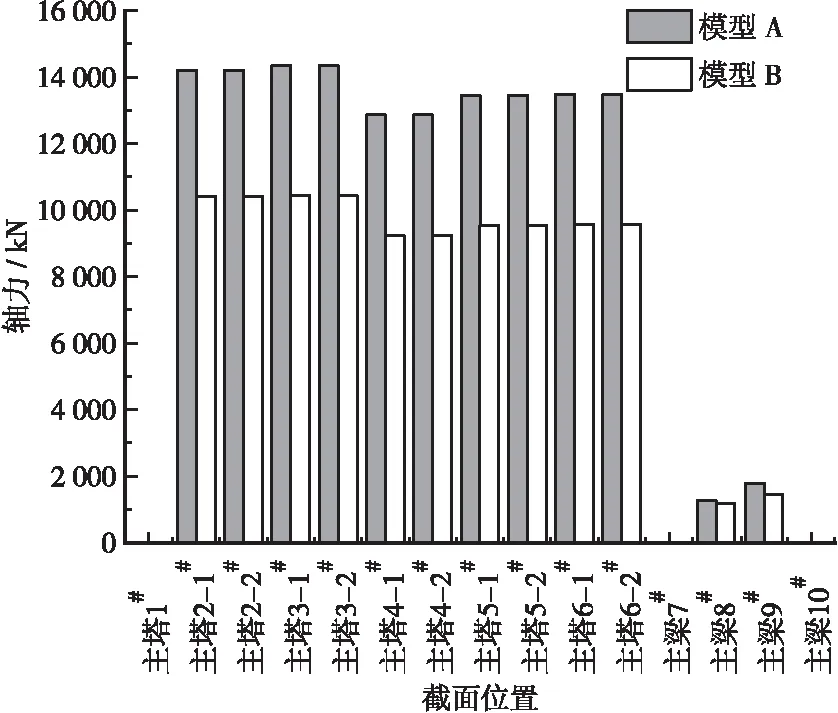
图13 工况2轴力Fx对比图
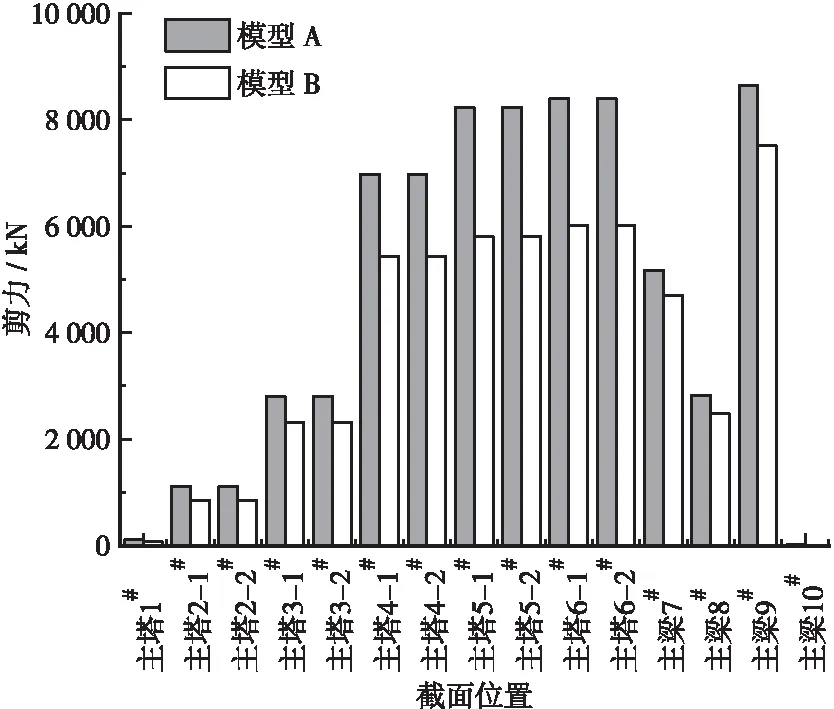
图14 工况2剪力Qy对比图
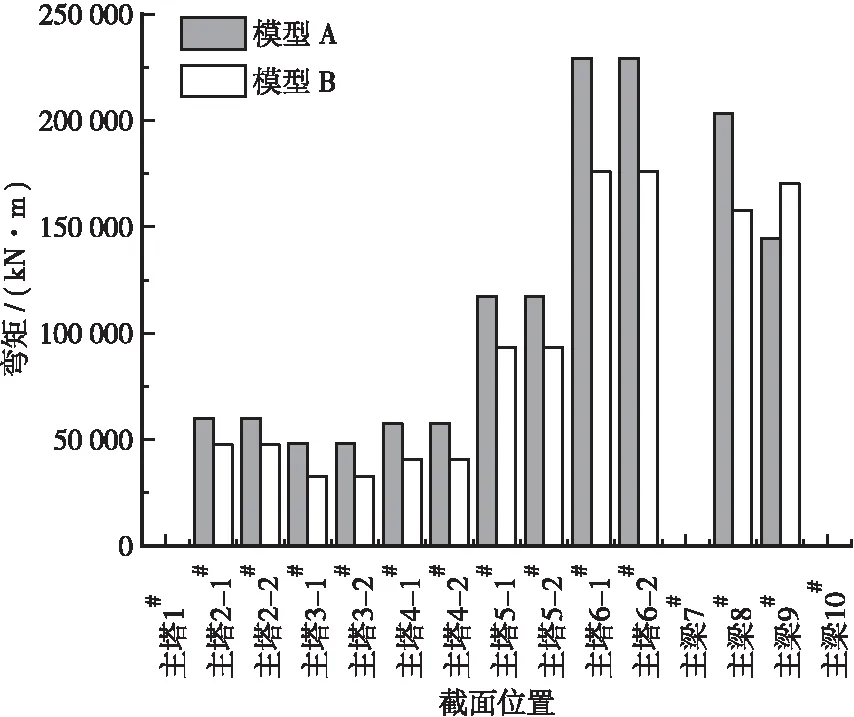
图15 工况2弯矩Mz对比图
在横向+竖向地震动组合作用下,模型A与模型B横桥向内力明显大于工况1,而纵桥向内力明显小于工况1,说明纵向或横向的内力主要由该方向的地震作用引起,纵、横向之间的内力耦合程度小。两模型内力峰值处于主塔底部与主梁中跨跨中位置,模型A横桥向轴力为16 327.70 kN,横桥向弯矩为229 416.51 kN·m,横桥向剪力为8431.61 kN。模型B横桥向轴力为13 066.95 kN,横桥向弯矩为176 146.78 kN·m,横桥向剪力为6035.51 kN,设计时也应注意增强主梁中跨跨中位置截面的抗力。由于纵桥向地震作用对该桥纵桥向内力效应影响明显大于横桥向,横桥向地震作用对该桥横桥向内力效应影响明显大于纵桥向,故工况1仅示出纵桥向内力结果,工况2仅示出横桥向内力结果。
5 结论
以某独塔斜拉桥为例,基于反应谱法,通过横向+竖向与纵向+竖向两种地震动组合对比分析了该桥2种不同结构体系的地震响应,计算结果表明:
1) 若采用漂浮体系,由于主塔中上部截面纵向位移与横向位移较大,设计时应特别注意纵向抗劈裂能力与横向抗弯能力,而采用刚构体系可以更好地约束结构三向位移。但不论采用何种体系,由于竖向地震作用的影响,设计时均不可忽略主梁中跨跨中截面的剪切破坏。
2) 由内力对比可知,该桥在地震作用下主要受力部位为主塔与主梁中跨跨中截面,且内力峰值均出现在主塔底部,因此,设计时应注意增强主塔底部与主梁中跨跨中截面的抗力。该桥横桥向内力响应普遍大于纵桥向,应注意加强整体的横向刚度。
3) 该桥采用刚构体系位移明显小于漂浮体系,整体内力稍大于漂浮体系,经综合对比可得,对于抗震设计,该桥更适于采用刚构体系。

