基于RBF神经网络的随机结构动力可靠度分析
唐翠兰, 帅一师, 雷顺成, 姚方舟
(1.湖南省交通科学研究院有限公司, 湖南 长沙 410015; 2.邵阳市交通建设质量安全监督站, 湖南 邵阳 420001)
0 引言
随着我国交通运输行业的飞速发展,大跨度桥梁结构日益增多。影响结构安全最关键的荷载,如地震荷载、强风荷载和车辆荷载等往往具有较明显的随机性,给设计者带来了较大挑战。大跨度结构在随机荷载作用下的响应及动力可靠度研究具有重要意义,近年来取得了丰富的研究成果。梅建松等[1]采用概率密度演化方法,分析了杆系拱桥在非平稳随机激励作用下的响应及可靠度;武芳文等[2]对苏通大桥进行了随机地震响应分析,并基于JC法和首次超越原则,分析了主梁关键截面的动力可靠度;鲁乃唯等[3]通过建立随机车流模型,研究了密集车流占有率对桥梁可靠度的影响规律。在已有动力可靠度的研究中,往往仅考虑载荷的随机性而忽视了结构参数的随机性。在实际工程结构中,参数的随机性是一直存在的,对计算动力可靠度有较大影响。因此,研究双重随机性的动力可靠度更具有实用价值。
目前结构动力可靠度分析仍以随机有限元方法模拟为基础,考虑结构参数随机性后,随机变量的数量大大增加。对于大跨度桥梁等复杂结构而言,传统的Monte Calo法计算代价太大,基本上不可能完成。随着响应面法和神经网络的蓬勃兴起,动力可靠度分析有了新思路[4],即以有限次的有限元计算结果为训练样本,拟合出复杂的功能函数,然后基于功能函数便可通过传统可靠度分析方法得出结果,从而使计算效率大大提高。
本文以某大跨度刚构桥为工程背景,引入了RBF神经网络法对功能函数进行拟合,通过MALTAB编写了基于RBF神经网络法的主程序并调用ANSYS程序接口,实现了结构响应有限元计算与动力可靠度分析的自动求解。通过算例表明了该方法的高效性。
1 动力可靠度功能函数的建立
随机结构静力可靠度分析中的功能函数一般表示为[5]:
Z=R-D
(1)
式中,R为结构的某种界限值(如抗力值);D为结构的静力响应值。
当考虑结构双重随机性时,其响应过程亦具有随机性。于是,结构动力可靠度的功能函数可参考静力可靠度功能函数的推导方法构建[6],即:
Z(t)=R-D(t)
(2)
由式(2)可知,动力可靠度功能函数是时间的函数,即功能随机过程[7]。由于较静力可靠度功能函数多了时间的维度,无法直接对其进行求解。
现将式(2)在时间区段[0,T]内进行极小值变化,从而有:
Z(t)min=R-d(t)maxt∈[0,T]
(3)
式中: d(t)max为结构响应D(t)在时间区段[0,T]内的最大值;Z(t)min为时间区段[0,T]内的可靠度最小值; 可将此作为结构在时间区段[0,T]内的动力靠度。
目前求解d(t)max的方法多基于首次超越破坏准则[8]。我国抗震规范[9]给出了d(t)max的计算方法,即:
d(t)max=ησd
(4)
式中,η为无量纲的随机变量。
其方差和均值分别为:
(5)
(6)
σd为结构随机响应的均方值,对于线性单自由度系统,则有:
(7)
式中:S(ω)为随机荷载功率谱密度函数;H(ω)为系统频率反应函数,是系统刚度k、m以及阻尼比ζ的函数。对于随机结构,由于结构参数k、m、ζ具有随机性,H(ω)也是随机函数,故在特定的随机荷载激励下,σd是结构参数k、m、ζ的函数,也是随机分布的,在多自由度系统亦是如此。
将式(4)代入式(3)中,得到随机结构的动力可靠度功能函数为:
Z=R-ησd
(8)
若考虑结构的恒载G和活载Q时,式(8)变成:
Z=R-G-Q-ησd
(9)
于是,通过以上方法,结构动力可靠度问题便转化为静力可靠度问题[7]。
假设X=(x1,x2,…,xn)为结构参数的随机变量(如弹性模量、容重、阻尼比等),式(9)可表示为:
Z=R-G(X)-Q(X)-ησd(X)
(10)
由于式(10)为含多变量的隐函数,采用传统的一次二阶矩无法直接进行求解。当功能函数为隐函数时,通常可采用以下两种方法求解其可靠度: ① 采用Monte Calo抽样法生成结构参数序列,代入有限元中计算得到结构的响应值,由此计算结构可靠度;②采用响应面法拟合得到近似的显函数,然后采用JC法计算结构可靠度。前者需要巨大的抽样样本,有限元计算量太大,不适合实际工程结构;后者拟合能力有限,速度和精度不足。本文选取径向基神经网络(RBF)进行隐式功能函数的拟合。
2 基于RBF神经网络法的动力可靠度分析
与常规的响应面法不同,RBF神经网络根据样本学习和训练得到的net是映射关系,而非具体的显性函数表达式,若后续采用JC法求解可靠度指标则必须求解映射关系net的一阶偏导数,这一过程比较复杂而且容易出错。为了避开这一难题,本文采取MATLAB优化工具箱的线性规划算法替代JC法来求解结构可靠度,下面对其进行简单介绍。
假定是x1,x2,…,xn是n个服从高斯分布独立随机变量,在标准正态坐标系中,可靠度指标为坐标原点到极限状态曲面的最短距离[5]。基于这一思路可将JC法中搜寻验算点的问题转化为最优问题[7],即:
s.t.gX(x)=gX(x1,x2,…,xn)
(12)
选取RBF神经网络训练样本时采用均匀试验设计法[10-11],该方法能确保设计点在设计空间内均匀分布,每个参数和每个水平只需做1次试验,合适的数量却不失代表性,从而提高训练效率。
本文采用MALAB编制分析主程序,ANSYS作为有限元计算分析手段,具体分析步骤如下:
1) 以结构随机变量的均值为初值建立ANSYS参数化模型,计算得到响应的各阶矩,按式(5)和式(6)计算得到η的方差和均值;
2) 确定结构随机参数变量。对于桥梁结构,可选用对静动力响应值以及结构抗力值影响较大的参数作为随机变量,如结构的弹性模量、容重、阻尼比和材料强度等参数。
3) 确定训练样本输入向量。根据均匀试验设计法生成样本点,通过MATLAB生成的每组随机变量样本点建立ANSYS有限元模型并进行分析,计算结构响应σd并将结果写入文件供MATLAB读取[7]。
4) 以样本点和响应结果σd作为RBF神经网络输入和期望输出,采用自动寻优的方法进行RBF神经网络训练:从一个隐藏层节点开始训练,对神经网络的模拟误差进行检验,当误差精度不满足要求时,让神经网络自动对隐藏层神经元进行数量的增加;而根据每次循环生成的最小误差对应的输入向量,会生成新的一个隐藏层节点,然后重新检查新一循环的神经网络误差,并对该过程进行重复,直至满足精度要求或达到神经元数上限。
5) 根据训练好的RBF神经网络,利用MATLAB线性规划最优算法求解可靠度指标β,则结构可靠度为Pr=Φ(β)。
3 算例分析
3.1 工程背景
以某大跨度斜拉桥为工程背景,该桥梁为双塔双索面半漂浮体系斜拉桥,其桥跨布置为(181.9+450+181.9)m,主桥全长为813.8 m。索塔处主梁以横向抗风支座及竖向支座为边界,并在各塔梁支座纵向处设置2个粘滞性阻尼器;过渡墩处通过墩顶竖向支座对主梁进行约束。主桥斜拉桥桥型立面布置见图1。斜拉桥主梁为流线型扁平钢箱梁(正交异性桥面板),如图2所示;主梁中心线处截面梁高为3 m,全桥梁宽均为30.5 m,主梁采用Q345D钢材,共分为17个吊装节段。采用高强预应力钢绞线(抗拉强度为1 860 MPa)作为斜拉索,斜拉索标准索距为12 m,加密区索距为5 m。
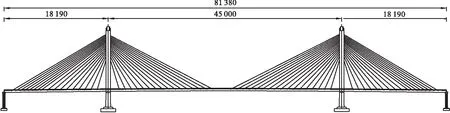
图1 斜拉桥桥型布置(单位: cm)
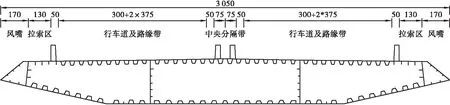
图2 斜拉桥横断面布置(单位:cm)
利用通用有限元程序建立斜拉桥有限元模型。主梁建模方式采用单主梁鱼骨刺模式,主梁单元为BEAM4单元,刚臂采用MPC184刚性梁单元模拟。索塔为BEAM188单元,斜拉索则采用LINK10仅受拉杆单元进行模拟。为考虑斜拉索结构的垂度效应,在计算分析模型中引入Enrst通用公式来修正斜拉索的弹性模量。斜拉桥有限元模型见图3。
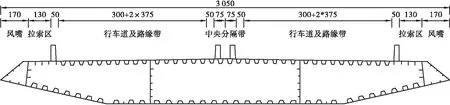
图3 有限元模型图
3.2 随机地震动响应分析
为了快速有效得到斜拉桥随机地震响应,本文采取直接求解运动方程的虚拟激励法[12]。即通过在结构有限元模型中各支点处施加大质量块(本文采用mass21质量单元施加,质量为结构整体质量的106倍),使得支点处质量矩阵几乎占据结构总质量矩阵的全部贡献,从而保证支点处的响应加速度等于输入的地震加速度,该方法可大大简化虚拟激励荷载的构造和输入工作[13]。
对于大跨度斜拉桥结构,其自振周期长、低频成分多,可采用杜修力模型作为地震加速度功率谱输入模型,从而克服柔性结构低频振动能量过大造成奇异点的缺陷问题。杜修力模型表达式为:
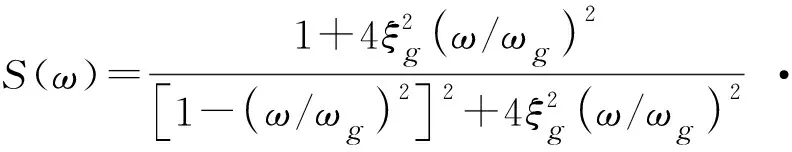
(13)
式中:S0表示白谱强度;ωg表示场地土层阻尼比;ξg表示场地土层卓越频率;D表示加速度脉冲宽度。
该桥所在地区地震基本烈度为Ⅶ度,地震峰值加速度为0.05 g,反应谱特征周期为0.35 s。根据文献[14]可以确定杜修力模型参数如下:S0=17.26 cm2/s3,D=0.011 4,ω0=1.83,ωg=13.03,ωg=0.97,Tg=13.66。进行三维地震联合输入时,X、Y、Z等3个方向的加速度输入比值为1∶0.85∶0.65。图4为随机地震激励加速度功率谱输入曲线[2]。
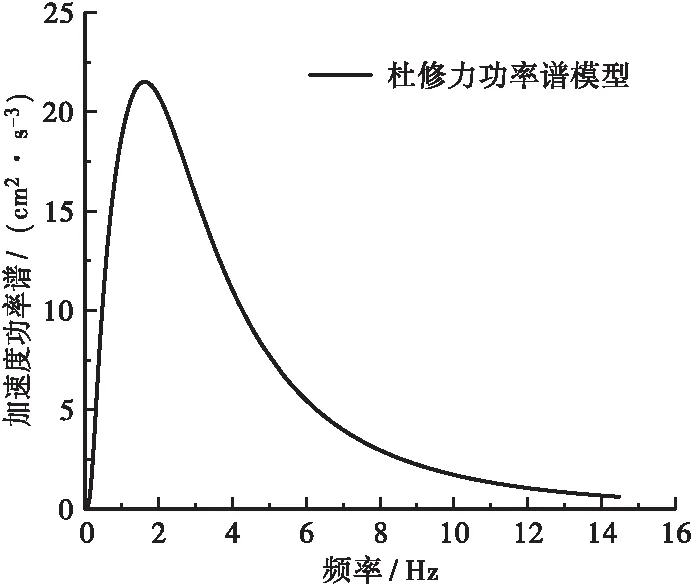
图4 随机地震加速度功率谱曲线
本文在计算随机地震动响应时,采用多维多点随机地震输入方式[13]。进行主塔动力可靠度分析时,考虑了大桥在地震激励、恒载和活载作用下3种荷载工况。当结构参数取其均值时,各工况下主塔响应如图5~图7所示。
根据图5~图7可知,主塔纵向弯矩响应随塔高增大而减小,本文选取塔底、下横梁处及上横梁处索塔截面为主塔动力可靠度分析的目标截面。
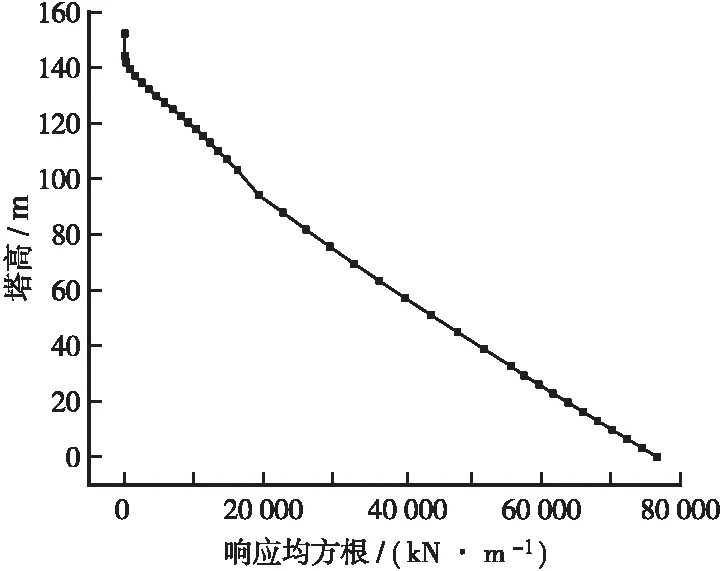
图5 随机地震作用下主塔弯矩响应均方根
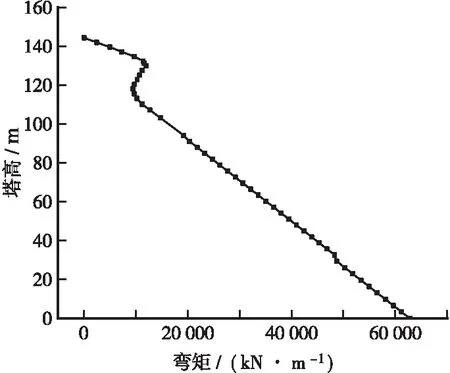
图6 恒载作用下主塔弯矩
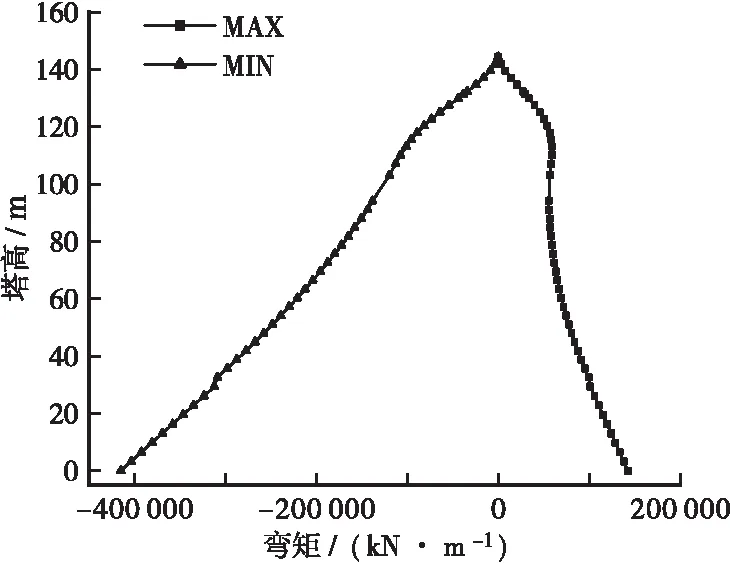
图7 活载作用下主塔弯矩包络图
3.3 主塔动力可靠度分析
选取主塔混凝土弹性模量、容重、抗压强度和阻尼比作为结构随机参数[6],其统计特性见表1。根据第3节所述分析步骤,对主塔关键截面承载力进行考虑双重随机性的动力可靠度分析。RBF神经网络训练过程表现出较快的拟合速度,本试验经过10次训练后便达到了设定的目标精度,见图8。主塔关键截面动力可靠度计算结果见表2。
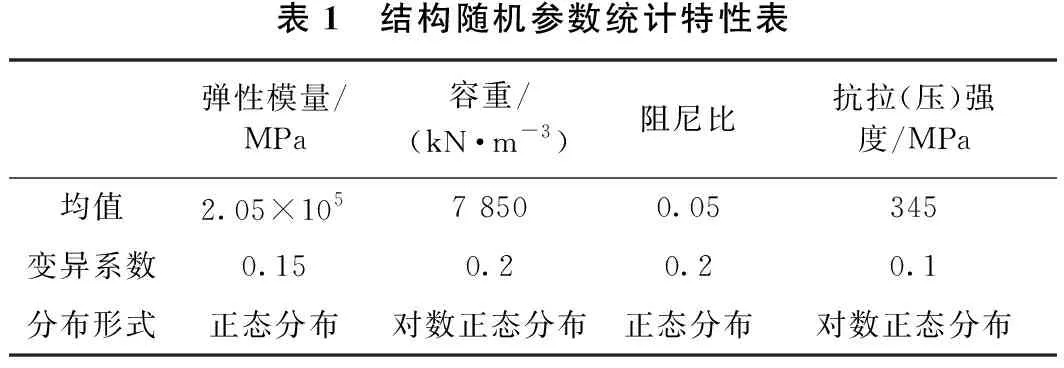
表1 结构随机参数统计特性表弹性模量/MPa容重/(kN·m-3)阻尼比抗拉(压)强度/MPa均值2.05×1057 8500.05345变异系数0.150.20.20.1分布形式正态分布对数正态分布正态分布对数正态分布
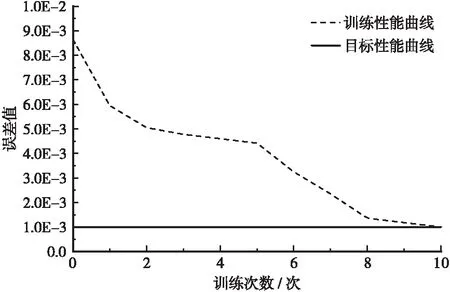
图8 训练误差图

表2 主塔截面动力可靠度计算结果截面RBF神经网络BP神经网络响应面法训练次数/次有限元计算次数/次可靠度值迭代次数/次有限元计算次数/次可靠度值误差/%塔底10254.926665.011.80下横梁处索塔12254.769994.662.15上横梁处索塔10255.227775.474.57
表2给出了采用RBF神经网络算法和BP神经网络响应面算法计算得到的主塔关键截面承载能力动力可靠度。结果表明,RBF神经网络法与BP神经网络响应面法计算结果的差值均在5%以内,但前者所需的有限元计算次数远少于后者,说明RBF神经网络法在保证精度的同时,具有更快的拟合速度,对于实际工程复杂结构进行动力可靠度分析是可行的。同时,主塔关键截面承载能力动力可靠度均大于4,说明该桥主塔有较好的抗震性能和强度储备。
4 结论
本文在结构静力可靠度功能函数建立方式的基础上进行了拓展,推导出了在随机地震作用下结构动力可靠度分析的功能函数。通过MATLAB生成随机参数序列并进行随机地震响应有限元求解。以响应结果作为训练样本,引入RBF神经网络法对功能函数进行拟合。最后采用线性规划的方法替代传统JC法求解可靠度指标,避开了求解神经网络一阶偏导这一难题。计算结果表明:RBF神经网络只需较少的训练样本便能达到BP神经网络同样的计算精度,说明RBF神经网络具有更快的拟合速度,对复杂工程结构引入动力可靠度分析具有重要意义。

