带金属阻尼器的框架结构抗震性能分析
黎浩宇, 左 啸, 陈 峥
(湖南省交通水利建设集团有限公司, 湖南 长沙 410008 )
0 引言
近百年来,我国经历了多场大型地震,最著名的有1976年河北唐山7.8级地震、2008年四川汶川8级地震和2010年青海玉树地震,这些地震给我国带来了惨重的生命和财产损失。研究显示,在地震作用下倒塌的建筑中,塑性铰数量主要出现在柱端,因其不能有效地消耗地震产生的能量,造成变形过于集中[1]。而要消除“梁铰”破坏,仅仅按照规范进行“强柱弱梁”设计是远远不够的。
为了提高框架结构的延性,可在框架结构中附加金属阻尼器。金属阻尼器是一种位移型的阻尼器,具有较好的滞回性能[2]。若应用于框架中,在地震作用下,金属阻尼器是整个结构的“排头兵”,可以通过耗散地震能量,保护主体不受损伤。本文利用OpenSees有限元软件,建立附加金属阻尼器的框架结构分析模型。主要分析了附加金属阻尼器框架结构在往复荷载作用下的抗震性能,并开展了阻尼器不同布置位置、弹性模量的参数分析,研究成果可为金属阻尼器的设计与应用提供参考。
1 结构概况
1.1 框架结构
某平面二维框架结构如图1所示,该框架结构为二维两层两开间钢筋混凝土结构,其总高度为7.2 m。该场地设计基本风压0.35 kN/m2,地面粗糙类别为B类。框架恒荷载为1.5 kN/m2,活荷载为2.0 kN/m2,根据规范[3-4]和软件YJK对此框架进行配筋设计,具体梁、柱尺寸以及配筋图如图2所示。其中梁柱混凝土强度等级为C30,纵筋均为HRB335。混凝土和钢筋的物理参数分别见表1和表2。
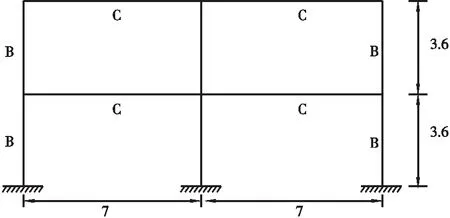
图1 某平面二维框架结构(单位: m)
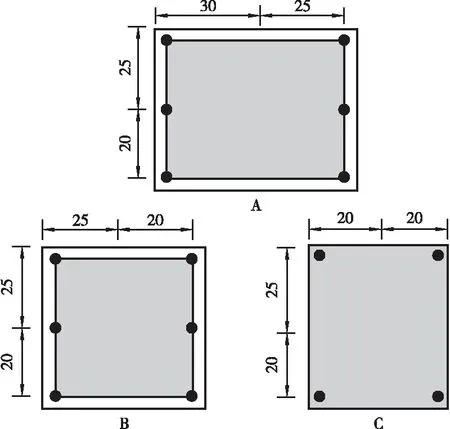
图2 梁、柱配筋图(单位: cm)

表1 混凝土物理参数构件材料弹性模量Ec/MPa坍落度/mmFcu/MPa泊松比vC30混凝土3.25×1049034.480.195

表2 钢筋物理参数钢筋类别弹性模量Es/MPa屈服强度/MPa直径/mm箍筋(HRB335)2.0×105248.214
2 OpenSees简化模型建立及加载
2.1 框架的模拟
框架的模拟主要包含单元和本构材料的选择以及边界条件的模拟。本文所设计的框架结构只考虑梁和柱,对梁柱单元的模拟均采用分布塑性铰纤维单元(Force Beam Column Element),梁的长度和柱的高度依据框架结构尺寸设置,对梁柱节点不进行特殊处理,直接进行固接,柱的边界条件为底部固结。
在OpenSees有限元数值仿真中,梁柱纤维截面采用“fiberSection”进行定义,截面纤维主要包括混凝土纤维和钢筋纤维,本文分别选用Concrete02混凝土材料本构和Steel02钢筋材料本构,同时考虑箍筋的约束作用[5]。
2.2 金属阻尼器的模拟
国内外学者[6]开展了大量的金属阻尼器拟静力试验研究,结果表明金属阻尼器的滞回特性可看作随动强化的双折线滞回关系,并且在往复位移作用下会出现等向强化特性,这与OpenSees中Steel01钢材本构的滞回特性相符合。Steel01钢材本构为双折线本构,应力-应变本构骨架曲线如图3所示。本文采用OpenSees中twoNodeLink单元配合Steel01钢材本构模拟金属阻尼器。

图3 Steel01钢材应力-应变骨架曲线
在OpenSees中Steel01钢材本构的模型代码为:uniaxialMaterial (‘Steel01’, $matTag, Fy, E0, b, a1, a2, a3, a4)。其中,matTag表示材料编号;Fy表示抗压强度;E0表示弹性模量。
2.3 附加金属阻尼器的框架结构有限元模型
前文介绍了框架结构和金属阻尼器的模拟方法以及相应的参数取值,图4为附加金属阻尼器的框架结构有限元模型以及边界条件。以下在进行参数分析时,以此模型为对照组模型,金属阻尼器的取值如表3所示。
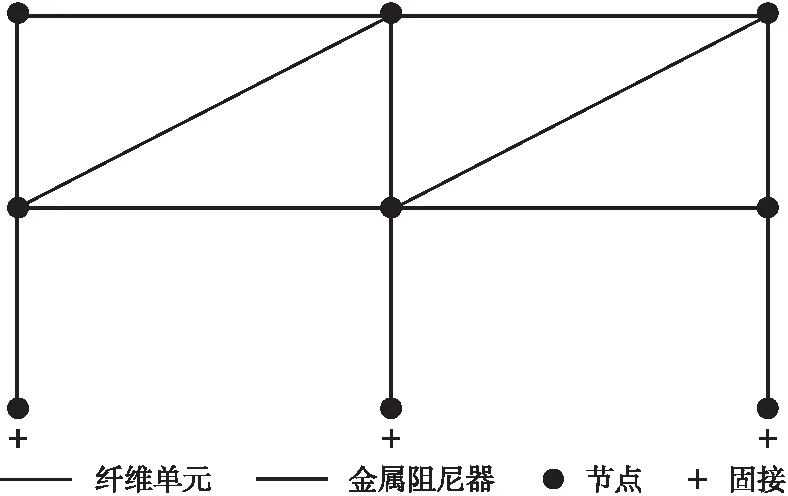
图4 有限元模型

表3 金属阻尼器参数取值Fy/kNE0/(kN·mm-1)ba1a2a3a410 100 0.020.2550.755
3 不同参数对框架结构抗震性能的影响
3.1 金属阻尼器布置方式的影响
阻尼器的布置方式对于框架结构的抗震性能具有一定的影响[5],因此本文分成以下3种情况来进行研究(见图5、图6),分别取模型编号为JF1、JF2、JF3。
由图6a的滞回曲线可知,JF1模型的承载力为81.80 kN,JF2和JF3模型的承载力一致,为90.55 kN,造成第1种布置方式承载力不足的原因主要是整体结构采用的是不对称形式,而第2种和第3种布置方式则是对称的,在往复荷载作用下,更有利于结构受力。由图6b骨架曲线可知,模型JF1屈服位移为82.547 mm,模型JF2和JF3的屈服位移为90.125 mm,可以得出,对称布置阻尼器更有利于提高框架结构的屈服位移。
本文采用等效粘滞阻尼系数来评估结构的耗能能力,图6c为3个模型中等效粘滞阻尼系数随顶点位移的变化关系,由图可知3个模型的等效粘滞阻尼系数随顶点位移增加呈增大趋势,模型JF1在其主要阶段的等效粘滞阻尼系数均大于相同位移下的JF2和JF3,模型JF1最大等效粘滞阻尼系数为3.59、模型JF1和JF2最大等效粘滞阻尼系数分别为0.44、0.43。图6d为3个模型的刚度退化曲线,本文采用割线刚度描述结构在往复荷载作用下的刚度退化情况,由图可知,3个模型在初期刚度退化较快,随着位移增加,试件刚度退化逐渐变缓。JF1刚度退化稍快于模型JF2和JF3,模型JF2和JF3刚度退化规律一致。
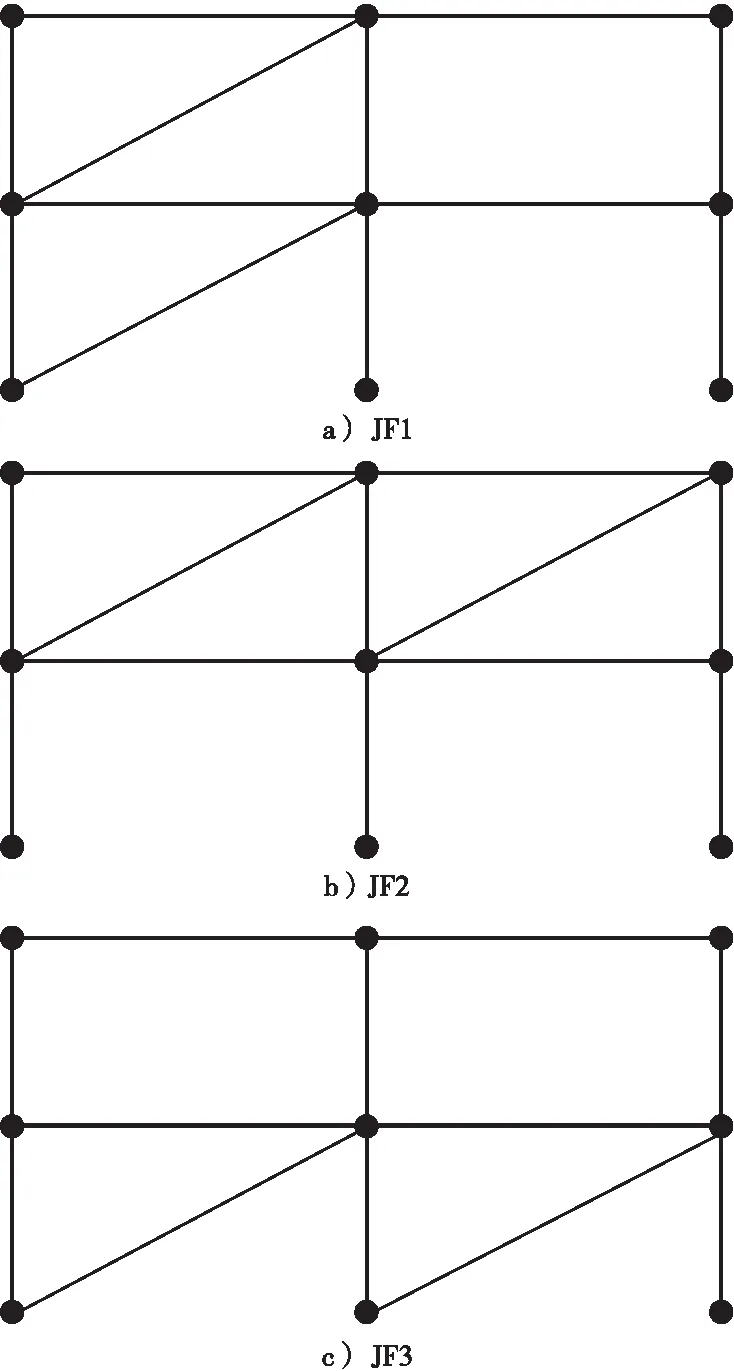
图5 不同金属阻尼器布置方式
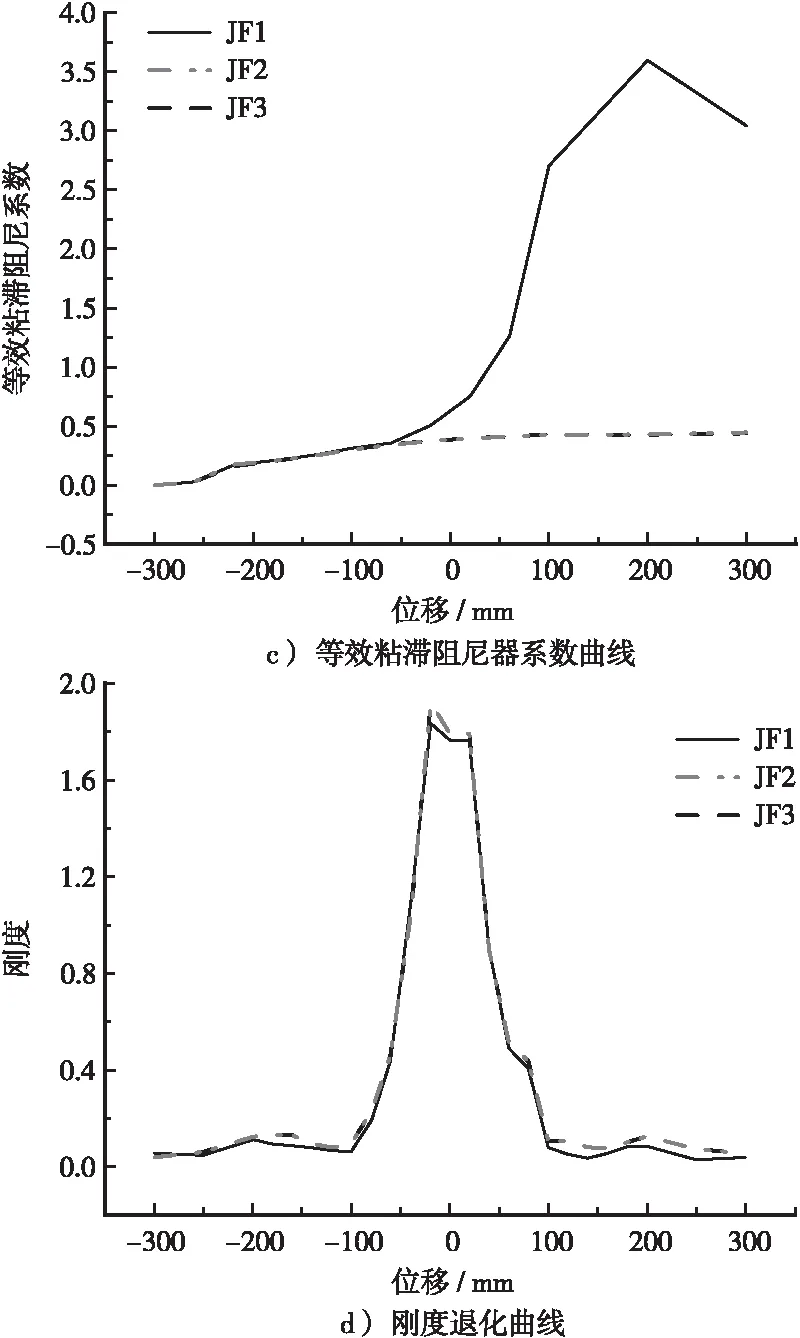
图6 不同布置方式滞回性能分析
3.2 金属阻尼器弹性模量的影响
在附加金属阻尼器的框架结构设计中,金属阻尼器的参数取值对结构抗震性能有一定影响。因此,本文取弹性模量分别为50 、100 、200 kN/mm的附加阻尼器框架结构进行往复荷载作用,研究结构的滞回性能(见表4、图7)。
由图7a滞回曲线可知,JF-E0、JF-E02、JF-E03模型的承载力分别为88.40、90.55、97.384 kN,可以明显看出随着弹性模量增大,结构承载力随之提高;随着金属阻尼器弹性模量增加,结构滞回环面积有一定增加。由图7b骨架曲线可知,JF-E01、JF-E02、JF-E03模型的屈服位移分别为84.257、90.125、92.687 mm,金属阻尼器弹性模量的增加会适当提高框架结构的屈服位移。

表4 金属阻尼器的弹性模量取值kN·mm模型JF-E01JF-E02JF-E03弹性模量50 100200
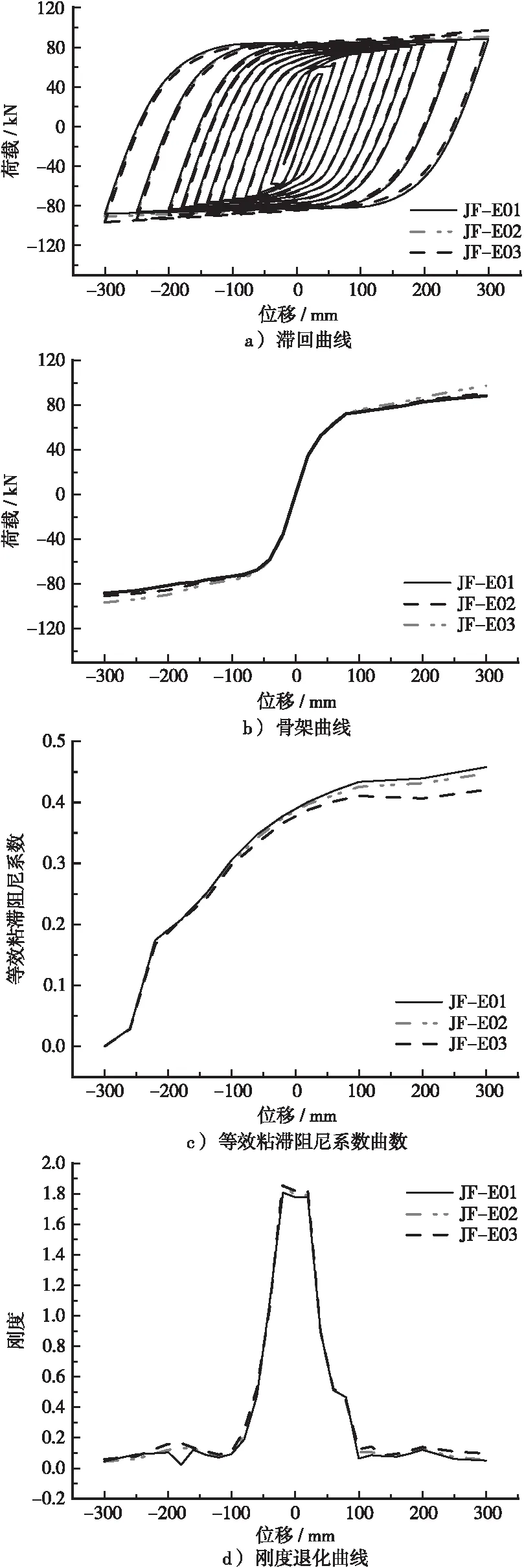
图7 不同参数的框架结构滞回性能分析
图7c为3个模型中等效粘滞阻尼系数随顶点位移的变化关系,由图可知3个模型的等效粘滞阻尼系数随顶点位移增加呈增大趋势,3个模型最大等效粘滞阻尼系数分别为0.46、0.45、0.42。随着金属阻尼器弹性模量增加,结构的等效粘滞阻尼系数越小,结构的耗能能力越差。图6d为3个模型的刚度退化曲线,由图可知,3个模型在初期刚度退化较快,随着位移增加,试件刚度退化逐渐变缓,3个模型的刚度退化规律基本一致。
4 结论
在提高框架结构抗震性能中,金属阻尼器的布置方式和参数取值是建设过程中的重点和难点。通过利用OpenSees建立附加金属阻尼器的有限元简化模型以及有限元分析,可以得到以下结论:
1) 由金属阻尼器不同布置方式的滞回性能可知,对称布置的金属阻尼器相比于不对称布置,结构的承载力更高、屈服位移更大、受力性能更好,但竖向不对称布置的结构耗能能力更强。
2) 随着金属阻尼器弹性模量增加,结构的承载力、屈服位移以及等效粘滞系都有一定提高。说明阻尼的弹性模量越大,结构的抗震性能,耗能效果越好,但刚度退化规律基本一致。

